Herzlich willkommen in der Welt der magischen Quadrate.
Das Programm wird mit dem „Inhaltsverzeichnis“ gestartet. Von dort können alle Dateien des Programms “Hexen 1x1” aufgerufen werden.
Wichtiger Hinweis!
Die im Inhaltsverzeichnis aufgeführten und im Text beschriebenen Excel-Dateien und – Programme können nicht im Internet geöffnet und angewendet werden.
Das „Hexen 1x1“ einschließlich aller Excel-Dateien und – Programme kann unter www.magquadra.de aufgerufen und als komplettes PC-Programm geöffnet und heruntergeladen werden.
Die Nutzung setzt die Installation von „Word“ und „Excel“ auf dem Computer voraus.
Inhalt
1.2. Kleine Schule (Für Anfänger gedacht) 12
1.3. Erläuterung ausgewählter Begriffe 19
2 Bildung magischer Quadrate 25
2.1 Bildung magischer Quadrate - Einführung 25
3.1.1. Analyse des Lo - Shu - Quadrates 28
4.1 Methoden zur Bildung von Kombiquadraten 74
6.1.1 Einführung in das “Hexen 1 x 1” 107
6.2. Quadrate der 3. Ordnung 132
6.2.1. Analyse des Lo-Shu-Quadrates (Das Unveränderliche) 132
6.2.2. Das kleine Hexen 1x1 mit dem Miniquadrat 136
6.2.3. Hohe Schule des Hexen 1x1 140
6.3. Quadrate der 4. Ordnung 145
6.3.2. Das kleine Hexen 1x1 150
6.3.4. Das Hexenquadrat * Eine 3-fach-Vorgabe 168
6.3.5. Die glorreichen 4 (4-fach-Vorgaben) im Zentrum 177
6.3.7. Das Tauschquadrat * * 200
6.3.9. Primzahlen-Duos * * (Die Einmaligen) 219
6.4. Quadrate der 5. Ordnung 230
6.4.2. Die “Hohe Schule” des Hexen 1x1 236
6.4.4. Das 5er Königsquadrat * * (Ein Experiment der hohen Schule) 246
6.4.5. 5er Primzahlenquadrate * 253
6.4.6. Vorgabe einer Primzahl * * (Ein Experiment der ”Hohen Schule”) 271
6.4.7. Das rationelle 5er Quadrat 279
6.5. Quadrat der 6. Ordnung 284
6.5.1. Der Sechser im Hexen 1x1 * * 284
6.6. Quadrate der 7. Ordnung 300
6.6.4. Mehrfach-Vorgaben * * 316
6.6.5. Einfach Clever * * (ein Experiment der “Hohe Schule”) 321
6.6.6. Das 7er Königsquadrat * * (Ein Experiment der hohen Schule) 335
6.6.7. Das rationelle 7er Quadrat 338
6.7. Quadrate der 8. Ordnung 340
6.7.2. Ein gesprungenes Quadrat der 8. Ordnung * * 353
6.8. Quadrat der 9. Ordnung 373
6.8.1. Das rationelle 9er Quadrat 373
6.9.1. Und 10 ist keins * * 384
6.9.3. Rechnen mit Positionsblöcken 401
6.9.4. Zum System “Einfach Clever” 407
6.9.5. Das Supereinfache (für Anfänger) 408
7.1.1. Das Kontrollquadrat 422
7.1.2. Speziell für Fans - der Lösungsweg (Für die Berechnungen im “Kontrollquadrat”) 425
7.2.1. Berechnung von Pendelquadraten 436
7.2.2. Pendelquadrate (Excel) 439
7.3.1. Korrekturquadrate mit dem PC 440
7.3.2. Lösung - Erläuterung für Fans 445
7.3.3. Korrekturquadrate (Excel) 456
7.4.1. Erläuterungen zur Bildung von Wechselquadraten 458
7.4.2. Wechselquadrate (Excel) 460
7.6.1. Erläuterungen zu den Multiquadraten 461
7.5.2. Multiquadrate (Excel) 464
7.6.1. Erläuterungen zum Multiwürfel 465
7.6.2. Multiwürfel (Excel) 470
9.1. Quadratparade (Excel) 473
9.1.1. Ausgewählte Quadratkombinationen und andere Kuriositäten 473
9.2.2. Ausgewählte Kombiquadrate (Excel) 478
9.4.1. Primzahlen-Rahmenquadrat der 32. Ordnung (Ausschnitt) 482
9.4.2. Primzahlen Rahmenquadrat (Excel) 483
9.4.3. Das Primzahlen-Rahmenquadrat der 32. Ordnung 483
9.5. Perfektes Spiegelquadrat 488
9.6. Der halbmagische Primzahlen-Würfel der 3. Ordnung 488
1 Vorspann
1.1. Vorwort
Sicherlich kennen Sie Mag Quadra noch nicht. Er ging im Jahre 2001 aus dem Magischen Quadrat hervor und ist das Pseudonym für alle, die direkt oder indirekt zum Wissen über die magischen Quadrate beigetragen haben. Das Pseudonym Mag Quadra steht aber auch für mich, für die von mir erbrachten Lösungen, Neu- und Weiterentwicklungen, von denen ich allerdings nicht weiß, ob sie nicht schon vor mir erdacht wurden.
Recherchen im Internet, die ich nach dem Erwerb eines internetfähigen Computers Anfang 2005 durchführte, haben keinen wesentlichen Einfluss auf meine Ausführungen, bis auf einige wenige Begriffe, die ich zum besseren Verständnis übernommen habe.
Der Überwiegende Teil meiner Ausführungen beruhen auf autodidaktischen Erkenntnissen die ich mir eigenständig erarbeitet habe. Zum Anfang kannte ich nur die folgenden magischen Quadrate, die ich im Buch “Schlag nach - Natur” des VEB Bibliographischen Instituts, Ausgabe 1952, gefunden hatte.
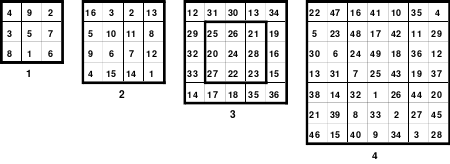
Zu diesen Quadraten wurden folgende Aussagen getroffen (außer Kursives):
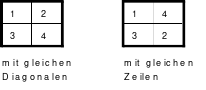
Zu 1: Ältestes magisches Quadrat aus einer chinesischen Handschrift.
(Später erfuhr Mag, dass es das “Lo-Shu-Quadrat” ist. Bis dahin nannte er es “Miniquadrat”. Im Internet sind weitere zum Lo-Shu-Quadrat zu finden.)
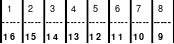
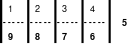
Zu 2: Dürers 16-zelliges Quadrat auf dem Kupferstich “Melancholie”, entstanden 1514, (Jahreszahl in der untersten Reihe)
Zu 3: Doppelt magisches Quadrat (Auch Rahmen- oder Schachtelquadrat genannt.)
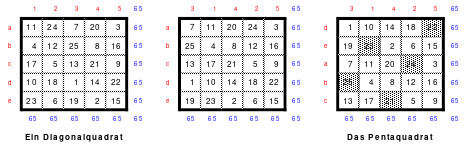
Zu 4: 49-zelliges Quadrat (Ein Diagonalquadrat, denn alle Zahlen der 7 Blöcke sind in einer Haupt- oder gebrochenen fallenden Diagonalen zu finden)
Des Weiteren ist ein halbmagisches Quadrat der 6 Ordnung dargestellt, dessen Bedeutung Mag erst später erkannte. Es kommt im Rechenexperiment “Das Superhirn” zum Einsatz.
Heute haften den magischen Quadraten nichts magisches mehr an. Nur der Name ist geblieben. Aber die Kunst des Rechnens mit magischen Quadraten ist auch heute für viele eine unerklärliche Sache. Doch deswegen hat Mag seine Ausführungen nicht als Hexen 1x1 benannt, sondern weil er diese Bezeichnung lustig findet.
Die Kenntnis der oft schwierigen Berechnungen ist für eine erfolgreiche Nutzung der Excel-Dateien nicht erforderlich. Sie wurden deshalb in der Regel ausgeblendet. Da sich aber mancher Fan auch für den Lösungsweg interessieren könnte, hat Mag diesen am Ende der Erläuterungen unter “Speziell für Fans ....” festgehalten.
Aus Sicherheitsgründen sind alle Dateien schreibgeschützt. Dieser Schreibschutz sollte nicht ohne zwingenden Grund aufgehoben werden.
Einen großen Teil dieser Ausführungen hat Mag bereits vor mehreren Jahren erarbeitet, zu der Zeit, als die Anwendersoftware “Works” gängig war. Auch wenn Mag sich bemüht hat, die Anpassung an die Standardsoftware “Excel” und “Word” möglichst fehlerfrei vorzunehmen, kann es zu fehlerhaften Bezeichnungen, auch in den Formeln, kommen. Auch war es nicht immer möglich eine Anpassung an gewünschte Formatierungen vorzunehmen ohne den Inhalt zu gefährden. Des Weiteren kommt es zur Wiederholung von Textteilen. In den meisten Fällen wurden solche herausgenommen, oder belassen, wenn eine Wiederholung als sinnvoll galt.
Die magischen Quadrate als Hexerei zu bezeichnen ist vermutlich in Zeiten entstanden, wo die mathematische Bildung nur wenigen vorbehalten war und die meisten Menschen aus Unverständnis magische Quadrate als Hexerei ansahen. Es war Ihnen geheimnisvoll, eben magisch. Die Bezeichnung “Hexeneinmaleins” findet sich in J. W. v. Goethes “Faust”, wo er die Hexe in der Hexenküche das Hexeneinmaleins aufsagen lässt. Es handelt sich dabei vermutlich um die Interpretation eines magischen Quadrates das Goethe erstellt hat, denn es war bekannt, dass sich Goethe mit magischen Quadraten beschäftigt hat. Diese Annahme wird bekräftigt durch die Analyse des Mathematikers Helmut Kracke (1900-1986), der das Hexeneinmaleins als Beschreibung eines semimagischen (halbmagischen) Quadrates auslegte und dessen Ergebnis Mag zur Grundlage seiner Aussage macht.
J. W. v. Goethes Hexeneinmaleins (blaue Schrift ist ergänzende Erklärung von Mag)
Du musst verstehen! - Aus eins mach Zehn, (durch Addition mit der 9. Siehe Quadrat 3) - Und zwei lass gehen (in Ruhe lassen) - und drei mach gleich, (drei ist gleich drei) - So bist Du reich. - Verlier die Vier! (Was verloren geht ist nicht mehr da, also Null, und fällt nach unten in die leere Zelle, in der die 9 war. Siehe Quadrat 4) - Aus Fünf und Sechs, - So sagt die Hex, - Mach Sieben und Acht, - So ist vollbracht, (Das Quadrat ist fertig! Das Quadrat 5) - Und neun ist Eins, (Die 9 ist in der 1, wodurch die 1 zur 10 wird. - Eine Erklärung wo die 9 geblieben ist!) - Und Zehn ist keins, (Die 10 ist im Quadrat 2 nicht zu finden) - Das ist das Hexen-Einmaleins!
Das Gebiet der magischen Quadrate ist sehr umfangreich. So gibt es auch magische Quadrate mit Zahlen der 2 und 3 Potenz, Primzahlenquadrate, aber auch Kurioses, wie magische Quadrate mit Wörtern, magisches 6-Eck, magische Sterne bis hin zu den magischen Würfeln. Neben der unterschiedlichen Größe gibt es auch mehrere Verfahren zur Bildung der magischen Quadrate. Mag hat der konstruktiven Bildung magischer Quadrate den Vorzug gegeben. Die Mathematik spielt nur insoweit eine Rolle, wie unter anderem auch empirische Formeln aus den konstruktiv erstellten Quadraten abgeleitet werden konnten. Die Anforderungen beschränken sich im Wesentlichen auf die 4 Grundrechenarten. Damit will Mag erreichen, dass sich auch die, die nicht über eine umfassende Ausbildung in der Mathematik verfügen, mit diesem interessanten Gebiet beschäftigen können. Wer tiefer in die mathematischen Betrachtungen zu den magischen Quadraten einsteigen möchte, der findet im Internet entsprechende Anregungen.
Die Bildung der Quadrate erfolgte stets unter dem Gesichtspunkt, eine optimale Eignung für die Anwendung im Hexen 1x1 zu erreichen. Das führte zum Teil dazu, dass die Quadrate umgestaltet wurden, was für Neulinge auf diesem Gebiet nicht immer nachvollziehbar ist. Die verschiedenen Varianten der Quadratgestaltung können schnell eine Übersicht erschweren. Um den weniger Kundigen einen Anreiz durch Erfolge zu verschaffen und Neulinge für die magischen Quadrate zu interessieren, hat Mag im Abschnitt “Kleine Schule” drei einfache Methoden beschrieben mit denen fast alle Quadratgrößen gebildet werden können. Die dabei entstehenden Quadrate sind zwar magisch haben aber meist keine weiteren Qualitätsmerkmale.
Schwerpunkt dieser Ausführungen ist die Rechenkunst mit magischen Quadraten. Das setzt allerdings auch einige Kenntnisse in der Bildung von magischen Quadraten voraus. Mag beschränkt sich hier auf wenige Varianten.
In einigen Fällen wurden meist empirische Formeln zur Bildung der magischen Quadrate gefunden, die eine Anwendung in Excel-Dateien ermöglichten. Das ist insbesondere das “Kontrollquadrat”, mit den Quadraten bis zur Größe von 20 x 20 Zellen geprüft werden können, ob diese magisch und evtl. auch pandiagonal sind. Des Weiteren die Datei “Pendelquadrate”, mit der gerade und pendelfähige Quadrate vervielfältigt werden können, wobei alle die gleiche magische Summe haben und so zu größeren Quadraten zusammengesetzt werden können und die Datei “Korrekturquadrate”, mit der wie bei den Pendelquadraten gleiche Quadrate aus ungeraden Quadraten gebildet werden können, sowie weitere Anwendungen.
Heute haften den magischen Quadraten nichts magisches mehr an. Nur der Name ist geblieben. Aber die Kunst des Rechnens mit magischen Quadraten ist auch heute für viele eine unerklärliche Sache. Doch deswegen hat Mag seine Ausführungen nicht als Hexen 1x1 benannt, sondern weil er diese Bezeichnung lustig findet.
Die Kenntnis der oft schwierigen Berechnungen ist für eine erfolgreiche Nutzung der Excel-Dateien nicht erforderlich. Sie wurden deshalb in der Regel ausgeblendet. Da sich aber mancher Fan auch für den Lösungsweg interessieren könnte, hat Mag diesen am Ende der Erläuterungen unter “Speziell für Fans ....” festgehalten.
Aus Sicherheitsgründen sind alle Dateien schreibgeschützt. Dieser Schreibschutz sollte nicht ohne zwingenden Grund aufgehoben werden.
Einen großen Teil dieser Ausführungen hat Mag bereits vor mehreren Jahren erarbeitet, zu der Zeit, als die Anwendersoftware “Works” gängig war. Auch wenn Mag sich bemüht hat, die Anpassung an die Standardsoftware “Excel” und “Word” möglichst fehlerfrei vorzunehmen, kann es zu fehlerhaften Bezeichnungen, auch in den Formeln, kommen. Auch war es nicht immer möglich eine Anpassung an gewünschte Formatierungen vorzunehmen ohne den Inhalt zu gefährden. Des Weiteren kommt es zur Wiederholung von Textteilen. In den meisten Fällen wurden solche herausgenommen, oder belassen, wenn eine Wiederholung als sinnvoll galt.
Aus gesundheitlichen Gründen hat Mag den Schriftgrad 12 gewählt. Nicht immer hat er frühere Darlegungen mit Schriftgrad 10 umgearbeitet.
Mag wünscht Ihnen bei der Lektüre seiner Ausführungen und der Anwendung der Excel-Programme viel Spaß. Mögen Sie Ihr Interesse finden und Ihre Kenntnisse über die magischen Quadrate vertiefen.
Sicherheit
Zum Schutz der Dateien sind diese schreibgeschützt, auch die Excel-Dateien. Der Schreibschutz sollte nicht ohne zwingenden Grund aufgehoben werden. Die Excel-Dateien können trotz des Schreibschutzes einwandfrei genutzt werden. Werden diese geschlossen, so ist die Frage „Sollen die Veränderungen gespeichert werden“ mit „Nein“ zu beantworten. Mit dieser Entscheidung wird die Datei in seinen Originalzustand nicht verändert. Eventuell anders lautende Erklärungen in den einzelnen Abschnitten sind sekundär zu betrachten.
Urheberrechte
Mag erhebt urheberrechtliche Ansprüche auf Vervielfältigung, jeglicher Art, auch teilweise, für gewerbliche Zwecke, sowie auf Veröffentlichungen. Kopien für den persönlichen Bedarf sind davon ausgenommen. Die Benutzung des Werkes für Vorträge und ähnlichen Veranstaltungen, sowie für künstlerische Auftritte gilt nicht als Veröffentlichungen und ist erlaubt. Da Mag annimmt, dass seine Darstellungen bereits bekannt sein könnten, erhebt er keine urheberrechtliche Ansprüche auf die dargestellten Quadrate.
Manfred Albrecht
Dresden 2024
magquadra@t-online.de
1.2. Kleine Schule (Für Anfänger gedacht)
In der “Kleinen Schule” werden einfache Methoden gezeigt, mit denen theoretisch magische Quadrate aller Größen erstellt werden können. Große Quadrate, größer 20. Ordnung, sollten nicht in dieser Form erstellt werden, da es einfachere Wege dazu gibt. Das sind z.B. Kombiquadrate, wo mehrere Quadrate zu größeren zusammengefügt werden. Es ist ausreichend, wenn man als Neuling auf dem Gebiet der magischen Quadrate mit kleineren Quadraten beginnt. Bei den Beschreibungen der “Bildung von magischen Quadraten und der Anwendung in der Rechenkunst” ging es vorwiegend um Quadrate mit denen ein möglichst leichtes Rechnen erreicht wird. Diese Quadrate sollten Qualitätsmerkmale wie pandiagonal, homogen, pendelbar und weitere besitzen. Das führte oft zu manipulierten Quadraten, die für Anfänger nicht immer nachvollziehbar sind. Ziel der “Kleinen Schule” ist es, Neulingen erste Erfolgserlebnisse zu ermöglichen und vor allem ein Interesse an den magischen Quadraten zu wecken.
Quadrate, die mittels der nachfolgend beschriebenen Methoden erstellt werden, sind in der Regel nur magisch. Andere Merkmale sind nicht zu erreichen und wenn welche möglich sind, wird darauf nicht eingegangen.
Quadrate ungerader Ordnungszahlen
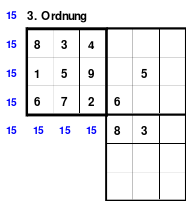
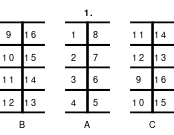
Alle ungeraden Zahlen können nicht durch 2 geteilt werden und machen 50% aller Zahlen aus. Das kleinste ist das Quadrat der 3. Ordnung (links). Es kann mittels der Springermethode gebildet werden. Die Sprünge sind innerhalb der Blöcke 2 Zellen nach rechts und eine nach unten. Die Größe und Anzahl der Blöcke entsprechen der Ordnungszahl. Beim Quadrat der 3. Ordnung sind das 3 Blöcke mit jeweils 3 Zahlen, das ist Block 1 mit den Zahlen 1; 2; 3, dem 2. Block mit 4: 5: 6 und dem 3. Block mit den Zahlen 7; 8 und 9. Die Sprünge sind in der Abbildung gut zu erkennen, wozu 2 weitere Quadrate angehängt wurden. Dabei wird eine wichtige Regel erkannt. Gelangt man an die rechte Begrenzung, wird einfach von links aus weiter gezählt. Gleiches trifft zu beim Erreichen der unteren Quadratbegrenzung. Hier wird einfach von oben weiter gezählt.
Eine weitere Regel sind die Übergänge von Block zu Block. Dieser ist eine Zelle nach rechts. Siehe 3 zu 4; 6 zu 7 und 9 zu 1. Am Übergang von 9 zum Anfang 1 ist auch zu erkennen, dass alle Zahlen eine Schleife bilden. Die letzte zu beachtende Regel ist, die 1 befindet sich in der mittleren Zelle der ersten Spalte. Mit diesem Wissen wurden die nachfolgenden Quadrate der 5.; 7. und auch der 9. Ordnung aufgebaut.
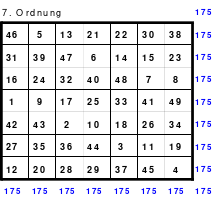
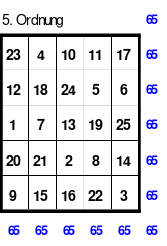
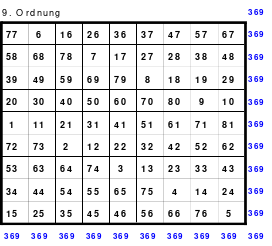
Quadrate mit einer geraden Ordnungszahl
Bis auf das Quadrat der 4. Ordnung können alle geraden Quadrate mittels der Fusionsmethode gebildet werden, Das 4er kann jedoch in einer nur leicht abgewandelten Variante dieser Methode erstellt werden. Da die Fusionsmethode etwas komplizierter ist, wird die leichter zu handhabende Wendemethode erläutert. Die Qualität dieser Quadrate ist jedoch geringer gegenüber den Quadraten, die nach der Fusionsmethode erstellt werden. Die Wendemethode kann für die mehrfach geraden Quadrate ohne Probleme eingesetzt werden. Diese enthalten mindestens 2mal die 2 im Produkt, z.B. 4 (2*2); 8 (2*2*2) oder 12 (2*2*3).
Die Wendemethode kann für einfach gerade Quadrate nur bedingt angewendet werden. Der Hauptgrund ist, dass z.B. bei einem 6er Quadrat jeweils 3 Spalten und Zeilen gewendet werden müssten, die aber nicht zu gleichen Teilen symmetrisch zu den Achsen eingeordnet werden können. Einfach gerade Zahlen enthalten nur 1mal die 2 im Produkt. Das trifft z.B. auf das 6er (2*3) und 10er (2*5) Quadrat zu. Die Wendemethode kann bei den einfach geraden Quadraten nur in einer veränderten Form als alternative Wendemethode genutzt werden. Diese ist aber eine regelrechte Puzzlearbeit und kann einem Neuling nicht zugemutet werden. Mag hat sich deshalb entschieden, die Fusionsmethode mit in die “Kleine Schule” aufzunehmen, damit auch für die Bildung einfach gerade Quadrate eine Lösung angeboten wird.
Die Wendemethode
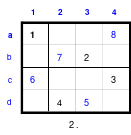
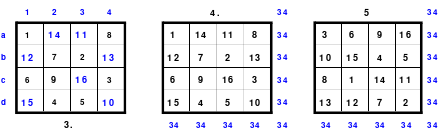
Die Wendemethode wird anhand eines Quadrates der 4. Ordnung erklärt. Ausgang ist ein Folgequadrat, in das die Zahlen in ihrer natürlichen Reihenfolge eingetragen werden (linkes Quadrat). Außer den beiden Diagonalen haben alle Reihen nicht die magische Summe von 34. Allerdings ist die Summe der mittleren, wie auch die äußeren Zeilen und Spalten, 2*34=68 groß. Um einen Ausgleich zu schaffen brauchen nur 2 Zeilen oder 2 Spalten gewendet werden, was die Hälfte der Zeilen und der Spalten ist. Diese müssen aber immer symmetrisch zu der senkrechten bzw. waagerechten Achse sein. Es können die beiden inneren Reihen oder auch die beiden äußeren Reihen gewendet werden. Andere Kombinationen führen zu falschen Summen der Diagonalen! Im Beispiel wurden die inneren Reihen zur Wende gewählt. Werden die beiden inneren Zeilen um die senkrechte Achse (Quadrat 2) gewendet, so entsteht das Quadrat 3, bei dem alle Spalten die richtige Summe 34 haben.
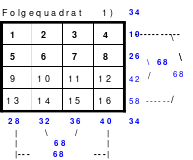
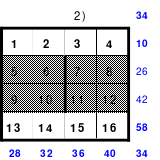
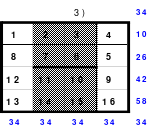
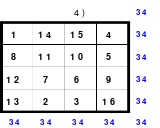
Nach dem Wenden der mittleren Spalten um die waagerechte Achse ist das Quadrat 4 fertig.
Das so entstandene Quadrat ist magisch. Es ist nicht nur dem Dürerquadrat ähnlich, sondern es ist das Dürerquadrat. Das Dürerquadrat entsteht durch das Wenden des Quadrates um seine senkrechte Achse und Austausch der oberen mit der unteren Zeile
Ein Quadrat der 8. Ordnung
Mittels der Wendemethode wurde das nachfolgende magische Quadrat der 8. Ordnung gebildet. Das Quadrat 1 ist das Folgequadrat mit den Zahlen von 1 bis 64. Die für die Wendung um die waagerechte Achse vorgesehenen 4 Spalten wurden blau markiert. Das Quadrat 2 zeigt die erfolgte Wendung und die für die Wende um die senkrechte Achse vorgesehenen Spalten grün markiert. Das Quadrat 3 ist das fertige magische Quadrat. Alle Zeilen, Spalten und die beiden Diagonalen haben die Summen von 260.
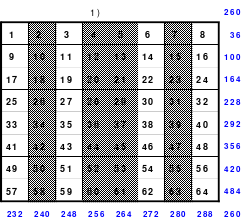
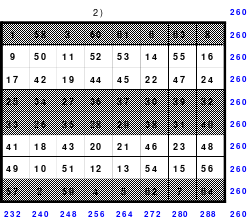
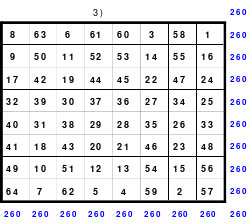
Die Fusionsmethode
Die Fusionsmethode ist eine erweiterte Wendemethode und gehört normalerweise nicht in die “Kleine Schule”. Sie ist eine Stufe höher einzuordnen. Wenn Mag sie trotzdem in die “Kleine Schule” aufgenommen hat, so aus mehreren Gründen:
Die alternative Wendemethode für einfach gerade Quadrate erweist sich als ein regelrechtes Puzzlespiel.
Das Zahlenbild ist bei Quadraten der Wendemethode nicht attraktiv.
Die Zahlen sind nicht gut verteilt, z. B. sind in der 1. Zeile nur kleine und große Zahlen enthalten.
Im Abschnitt “3.2.3. Fusionsmethode” steht die Anwendung mit dem Ziel, eine wenigstens Teilhomogenität zu erreichen, im Vordergrund.
Die Grundlösung wird dabei nicht ausreichend erläutert.
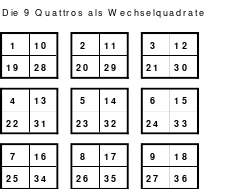
Bei der Fusionsmethode kommen Quattros zum Einsatz. Das sind 2 mal 2 große Quadrate, die natürlich nicht magisch sein können. Für das 6er Quadrat sind 9 Quattros erforderlich, die nach der Wechselmethode mit Zahlen versehen werden. Bei der Wechselmethode werden die Zahlen 1 bis 9 in die Zellen 1 eingesetzt. Die nächsten Zahlen, die 10 bis 18 kommen in die Zellen 2 usw. Die 2 Diagonalen in den Quattros sind gleich groß, was ein Wenden zulässt. Das hat Bedeutung für die Quattros, die in die Diagonalen eingeordnet werden. Die so entstandenen Quattros werden in das Miniquadrat eingesetzt. (Siehe Quadrat 1).
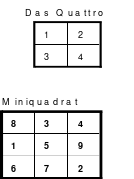
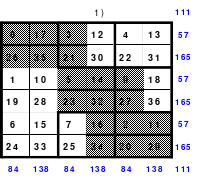
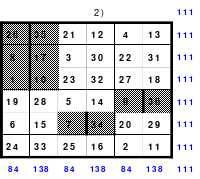
Das entstandene Quadrat ist nicht magisch. Nur die Diagonalen haben die richtige Summe mit 111. Die Zeilen haben im Wechsel die Summen 57 und 165. Die Differenz ist 108, wovon je die Hälfte, das ist 54, den Zeilensummen zugeschlagen bzw. abgezogen werden muss, um die richtige Summe 111 zu erhalten. Alle Zahlenpaare dieser Zeilen haben eine Differenz von 18 und 3*18 ist 54. Folglich müssen 3 Zahlenpaare, das ist die Hälfte der Ordnungszahl 6, gewendet werden, um einen Ausgleich herzustellen. Dabei gilt, dass die Quattros auf den Diagonalen insgesamt zu wenden sind. Wird nur ein Zahlenpaar gewendet, wird die Diagonale verändert und damit die Diagonale des Gesamtquadrates, die dann nicht mehr den Wert 111 hat. Quadrat 1 zeigt eine mögliche Festlegung. Nach erfolgter Wendung ist das Quadrat 2 entstanden. Alle Zeilen haben 111 als die richtige Summe.
Die Spalten haben paarweise 84 und 138 als Summe. Hier ist die Differenz 54. Um die Summe 111 zu erhalten müssen auch hier 3 Zahlenpaare gewendet werden. Denn die Differenz der Zahlenpaare der Spalten beträgt einheitlich 9 und 9*3 ist 27, die Hälfte der Spaltendifferenz. In den linken beiden Spalten haben alle Zahlenpaare die Differenz 9. Gewählt wurden die oberen 3 (grüne Markierung). In den beiden anderen Spaltenpaaren ist das nicht möglich. Hier haben nur die Quattros, die entweder gewendet oder nicht gewendet wurden die Differenz von 9 und wenn, dann stimmt oft das Vorzeichen nicht. Hier sind aber Zahlenpaare zu finden, die eine Differenz von 27 haben und damit allein die Zeilendifferenz ausgleichen. (gelbe und blaue Markierung im Quadrat 2). Das ist kein Zufall, sondern mathematisch bedingt. Im Quadrat 1 sind die Quattros 3, 7 und 9 rot umrahmt. Bei der Richtigstellung der Zeilensummen wurden in diesem Quattros nur ein Zahlenpaar gewendet, wodurch die kleinste und größte Zahl zu einem waagerechten Zahlenpaar mit der Differenz von 27 entstand. Nach erfolgter Wendung ist das Quadrat 3 fertig. Es ist magisch, aber weder pandiagonal oder homogen.
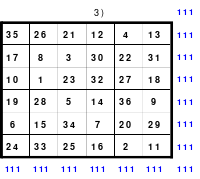
Nach dieser Methode können auch die weiteren einfach geraden Quadrate wie das der 10.(2*5) und 14. (2*7) Ordnung erstellt werden, wobei diese aufgrund der zunehmenden Größe leichter zu bilden sind.
Noch einfacher können die mehrfach geraden Quadrate, wie das der 8.Ordnung, gebildet werden, weil hier die Möglichkeit gegeben ist, immer komplette Quattros zu wenden.
Mag schließt die “Kleine Schule” mit der Hoffnung, dass Sie Interesse an den magischen Quadraten gefunden haben.
1.3. Erläuterung ausgewählter Begriffe
Um die Beschreibungen einfach und verständlich zu gestalten, ist es notwendig einige Begriffe, die mehrfach benutzt werden zu erläutern. So werden lange Erklärungen in den einzelnen Abschnitten vermieden. Es ist nicht beabsichtigt all die vielen Begriffe die bei den magischen Quadraten Verwendung finden zu erläutern. Mag beschränkt sich auf die von Ihm in diesen Ausführungen verwendeten. Dabei kann es sein, dass in der Literatur zu diesem Komplex andere Begriffe verwendet werden. Mag hat sich von den Abweichungen selbst überzeugen können, als er Anfang 2005 mit einem neuen Computer im Internet recherchierte. Da zu diesem Zeitpunkt das beabsichtigte Buch bereits fast fertig gestellt war, hat er es bei seinen Bezeichnungen belassen. Lediglich einige, wenige Begriffe hat er übernommen, da diese die besseren waren. Ich will für die Fans der magischen Quadrate keine Eulen nach Athen tragen, aber er weiß andererseits nicht, welche Kenntnisse ein Neuling auf diesem Gebiet hat.
Magisches Quadrat
Ein magisches Quadrat setzt sich aus einzelnen Zellen zusammen. Dabei ist die Anzahl der Zellen in den Zeilen genauso groß wie in den Spalten, z.B. 3x3=9 Zellen, oder 7x7= 49 Zellen. In ein solches Quadrat sind die Zahlen von 1 bis n lückenlos so einzuordnen, dass die Summen der Zahlen in den Zeilen, den Spalten und in den Diagonalen gleich groß sind.
Basisquadrat
Das magische Quadrat mit den Zahlen 1 bis n bezeichnet Mag als Basisquadrat (teilweise auch als Grundquadrat). Auf dieses wird im Hexen 1 x 1 immer wieder Bezug genommen.
Semimagische Quadrate
Das sind magische Quadrate bei denen nicht alle Reihen, meistens die Diagonalen, als Summe die magische Summe haben. Diese Quadrate werden auch halbmagische oder teilmagische Quadrate genannt.
Ordnung der Quadrate
Die Quadrate werden nach ihrer Größe bezeichnet. So wird ein 9 x 9 großes Quadrat als Quadrat der „9. Ordnung“ oder kurz als „9er Quadrat“ bezeichnet.
Magische Summe (MS)
Die Summen der waagerechten, senkrechten und diagonalen Reihen eines magischen Quadrates müssen gleich sein. Sie werden als die magische Summe des Quadrates bezeichnet. Die magische Summe des Basisquadrates berechnet sich aus:
(1 + O2) /2 * O = MS
(O ist die Ordnungszahl und O2 die größte Zahl)
Zahlenblöcke
Die Zahlen der magischen Quadrate können in der Regel in Blöcke zusammengefasst werden. Die Anzahl der Blöcke entspricht der Ordnung des Quadrates, ebenso die Anzahl der Zahlen je Block. Ein Quadrat der 5. Ordnung hat folglich 5 Blöcke mit je 5 Zahlen. Im Einzelnen 1 bis 5, 6 bis 10, 11 bis 15, 16 bis 20 und 21 bis 25.
Reihen
Die Spalten, Zeilen und die Hauptdiagonalen können unter dem Begriff Reihen zusammengefasst werden.
Zeilen
Zeilen sind die waagerechten Zahlenreihen im Quadrat.
Spalten
Spalten sind die senkrechten Zahlenreihen im Quadrat
Diagonalen
Diagonale sind die Zahlenreihen zwischen den Eckzellen. Sie werden auch als die ganzen - oder Hauptdiagonalen bezeichnet. Es wird unterschieden zwischen fallenden und steigenden Diagonalen. Dabei wird die Diagonale stets von links nach rechts betrachtet. Die fallende Diagonale ist die von oben links nach unten rechts. Die steigende die von unten links nach oben rechts. Im linken Quadrat ist die fallende Diagonale blau und die steigende gelb gekennzeichnet.
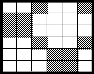
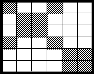
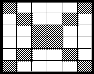
Das mittlere Quadrat zeigt eine gebrochene steigende Diagonale (rot) und eine gebrochene fallende Diagonale (grün). Durch Verschieben von Spalten und/oder Zeilen können die gebrochenen Diagonalen zu Hauptdiagonalen werden.
Pandiagonal
Pandiagonal ist ein Quadrat bei dem auch die Summen der gebrochenen Diagonalen der magischen Summe entsprechen. Dies trifft sowohl auf die fallenden, als auch auf die steigenden zu. Das ist von sehr großer Bedeutung. Denn bei pandiagonalen Quadraten können die Spalten und Reihen versetzt werden, wobei das Quadrat stets magisch bleibt.
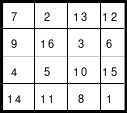
Das linke Quadrat ist ein pandiagonales mit der magischen Summe von 34. Wird z. B. die oberste Zeile nach unten versetzt, so haben sich die Summen der Spalten und Zeilen nicht verändert, denn die Zahlen verbleiben in diesen. Die Hauptdiagonalen dagegen setzen sich nach einer solchen Verschiebung aus anderen Zahlen zusammen. Bei einem pandiagonalen Quadrat wird die Summe der neuen Hauptdiagonalen der magischen Summe entsprechen, denn diese setzen sich ja aus vorher geteilten zusammen. Die Richtigkeit ist im mittleren Quadrat zu erkennen. Hier wurde die obere Zeile nach unten und anschließend die vordere Spalte nach hinten versetzt. Das Quadrat ist ein magisches geblieben. Das trifft auch auf das rechte Quadrat zu. Hier wurden die Spalten 1 und 2 nach hinten und die Zeile 1 nach unten versetzt.
Pendelbar
Ein magisches Quadrat ist pendelbar, wenn sich in jeder Spalte, Zeile und Diagonalen je eine gerade und eine ungerade Zahl befinden. Pendeln ist eine Konstruktionsmethode zur Bildung größerer Quadrate.
Es ist logisch, dass diese Forderung bei ungeraden Quadraten nicht erfüllt werden kann, weshalb ungerade Quadrate nur bedingt gependelt werden können.
Homogen
Homogen ist ein Quadrat, wenn sich in jeder Reihe je eine Zahl von jedem Block befindet. Das trifft auf alle pandiagonalen Quadrate zu und ist eine wichtige Voraussetzung um das Quadrat im Hexeneinmaleins einsetzen zu können.
Des Weiteren muss sich in jeder Reihe eine 1., 2., 3. usw. Zahl eines Blockes befinden.
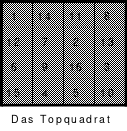
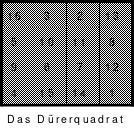
Das linke Quadrat ist ein homogenes, denn von den Blöcken 1 - 4 (blau), 5 - 8 (rot), 9 - 12 (grün) und 13 - 16 (gelb) befindet sich je eine in jeder Reihe. In der oberen Reihe befindet sich 1 als 1. Zahl des 1. Blockes, die 14 als 2. Zahl des 4. Blockes, die 11 als 2. Zahl des 2. Blockes und die 8 als 4. Zahl des 2. Blockes.
Bei dem Dürerquadrat (rechts) ist dies nicht der Fall. Die Homogenität ist beim Hexeneinmaleins, der Rechenkunst mit magischen Quadraten, von großer Bedeutung.
Teilhomogen
Bei einem teilhomogenen Quadrat müssen wenigstens die jeweils größten Zahlen in je eine Reihe enthalten sein. Dadurch kann das Quadrat zu einem Multiquadrat gebildet werden, weil dann verbleibende Restgrößen diesen Zahlen zugeschlagen werden können ohne das Zahlen mehrfach auftreten. Die Anzahl der großen Zahlen entspricht dabei der Ordnungszahl des Quadrates.
Teilhomogen ist auch ein Quadrat, bei dem die Homogenität durch Versetzen von Reihen aufgehoben wird. Ein solches ist z. B. das Topquadrat.
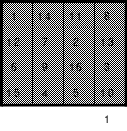
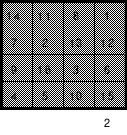
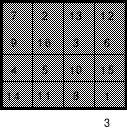
Links (1) ist das Topquadrat. Es ist homogen. Bei dem Quadrat in der Mitte (2) wurde eine Spalte, die erste, nach hinten versetzt. Es ist nicht mehr homogen, denn in den Hauptdiagonalen befinden sich 2 Zahlen aus dem 1. und 2. Zahlen aus dem 4. Block. Auch die Regel jeweils eine 1., 2., 3. und 4. aus einem Block wird nicht erfüllt.
Das rechte Quadrat (3) ist nach versetzen einer weiteren Reihe, der oberen nach unten, wieder homogen.
Die Teilhomogenität kann im Hexen 1x1 zu Problemen führen. Dazu mehr im Hexen 1x1.
Duos
Die Duos sind die gleich großen Zahlenpaare einer Duokette
Duokette
Bei der Duokette werden von einer natürlichen Zahlenkette die kleinste und die größte Zahl, die 2.-kleinste und die 2.-größte Zahl usw. zu Duos zusammengefügt. Die Duos haben im jeweils konkreten Fall gleiche Größe. Es ist zwischen geraden und ungeraden Duoketten zu unterscheiden. Bei den ungeraden Duoketten bleibt die mittlere Zahl der natürlichen Zahlenkette ohne Ergänzungszahl. Duoketten sind unverzichtbar bei der Konstruktion magischer Quadrate und im Hexen 1 x 1.
Quattros
Quattros sind 2 x 2 = 4-zellige Quadrate, die natürlich niemals magische sein können. Sie spielen aber bei der Konstruktion magischer Quadrate, u. a. nach der Fusionsmethode eine Rolle.
(Weitere Begriffe, wie Quadratsumme, assoziativ, kommutativ, Distributiv u. a. tauchen in den Beschreibungen evtl. auf, haben aber keine Bedeutung bezüglich der weiteren Ausführungen.)
2 Bildung magischer Quadrate
2.1 Bildung magischer Quadrate - Einführung
In den nachfolgenden Abschnitten wird die Bildung magischer Quadrate beschrieben. Es gibt sehr viele Methoden dazu, sowohl konstruktive als auch mathematische. Mag beschränkt sich nur auf wenige, vor allem auf leicht verständliche. Wobei den konstruktiven Methoden der Vorzug gegeben wird.
Vor allem mussten solche magischen Quadrate gefunden werden, deren Konstruktion einfach und nachvollziehbar ist, damit sie sich für die Rechenkunst im Hexen 1x1 eignen.
Auch ist es notwendig, dass Sie ausreichende Kenntnisse zur Quadratbildung haben. Denn wer sich als Rechenkünstler mit magischen Quadraten betätigt, muss über ein gewisses Maß an Kenntnissen dazu verfügen. Sonst ist er unter Umständen nicht glaubwürdig. Wer weitergehende Kenntnisse erlangen möchte, findet im Internet ausreichende Informationen.
Die nachstehenden Ausführungen werden maximal bis auf Quadrate der 20. Ordnung beschränkt. Die dabei erlangten Kenntnisse sind ausreichend, um auch größere Quadrate zu konstruieren. Des Weiteren muss bei der Bildung magischer Quadrate darauf geachtet werden, dass sie pandiagonal und homogen sind, weil diese sich besonders gut für das Hexen 1x1 eignen. Die Gründe werden in den weiteren Ausführungen noch genannt.
Bei den magischen Quadraten wird in erster Linie zwischen den geraden und den ungeraden Quadraten unterschieden. Erstere haben eine gerade Ordnungszahl und die anderen eine ungerade.
Die ungeraden Quadrate sind in der Regel am leichtesten konstruktiv zu erstellen. Das trifft insbesondere auf die Primquadrate zu. Primquadrate sind Quadrate mit einer Primzahl als Ordnungszahl. Das sind z. B. 5er, 7er, 11er, 13er, 17er und 19er Quadrate. Die Primquadrate sind nicht zu verwechseln mit Primzahlenquadraten, bei denen alle Zahlen des Quadrates Primzahlen sind. Die einfachste Methode zur Bildung der Primquadrate ist die Springermethode, die in den folgenden Abschnitten beschrieben wird. Die dabei entstehenden Quadrate sind nicht nur magisch, sondern vor allem pandiagonal und homogen, d. h. in jeder Reihe befindet sich eine Zahl eines Blockes, wovon jeweils eine 1., 2., 3 usw. Zahl, die eines Blockes ist, weshalb sie für das Hexen 1x1 sehr gut eignet sind.
Nicht so gut geeignet sind die Tri-Quadrate. Das sind z.B. die Quadrate der 9. und 15. Ordnung. Ihr Produkt besteht aus nur 2 Primzahlen, wobei die eine, eine 3 ist. Diese sind wegen ihrer Teilbarkeit durch 3 (Tri) zwar mittels der Springermethode realisierbar, jedoch nur unter Beachtung besonderer Regeln. Die Qualität reicht bei weitem nicht an die der Primquadrate heran. Nur durch Umstellungen eignen sie sich eingeschränkt für das Hexen 1x1. Mag wird sie deshalb nicht in das Hexen 1x1 aufnehmen.
Um sie aber nicht ganz auszuschließen hat Mag Voraussetzungen geschaffen die eine einfache Bildung von Triquadrate ermöglichen. Neben anderen Methoden wird das mit der Korrekturmethode erreicht, bei der durch Austausch von Blöcken eine gleiche magische Summe für die einzelnen Quadrate erzielt wird. Die Korrekturmethode ist sehr kompliziert, weshalb Mag die Excel-Datei “Korrekturquadrate” erstellt hat, mit der die Bildung gleichgroßer Primquadrate ermöglicht wird, die dann zu größeren Quadraten zusammengefügt werden können.
Die geraden magischen Quadrate unterscheiden sich in einfach und mehrfach gerade Quadrate. Die Ordnungszahlen der einfach geraden Quadrate können nur einmal durch 2 geteilt werden. Das sind die Quadrate mit den Ordnungszahlen 6, 10 und 18. Die anderen können durch 2 x 2 = 4 geteilt werden, was auf die Ordnungszahlen 4, 8, 12, 16 und 20 zutrifft. Die geraden magischen Quadrate sind nicht so leicht zu bilden wie die ungeraden. Bei den geraden ist die Fusionsmethode die geeignete. Da diese Umstellungen erfordern und das nicht nur für das Hexen 1x1, wird diese Methode nur zur Bildung der Quadrate der 6. und 10. Ordnung eingesetzt. Das Quadrat der 4. Ordnung wird unter Beachtung der erworbenen Erkenntnisse regelrecht als Puzzlequadrat erstellt. Die anderen mehrfach geraden Quadrate erhält man durch das Pendeln gerader und homogener Quadrate. Wie bei der Korrekturmethode werden kleinere Quadrate zu mehreren Quadraten vervielfältigt, die dann zu größeren Quadraten zusammengesetzt werden können. Beim pendeln pendelfähigen geraden magischen Quadraten entstehen magische Quadrate mit gleicher magischer Summe und können beliebig zusammengesetzt werden.
Auch hier hat Mag eine Excel-Datei erstellt, mit der die Bildung der “Pendelquadrate” erleichtert wird. Die Pendelmethode wird ebenfalls in den weiteren Erläuterungen beschrieben.
Das bisher Gesagte in einer Übersicht
Dazu eine kleine Zahlenkunde:
Alle Zahlen, so auch die Ordnungszahlen der magischen Quadrate, sind Produkte von Primzahlen. Unter dem Gesichtspunkt des Hexen 1x1 können diese wie folgt untergliedert werden:
3 Soloqudrate
3.1 ungerade Quadrate
3.1.1. Analyse des Lo - Shu - Quadrates
Das Lo Shu-Quadrat ist das kleinstmögliche magische Quadrat. Mag nennt es deshalb auch das Minquadrat. Es ist das älteste bekannte Quadrat, denn es wurde bereits 1200 v. Chr. dokumentiert (diese Jahreszahl wird nicht einheitlich genannt). Danach soll eine Schildkröte dem Fluss Lo entstiegen sein, auf deren Rücken das Lo Shu-Quadrat, ein 3 mal 3 = 9 Zahlen großes Quadrat, abgebildet war.
Im Internet sind viele Beiträge zum Lo Shu-Quadrat zu finden, die sich in vielfältiger Form, mathematisch, religiös, astrologisch und weiteren, mit diesem Quadrat beschäftigen.
Mag hat aber keine Beiträge über die Ableitung zu größeren magischen Quadraten und deren Einsatz in der Rechenkunst gefunden.
(Wahrscheinlich hat er nicht lange genug recherchiert?)
Mag wird nachfolgend einige Betrachtungen zum Lo Shu- Quadrat vornehmen, wobei er nur auf die Eigenschaften und Probleme eingeht, die für seine weiteren Darlegungen von Bedeutung sind. Dabei wird er sich nur auf Ergebnisse seiner Analyse beschränken und auf eine weitgehende mathematische Beweisführung verzichten.
Diese Darlegungen werden zum Teil in den weiteren Beiträgen als Grundlage wiederholt.
Lehrmeister Lo Shu
Das Lo Shu kann mit verschiedenen Methoden gebildet werden. Das bedeutet auch, dass aus dem Lo Shu durch Analyse die Methoden zur Bildung von Quadraten gefunden werden kann, was allerdings nur auf ungerade Quadrate zutrifft.
Mag hat diese Analysen in den meisten Fällen nicht am Anfang gemacht, sondern teilweise erst nach der Aneignung der Methoden über andere Wege.
Lo Shu ein Diagonalquadrat
Nach der Analyse des Miniquadrates mit nur 9 Feldern fand Mag das System, nach dem dieses gebildet wurde und dass es auch ermöglicht, beliebig große magische Quadrate mit einer ungeraden Anzahl von Feldern zu erstellen. Auf der nächsten Seite links ist das Miniquadrat abgebildet. Mag fiel auf, dass die Zahlen des mittleren Blockes 4 bis 6 die fallende Diagonale belegen. Ausgehend von der Zelle 4 befindet sich die Zelle 5 um 1 Zelle nach rechts und 1 Zelle nach unten. Auch die Zelle 6 befindet sich analog von Zelle 5. Danach betrachtete Mag die Zahlen der anderen Blöcke und fand heraus, dass auch diese genauso zueinander angeordnet sind. Geht man von der Zelle 1 eine nach rechts und eine nach unten, so kommt man auf die Zelle 2 und weiter auf Zelle 3. Auch der 3. Block mit den Zahlen 7, 8 und 9 ist in gleicher Weise geordnet.
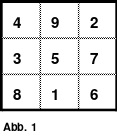
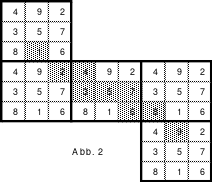
Weiter ist festzustellen, dass die 1. Zelle des folgenden Blockes stets über der letzten Zelle des vorangegangenen Blocks liegt. Die rechte Abbildung zeigt das durch Aneinanderreihen von mehreren Miniquadraten sehr deutlich.
Nach dieser Methode ist es möglich, auch andere, größere ungerade Quadrate zu bilden.
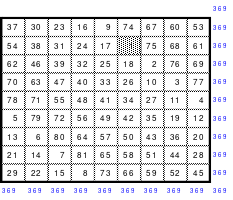
Als Beispiel das linke magisches Quadrat mit 5 x 5 = 25 Zellen und einer magischen Summe von 65. Das Quadrat ist assoziativ. Weitere Eigenschaften sind nicht gegeben. Dies trifft auch auf das rechte 9er Quadrat mit einer magischen Summe von 369 zu. Die Bildung der Quadrate erfolgt sehr einfach.
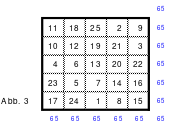
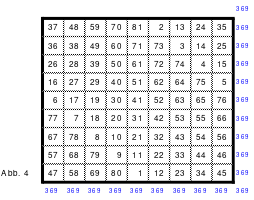
Quadrat der 5. Ordnung Quadrat der 9. Ordnung
In die Mitte der unteren Zeile wird die 1 eingesetzt. Von dort aus wird stets 1 nach rechts und 1 nach unten gegangen und die Zelle für die nächste Zahl ist gefunden. Ist diese Zelle bereits belegt, so muss 1 nach oben gegangen werden. Das bedeutet, dass jeweils ein Zahlenblock in jeweils eine geteilte Diagonale kommt, bis auf den mittleren Block, der in eine Hauptdiagonale eingeschrieben wird.
Lo Shu ein Staffelquadrat
Wieder war es das Miniquadrat das Mag zur Bildung magischer Quadrate durch die Staffelmethode führte.
Zur besseren Übersicht hat Mag das Miniquadrat um seine waagerechte Achse gedreht und erhielt so das Quadrat 1. Auffallend sind die Zahlen 4, 5 und 6. Diese sind in der aufsteigenden Diagonalen enthalten. Mag verschob die linke Spalte nach oben und die rechte nach unten mit dem Ergebnis, dass sich die 4, 5 und 6 nun in einer Zeile befinden (Abb., 2). Die aus dem Quadrat geschobenen Zahlen 8 und 2 setzte er in die frei gewordenen Zellen der gleichen Spalten ein und erhielt so das Quadrat 3. Jetzt folgte das Gleiche in horizontaler Richtung, was zum Quadrat 4 und nach der Einordnung in die leeren Zellen, zum Quadrat 5 führte. Das Endergebnis ist ein 3 x 3 großes Folgequadrat.
Mit dieser Erkenntnis müssten doch auch größere Quadrate gebildet werden können.
Der Vorgang muss nur in umgekehrter Reihenfolge durchgeführt werden. Das heißt:
Bildung eines Folgequadrates
Staffelförmige Verschiebung der Zeilen nach rechts und links, wobei die mittlere Spalte nicht verschoben werden darf
Die aus dem Quadrat geschobenen Zahlen sind in die frei gewordenen Zellen der gleichen Zeile einzusetzen.
Gleiche Behandlung der Spalten wie vor.
Von Bedeutung ist, dass das Verschieben sowohl waagerecht als auch senkrecht über die gleichen Ecken erfolgt. Im Beispiel sind es die Ecken rechts oben und links unten. Das bedeutet gleichzeitig, dass keine Zahl zweimal aus dem Quadrat verschoben werden darf.
Damit hat Mag bereits die zu beachtenden Regeln formuliert und die Bildung weiterer Quadrate kann erfolgen.
Dieses Verfahren der Quadratbildung ist die Staffelmethode.
Das Staffelquadrat der 5. Ordnung
Die Abb. 1 bis 6 zeigen die Entstehung des 5er Staffelquadrates. Weitere Erklärungen sind dazu nicht erforderlich.
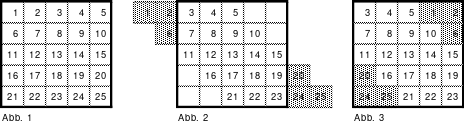
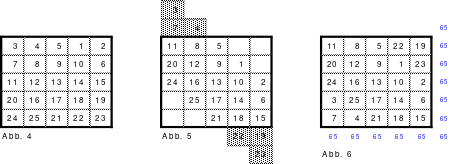
Das fertige Quadrat nach Abb. 6 ist ein assoziatives Quadrat, dessen Aufbau dem Diagonalquadrat gleicht. Als Besonderheit ist auf die Position der 1 zu verweisen, die sich im Gegensatz zu den Diagonalquadraten auf der Diagonalen befindet.
Auch die Übergänge von Block zu Block sind verändert. Diese sind 2 Zellen waagerecht und 3 Zellen senkrecht, was auf alle Staffelquadrate zutrifft.
Das 7er Staffelquadrat
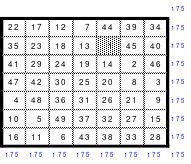
Auch das 7er Staffelquadrat ist assoziativ und gleicht dem Diagonalquadrat. Auch hier ist die Position der 1 interessant, wobei sie nicht mit der Position im 5er Quadrat identisch ist.
Das 9er Staffelquadrat
Auch bei dem 9er Staffelquadrat handelt es sich um ein Diagonalquadrat. Die 1 ist auch hier nicht auf der mittleren Spalte oder mittleren Zeile zu finden. Vergleicht man das 5er, 7er und das 9er, so ergibt sich, dass sich die 1 stets in der Zelle befindet, die sich in der 2. Reihe, rechts neben der mittleren Spalte befindet.
Eine weitere Abweichung zum Diagonalquadrat besteht darin, dass die Eintragung der Zahlen in Richtung Mitte erfolgt. Auch die Übergänge zu den nächsten Blöcken weichen von den Diagonalquadraten ab. Sie sind im 5er, 7er und 9er einheitlich 2 nach rechts, 3 nach unten.
Damit besteht die Möglichkeit die Staffelquadrate auch ohne Verschiebungen der Zellen zu bilden. Man muss nur die 1 in eine entsprechende Zelle einfügen und dann die Diagonalen ausfüllen.
Wie die Diagonalmethode ist auch die Staffelmethode nicht für die Bildung gerader Quadrate geeignet.
Wenn Mag diesen Abschnitt jetzt hier abschließt, so ist dies noch nicht der Schluss der Abhandlung der Staffelquadrate. Mag wird sich in den Abschnitten “Primquadrate” und “Triquadrate” nochmals mit der Staffelmethode befassen.
Lo Shu ein Rahmenquadrat
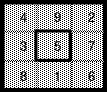
Mag hatte im Vorwort darauf hingewiesen, dass seine Ausführungen zu den magischen Quadraten unter anderem auch vom Miniquadrat abgeleitet wurden. Dies trifft auch voll und ganz auf die Rahmenmethode zu, denn das Miniquadrat ist ein Rahmenquadrat und zwar das kleinstmögliche.
Im Miniquadrat sind die Zahlen von 1 bis 9 enthalten. Die mittlere Zahl, die 5, ist als so genannter Kern in der Mitte angeordnet. Um diesen Kern sind die restlichen 8 Zahlen als Rahmen so angeordnet, dass sie sich die gegenüber liegenden Zahlen stets zu der Summe von 10 ergänzen. Diese Zahlenpaare nennt Mag Duos, weil sie sich aus jeweils 2 Zahlen zusammensetzen. Wichtig ist dabei, dass auch die diagonal zueinander liegenden Zahlen Duos sind. Im Miniquadrat sind es die Duos 4 mit 6 und 2 mit 8. Weitere Informationen erhalten Sie aus den nachstehenden Abbildungen.
Mag geht nun davon aus, dass diese Erkenntnisse auch auf andere Quadrate übertragbar sein müssen. Im Wesentlichen unterscheiden sich die Rahmenquadrate in gerade und ungerade. Es zeigt sich, dass die Bildung der geraden Rahmenquadrate wesentlich leichter ist. Auch die Gestaltungsmöglichkeiten sind umfassender. Deshalb zeigt Mag als Nächstes die Bildung eines geraden Rahmenquadraten.
Ein 6er Rahmenquadrat
Mag beginnt mit der Bildung eines Rahmenquadrates der 6. Ordnung. Dazu muss um ein 4er Quadrat, im Beispiel das Topquadrat, ein 6er Rahmen gelegt werden. Wie beim Miniquadrat werden die mittleren Zahlen dem 4er Kernquadrat zugeordnet und dem Rahmen die restlichen Zahlen.
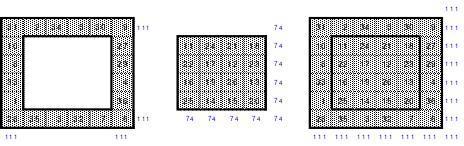
Insgesamt kommen 6 x 6 = 36 Zahlen zur Anwendung, die unten als Duos dargestellt sind. Gleichzeitig wurden die Duos für den Rahmen grün und die für das Kernquadrat blau hinterlegt. Duos sind Zahlenpaare, deren Summen einheitlich groß sind, im Beispiel 37.
Aus den Duos für den Rahmen ist dieser zu bilden, wobei je 1 Duo in die gleiche Zeile, Spalte oder Diagonale einzusetzen ist.
Die erforderliche magische Summe von 111 ((6*6+1) /2*6=111) ist durch Seitenwechsel oder Austausch vorzunehmen. Der fertige Rahmen ist links abgebildet.
In das Topquadrat werden die für dieses vorgemerkten Zahlen von 11 bis 26 anstelle der Zahlen von 1 bis 16 eingesetzt. Zum Schluss werden Topquadrat und in Rahmen zum 6er Rahmenquadrat zusammengesetzt.
Damit ist das Rahmenquadrat, auch Schachtelquadrat genannt, fertig. Es besteht aus einem Kernquadrat, ein Quadrat der 4. Ordnung. Dieses Quadrat ist magisch mit der magischen Summe von 74. Das so entstandene 6er Quadrat ist ebenfalls magisch mit der magischen Summe von 111.
Natürlich sind noch andere Lösungen möglich. Nachfolgend sind 2 weitere Rahmen zu sehen.
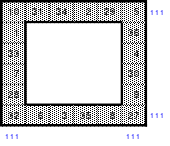
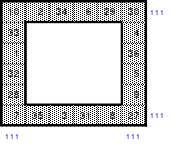
Der linke Rahmen ist ebenfalls pendelbar und distributiv. Der rechte jedoch nur distributiv, denn in den Zeilen sind 5 gerade und nur 1 ungerade Zahl, bzw. umgekehrt 5 ungerade und 1 gerade Zahl enthalten. Beide Rahmen haben die richtige magische Summe von 111.
Für eine unterschiedliche Gestaltung von geraden Rahmenquadraten hat Mag weitere Optionen herausgearbeitet. Diese unterscheiden sich in einer unterschiedlichen Zuordnung der Duos für den Rahmen und das Kernquadrat.
Als Kernquadrat kann praktisch auch ein Quadrat anderer Größe eingesetzt werden.
Es können auch Schachtelquadrate mit mehreren Rahmen gebildet werden.
Ein Beispiel ist ein Schachtelquadrat der 9. Ordnung, bei dem ein Miniquadrat in 3 Rahmen eingeordnet ist.
Nachstehend ist die dazu erforderliche Duokette zu sehen.
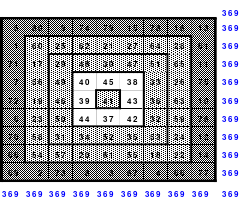
Das abgebildete Schachtelquadrat enthält 4 magische Quadrate der 3.; 5.; 7. und 9. Ordnung, deren magische Summen 123, 205, 287 und 399 sind. Alle Zahlen von 1 bis 81 sind lückenlos und nur einmal vorhanden.
Mag hat eine konstruktiv-mathematische Methode zur Bildung der Rahmen entwickelt. Dieses Verfahren kann grundsätzlich für alle Rahmen angewendet werden. Dabei zeigt sich, dass die Bildung mit zunehmender Größe immer leichter wird.
Von weiteren Erläuterungen zu den Rahmenquadraten nimmt Mag Abstand, da diese keinen Eingang in das Hexen 1x1 finden.
Lo Shu ein Springerquadrat
Anfangs war Mag stolz auf seine Entdeckung der Springermethode, die er durch den Tausch von Spalten in einem 5er Diagonalquadrat gefunden hatte. Dieser Stolz ist nun verflogen. Erst nach den beschriebenen Varianten der Springermethode hat Mag das Miniquadrat analysiert und feststellen müssen, dass dieses ein Springerquadrat ist.
Dabei hat Mag 2 Varianten gefunden. Bei der 1. Variante sind die Bewegungen innerhalb der Blöcke 2 nach oben und 1 nach rechts und von Block zu Block 1 nach oben. Abb. 1 zeigt das sehr deutlich durch die angefügten Hilfsquadrate, die die Positionen der Zahlen im Miniquadrat besser verdeutlichen.
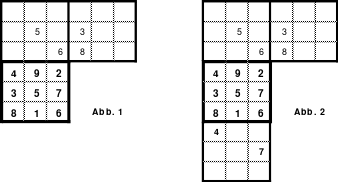
Die in Abb. 2 gezeigte 2. Variante beinhaltet als Bewegungen innerhalb der Blöcke 2 nach oben und 1 nach rechts, so wie bei Variante 1. Jedoch ist der Übergang von Block zu Block hier nicht 1 nach oben, sondern 2 nach unten. (Was letztlich dasselbe ist, aber nur für das Lo-Shu-Quadrat!)
Wie diese Erkenntnisse praktisch angewendet werden, wird in den Abschnitten “Primquadrate” und “Triquadrate” gezeigt.
3.1.2. Primquadrate
Die Springermethode ermöglicht die Bildung von ungeraden Quadraten mit unterschiedlicher Qualität. Mag unterscheidet im Wesentlichen 2 Gruppen:
Die Primquadrate
Die Primquadrate sind pandiagonale, ungerade, homogene und magische Quadrate. Sie sind die perfekten Quadrate, weil sie die wichtigsten Bedingungen für die Arbeit im Hexeneinmaleins erfüllen. Diese sind neben der Pandiagonalität die Homogenität. Des Weiteren kann die Form des Springens nahezu frei gewählt werden. Sie entstehen bei Quadraten, deren Ordnungszahl eine Primzahl ist. Mag nennt diese deshalb auch “Primquadrate”.
Die Triquadrate
Triquadrate sind ungerade Quadrate, deren Ordnungszahlen keine Primzahlen sind. Dabei handelt es sich meist um Quadrate, deren Ordnungszahl durch 3 teilbar ist. Mag nennt sie deshalb “Triquadrate”. Die Triquadrate haben nicht die Qualität der Primquadrate.
(Siehe dazu unter “Triquadrate”)
Die Springerquadrate stellen neben den Diagonalquadraten die größte Gruppe der ungeraden magischer Soloquadrate dar.
Dabei sind die Springerquadrate gegenüber den Diagonalquadraten die qualitativ besseren. Mit der Springermethode können praktisch alle ungeraden Quadrate gebildet werden und damit 50 % aller Quadrate, was bei den anderen Methoden nicht möglich ist.
Das Pentaquadrat
Als sich Mag intensiv mit dem Hexeneinmaleins beschäftigte, suchte er nach einem 5 x 5 Zellen großes Quadrat, das für die Experimente des Hexeneinmaleins wie das Topquadrat angewendet werden kann.
Das geschah, bevor Mag das Lo-Shu-Quadrat einer Analyse unterzog.
Mag wollte schon die Suche nach einer Lösung aufgeben, als er doch noch überraschend zu einem Ergebnis kam. Grundlage seiner Untersuchungen war das 5er Diaganolquadrat, wie es unter “Diagonalquadrate” beschrieben wurde und als linkes abgebildet ist.
Er hatte die 3. senkrechte Reihe als 1. senkrechte Reihe,
" 1. “ “ “ 2. " " ,
" 4. " “ “ 3. " " ,
" 2. " " “ 4. " " gesetzt und
" 5. " “ “ 5. “ " belassen.
So entstand das mittlere Quadrat, das die wichtigsten Bedingungen für die Arbeit im Hexeneinmaleins erfüllt. In jeder Reihe befindet sich jeweils eine Zahl aus jedem Block, so auch die grün markierten großen Zahlen 21 bis 25. Die Zahlen der 5 Blöcke sind: 1 bis 5. 6 bis 10, 11 bis 15, 16 bis 20 und 21 bis 25. Damit ist dieses Quadrat ein homogenes. Es ist auch ein pandiagonales, weshalb die Zeilen d und e auch nach oben versetzt werden konnten. Das so entstandene magische Quadrat mit der magischen Summe von 65 hat Mag den Namen “Pentaquadrat” gegeben.
Als Mag dieses magische Quadrat einer umfassenden Analyse unterzog, erkannte er einige interessante Gesetzmäßigkeiten.
Die Zahlen jedes Blockes sind nach einem einheitlichen Schema geordnet. Beginnend mit der 1. Zahl sind die folgenden jeweils 1 Feld tiefer und 2 Felder nach rechts eingeordnet. Dabei gilt auch hier, kommt man zu einer Begrenzungslinie, so ist von der gegenüber liegender Begrenzungslinie weiter zu zählen. Ist der Block fertig eingetragen und geht man in gleicher Weise weiter, so kommt man auf die 1. Zahl dieses Blockes. Es ist folglich ein in sich geschlossener Ring. Geht man z. B. von der Zahl 5 eine Zelle nach unten und 2 Zellen nach rechts, so kommt man auf die Zelle mit der Zahl 1.
Die 1. Zahl des folgenden Blockes steht immer 2 Felder unter der letzten des vorangegangenen Blockes. So z. B. die 6 zwei Zellen unter der 5.
Danach erfolgt die Eintragung der übrigen Zahlen des Blockes wie gehabt, 1 Zelle nach unten und 2 Zellen nach rechts. Geht man nach Eintragung der letzten Zahl, der 25, 2 Zellen nach unten, so kommt man auf Zelle mit der Zahl 1. Damit steht fest, das gesamte System ist ein geschlossener Ring. Es können auch beliebig viele Zeilen von oben nach unten, oder Spalten von links nach rechts und umgekehrt verschoben werden, es bleibt stets ein magisches Quadrat. Damit ist das Pentaquadrat ein pandiagonales. Zum Beweis der gefundenen Gesetzmäßigkeiten, besonders der letzten, hat Mag 2 mal 2 Pentaquadrate zum untenstehenden 10 mal 10 großen Quadrat zusammengefügt.
Es ist gleich, welches 5 mal 5 große Quadrat ausgewählt wird, es ist immer ein pandiagonales magisches Quadrat mit der magischen Summe 65. In jedem Quadrat, ob blau, rot oder grün eingefassten Quadrat findet man in jeder Reihe, auch in den Diagonalen, je eine Zahl aus jeden Zahlenblock, so auch die großen Zahlen 21 bis 25.
Damit ist das Pentaquadrat teilweise sogar dem vollkommenen magischen Quadrat, dem Topquadrat, überlegen. Denn beim Topquadrat ist es nicht möglich, einzelne Reihen zu verschieben. Stets müssen 2 Reihen verschoben werden, damit auch in jeder Diagonalen eine der großen Zahlen enthalten ist, eine Bedingung, die für mehrere Darbietungen im Hexeneinmaleins unverzichtbar ist.
(Das Topquadrat wird im Abschnitt gerade Quadrate beschrieben.)
Auch der Aufbau des Pentaquadrates ist im Vergleich zum Topquadrat viel einfacher. Man muss sich nur merken, 1 nach unten 2 nach rechts, das ist auch 2 waagerecht und 1 nach unten, ein Rösselsprung. Ist ein Block eingetragen, so geht es einfach 2 Felder nach unten und die Zahlen des nächsten Blockes werden wie gehabt eingesetzt. Das ist 2 Zellen nach rechts und 1 Zelle nach unten.
Das Pentaquadrat hat allerdings gegenüber dem Topquadrat auch Nachteile. So kann das Pentaquadrat wegen seiner ungeraden Zellenzahl nur bedingt für Pendelquadrate eingesetzt werden. Auch die Untergliederung in Teilquadrate ist nicht möglich.
Da die 5 Zeilen, wie auch die 5 Spalten senkrecht bzw. waagerecht verschoben werden können, sind 5 x 5 = 25 verschiedene magische Quadrate möglich.
Mag hatte eingangs die Aussage getroffen, dass das Springen selbst bei den Primquadraten nahezu frei gewählt werden kann. Das heißt, nicht alle Kombinationen führen zum Erfolg, höchstens zu einem Teilerfolg.
So scheiterte u. a. der Versuch ein 5-er Quadrat mit den Werten 1 nach unten und 2 nach links innerhalb der Blöcke und 1 nach oben von Block zu Block. Das Quadrat konnte reibungslos konstruiert werden, aber es war kein magisches. Alle waagerechten und senkrechten Reihen wiesen die richtige magische Summe von 65 aus, bei den Diagonalen jedoch nur die fallende. Die steigende Diagonale hatte als Summe nur 60. Als Mag für alle geteilten Diagonalen die Summen ermittelte, stellte er fest, dass alle fallenden geteilten Diagonalen die richtige magische Summe von 65 haben, bei den steigenden jedoch nur eine. Nach der Verschiebung der untersten Zeile nach oben kam die geteilte steigende Diagonale mit der magischen Summe von 65 an die Stelle der steigenden Hauptdiagonale. Damit war das Quadrat magisch und auch homogen, aber nicht mehr pandiagonal und damit nicht perfekt.
Nachstehend wird das Gesagte dargestellt.
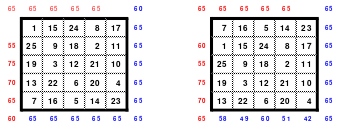
Auch der Versuch mit 1 senkrecht nach unten und 3 nach rechts im Block und 3 nach links von Block zu Block brachte kein magisches Quadrat hervor.
Andere Kombinationen dagegen führten zu einem guten Ergebnis. Es gilt deshalb stets zu prüfen, ob die gewählte Variante auch zum Erfolg führt. Dabei gilt, was bei einem kleinen Primquadrat zu einer Lösung führt, kann auch für größere Primquadrate eingesetzt werden.
Das Heptaquadrat
Ausgehend von der Struktur des Pentaquadrates bildete Mag ein Springerquadrat der 7. Ordnung. Dabei wurde ebenfalls innerhalb der Blöcke jeweils 2 nach rechts und 1 nach unten und von Block zu Block 2 nach unten gegangen. Das Ergebnis ist ein perfektes Quadrat der 7. Ordnung. Es ist pandiagonal und homogen. Damit ist dieses Quadrat ebenfalls gut im Hexeneinmaleins einsetzbar.
Mag kommt nochmals auf seine Aussage der nahezu freien Wahl des Springens zurück. Er bildete ein ebenfalls 7er Quadrat, indem er die einzelnen Schritte verdoppelte. Also 4 nach rechts und 2 nach unten innerhalb der Blöcke und 4 nach unten von Block zu Block. Mag bezeichnet diese Art des Springens als Doppelsprung. Das Ergebnis ist auch ein magisches, pandiagonales und homogenes, also perfektes Quadrat.
Die beiden Quadrate sind nachfolgend dargestellt.
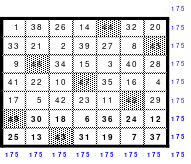
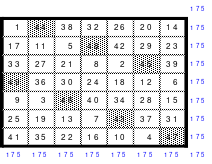
Einfacher Sprung Doppelsprung
Keine perfekten Quadrate
Von den Ergebnissen beflügelt machte sich Mag sofort daran ein 9er Quadrat zu bilden und scheiterte. Egal welche Variante er wählte, ein magisches Quadrat kam nicht zustande. In einigen Fällen konnte selbst das Quadrat nicht konstruiert werden. Es kam zu Deckungen der Zellen, das heißt, dass die folgende Zelle die nächste Zahl nicht aufnehmen konnte, weil diese schon belegt war. Mag war ziemlich ratlos. Wieso gab es keine Lösung? Das 9er Quadrat ist doch genauso ein ungerades wie das 5er Pentaquadrat oder das 7er Heptaquadrat. Mag suchte nach einer Begründung. Erst als er den scheinbar unbedeutenden Unterschied zwischen den Zahlen nachging, fand er des Rätsels Lösung. Dieser Unterschied, den Mag nicht für ausschlaggebend gehalten hatte war der, dass die 5 und 7 Primzahlen sind, die 9 aber nicht. Dass diese Erkenntnis richtig, oder fast richtig ist, zeigte sich sehr schnell. Denn Mag konnte ohne Schwierigkeiten das 11er und 13er Quadrat als perfekte magische Quadrate bilden, denn diese waren die nächsten Primzahlen. Bei der Bildung eines perfekten 15er Quadrat scheiterte Mag wieder, denn die 15 ist auch keine Primzahl.
(Die erwähnten Quadrate der 11. und 13. Ordnung finden Sie im Anhang in der Datei “Quadrateparade”.)
Wenn Mag sagt, dass diese Erkenntnis “fast richtig” ist, dann aus gutem Grund, denn die Bildung von Springerquadraten mit einer Ordnungszahl, die keine Primzahl ist, ist möglich. Nur die Bildung solcher Quadrate als perfekte, pandiagonale Quadrate ist nicht erreichbar. Mag wird dazu noch nähere Ausführungen im Abschnitt “Triquadrate” machen.
Vom Staffelquadrat zum Springerquadrat
Mag hatte bei der Behandlung der Staffelquadrate bereits angekündigt, dass die Staffelquadrate nochmals eine Rolle bei den Springerquadraten spielen werden. Das soll nun erfolgen.
Das Quadrat 1 ist das 5er Staffelquadrat. Werden wie bei der Staffelmethode nochmals die Zellen gestaffelt, und anschließend eingeordnet, so wie es die Abb. 2 und 3 zeigen, entsteht ein Springerquadrat. Die Bewegungen innerhalb der Blöcke sind 1 nach rechts und 2 nach unten und von Block zu Block 2 nach rechts.
Die Staffelung erfolgte hierbei vertikal.
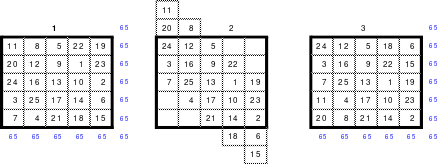
Natürlich kann die Staffelung auch horizontal erfolgen. Auch hier entsteht ein Springerquadrat wie es die Abb. 4 und 5 zeigen.
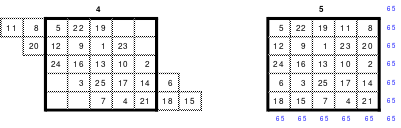Verbotene
Schritte
Mag hatte mehrmals darauf hingewiesen, dass die Wahl der Schritte bei der Bildung von Primquadraten nahezu beliebig ist. Mit ´nahezu´ hat Mag angedeutet, dass nicht jede Schrittwahl zum Ergebnis führt.
Das trifft insbesondere auf die Übergänge von Block zu Block zu. Würde hier die Schrittwahl einer der Bewegungen innerhalb des Blockes entsprechen, so würde die erste Zahl des folgenden Blockes in die Spalte bzw. Zeile der ersten Zahl des vorangegangenen Blockes kommen. Die Summe aller ersten Zahlen in der Spalte bzw. Zeile ergeben nicht die magische Summe. So sind z. B. die ersten Zahlen der Blöcke in einem Quadrat der 5. Ordnung 1 + 6 + 11 + 16 + 21 = 55 und nicht 65. Gleiches trifft zu 50% bei einer Schrittgröße von Block zu Block zu, die der Differenz oder der Summe der beiden Schrittgrößen innerhalb der Blöcke entsprechen, wobei die Richtung von Bedeutung ist. Bei diesen Fällen würden die ersten Zahlen der Blöcke in die Diagonalen kommen, wodurch das Quadrat kein pandiagonales magisches Quadrat wird.
Mag möchte nun das Gesagte am Beispiel eines Quadrates der 13. Ordnung demonstrieren. Als Schritte innerhalb der Blöcke hat Mag 5 nach rechts und 3 nach unten gewählt. Da die Zahlenketten im Quadrat geschlossene Ringe bilden, würde man von der letzten Zahl des ersten Blockes, der 13, bei der Bewegung 5 nach rechts und 3 nach unten auf die Zelle stoßen, in der bereits die 1 enthalten ist. Entsprechend dieser Kenntnis findet man von der 1 ausgehend die Zelle 13. Man muss nur 3 nach oben und 5 nach links gehen. Alle Reihen, die die Zelle 1 kreuzen sind rot gekennzeichnet. In keine dieser gekennzeichneten Zellen darf nun die erste Zahl des folgenden Blockes, hier die 14, eingesetzt werden. Bei einem Übergang 5 nach rechts käme die 14 in die mit a gekennzeichnete Zelle, was nicht sein darf. Bei 3 nach unten würde die Zelle b erreicht. Bei einer Bewegung entsprechend der Differenz 5 - 3 = 2, trifft man auf die Zellen c und d. Zu den Zellen e und f gelangt man bei einer Bewegung nach rechts oder nach unten, wenn die Schrittgröße der Summe 5 + 3 = 8 entspricht.
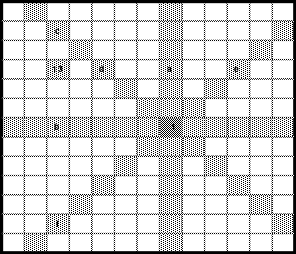
Wählt man die Bewegung so, dass eine nicht rot markierte Zelle erreicht wird, so besteht eine gute Voraussetzung zum Gelingen des pandiagonalen magischen Quadrates.
3.1.3. Triquadrate
Wie schon gesagt, der Versuch durch einfaches Springen ein magisches 9er Quadrat zu erstellen scheiterte. Das linke Quadrat zeigt das Ergebnis. Die steigende Diagonale hatte zwar die richtige magische Summe von 369, die fallende mit einer Summe von 360 jedoch nicht. Als Mag die geteilten Diagonalen berechnete, fand er, dass sowohl jede 3. fallende als auch jede 3. steigende Diagonale den richtigen Wert von 369 ergab.
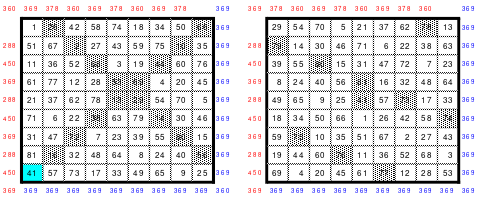
Für das Hexen 1x1 geeignet
Weiter fand er, dass die mittlere Zahl 41 in einer fallenden und steigenden Diagonalen mit der magischen Summe von 369 zu finden war. Er verschob die Zeilen und Spalten so, dass die 41 in die Mitte des Quadrates positioniert war. Das Ergebnis ist das rechte magische, assoziative Quadrat. Es ist allerdings nicht pandiagonal und damit auch nicht perfekt. Es ist auch nicht homogen. Unter Beachtung bestimmter Bedingungen kann es im Hexen 1x1 eingesetzt werden.
Durch den direkten Tausch der Spalten 1 und 9, sowie den indirekten Tausch der Spalten 2 mit 3 und 7 mit 8 kann zumindest ein teilhomogenes magisches Quadrat erreicht werden. Dieser Tausch ist möglich, da es sich um ein assoziatives Quadrat handelt.
Die nächste Überraschung erlebte Mag als er ein 9er Quadrat im Doppelsprung bilden wollte. Er setzte die 1 unter die mittlere Zelle des Quadrates und füllte dann im Doppelsprung alle anderen Zellen aus.
Nachdem das Quadrat fertig war, befand sich nicht die 41 in der Mitte des Quadrates, sondern die 21. Auch das Quadrat war nicht magisch, denn nicht beide Diagonalen hatten die magische Summe. Erst als Mag die unterste Zeile nach oben versetzte, war ein magisches Quadrat entstanden. Es ist das linke, ein assoziatives, aber nicht homogenes magisches Quadrat. Aber auch hier konnte durch den Tausch der 2. mit der 7. und der 3. mit der 8. Spalte ein teilhomogenes, assoziatives magisches Quadrat erreicht werden. Es ist das rechte Quadrat.
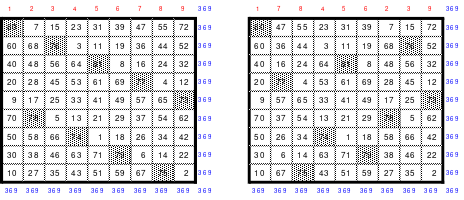
Die mit der Springermethode erstellten Quadrate der 9. Ordnung sind nicht so unflexibel wie es scheint. Da jede dritte fallende und steigende Diagonale, auch die geteilten, die richtige magische Summe hat, können jeweils 3 Spalten und/oder 3 Zeilen versetzt werden. Das ist jedoch nicht mehr möglich, wenn durch Tausch von Zeilen bzw. Spalten eine Teilhomogenität hergestellt wurde. Das folgende Quadrat entstand aus dem oberen linken Quadrat durch Versetzen der ersten 3 Zeilen nach unten und der ersten 3 Spalten nach hinten. Das so entstandene Quadrat ist ein magisches, jedoch nicht mehr assoziativ.
Auf einen Schönheitsfehler muss hingewiesen werden. Die letzten Ziffern der Zahlen einer Spalte sind bis auf wenige Ausnahmen gleich. So ist z. B. die letzte Ziffer der Zahlen in der 2. Spalte nur 1. In der 1. Spalte ist es die 3, wobei lediglich 2-mal die 4 zu finden ist.
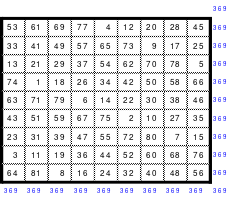
Ausgehend von den Erkenntnissen kann nun ein magisches Quadrat der 15. Ordnung gebildet werden. In die Mitte des 15 x 15 großen Quadrates wird die mittlere Zahl, die 113, eingesetzt. Da die Variante des Doppelsprunges angewendet wird, ist die 1 im Abstand von 2 Zellen unterhalb der 113 einzusetzen. Dann folgt die Eintragung aller weiteren Zahlen im Doppelsprung.
Das fertige Quadrat ist ein magisches mit der magischen Summe von 1695. Es ist auch assoziativ, jedoch nicht homogen. Aber durch den Tausch der 1. mit der 2. und der 14. mit der 15. Spalte wird ein teilhomogenes Quadrat erreicht.
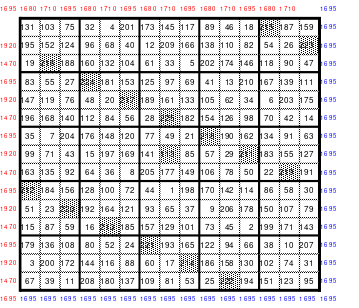
Dieses Quadrat der 15. Ordnung hält eine besondere Überraschung bereit. Mag teilte das Quadrat in 3 x 3 große Teilquadrate und übernahm alle mittleren Zahlen unter Beibehaltung der Ordnung in ein 5er Quadrat. Das linke Quadrat zeigt dies. Als Mag diese Zahlen nach ihrer Größe ordnete und entsprechend der Reihenfolge die Zahlen mit den Zahlen von 1 bis 25 ersetzte erhielt er als Ergebnis das rechte Quadrat der 5. Ordnung. Es ist ein pandiagonales, homogenes, magisches Quadrat. Es ist ein Springerquadrat. Die Zahlen innerhalb der Blöcke sind 2 nach unten und 1 nach links eingeordnet. Die Bewegung von Block zu Block ist 1 nach oben. Dies ist im rechten Quadrat zu erkennen. Hier sind die Zahlen von 1 bis 25 entsprechend der Größenordnung des linken Quadrates eingesetzt worden.
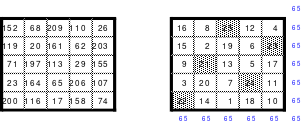
Nach dieser Überraschung bildete Mag ein 15er Quadrat durch einfaches Springen. Als er hier ebenfalls die mittleren Zahlen nach dem gleichen Prinzip ordnete und durch die Zahlen 1 bis 25 ersetzte, fand er ein weiteres magisches Quadrat der 5. Ordnung. Die Zahlen sind nicht wie oben rechts geordnet, sondern völlig anders, wobei die vorhandene Regelmäßigkeit nur schwer erkennbar ist. Das so gefundene neue Quadrat ist links abgebildet.
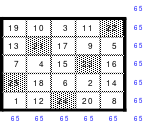
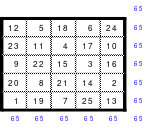
Vom Ergebnis beflügelt untersuchte Mag nun ein magisches Quadrat der 25. Ordnung, dass wegen der Größe hier nicht abgebildet werden kann. Er wählte ein freies Springen, wobei die Bewegungsgrößen innerhalb der Blöcke 9 waagerecht nach rechts und 4 senkrecht nach unten und von Block zu Block 7 waagerecht nach rechts betrugen. Auch hier betrugen die Summen der Diagonalen nicht immer der richtigen magischen Summe, sondern nur jede fünfte. Nach Versetzen der entsprechenden Reihen und Spalten war ein magisches Quadrat mit der magischen Summe von 7825 entstanden. Auch dieses Quadrat war kein homogenes.
Wie bei den 15er Quadraten unterteilte Mag das Quadrat in 25 Teilquadrate mit der Größe von 5 x 5 Zellen. Wieder wurden die mittleren Zahlen in ein 5er Quadrat eingeordnet und entsprechend ihrer Größe durch die Zahlen von 1 bis 25 ersetzt. Auch dieses Ergebnis war eine Überraschung. Es ist das rechts abgebildete Quadrat. Es ist ein Diagonalquadrat, wobei die 1 unten links in der Ecke zu finden ist. In der Mitte ist nicht wie üblich die mittlere Zahl, die 13, sondern die 15 positioniert. Weitere interessante Details sind der Abbildung zu entnehmen.
Weitere Untersuchungen hat Mag nicht vorgenommen. Er ist sich aber sicher, dass z. B. ein 21er Springerquadrat nach einer Unterteilung in 3 x 3 große Teilquadrate und entsprechende Einordnung in ein 7er Quadrat, ein völlig neues magisches Quadrat der 7. Ordnung ergibt.
Vom Staffelquadrat zum Springerquadrat
Mag hatte bei der Behandlung der Staffelquadrate im Abschnitt “Lehrmeister Lo-Shu” bereits angekündigt, dass die Staffelquadrate nochmals eine Rolle bei den Springerquadraten spielen werden. Das trifft, wie nachfolgend gezeigt, auch auf die Triquadrate zu.
Als Mag das 9er Staffelquadrat wie das 5er staffelte, entstand kein magisches Quadrat. Erst als er das links abgebildete 9er Staffelquadrat 2-mal, jeweils 1-mal waagerecht und 1-mal senkrecht staffelte, entstand das rechte magische Springerquadrat. (Nächste Seite)
Die Schritte sind dabei im Block 5 nach rechts und 1 nach oben und von Block zu Block 3 nach unten und 4 nach rechts. Es ist leider auch kein pandiagonales Quadrat, sondern lediglich ein assoziatives. Es ist auch nicht homogen oder wenigstens teilhomogen, denn in der fallenden Diagonalen ist keine der großen Zahlen von 73 bis 81 enthalten.
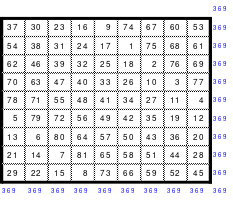
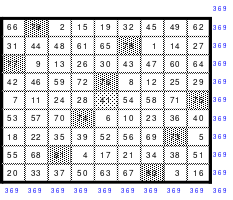
Ein Tausch nach dem Reihen- oder Rautenprinzip brachte kein Ergebnis. Stets waren mehr als eine der großen Zahlen in der fallenden Diagonale zu finden. Eine Lösung durch Zahlentausch, Mag nennt dies die Puzzlemethode, lehnt Mag im Allgemeinen ab. Trotzdem versuchte er sein Glück, allerdings ergebnislos. Doch dann machte er eine Entdeckung. Die beiden Quatros in den oberen Ecken hatten gleiche Summen der Diagonalen. Im linken Quattro 110 und im rechten 76. Dadurch konnten die beiden oberen Zeilen getauscht werden, ohne dabei die Diagonalen des Gesamtquadrates zu verändern. Durch den Tausch der 1. mit der 2. Zeile war das folgende zumindest teilhomogene magische Quadrat der 9. Ordnung erstellt.
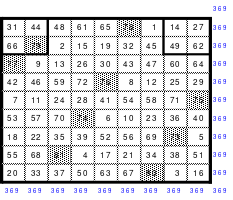
Die in Abb. 2 gezeigte 2. Variante beinhaltet als Bewegungen innerhalb der Blöcke 2 nach oben und 1 nach rechts, so wie bei Variante 1. Jedoch ist der Übergang von Block zu Block hier nicht 1 nach oben, sondern 2 nach unten.
Mag bildete nach Variante 2 ein 9er Quadrat erfolgreich. Es ist ein assoziatives magisches Quadrat. Die Berechnung der fallenden und steigenden geteilten Diagonalen ergab, dass jede 3. die richtige magische Summe von 369 hat. Nachteilig ist auch hier, dass die letzten Ziffern der Zahlen einer Spalte bis auf wenige Ausnahmen stets gleich sind, so wie in vorangegangenen Beispielen.
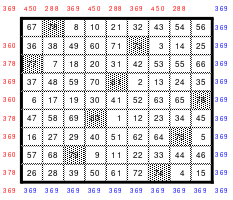
Interessante Details ergaben sich, als Mag das Quadrat in 3 x 3 große Teilquadrate teilte und diese analysierte. Alle Hauptdiagonalen der Teilquadrate hatten als magische Summe 123. Weiter zeigte sich, dass die 1., 2. und 3. Zeilen der untereinander befindlichen Teilquadrate ebenfalls die magische Summe von 369 ergeben. Als Beispiel die 1. Zeilen der vorderen Teilquadrate. Sie sind blau gekennzeichnet. Ebenso verhält es sich mit den Spalten. Auch hier ergeben die 1., 2. und 3. Spalte der 3 nebeneinander liegenden Teilquadrate die magische Summe von 369. Als Beispiel die gelb markierten 3. Spalten der mittleren Teilquadrate.
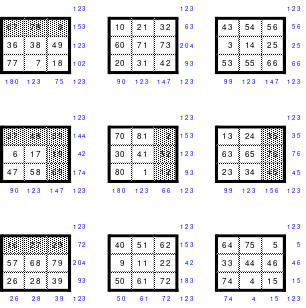
Diese Besonderheiten nutzte Mag um die vertikal angeordneten 3er Teilquadrate horizontal einzusetzen. Das Ergebnis ist das Quadrat entsprechend Abb. 2. Es ist nach wie vor ein assoziatives magisches Quadrat. Diese Umgestaltung hat den Vorteil, dass jetzt die letzten Ziffern der Zahlen sowohl in den Spalten als auch in den Zeilen nicht mehr gleich groß sind.
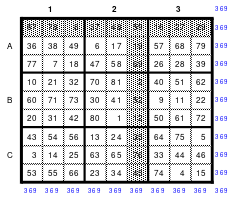
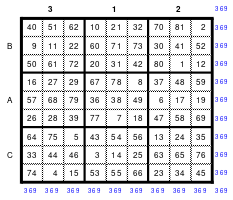
Abb. 2 Abb. 3
Da alle Diagonalen der Teilquadrate mit 123 gleich groß sind, können auch die senkrechten und waagerechten Reihen der Teilquadrate verschoben oder ausgetauscht werden. Abb. 3 zeigt das Quadrat entsprechend Abb. 2 nachdem die senkrechten Reihen der 3er Quadrate verändert wurden indem die 3. Reihe nach vorn als 1. versetzt wurde. Bei den waagerechten Reihen wurden die Reihen A und B getauscht. Dieses Quadrat ist nur noch magisch und nicht mehr assoziativ.
Die weiteren Beschreibungen basieren auf dem Quadrat nach Abb. 2. Es ist in Abb. 4 nochmals dargestellt, wobei die 9 großen Zahlen farbig hervorgehoben wurden.
In jeder Spalte und jeder Zeile befindet sich eine der großen Zahlen von 73 bis 81. Bei den Diagonalen trifft dies nur auf die steigende zu. In der fallenden Diagonale befindet sich dagegen keine dieser Zahlen. Durch den Tausch der Spalten 2 mit 3 und 7 mit 8 wurde dieser Mangel behoben. Dadurch wurde erreicht, dass das 9er Quadrat zumindest ein teilhomogenes ist und damit für die Bildung von Multiquadraten geeignet ist. Für Vorführungen ist es nicht nur wegen der Größe, sondern auch wegen der Verschiebung von Zeilen und/oder Spalten nicht einsetzbar.
Dieses Quadrat ist ein assoziatives magisches und wurde von Mag als das “Nonequadrat” benannt.
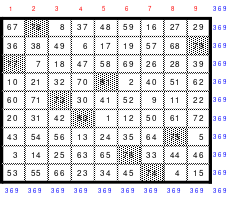
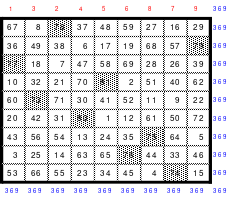
Abb. 4 Das Nonequadrat
Mit dem Nonequadrat und einer folgenden allgemein anwendbaren Regel schließt Mag diesen Abschnitt der Triquadrate als Springerquadrate ab.
In Auswertung aller bei der Bildung eines Triquadrates mittels der Springermethode gemachten Erkenntnisse kann die folgend beschriebene Regel abgeleitet werden:
Zur Erinnerung
Lo Shu ein Springerquadrat
Mag hat 2 Varianten gefunden. Bei der 1. Variante sind die Bewegungen innerhalb der Blöcke 2 nach oben und 1 nach rechts und von Block zu Block 1 nach oben. Abb. 1 zeigt, dass sehr deutlich durch die angefügten Hilfsquadrate, die die Positionen der Zahlen im Miniquadrat besser verdeutlichen. Die in Abb. 2 gezeigte 2. Variante beinhaltet als Bewegungen innerhalb der Blöcke 2 nach oben und 1 nach rechts, so wie bei Variante 1. Jedoch ist der Übergang von Block zu Block hier nicht 1 nach oben, sondern 2 nach unten. (Was letztlich dasselbe ist, aber nur für das Lo-Shu-Quadrat!)
Die Regel:
Links ist das Miniquadrat um 90o gedreht dargestellt. Darunter die daraus abgeleiteten Sprünge. Rechts ein Quadrat der 9. Ordnung untergliedert in 3 mal 3 Miniquadrate und Darstellung der Position der 1.
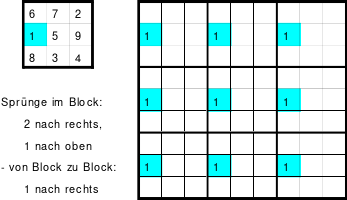
Es ist egal von welcher der 9 Zellen mit der 1 gestartet wird, wenn die folgenden Zahlen entsprechend der genannte Sprünge und Übergänge eingesetzt werden, so entsteht ein magisches Quadrat.
Das nachfolgende linke assoziative magische Quadrat der 9. Ordnung bestätigt die Richtigkeit, auch wenn es nicht gerade als ein attraktives Quadrat bezeichnet werden kann. Es ist nicht pandiagonal und weder homogen noch teilhomogen.
Durch den Tausch der letzten beiden Spalten oder auch Zeilen kann aber eine Teilhomogenität erreicht werden. Das rechte Quadrat zeigt den Tausch der beiden letzten Spalten.
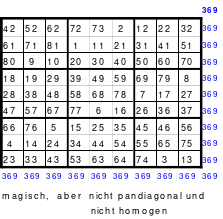
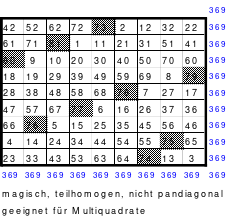
Natürlich lassen sich nach den aus dem Miniquadrat abgeleiteten Varianten auch weitere ungerade Quadrate bilden. Dabei ist es egal, ob es sich um ein Primquadrat oder ein ungerades Quadrat aus einer teilbaren Ordnungszahl handelt. Mag hat die nachfolgenden Quadrate der 15. Ordnung und der 7. Ordnung nach der Variante 2 gebildet. Dabei zeigt sich, dass das 7er Quadrat als Primquadrat ein pandiagonales perfektes Quadrat ist.
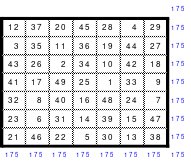
Ein Quadrat der 7. Ordnung
Bei Anwendung der 1. Variante bei einem 7er Quadrat entsteht dagegen kein pandiagonales perfektes Quadrat. Der 2. Variante ist deshalb der Vorzug zu geben, zumal hier auch die Zahlenverteilung eine günstigere ist.
Ein Quadrat der 15. Ordnung
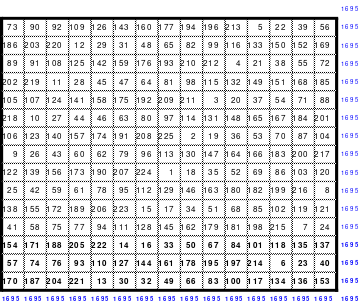
Eine Nachbetrachtung
Die im Teil “Primquadrate gegebenen Hinweise zu den verbotenen Schritten haben auch bei den Triquadraten Geltung.
Die Abhandlungen zu den Triquadraten sind sehr umfangreich. Sie wurden von Mag mehrere Jahre vor der Erstellung des Hexen 1x1 erarbeitet und waren ursprünglich für ein Buch gedacht. Von einer Kürzung hat Mag Abstand genommen, wird doch hier aufgezeigt, dass viele Wege zu den Springerquadraten führen. Dabei ist herausgearbeitet, dass nicht jede Springervariante für alle Quadrate das gewünschte Ergebnis bringt und zwischen den Primquadraten und den Triquadraten beträchtliche Qualitätsunterschiede bestehen.
Für die Erstellung von Triquadraten verweist Mag auf seine Ausführung im Abschnitt “Mosaikquadrate” Im Teil “Kombiquadrate”. Dort wird gezeigt, wie durch das Zusammenfügen von kleineren Quadraten, größeren Quadraten gebildet werden können. Dabei ist die Excel-Anwendung “Korrekturquadrate” nützlich um die erforderlichen kleineren Teilquadrate rationell zu bilden.
3.2. Gerade Quadrate
3.2.1. Das Topquadrat
Die Versuche, ein magisches Quadrat der 4. Ordnung mittels verschiedener Methoden, wie Wende- oder Fusionsmethode zu bilden, brachten keine befriedigenden Ergebnisse. Auch im Internet konnte kein 4er Quadrat gefunden werden, dass die gestellten Bedingungen erfüllten.
Diese Bedingungen sind:
Das Quadrat soll ein homogenes sein, d. h., in jeder Reihe muss eine Zahl aus jedem Block enthalten sein, wobei je eine die 1., 2., 3. und 4. Zahl eines Blockes sein muss. Diese Bedingung soll auch die gebrochenen Diagonalen erfüllen.
Das Quadrat soll pandiagonal sein, d. h., auch die gebrochenen Diagonalen müssen die magische Summe 34 ergeben.
Es muss pendelbar sein, d. h. in jeder Reihe müssen 2 gerade und 2 ungerade Zahlen eingeordnet sein,
Es kann angenommen werden, dass ein solches Quadrat der 4. Ordnung nicht möglich ist, denn alles Suchen danach war ergebnislos.
Mag versuchte deshalb, aufbauend auf die Erkenntnisse aus den Quadraten der Springermethode und dem Dürerquadrat, ein pandiagonales Quadrat der 4. Ordnung zu erstellen. Dabei ging er unter Beachtung der gestellten Bedingungen Schritt für Schritt an die Einordnung der Zahlen von 1 bis 16.
Mag ging davon aus, dass die Zuordnung der Zahlen in das Quadrat am besten durch Einordnung der einzelnen Blöcke in Duos zu erreichen ist. Er fasste den 1. und 2. Block in Duos zusammen, Die Duosumme beträgt 9. (Abb. 1 A) Die Zahlen der Blöcke 3 und 4 ergaben die Duoreihe nach Abb. 1 B. Die Duosumme ist 25 und ergibt mit der Duosumme von A die magische Summe von 34. Die Duos aus A und B mussten so zugeordnet werden, dass eine Homogenität erreicht wird. Das wurde erreicht durch eine veränderte Zuordnung der Duos, wie es Abb. 1 C zeigt. Damit waren die Zahlen in den Zeilen so angeordnet, dass die Summen einheitlich 34 sind und in jeder Zeile sich eine 1., 2., 3. und 4 Zahl eines Blockes zu finden ist, eine Bedingung für pandiagonale Quadrate.
Andere Duo-Zusammenstellungen, wie z. B. der 1. Block mit dem 4. Block, ergaben zwar magische Quadrate, sie waren aber nicht pandiagonal.
Nun mussten die Zahlen in die Spalten so eingesetzt werden, dass die geforderten Bedingungen erfüllt werden. Als erstes setzte Mag die 1 in Zelle 1a ein. Das Quadrat soll ein pandiagonales werden und das bedeutet, dass durch Versetzen von Spalten und/oder Zeile die 1 jede Position einnehmen kann, folglich auch die Zelle 1a.
Die 2 kann nicht in die 1. Zeile, 1. Spalte und fallende Diagonale eingesetzt werden, denn dann würden in diesen Reihen 2 Zahlen aus einem Block kommen. Es verbleiben in der 2. Zeile die Zellen 3b und 4b. Ein Einsatz in Zelle 4b ergab zwar ein magisches Quadrat, aber es war nicht pandiagonal. Damit verbleibt für die 2 nur Zelle 3b. Die 3 kann nur in Zelle 4c eingesetzt werden. Alle anderen Zellen befinden sich in Reihen, in denen bereits eine Zahl des 1. Blockes zu finden ist. Zwar befindet sich dabei die 3 mit der 2 in einer gebrochenen Diagonale, was jedoch nicht vermeidbar ist, denn Zeilen, Spalten und Hauptdiagonalen haben den Vorrang. Der 4 des 1. Blockes verbleibt nur noch die Zelle 2d. (Siehe Abb. 2)
Die 5, als 2. Zahl des Duos 4/5 und 1. Zahl des 2. Blockes, ist in die Zeile d einzusetzen. Die Zellen 1d und 4d scheiden aus, da in der Spalte 1 und der fallenden Diagonalen bereits die 1, als 1. Zahl des 1. Blockes eingetragen ist. Damit darf die 5 nur in die Zelle 3d eingesetzt werden. Auch die 6, als 2 Zahl des 2. Blockes kann nur in die Zelle 1c gesetzt werden, denn die Zelle 2c befindet sich in der steigenden Diagonale mit der 2 als 2. Zahl des 1. Blockes. Die 2 dominiert auch in der Spalte 3. Für die 7 verbleibt nur die Zelle 2b, denn in der Spalte 4 befindet sich bereits eine 3. Zahl. Für die 8 kommt nur noch die Zelle 4a in Frage, da die Spalten 1., 2. und 3, sowie den Zeilen b., c. und d bereits mit Zahlen des 2. Blockes belegt sind. (Siehe dazu Abb. 2.)
Als nächstes muss die 9 als 1. Zahl des 3. Blockes in die Zeile c eingeordnet werden. Von den noch freien 2 Zellen kommt nur die Zelle 2c in Frage, da sich in der Spalte 3 bereits die 5 als eine 1. Zahl befindet. Mit dem Einsatz der 9 lösen sich alle anderen Eintragungen. (Hoffentlich zum Guten!?)
Es sind einzusetzen:
Die 16 als 2. Zahl des Duos 9/16 in die einzig noch leere Zelle 3c.
Die 14 in Zelle 2a, damit die Summe 34 erreicht wird.
Die 11 als 2 Duozahl zur 14 in Zelle 3a.
Die 15 in Zelle 1d, damit die steigende Diagonale die Summe 34 hat.
Die 10 als 2. Duozahl in Zelle 4d und zum Schluss die beiden Duozahlen 12 und 13 so in Zeile b, dass die Spalten 1 und 4 jeweils die Summe 34 haben.
Abbildung 4 zeigt das so fertig gestellte Quadrat. Die Prüfung hat ergeben, dass es nicht nur magisch, sondern auch pandiagonal ist. Damit können Spalten und/oder Zeilen versetzt werden, wobei das Quadrat stets ein magisches und pandiagonales bleibt Leider bleibt es nicht immer so! Denn das Quadrat ist nur teilhomogen, da die Bedingungen in den gebrochenen Diagonalen nicht gesichert werden konnten. Die negativen Auswirkungen werden nachfolgend beschrieben.
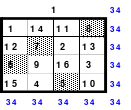
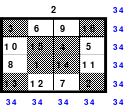
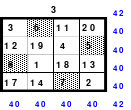
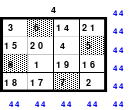
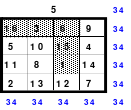
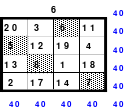
Das Quadrat 1 ist das gebildete Quadrat der 4. Ordnung. Die Zellen 5 bis 8 sind so eingeordnet, dass in jeder Zeile, Spalte und in den 2 Hauptdiagonalen je eine davon enthalten ist. Deshalb eignen sich diese besonders zum Zuschlagen eines Endrestes. Beim Quadrat 2 wurden die unteren 2 Zeilen nach oben versetzt und danach die 4. Spalte nach vorn. Das Quadrat ist magisch und pandiagonal geblieben. Beim 3. Quadrat wurden die Übergänge von Block zu Block unterschiedlich gewählt, und zwar von Block 1 zu Block 2 normal mit 1, von Block 2 zu Block 3 ist der Übergang 2 statt 1 und von Block 3 zu Block 4 = 3. Das Quadrat ist nicht mehr magisch und die Zellen 5 bis 8 sind so verteilt, dass keine davon in den Hauptdiagonalen zu finden ist und damit für den Zuschlag des Endrestes entfallen. Im 4. Quadrat wurde nur der Übergang von Block 2 zu Block 3 statt normal 1 mit 5 festgelegt. Das ist gleichzustellen mit der Zusammenfügung von Block 1 und 2 zu einem Block 1 und die Blöcke 3 und 4 werden zum Block 2. Das Ergebnis ist ein magisches und pandiagonales Quadrat bei dem lediglich die Einordnung der Zellen 5 bis 8 nicht wie gewünscht ist. Das Quadrat 5 wurde gebildet durch Versetzten der 2 oberen Zeilen nach unten und 2 Spalten von vorn nach hinten. Das Quadrat 6 wurde mit den gleichen Differenzen der Übergänge von Block zu Block wie beim Quadrat 3 gebildet. Das Ergebnis ist ein magisches, aber nicht mehr pandiagonales Quadrat, bei dem die Einordnung der Zellen 5 bis 8 den Forderungen entspricht.
Zusammenfassung der Erkenntnisse
Probleme können nur auftreten, wenn ein Endrest anfällt und das Basisquadrat durch Versetzen einer ungeraden Zahl von Zeilen und/oder Spalten verändert wird. Ein Endrest fällt nur bei Vorgabe einer ungeraden Zahl als magische Summe an, vorausgesetzt es wird die Duomethode angewendet. In diesem Fall kann der Vorführende keine Zelle bestimmen lassen, in die die erste Zahl eingesetzt werden soll, was ja nicht zwingend ist.
Alle anderen Abweichungen behindern die Berechnungen nicht.
Das gebildete Quadrat der 4. Ordnung kann als eines der Besten eingestuft werden, weshalb Mag es auch den Namen “Topquadrat” gegeben hat.
3.2.2. Das Semiquadrat
Bei der Suche nach der besten Lösung für ein Quadrat der 4. Ordnung hatte Mag verschiedene Wege zum Ziel verfolgt, wobei die meisten in einer Sackgasse endeten. Dabei war eine Lösung, die Mag erst später als brauchbar erkannte.
Es ist das Quadrat 1. Dieses Quadrat ist magisch mit der richtigen Summe von 34. Es ist ähnlich dem Topquadrat, denn gegenüber dem Topquadrat sind lediglich die letzten beiden Zahlen der Blöcke ausgetauscht. Das ist 3 mit 4, 7 mit 8, 11 mit 12 und 15 mit 16.
Die Analyse hatte 2 zu beachtenden Ergebnissen:
Jede 2. fallende Diagonale (grün) und jede 2. steigende Diagonale (weiß) hatten die magische Summe von 34.
In den Spalten betragen die Summen der 1. und 4. Zeile 17, die Hälfte der magischen Summe von 34. Gleiches trifft auf die Summen der 2. und 3. Zeile zu.
Mag nahm das Analyseergebnis zum Anlass ein Semiquadrat zu erstellen.
Als erstes versetzte er die obere Zeile nach unten und ein nur teilmagisches Semiquadrat war gefunden. Die Spaltensummen der 1. und 2. Zeile, sowie die 3. und 4. Zeile ist einheitlich 17. Alle Spalten und Zeilen haben die Summe 34, was leider nicht auf die Diagonalen zutrifft. (Quadrat 2)
Der Grund dafür ist klar. Zeigte doch die Analyse, dass nur jede 2. Diagonale die magische Summe von 34 hat. Bisher wurde ja nur eine Zeile verschoben. Es musste nur noch eine Zeile oder Spalte versetzt werden und das Quadrat ist wieder magisch. Eine weitere Zeile ist nicht möglich, denn dann würde die semimagische Ordnung aufgehoben. Mag versetzte die 1. Spalte nach hinten und das semimagische Quadrat war fertig. (Quadrat 3)
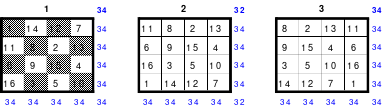
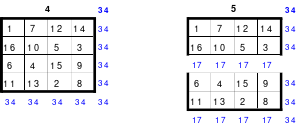
Zum Schluss schönte Mag das gefundene Quadrat durch Wenden um die senkrechte und waagerechte Achse. (Quadrat 4)
Mag gab diesem teilbaren Quadrat den Namen “Semiquadrat” und nahm es in seine Sammlung auf. (Quadrat 5). Das Semiquadrat ist homogen und pendelbar.
Sicher kann die Frage nach dem Sinn eines solchen Quadrates gestellt werden. Es wird sehr wahrscheinlich selten zum Einsatz kommen, kann aber im Bedarfsfall sehr nützlich sein. Mag verweist in diesem Zusammenhang auf das Kombiquadrat “Ein Verbundquadrat” in der Datei “Ausgewählte Kombiquadrate”, die im “Anhang” zu finden ist.
Bei der Bildung dieses Kombiquadrates kam das Semiquadrat zur Anwendung. Sicher wäre auch eine Lösung ohne das Semiquadrat erreicht worden, aber mit einem weitaus höheren Aufwand. Da dort keine weiteren Erläuterungen zum Semiquadrat enthalten sind, hat Mag diese hier in seine Ausführungen aufgenommen.
3.2.3. Die Fusionsmethode
Nur bei der Universalmethode war es möglich, auch einfachgerade magische Quadrate wie das 6er, 10er, 14er usw. zu konstruieren. Dabei ist die Qualität dieser Quadrate nicht gerade hoch. Um diesen Nachteil zu beheben hat Mag die Fusionsmethode entwickelt. Bei der Fusionsmethode werden mehrere kleinere Quadrate zu einem größeren verschmolzen. Dabei müssen die kleinen Quadrate keine magischen sein. Selbst die kleinsten Folgequadrate, die 2 x 2 = 4 Zellen großen Quadrate, in denen nach einer bestimmten Ordnung die Zahlen fortlaufend eingesetzt werden, können Verwendung finden. Die dabei entstehenden größeren Quadrate sind natürlich nicht magisch. Aber wie bei der Universalmethode werden Teile der Spalten und Zeilen so versetzt, dass ein magisches Quadrat entsteht. Der Vorteil dabei besteht in der größeren Variabilität um zumindest ein teilhomogenes Quadrat zu erreichen. Als erstes zeigt Mag die Bildung von einfachgeraden Quadraten.
Einfach gerade Fusionsquadrate
Das Hexaquadrat
Um das nicht magische Ausgangsquadrat zu bilden wurden auf der Grundlage des abgebildeten 2er Folgequadrat (Quattro) 9 Wechselquadrate gebildet, die dann nach der Ordnung des Miniquadrates zusammengesetzt wurden. Das so entstandene Quadrat ist das Quadrat Nr. 1. Es ist nicht magisch, denn die Zeilen und Spalten haben nicht die magische Summe von 111. Lediglich die Diagonalen haben diesen Wert, was in der Anwendung von Folgequadraten begründet ist. Auffallend ist, dass die Spalten eine Summe von 84 und 138 haben, deren Mittelwert 111 ist. Die Differenzen zu 111 sind einmal +27 und einmal -27. Die Zahlen der 1., 3 und 5. Spalte sind jeweils um 9 kleiner als die 2., 4. und 6. Spalte. Durch den Tausch von jeweils 3 Zahlen würde ein Ausgleich von +/-27 erreicht. Der Tausch wird dabei so gewählt, dass von den 6 großen Zahlen 31 bis 36 je eine in eine Spalte kommt. Im Quadrat 1 sind die großen Zahlen durch Fettdruck hervorgehoben. Das Quadrat 2 zeigt eine Lösung. Die zu tauschenden Zahlen sind blau gekennzeichnet und müssen um die verstärkt dargestellten Achsen gedreht werden.
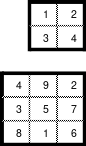
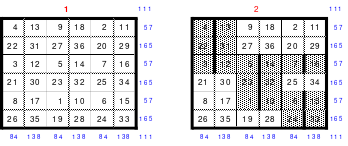
Das Ergebnis, ein Zwischenergebnis, ist das Quadrat Nr. 3. Alle Spalten haben den richtigen Summenwert von 111. In jeder Spalte befindet sich eine der Zahlen von 31 bis 36. Wichtig bei der Auswahl der auszutauschenden Zahlen ist, dass stets ein Ausgleich der Diagonalen erreicht wird. Die Anzahl der aus den Diagonalen gedrehten Zahlen muss der Anzahl der hinein gedrehten Zahlen entsprechen.
Bei den Zeilen ist die Situation die Gleiche. Hier sind die Summen 57 und 165, das sind +54 und -54 zum Mittelwert 111. Die Differenzen zwischen den Zahlen beträgt 18 und 3 x 18 ist 54. Demzufolge sind auch hier jeweils 3 benachbarte Zahlen zwischen der 1. und der 2., 3. und 4., sowie 5. und 6. Zeile zu tauschen.
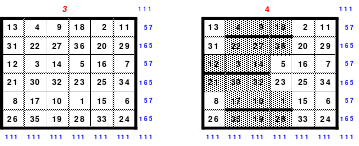
Im 4. Quadrat sind die zum Tausch vorgesehenen Zahlen als Vorschlag rot gekennzeichnet. Das Wenden erfolgt hier ebenfalls um die verstärkt gezeichneten Achsen. Die Auswahl kann nicht beliebig erfolgen. So muss auch hier gesichert werden, dass in jede Zeile eine der großen Zahlen kommt und die Diagonalen ihren Wert behalten. Zusätzlich erfolgte die Auswahl so, dass nur in einer Diagonalen eine der beiden größten Zahlen, 35 oder 36 zu finden ist. Dies ist Voraussetzung, um durch Pendeln unter Einbeziehung eines 6er Alternativquadrat ein 18er Monoquadrat zu bilden. Näheres dazu finden Sie im Abschnitt “Monoquadrate”.
Das Ergebnis dieses Tausches ist das folgende
Hexaquadrat
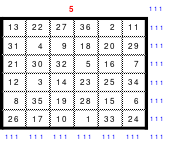
Das Hexaquadrat enthält in jeder Zeile, Spalte und Diagonalen je eine der Zahlen von 31 bis 36, wobei in der fallenden Diagonale die zweitgrößte Zahl, die 35 zu finden ist. Damit ist es zwar nur teilhomogen, eignet sich dadurch auch zur Bildung eines 6er Multiquadrates. In jeder Reihe sind 3 gerade und 3 ungerade Zahlen enthalten wodurch es pendelbar ist. Des Weiteren sind in jeder Reihe 3 Zahlen kleiner 19 und 3 Zahlen größer 18 vorhanden. Damit ist es auch distributiv, was für den Einsatz bei Rahmenquadraten (siehe dort) vorteilhaft ist, da alle Optionen genutzt werden können.
Aufgrund der aufgezeigten Eigenschaften betrachtet Mag dieses Quadrat als das beste unter den 6er Quadraten, weshalb Mag es auch mit den Namen “Hexaquadrat” hervorhebt.
Mag hatte bereits erwähnt, dass zur Bildung eines 18er Homogenquadrat ein 6er Alternativquadrat erforderlich ist. Dieses kann durch das Wenden anderer Zahlen erreicht werden, wobei auch hier die Auswahl der Zahlen so erfolgt, dass die Diagonalen Summen erhalten bleiben und in jeder Reihe ebenfalls eine große Zahl zu finden ist. Das 6. Quadrat zeigt ein Beispiel dazu. Das Wenden der Spalten wurde wie vorher durchgeführt und nur eine andere Auswahl zum Wenden der Zeilenzahlen genutzt. Der Unterschied zum Hexaquadrat besteht darin, dass in den beiden Diagonalen keine der 2 größten Zahlen, 35 oder 36, enthalten ist.
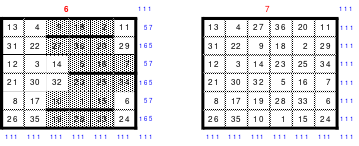
Das 6er Alternativquadrat
In dieser Form können alle einfachgeraden Quadrate gebildet werden. Als nächstes zeigt Mag die Entstehung des Dekaquadrat.
Das Dekaquadrat
Wie das Hexaquadrat, erfolgt auch die Bildung des 10er Dekaquadrates. Als erstes wurden 25 Wechselquatros gebildet und entsprechend dem perfekten 5er Primquadrat, dem Pentaquadrat, eingeordnet. Aus Vorteilsgründen wurde aber die 5. Zeile des sekundären Pentaquadrat nach oben versetzt. Das Ergebnis zeigt das folgende Quadrat
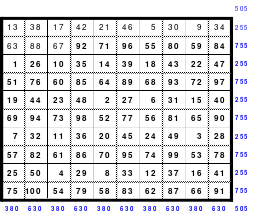
Der weitere Ablauf erfolgt wie beim Hexaquadrat, nur dass hier die Differenzen andere sind. So haben auch hier nur die Diagonalen die richtige magische Summe von 505. Die Spalten weichen davon mit +/-125 ab. Die benachbarten Zahlen in der Waagerechten haben eine Differenz von 25. Somit müssen 5 Zahlenpaare getauscht werden. Der Tausch muss auch hier so erfolgen, dass in jede Spalte eine der großen Zahlen von 91 bis 100 kommt. Die großen Zahlen sind durch Fettdruck hervorgehoben. Auch die Summenerhaltung der Diagonalen ist sicher zu stellen. Der Tauschvorschlag ist im folgenden Quadrat blau gekennzeichnet.
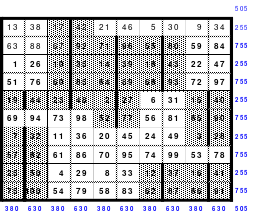
Der erfolgte Zahlentausch ist im nächsten Quadrat ersichtlich. Alle Spalten haben als Summe den richtigen Wert von 505. Auch die Verteilung der großen Zahlen erfolgte so, dass in jeder Spalte eine enthalten ist. Die Summen der Diagonalen haben sich nicht verändert.
Nun sind die Zeilen zu bereinigen. Hier betragen die Differenzen der Zeilensummen +/- 250, das ist 5 x 50 und 50 ist die Differenz der benachbarten Zahlenpaare. Folglich sind jeweils 5 Zahlenpaare um die hervorgehobenen Achsen zu wenden. Dabei muss wieder beachtet werden, dass in jede Zeile einer der großen Zahlen kommt, wobei in eine Diagonale die 100 kommen soll. Eine mögliche Variante zur Erreichung dieses Zieles ist rot hinterlegt worden.
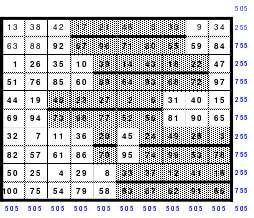
Nach erfolgtem Tausch ist ein magisches Quadrat der 10. Ordnung entstanden, das Mag das “Dekaquadrat” nennt.
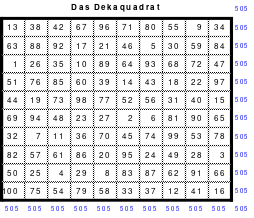
Das Dekaquadrat ist pendelbar, distributiv und teilhomogen und kann damit zur Bildung von Multiquadraten und zur Bildung größerer Quadrate der 10er Reihe durch Pendeln eingesetzt werden. Beim Einsatz in Rahmenquadrate können alle Optionen genutzt werden.
Das 14er Fusionsquadrat
Das nächst größer einfachgerade Quadrat ist das 14er.
Dieses wird wie die anderen gebildet. Als Primärquadrat kommt wieder das 2 x 2 große Folgequadrat und als Sekundärquadrat das 7er Primquadrat, das Heptaquadrat, zum Einsatz. Das Folgequattro wird 7 x 7 = 49 mal als Wechselquadrat ausgebildet und in das Heptaquadrat eingeordnet.
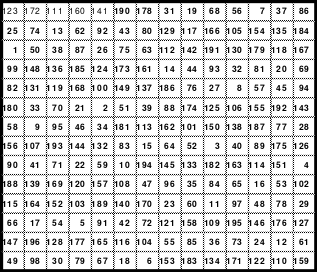
Das 14er Fusionsquadrat
Dann folgt das Wenden wie bei den beiden vorangegangenen Quadraten. Mag erspart sich diesmal jedoch jeden Kommentar. Er ist sich sicher, dass Sie die Entstehung selbst nachvollziehen können. Das Ergebnis seiner Arbeit will er aber Ihnen nicht vorenthalten.
Das 14er Fusionsquadrat verfügt über alle Eigenschaften wie das Hexa- und Dekaquadrat. Es ist Pendelbar, teilhomogen und distributiv. Das nächste einfachgerade Quadrat ist das 18er, dass in gleicher Weise gebildet werden kann. Mag wird aber ein 18er Quadrat im Abschnitt “Monoquadrate” vorstellen. Es wird durch das 3 * 3 = 9-fache Pendeln des Sextaquadrates erstellt.
Damit schließt Mag die Bildung einfachgerader Fusionsquadrate ab und zeigt, dass auch die Bildung mehrfachgerader und ungerader Fusionsquadrate möglich ist.
Mehrfachgerade Fusionsquadrate
Ein 4er Fusionsquadrat
Ausgang ist wieder das Folgequattro, das 4-fach als Wechselquadrat gebildet wird und wie das Folgequattro eingeordnet. Quadrat 1 zeigt das Ausgangsquadrat. Der Ausgleich wird in diesem Fall analog vorgenommen, wobei jeweils 2 Zahlen der äußeren Spalten und der inneren getauscht werden. Die blauen Markierungen zeigen ein Beispiel. Nach erfolgtem Tausch haben alle Spalten die richtige Summe von 34, was aus Quadrat 2 zu entnehmen ist. Im Quadrat 2 ist nach gleicher Struktur der Tausch zwischen den Zeilen dargestellt. Das Ergebnis ist das Quadrat 3. Leider zeigt dieses Quadrat einen Mangel. In der fallenden Diagonale befinden sich 2 Zahlen aus dem Block der großen Zahlen 13 bis 16 und in der steigenden ist keine dieser Zahlen zu finden. Da es sich um ein assoziatives Quadrat handelt, ist der Tausch der 2. mit der 3. Zeile ohne weiteres möglich. Das 4. Quadrat ist das Endprodukt, ein assoziatives, pendelbares, distributives sowie homogenes und damit ein hochwertiges magisches Quadrat. Es kann fast auf die gleiche Stufe mit den vollkommenen Quadraten gestellt werden. Leider nur fast.
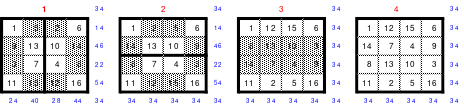
Der wesentliche Nachteil besteht darin, dass nicht einzelnen Spalten und/oder Zeilen versetzt werden können, sondern nur immer 2. Dafür können diese aber nach den Regeln assoziativer Quadrate auch getauscht werden. Wird nur eine Reihe versetzt, so ist das Quadrat nicht mehr homogen und die Diagonalen haben nicht die magische Summe womit das Quadrat kein magisches mehr ist.
Nachfolgen einige Beispiele des Versetzens oder Tauschens von jeweils 2 Reihen.
Das 1. Quadrat entstand durch das Versetzen der ersten beiden Spalten nach hinten. Beim 2. Quadrat wurde die 1. Zeile nach unten und anschließend die 1. Spalte nach hinten versetzt. Im 3. Quadrat wurden 2 Spalten und 2 Zeilen versetzt. Die
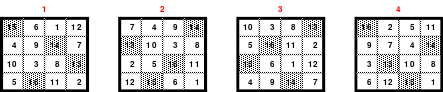
Die Möglichkeiten, die ein assoziatives Quadrat bieten wurden im 4. Quadrat genutzt. Hier erfolgte der Tausch der 1. mit der 4. Zeile und der 1. mit der 4. Spalte. Alle diese Varianten sind magische Quadrate und haben ihre Eigenschaften behalten. Lediglich das 2. ist nicht mehr assoziativ.
Das Oktaquadrat
Auch ein Quadrat der 8. Ordnung kann als Fusionsquadrat gebildet werden.
Das Ausgangsquadrat sind 16 Wechselquadrate aus dem Folgequattro die in das Topquadrat eingeordnet wurden.
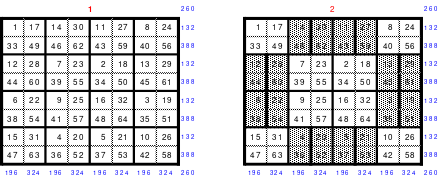
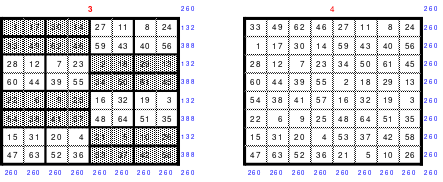
Das Oktaquadrat
Die Quadrate 1 bis 4 zeigen den Werdegang. Einzelheiten müssen nicht erläutert werden.
Das so entwickelte Quadrat ist homogen, distributiv und pendelbar. Es kann nicht wie ein 8er Pendelquadrat in 4 magische Teilquadrate untergliedert werden. Es können wie beim 4er Fusionsquadrat jeweils nur eine gerade Anzahl von Reihen versetzt werden. Da es jedoch nicht assoziativ ist, können keine Reihen getauscht werden.
Aufgrund der Qualität dieses 8er Quadrates, das wie ein Soloquadrat wirkt, hat Mag es “Oktaquadrat” getauft.
Ungerade Fusionsquadrate
Die Bildung ungerader Fusionsquadrate ist wesentlich schwieriger als gerade. Sie haben allerdings auch den Vorteil, dass zumindest eine Teilhomogenität leicht erreicht werden kann. Mag wird als Beispiel ein 9er Fusionsquadrat erstellen.
Ein 9er Fusionsquadrat
Da ein 9er Quadrat ein ungerades ist, kann das primäre Folgequadrat auch nur ein ungerades sein, ein 3 x 3 großes, das links abgebildet ist. 3 ist nämlich die einzige Zahl durch die die 9 geteilt werden kann. Dieses Folgequadrat ist Basis für 9 Wechselquadrate, die kleinen Quadrate von 1 bis 9.
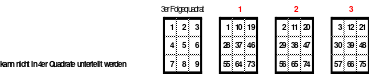
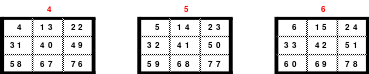
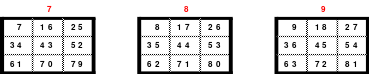
Diese Wechselquadrate wurden im großen Quadrat Nr. 1 entsprechend der Ordnung des Miniquadrates eingesetzt.
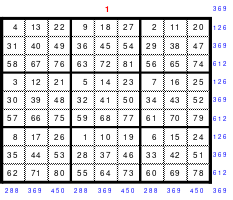
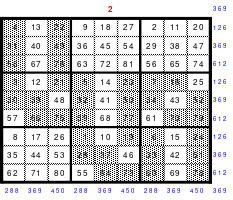
Die Diagonalen haben als magische Summe den richtigen Wert von 369. Auch die mittleren Spalten und Zeilen der 3er Blöcke haben diesen Wert. Die 1. Spalten der 3er Blöcke haben einheitlich als Summe 288 und die 3. Spalten 450. Die Differenzen zu 369 sind +/-81. Die Differenzen zwischen den einzelnen Zahlen der 1. und 3. Spalte ist einheitlich 18. Folglich sind 81: 18 = 4,5 Zahlenpaare zu tauschen. Wie das geht, wurde bei der Bildung ungerader Universalquadrate beschrieben. Es sind demzufolge 4 Zahlenpaare der 1. und 3. Spalte zu tauschen, sowie je 1 Zahlenpaar der 1. mit der 2. und der 3. mit der 2. Das Quadrat 2 zeigt eine Lösung (blaue Markierung).
Wichtig ist dabei, dass bei den Diagonalen entweder alle 3 Zahlenpaare der 1. und 3. Spalte getauscht werden, oder keinerlei Tausch vorgenommen wird. Das ist notwendig zur Erhaltung der Diagonalen. Weiter ist wichtig, dass beim Tauschen die großen Zahlen 73 bis 81 so verteilt werden, dass je eine in jede Spalte kommt. Das Quadrat 3 beinhaltet den Tausch, wodurch gleiche magische Summen von 369 für alle Spalten erreicht wurden.
So wie die Spalten sind nun die Zeilen zu korrigieren. Die Differenzen sind hier +/- 243 und 54, demzufolge auch hier jeweils 4,5 Zeilen zu tauschen sind. Das ist aber nur bei den ersten und dritten 3 Zeilen leicht lösbar. Die Einbeziehung der Eckquadrate ganz oder nicht kann nicht eingehalten werden. Aber die Diagonalen wurden belassen, wodurch keine Veränderung der magischen Summen eintritt. Auch hier wurden die Tauschpaare so gewählt, dass die großen Zahlen in jede Zeile kommen. Bei den mittleren 3 Zeilen war es nicht möglich 4,5 Zeilen zu tauschen. Es standen nur die 3 Zahlenpaare des mittleren Quadrates zur Verfügung, wodurch ein Ausgleich von 162 erfolgte und ein Rest von 81 verblieb. Dieser Rest konnte durch den jeweils halben Tausch der Zahlen 16 mit 52, 34 mit 70, 3 mit 48 und 30 mit 75 bereinigt werden. Im 3. Quadrat sind die zu tauschenden Zahlen rot gekennzeichnet.
Nach diesem Tausch war das 9er Fusionsquadrat, ein teilhomogenes Quadrat mit der magischen Summe von 369 in allen Reihen entstanden. Es ist das 4. Quadrat.
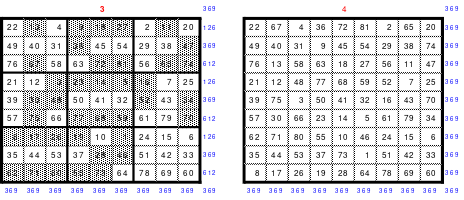
Mag schließt die Erläuterungen zu den Fusionsquadraten mit dem Hinweis ab, dass auf der Grundlage der gezeigten Beispiele noch weitere einfachgerade, mehrfachgerade und ungerade Quadrate mit dieser Methode gebildet werden können. Sicher finden Sie dazu Lösungen, zumal mit der zunehmenden Größe der Quadrate der Tausch der Zahlenpaare leichter wird, wie es auch bei der Universalmethode der Fall ist. Das wichtigste Ergebnis aus diesen konstruktiven Darlegungen ist die vorteilhafte Möglichkeit zur Bildung einfachgerader Quadrate.
Eine Nachbetrachtung
In den Beispielen wurde angestrebt, dass in jeder Reihe des Quadrates eine Zahl des letzten Blockes enthalten ist. Das ist erforderlich, um im Hexen 1x1 diese um einen eventuellen Endrest zu erhöhen. Soll das Quadrat nicht im Hexen 1x1 eingesetzt werden, kann auf diese Regel verzichtet werden und das Wenden der Quattros kann frei erfolgen.
Dies gilt auch für die Wendemethode.
3.2.4. Die Wendemethode
Bei der Analyse des Dürerquadrates fiel Mag auf, dass sich sowohl die kleinsten Zahlen, 1 bis 4, als auch die größten, 13 bis 16 zu je 2 auf den beiden äußeren Zeilen befinden. Ähnlich ist es mit den beiden anderen Blöcken 5 bis 8 und 9 bis 12. Die Einordnung dieser Zahlen lässt erkennen, dass eine Drehung der äußeren Spalten um die waagerechte Achse dazu führt, dass sich die Zahlen eines Blockes jeweils in einer Zeile befinden.
Das linke Quadrat ist das Dürerquadrat. Dreht man die blau markierten Spalten um die waagerechte Achse, so entsteht das mittlere Quadrat. Bei den grünen Zellen sind die Zahlen von rechts nach links eingeordnet und die roten von links nach rechts, wobei sich die Zahlen des 2. Blockes in der 3. und die des 3. Blockes in der 2. Zeile befinden. Werden die grünen Zeilen um die senkrechte und die roten um die waagerechte Achse gewendet, so entsteht das rechte Quadrat. Es ist ein 4er Folgequadrat.
Umgekehrt müsste es nun möglich sein, aus Folgequadraten andere, auch größere Quadrate zu bilden. Zuerst aber soll ein 4er Quadrat gebildet werden.
Links das Folgequadrat mit den um die senkrechte Achse zu wendenden, blauen Zeilen. In der Mitte ist der zweite Schritt, das Wenden der Spalten um die waagerechte Achse zu sehen. Ganz rechts das fertige 4er Quadrat. Es ist wie das Dürerquadrat ein assoziatives, distributives und pendelbares Quadrat.
In gleicher Weise können auch größere, mehrfach gerade magische Quadrate gebildet werden. Mag führt dazu den Beweis durch die Bildung eines Quadrates der 8. Ordnung.
Links ist ein 8er Folgequadrat abgebildet. In diesem sind die Zahlen 1 bis 64 in ihrer natürlichen Folge eingesetzt. Werden anschließend die blau markierten Spalten um die waagerechte Achse gewendet, so entsteht das rechte Quadrat.
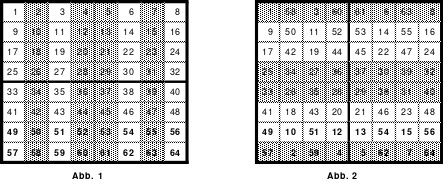
Werden in diesem nun die grün gekennzeichneten Zeilen um die senkrechte Achse gewendet, so ist das Ergebnis das unten abgebildete magische Quadrat der 8. Ordnung mit der magischen Summe von 260. Dieses Quadrat ist ein assoziatives. Alle symmetrisch zum Mittelpunkt befindlichen Zahlenpaare haben einheitlich 65 als Summe. Als Beispiel sind einige assoziative Zahlenpaare farblich kenntlich gemacht. Es sind 63 + 2 = 65 (grün), 52 + 13 = 65 (rot) usw.
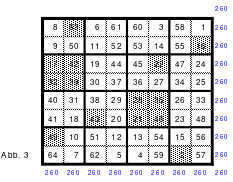
Des Weiteren ist dieses Quadrat pendelbar, assoziativ und distributiv, denn in jeder Reihe befinden sich je 4 gerade und 4 ungerade Zahlen und auch die kleinen Zahlen 1 bis 32 und die großen 35 bis 64 sind mit jeweils 4 in jeder Reihe vorhanden. Es ist jedoch nicht homogen oder teilhomogen und ist damit für das Hexeneinmaleins ungeeignet. Darüber hinaus weist das Quadrat noch eine Besonderheit aus. Unterteilt man das Quadrat in 4 x 4 = 16 Quattros, so ist die Quadratsumme jedes einzelnen Quattro einheitlich 130. (Siehe gelbe Markierung als Beispiel)
Auf eine Gesetzmäßigkeit muss unbedingt aufmerksam gemacht werden. Ein magisches Quadrat entsteht nur, wenn die Spalten und Zeilen, die gewendet werden sollen, symmetrisch zu den Mittelachsen angeordnet werden. In der linken Hälfte des Quadrates nach Abb. 1 sind dies die Spalten 2 und 4 und in der rechten Hälfte sind es die Spalten 5 und 7. Sie befinden sich symmetrisch zur senkrechten Achse. Bei den Zeilen ist es ebenso. Hier wurden die Zeilen 1, 4, 5, und 8 gewählt. Auch diese befinden sich mit je 2 in einer Hälfte und sind symmetrisch zur waagerechten Achse ausgerichtet. Wird diese Gesetzmäßigkeit nicht beachtet, so entsteht kein magisches Quadrat. Zwar werden die Zeilen und Spalten die magische Summe haben, nicht aber die Diagonalen.
Daraus muss aber auch abgeleitet werden, dass nach dieser Variante keine einfach geraden oder ungeraden Quadrate gebildet werden können. Zum Beispiel wären in einem 6er Quadrat 3 Zeilen und 3 Spalten zu wenden. Diese können aber nicht zu gleichen Teilen in die linke und rechte Hälfte des Quadrates eingeordnet werden und eine symmetrische Einordnung ist genauso unmöglich. Bei ungeraden Quadraten trifft dies ebenso zu.
4 Kombiquadrate
4.1 Methoden zur Bildung von Kombiquadraten
Kombiquadrate entstehen durch die Kombination mehrerer Quadrate zu einem Quadrat. Dabei werden mehrere Teilquadrate unter Beachtung der Struktur eines magischen Quadrates gebildet und in der Regel entsprechend der Struktur eines weiteren magischen Quadrates zusammengefügt. Das magische Quadrat nach dessen Struktur die Teilquadrate gebildet werden nennt Mag das “Primärquadrat”. Als “Sekundärquadrat” bezeichnet er das magische Quadrat entsprechen dem die Teilquadrate zu einem magischen Quadrat zusammengesetzt werden. In der Regel sind die gebildeten Teilquadrate magisch und enthalten lückenlos alle Zahlen von 1 bis n. Das Primärquadrat muss ein magisches sein. Natürlich können Primär- und Sekundärquadrat auch ein gleiches Basisquadrat haben.
Ein Sonderfall sind gerade Pendelquadrate und ungerade Korrekturquadrate. Da hier die gebildeten Teilquadrate gleiche magische Summen haben, ist deren Zusammensetzung nicht an ein magisches Quadrat gebunden. Hier können z. B. aus 4 gependelten Teilquadraten der 6. Ordnung ein Quadrat der 12. Ordnung gebildet werden. Mit ungeraden Korrekturquadraten können dagegen nur ungerade größere Quadrate gebildet werden.
Weitere Fragen werden in den folgenden Abhandlungen geklärt.
Im Wesentlichen können die Kombiquadrate nach 3 verschiedenen Varianten gebildet werden:
Die gebundenen Kombiquadrate
Sie werden aus geraden und ungeraden Quadraten mit gleicher Ordnungszahl,
jedoch mit unterschiedlichen magischen Summen zusammengesetzt. Die Differenzen zwischen den magischen Summen müssen jedoch gleichgroß sein. Die dafür geeigneten Quadrate können als Primärquadrate mittels der Reihen - oder Wechselmethode gebildet werden. Die Zusammensetzung dieser Quadrate ist an ein als Sekundärquadrat bezeichnetes magisches Quadrat gebunden.
Ungebundene Kombiquadrate.
Die ungebundenen Kombiquadrate werden durch das Zusammenfügen von Quadraten mit gleicher Ordnungszahl und gleichen magischen Summen gebildet. Da alle Teilquadrate die gleichen magischen Summen haben, ist das Zusammenfügen nicht an eine Ordnung gebunden und es ist kein Sekundärquadrat erforderlich. Die hierfür geeigneten Methoden zur Bildung der Teilquadrate ist die Pendel- und Korrekturmethode. Mittels der Pendelmethode können nur gerade Kombiquadrate gebildet werden und mittels der Korrekturmethode nur ungerade Kombiquadrate.
Ausgewählte Kombiquadrate, (die Mag auch als Konglomerate bezeichnet.)
Bei diesen Quadraten und Gebilden kommen neben Teilquadraten mit zum Teil unterschiedlichen Ordnungszahlen und unterschiedlichen magischen Summen auch weitere Formen, wie Rahmen, Winkel und Semiquadrate zum Einsatz. Die Bildung solcher Konglomerate erfordert meistens ein gutes Wissen zu den magischen Quadraten und entsprechende kreative Fähigkeiten.
Mag verzichtet deshalb in seinen Ausführungen größere Abhandlungen zu diesem Thema zu machen, verweist aber auf die Datei “Ausgewählte Kombiquadrate”, die in der Anlage enthalten ist und einige Beispiele ausgewählter Kombiquadrate, magischer Gebilde und Kurioses mit Erläuterungen dazu enthält.
Die genannten Methoden: Reihen-, Wechsel, Pendel- und Korrekturmethode werden in den nachfolgenden Dateien näher beschrieben und Beispiele zur Bildung von Kombiquadraten erläutert.
4.2 Die Reihenmethode
Bei der Reihenmethode werden die Zahlen der Reihe nach sowohl in die Teilquadrate, als auch von Teilquadrat zu Teilquadrat entsprechen der natürlichen Zahlenreihe eingetragen. Nachstehen werden 3 Teilquadrate der 4. Ordnung gezeigt, in die die Zahlen von 1 bis 48 der Reihe nach eingetragen wurden. Begonnen wurde mit dem Teilquadrat 1, in das die Zahlen von 1 bis 16 eingesetzt wurden. In das Teilquadrat 2 kamen die Zahlen 17 bis 32 und in das Teilquadrat 3 die Zahlen von 33 bis 48.
Die Einordnung der Zahlen erfolgte nach dem Dürerquadrat, das als Primärquadrat gewählt wurde. Alle 3 Quadrate sind magisch, assoziativ, kommutativ, distributiv und pendelbar, genau wie das unveränderte Dürerquadrat. Das bedeutet, dass die Eigenschaften des Primärquadrates auf die nach der Reihenmethode gebildeten Teilquadrate übertragen werden.
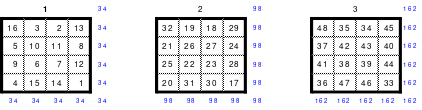
Alle Zahlen im 2. Teilquadrat sind um 16 größer als im 1., und im 3. Teilquadrat um 32 größer als im 1. Daraus kann für die Berechnung eines Teilquadrates nach der Reihenmethode folgende Formel abgeleitet werden.
Zn = Za + (Tn - 1) * A
Darin bedeuten: Zn = neue Zellenzahl
Za = alte Zellenzahl, bzw. die Zellenzahl des Ausgangsquadrates
Tn = das aktuelle Teilquadrat
A = Anzahl der Zellen je Quadrat
Danach würde z. B. die neue Zellenzahl für die Zelle16 im 3. Teilquadrat
Z3 = 16 + (3 - 1) x 16 = 48 sein.
Natürlich muss nicht jede neue Zellenzahl berechnet werden. Es genügt auch nur die Zahl für die 1. Zelle zu berechnen und alle anderen Zahlen in ihrer Folge einzusetzen.
Hervorzuheben sind die stark unterschiedlichen magischen Summen in den Größen von 34, 98 und 162. Auch aus diesen magischen Summen kann eine Formel zur Berechnung der magischen Summe eines beliebigen Teilquadrates abgeleitet werden.
mSn = (a2 + 1) / 2 * a +a3 * (Tn -1)
Darin bedeuten: mSn = magische Summe des n-ten Teilquadrates (Tn)
a = Anzahl der Zellen je Reihe (entspr. der Ordnungszahl)
Danach ist die magische Summe für das 3. Teilquadrat:
mS3 = (4² + 1) / 2 x 4 + 4³ *(3-1) = 162
Doch nun zur praktischen Anwendung.
Als erstes soll ein 12er Quadrat entstehen. Als Primärquadrat soll das Miniquadrat und als Sekundärquadrat ein 5er Diagonalquadrat zum Einsatz kommen. Damit will Mag auch zeigen, dass es völlig egal ist welche Quadrate zur Anwendung kommen. Wichtig ist in diesem Fall nur, dass es sich um magische Quadrate handelt.
Links ist das Miniquadrat abgebildet. Es wurde als Primärquadrat gewählt. Das 5er Diagonalquadrat, das rechts abgebildet ist, wurde als Sekundärquadrat gewählt.
Nach der Bildung von 25 Teilquadraten nach der Reihenmethode wurden diese nach der Ordnung des 5er Diagonalquadrates zusammengefügt. So entstand das untere magische Quadrat der 15. Ordnung. Es ist wie das Miniquadrat und auch das 15er Quadrat assoziativ. Die magische Summe ist 1695.
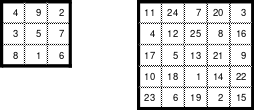
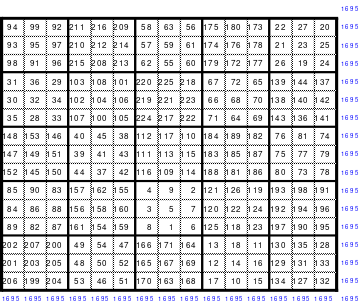
In die Zelle 1 des 5er Quadrates wurde das Teilquadrat mit den Zahlen von 1 bis 9 eingesetzt. In die 2. Zelle das Quadrat mit den Zahlen von 10 bis 19. So wird ein Teilquadrat nach dem anderen eingeordnet. Zuletzt wird in die Zelle 25 das Teilquadrat mit den Zahlen von 217 bis 225 eingefügt und das nach der Reihenmethode gebildete magische Quadrat mit der richtigen magischen Summe von 1695 ist fertig.
Nach dieser Methode können weitere große Quadrate gebildet werden. Die mögliche Größe ergibt sich aus dem Produkt der Ordnungszahlen von Primär- und Sekundärquadrat. Als kleinstes Reihenquadrat kommt ein 9er Quadrat in Frage, das aus 9 Teilquadraten besteht. Primär- und Sekundärquadrat sind jeweils das Miniquadrat.
Weitere mögliche Größen von Kombiquadraten sind:
12er: aus Mini- und 4er Quadrat (3 x 4 = 12)
15er: aus Mini- und 5er Quadrat (3 x 5 = 15)
16er: aus 2-mal 4er Quadrat (4 x 4 = 16)
18er: aus Mini- und 6er Quadrat (3 x 6 = 18)
20er: aus 4er - und 5er Quadrat (4 x 5 = 20)
21er: aus Mini und 7er Quadrat (3 x 7 = 21)
24er: aus 4er - und 6er Quadrat (4 x 6 = 24) usw. usw.
Die Reihenquadrate sind nicht gerade attraktiv und die Methode der Bildung ist leicht zu erkennen. Das trifft auch auf das folgende 12er Quadrat zu, das aus dem Toppquadrat als Primärquadrat und dem Miniquadrat als Sekundärquadrat besteht.
Die magische Summe ist 870.
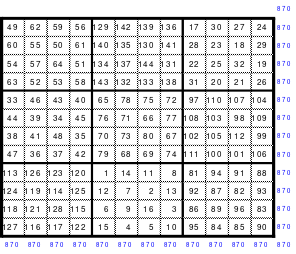
Eine wesentlich bessere Zahlenverteilung wird bei der Wechselmethode erreicht, die der Reihenmethode sehr ähnlich ist. Die Wechselmethode wird als nächstes beschrieben.
(Eine günstigere, weniger auffällige Struktur wird auch durch die Umgestaltung zum Chaosquadrat erreicht. Dazu erfolgen aber später im Abschnitt Chaosquadrate Angaben.)
4.3. Die Wechselmethode
Die Wechselmethode ermöglicht die Erstellung von mehreren magischen Quadraten bei Einsatz der ununterbrochenen Zahlenfolge von 1 bis n, ähnlich der Reihenmethode. Bei der Wechselmethode wird jedoch nicht erst ein ganzes Quadrat mit Zahlen ausgefüllt, ehe es zum nächsten Quadrat geht, sondern es wird in jedes Quadrat immer nur eine Zahl eingesetzt und dann zum nächsten Quadrat gewechselt. Ist eine Zahl im letzten Quadrat eingeschrieben, so wird wieder beim ersten Quadrat begonnen. Die abgebildeten 3 Teilquadrate zeigen den Ablauf näher. Das Ausgangsquadrat ist das Topquadrat. Zuerst werden die Zahlen 1 bis 3 in die Zelle 1 der 3 Teilquadrate eingetragen. Dann folgen die Zahlen 4 bis 6, die in die Zelle 2 eingesetzt werden. Die Zahlen 7 bis 9 kommen in die Zelle 3 usw. und zum Schluss die Zahlen 46 bis 48 in die Zell 16 der Quadrate 1, 2 und 3. Die fertigen 3 Teilquadrate haben die magischen Summen 94, 98 und 102. Die Differenzen derselben sind gegenüber der Reihenmethode sehr gering.
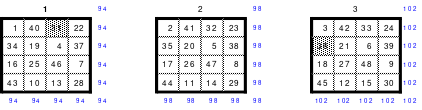
Die Anordnung der Zahlen ermöglicht es auch hier eine mathematische Interpretation in der Formel.
Ausgangsquadrat 
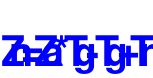
Darin bedeuten: Zn = die neue Zellenzahl
Za = die Zellenzahl im Ausgangsquadrat
Tg = Anzahl der Teilquadrate insgesamt
Tn = das aktuell zu berechnende Teilquadrat
Nachfolgend werden Beispiele zur Anwendung der Formel bei Bildung der obigen 3 Teilquadrate der 4. Ordnung gezeigt.
Berechnung der neuen Zellenzahl für die
Zelle 11 des 1. Teilquadrat (blau): Zn = 11 x 3 - 3 + 1 = 31
Zelle 12 des 3. Teilquadrates (grün): Zn = 12 x 3 - 3 + 3 = 36
In der Regel genügt es, das Teilquadrat 1 zu berechnen und dann alle Zellenzahlen der folgenden Teilquadrate um 1 zu erhöhen, was aus obigen 3 Teilquadraten eindeutig zu erkennen ist.
Dazu ein praktisches Beispiel.
Ein 12er Wechselquadrat
Um ein 12er Wechselquadrat zu bilden, sind bei Nutzung des Topquadrates als primäres Ausgangsquadrat 9 Teilquadrate zu bilden und dann nach der Ordnung des Miniquadrates als Sekundärquadrat zusammenzufügen. Die Notwendigkeit der Bindung an das Miniquadrat resultiert aus den nicht einheitlichen magischen Summen, so wie es auch bei der Reihenmethode der Fall ist.
Das so entstandene Quadrat ist magisch, pendelbar und distributiv. Die magische Summe ist 870. Die Zahlenverteilung zeigt keine großen Auffälligkeiten wie beim Reihenquadrat, zumal Mag hier auch eine weitere Unterteilung entsprechend der Teilquadrate weggelassen hat.
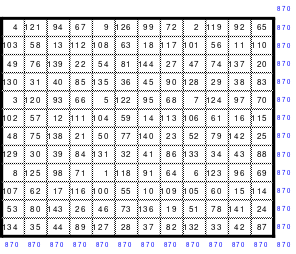
Das 12er Wechselquadrat
Noch günstiger ist die Zahlenverteilung, wenn das kleinere Quadrat als Primärquadrat eingesetzt wird. Nachfolgend ein ebenfalls 12er Wechselquadrat mit dem Miniquadrat als Primärquadrat und dem Topquadrat als Sekundärquadrat. Vom Ausgangsquadrat, dem Miniquadrat, wurden 16 Wechselquadrate gebildet und nach der Struktur des Topquadrates angeordnet. Auch hier sind alle Zahlen von 1 bis 144 im Gesamtquadrat vorhanden. Die magische Summe entspricht auch hier dem Wert von 870. Das Quadrat ist nur pendelbar. Weitere Eigenschaften sind nicht zu finden.
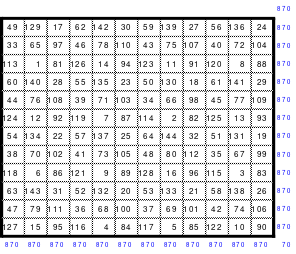
Die Wechselmethode ist natürlich auch für ungerade Quadrate anwendbar. Nachfolgend zeigt Mag ein 15er Kombiquadrat das aus dem 5er Primquadrat als Primärquadrat und dem Miniquadrat als Sekundärquadrat gebildet wurde. Das entstandene Quadrat enthält alle Zahlen von 1 bis 225. Es ist ein magisches mit der richtigen magischen Summe von 1695. Um Sie von der Qualität eines solchen Quadrates zu überzeugen, bittet Sie Mag, das nachfolgende 15er Quadrat zu analysieren um eine Regelmäßigkeit bzw. Gesetzmäßigkeit der Anordnung der einzelnen Zahlen herauszufinden. Sollte Ihnen das gelingen, so kann Ihnen ein hoher Kenntnisstand bei der Gestaltung magischer Quadrate bescheinigt werden.
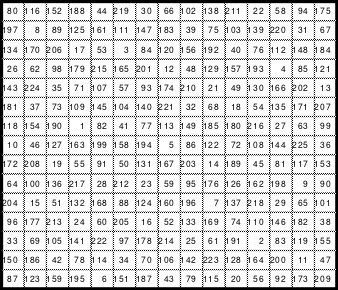
Das 15er Wechselquadrat
Doch nun zu den Einzelheiten dieses Quadrates. Die 9 Teilquadrate der 5. Ordnung, die unter Anwendung der Wechselmethode gebildet wurden sind alle pandiagonal. Die kleinste magische Summe eines Teilquadrates ist 545 und die größte 585. Auch hier zeigt sich, dass die Differenzen zwischen den einzelnen Teilquadraten gering sind. Vor der Einordnung der Teilquadrate nach dem Muster des Miniquadrates hat Mag diese durch Verschiebung von beliebigen Zeilen und/oder Spalten verändert. Weder die kleinsten noch die größten Zahlen der einzelnen Teilquadrate sind an gleicher Stelle zu finden. Diese Möglichkeit ist bei pandiagonalen Quadraten gegeben. Was Mag hier praktiziert hat, ist ein Vorgriff auf den Abschnitt “Chaosquadrate”, in dem die mögliche Veränderung zur Aufhebung von geordneten Strukturen der Quadrate erläutert wird. Des Weiteren hat Mag das Miniquadrat um 90° nach rechts gedreht umso eine zusätzliche Hürde bei der Analyse zu erreichen.
Wenn Sie Näheres erkennen wollen, so unterteilen Sie das 15er Quadrat in 9 Quadrate der 5. Ordnung. Das sind die pandiagonalen Teilquadrate mit den magischen Summen von 545 bis 584. Verschieben Sie noch die Zeilen und Spalten in den einzelnen Teilquadraten so, dass die kleinste Zahl (1, 2, ... oder 9) in die linke obere Ecke kommt, dann haben Sie die einzelnen Teilquadrate entsprechend der Struktur des Pentaquadrates gefunden. Dass die Einordnung in ein um 90° nach rechts gedrehten Miniquadrat erfolgte, hat Mag bereits ausgeführt. Vergleichen Sie nun die Anordnung der 9 kleinen Zahlen und Sie finden die Struktur des gedrehten Miniquadrates. Damit haben Sie schon das Geheimnis des 15er Kombiquadrates gelüftet.
Aus Platzgründen hat Mag Wechselquadrate unter Einsatz des Miniquadrates mit dem Top- und Pentaquadrat dargestellt. Selbstverständlich ist die Verwendung aller magischen Quadrate möglich. So kann ein 42er Wechselquadrat gebildet werden, wenn das Sexta- und das Heptaquadrat nach dieser Methode eingesetzt werden.
Um die Bildung von Wechselquadraten zu vereinfachen hat Mag die Excel-Datei “Wechselquadrate” erstellt, Diese ist im Abschnitt “Helfer PC” zu finden und ermöglicht die Ausgabe gewünschter Wechselquadrate bis zur 18. Ordnung.
4.4. Pendelquadrate
Die Bildung von Pendelquadraten ermöglicht die Gestaltung von ungebundenen größeren magischen Quadraten. Dabei ist der Aufbau der Pendelquadrate ganz einfach und soll am Beispiel eines Topquadrates, ein Quadrat der 4. Ordnung erfolgen. Es soll ein Quadrat der 8. Ordnung entstehen. Dazu muss das Topquadrat 4-mal gependelt werden. Pendeln ist die Art und Weise der fortlaufenden Eintragung der Zahlen, im Beispiel 1 bis 64. In die Zellen 1 werden von links nach rechts die Zahlen 1 bis 4 eingeschrieben. Danach werden die Zahlen 5 bis 8 von rechts nach links in die Zellen 2 eingesetzt. Dann wieder die Zahlen 9 bis 12 von links nach rechts in die Zellen 3 und weiter von rechts nach links, die Zahlen 13 bis 16 in die Zellen 4. So werden alle weiteren Zahlen in die Quadrate eingeschrieben.
Die entstandenen 4 Quadrate haben alle die gleiche magische Summe von 130.
Dieses hin und her des Eintragens entspricht dem Pendeln einer Uhr, woher es auch seine Bezeichnung hat. Die beschriebenen Eintragungen der Zahlen sind in den unten abgebildeten 4 Quadraten gut zu erkennen.
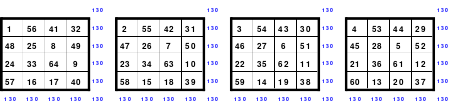
Das so entstandene Quadrat der 8. Ordnung (links) ist nicht nur magisch, sondern auch pandiagonal, was darauf zurückzuführen ist, dass das Topquadrat ein pandiagonales ist.
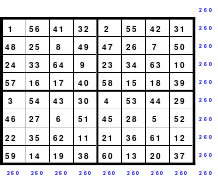
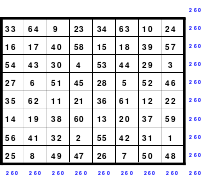
Zum Beweis der Pandiagonalität wurden die 1. Spalte nach hinten und die oberen 2 Zeilen nach unten versetzt (rechte Quadrate). Das Quadrat ist nach wie vor magisch und pandiagonal mit der richtigen magischen Summe von 260. Jede Zahl von 1 bis 64 ist nur einmal vorhanden.
Als weiters Beispiel, ein Pendelquadrat der 18. Ordnung. Es wurde aus dem Hexaquadrat, ein magisches Quadrat der 6. Ordnung, gebildet. Dazu wurde es 9-mal gependelt und zu einem Quadrat der 18. Ordnung zusammengesetzt.
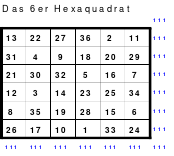
Das gependelte Quadrat der 18. Ordnung mit der richtigen magischen Summe von 2925. Es ist magisch aber nicht pandiagonal, da das 6er Hexaquadrat nicht pandiagonal ist. Alle Zahlen von 1 bis 364 sind lückenlos und nur einmal vorhanden.
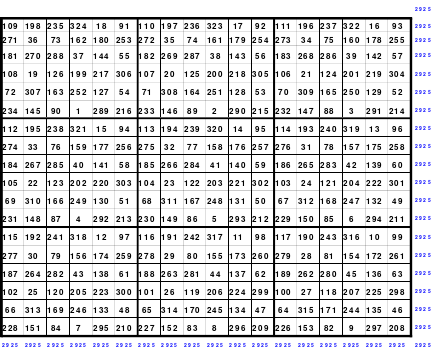
Allgemein kann die Aussage getroffen werden, dass Kombiquadrate dann pandiagonal werden, wenn die eingesetzten Primär- und Sekundärquadrate pandiagonale sind. Dabei ist es egal, ob die Teilquadrate nach der Reihen-, Wechsel- oder Pendelmethode gebildet wurden. Korrekturquadrate scheiden aus, da aufgrund des Tausches von Blöcken diese nicht pandiagonal sein können. Bedingung ist, dass die gebildeten Teilquadrate nicht verändert werden dürfen. Ausnahmen bestätigen auch hier die Regel. So kann ein 8er Kombiquadrat aus 4 gependelten Topquadraten pandiagonal sein, wenn diese in ein Folgequadrat eingeordnet werden. Selbst die Einordnung von gependelten Primquadraten in ein pandiagonales Sekundärquadrat kann zu einem pandiagonalen Kombiquadrat führen.
Da die Bildung der Pendelquadrate nach festen Regeln erfolgt, war auch die Bildung von Formeln zur Berechnung der Pendelquadrate gegeben, was auch den Einsatz des Computers ermöglicht hat.
(Siehe dazu unter “Helfer PC”, “Pendelquadrate”, eine Excel-Datei.)
Diese Formeln sind: Für die geraden Zahlen Zn=Za*Tg+1-Tn und für die ungeraden Zahlen Zn=(Za-1)*Tg+Tn
Es bedeuten: Zn = neue Zellenzahl
Za = Zellenzahl im Ausgangsquadrat
Tg = Gesamtanzahl der Teilquadrate
Zn = Das aktuell zu berechnende Teilquadrat
Durch das gependelte Eintragen der Zahlen erfolgt stets ein Ausgleich der Summen, wodurch die magischen Summen der einzelnen Teilquadrate alle die gleiche Größe haben. So ist in den 4er Pendelquadraten zum Beispiel die Summe der ersten beiden Zahlen in allen 4 Quadraten gleich. Sie beträgt 1+8=9, 2+7=9, 3+6=9 und 4+5=9. Diese Form der Eintragung ist der Bildung von Duoreihen ähnlich.
Es ist verständlich, dass ungerade Quadrate, wie das 5er oder 7er, nicht pendelfähig sind, denn hier würde der Ausgleich nicht erfolgen und die Teilquadrate hätten keine einheitlichen Reihensummen und wären damit auch nicht magisch.
Mag hat jedoch eine Möglichkeit geschaffen, mit der auch ungerade, vorwiegend pandiagonale Primquadrate, durch Austausch von Blöcken in gleich große Quadrate umgewandelt werden können. Die Beschreibungen dazu erfolgen in der nächsten Datei “Korrekturquadrate” und auch unter “Helfer PC”, “Korrekturquadrate”.
4.5. Die Korrekturmethode
Bei den einzelnen Methoden war es nicht möglich ungerade Quadrate zu bilden, die aus mehreren, gleich großen, ungeraden Quadraten bestehen. Das war nur durch die Pendelmethode mit geraden, pendelbaren Quadraten zu erreichen. Um diesen Mangel abzuhelfen, hat Mag die Korrekturmethode entwickelt. Ziel ist es, durch Austausch von Blöcken ungerade Teilquadrate mit einheitlichen magischen Summen zu bilden.
Die Korrekturmethode ist keine eigenständige Methode, sondern eine Ergänzung insbesondere der Wechselmethode.
Korrektur von Primquadraten
Mag wird nun die Korrekturmethode anhand von 9 magischen Wechselquadraten der 5. Ordnung, die auf der Grundlage des 5er Primquadrates (Pentaquadrat) erstellt wurden, erläutern.
Als erstes die 9 Wechselquadrate der 5. Ordnung.
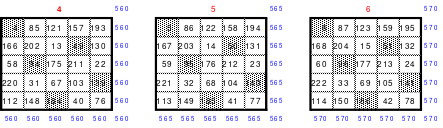
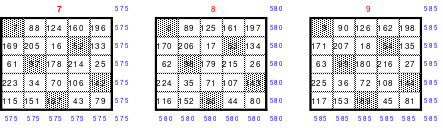
Mag ging davon aus, dass es möglich sein muss, diese Differenzen bei den magischen Summen durch den Austausch der einzelnen Blöcke so zu verändern, dass die magischen Summen in allen Teilquadrate gleich groß werden.
Das ist gelungen was er am Beispiel aufzeigen wird.
Damit Sie die einzelnen Schritte besser nachvollziehen können, hat Mag bei den Wechselquadraten die ersten Zellenzahlen der einzelnen Blöcke grün markiert. Er weist auch darauf hin, dass die Abstände von Block zu Block ebenfalls gleich sind. Sie sind das Produkt von Ordnungszahl multipliziert mit der Anzahl der zu bildenden Quadrate. Im Beispiel ist das 5 x 9 = 45. Wenn Mag den Tausch der Blöcke nennt, so nennt er zum besseren Verständnis nur die erste Zahl des Blockes, die er Leitzahl nennt, und nicht alle Zahlen des Blockes.
Nun zu den einzelnen Schritten die als Beispiel zu verstehen sind. Es sind auch andere Varianten denkbar. Um eine gute Übersicht zu haben hat sich Mag nur auf das Wesentliche konzentriert, welches in der folgenden Tabelle aufgeführt ist.
In der 1. Tabelle (Abb. 1) sind die Nummern der Quadrate, deren magische Summen und die Differenzen zum mittleren Quadrat, dem 5., mit einer magischen Summe von 565 ausgewiesen.
Bei den folgenden Tauschvorgängen ist zu beachten, dass die mittlere, die 5. Spalte möglichst nicht in den Tausch einbezogen wird. Besonders bei vielen Teilquadraten muss die Mitte als Reserve verbleiben. Lediglich in den Fällen, wo die Anzahl der Teilquadrate gleich oder kleiner der Ordnungszahl der Teilquadrate ist, bietet sich der Tausch auch mit der Mitte an. Mag wird das anhand eines Quadrates der 15. Ordnung, das sich aus 9 Quadraten der 5. Ordnung zusammensetzt beschreiben. Des Weiteren werden immer primär die Spalten bearbeitet, die zur Mitte den gleichen Abstand haben, wobei von außen nach innen vorgegangen wird. Eine feste Regel kann nicht vorgegeben werden. Es kann durchaus möglich sein, dass ein angestrebter Weg nicht zu einer Lösung führt. Dann muss eben ein anderer Weg beschritten werden.
Im Beispiel wird mit den Spalten 1 und 9 begonnen. Die Spate 1 muss um 20 erhöht und die Spalte 9 um 20 reduziert werden. Der Tausch des Blockes 1 vom Quadrat 1 mit Block 9 vom Quadrat 9 bringt einen Ausgleich von 8. Auch der Tausch des Blockes 46 mit den Block 54 dieser beiden Quadrate bringt ebenfalls einen Ausgleich von 8 (Siehe blaue Markierung). Es fehlen noch 4 zum vollständigen Ausgleich. der wird erreicht durch Tauschen der Blöcke 91 mit 92 und 136 mit 139 (gelb), sowie 99 mit 98 und 144 mit 141(rot). Damit wird der Ausgleich der Quadrate 1 und 9 geschafft, gleichzeitig aber die Quadrate, bzw. Spalten 2, 4, 6 und 8 verändert.
Diese Veränderungen sind in der Abb. 2 eingearbeitet. Sowohl die ersten Zahlen der Blöcke, als auch die neuen magischen Summen und deren Differenz zu 565 sind dargestellt. Gleichzeitig sind die Spalten 1 und 9, was zugleich die Quadrate 1 und 9 bedeutet, grün markiert, als Zeichen dafür, dass diese Quadrate fertig gestellt sind.
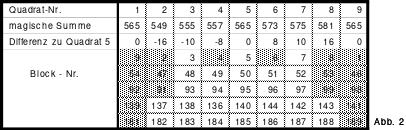
Jetzt kann die Bereinigung der nächsten Quadrate vorgenommen werden. Dabei dürfen natürlich keine Blöcke aus den fertig gestellten Quadraten einbezogen werden. Das Tauschen ist wieder farbig gekennzeichnet.
STOP!!!
Diese Methode, die eine reine Puzzlearbeit ist, wird sicherlich nicht begeistert aufgenommen und eher der Wechselmethode der Vorzug gegeben.
Sie zeigt aber wie Mag begonnen hat, eine Lösung zu finden.
Gleichzeitig wird ein möglicher Weg zu einem Ergebnis gezeigt, der ausbaufähig ist.
Mag hat diese Methode weiterentwickelt, indem er nur 3 Blöcke nach der Wechselmethode belassen hat und die übrigen Blöcke in den Quadraten, die ja eine gerade Anzahl sind, durch Pendeln gleichgroß gemacht. Dadurch konnten die Differenzen zwischen den Quadraten vermindert werden und die jeweils 3 nicht gependelten, Blöcke, reichten aus um einen erfolgreichen Tausch vorzunehmen.
Die so gefundenen Lösungen wurden immer mehr verbessert. Dabei ist es Mag gelungen empirische Formeln zu bilden, die den Tausch mittels Computer ermöglichen.
Die so entstandene Datei ist unter den Namen “Korrekturquadrate” als Excel-Datei im Teil “Helfer PC” zu finden.
Es brauchen nur 3 Eingaben, die Ordnungszahl, die Anzahl der insgesamt gewünschten Quadrate und das jeweils aktuelle Quadrat gemacht werden und das Programm gibt das korrigierte Quadrat aus. Es können korrigierte Primquadrate bis zur 19. Ordnung, auch das 3er abgerufen werden. Diese sind magisch, mit gleichen magischen Summen und können wahllos zu größeren Quadraten zusammengesetzt werden, die ebenfalls magisch sind und alle Zahlen von 1 bis n lückenlos und nur einmal enthalten. Lediglich beim 3er muss beachtet werden, dass nur ein Quadrat magisch und die anderen nur teilmagisch sind, was bei der Zusammensetzung zu beachten ist.
Unter “Helfer PC” finden Sie auch die weiteren Erläuterungen zu den Korrekturquadraten und deren mathematischen Lösung. (Besonders für Fans gedacht.)
Mittels der Erfahrungen, die bei der Entwicklung des PC-Programms gemacht wurden, ist auch eine rationelle Erstellung von Korrekturquadraten ohne Einsatz eines Computers möglich und wird nachfolgend beschrieben.
Bildung von Korrekturquadraten ohne Einsatz eines Computers
Mag erkannte, dass für die Bildung der Korrekturquadrate nur 3 Blöcke notwendig sind. Das bedeutet allerdings auch, dass die übrigen Blöcke durch entsprechende Veränderungen gleich groß sein müssen, was durch das Pendeln ermöglich wird.
Auf dieser Erkenntnis aufbauend suchte er nach entsprechenden Lösungen. Im Ergebnis fand er den Algorithmus, der die Bildung von Formeln ermöglicht. Das Ergebnis wird in den nachstehenden Tabellen vorgestellt.
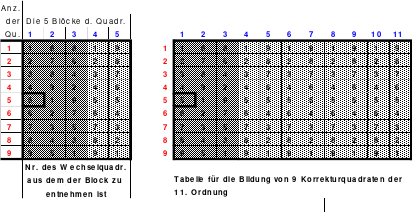
Links ist die Tabelle für das Pentaquadrat, ein Quadrat der 5. Ordnung, in der aufgezeigt wird, wie eine Einordnung der Blöcke möglich ist, um alle Quadrate gleichgroß zu gestalten.
Es sollen insgesamt 9 Korrekturquadrate der 5. Ordnung entstehen. Die roten Zahlen sind die Nummern der 9 zu bildenden Korrekturquadrate. Die blauen stehen für die jeweils 5 Blöcke. Alle schwarzen Zahlen besagen, aus welchem Wechselquadrat der entsprechende Block einzusetzen ist.
Zum Beispiel sind in das 3. Korrekturquadrat (rote 3) einzusetzen:
als 4. Block der 4. Block aus Wechselquadrat 3, (d. h. keine Änderung)
als 5. Block der 5. Block aus Wechselquadrat 7,
als 1. Block der 1. Block aus Wechselquadrat 3, (d. h. keine Änderung)
als 2. Block der 2, Block aus Wechselquadrat 8 und
als 3. Block der 3. Block aus Wechselquadrat 4.
(Die 9 Wechselquadrate der 5. Ordnung wurden am Anfang der Erläuterung
abgebildet.)
Die erfolgten Änderungen sind in der Abbildung rechts zu erkennen.
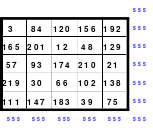
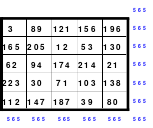
Das rechte Quadrat ist magisch mit der jetzt richtigen magischen Summe von 565. Das linke Quadrat ist zum Vergleich das Ausgangsquadrat, das 3. Wechselquadrat.
So können alle 9 Wechselquadrate in 9 Korrekturquadrate mit der einheitlichen magischen Summe von jeweils 565 umgewandelt werden und zu einem Quadrat der 15. Ordnung mit der magischen Summe von 1695 zusammengefügt werden.
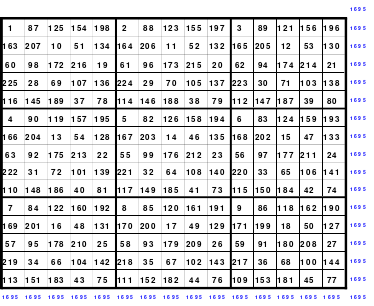
Die einzelnen Quadrate wurden absichtlich ohne jegliche Veränderung eingesetzt.
In dieser Form können weitere ungerade Kombiquadrate erstellt werden. So z. B. ein Quadrat der 9. Ordnung durch 3 mal 3 Korrekturquadrate der 3. Ordnung oder auch sehr große Quadrate, wie ein Quadrat der 85. Ordnung, das aus 25 Korrekturquadraten der 17. Ordnung besteht.
(Dazu sollte allerdings die Excel-Datei “Korrekturquadrate” genutzt werden.)
Die Gestaltung der Tabellen ist leicht zu erkennen.
Im grünen Bereich wird die gleich große Summe für die Blöcke 4 bis n durch eine gegenläufige Eintragung der Anzahl der zu bildender Quadrate erreicht. Die gegenläufige Eintragung erfolgt in die Blöcke mit ungerader Zahl.
Bei den Blöcken 1 bis 3 (blauer Bereich) konnte nicht so einfach verfahren werden. Der Grund ist, dass die Summen aus diesen 3 Böcken das 1,5-fache der Summe von jeweils 2 Blöcken aus dem grünen Bereich ergeben müssen. Im Beispiel ist das 1,5 * (1 + 9) = 15.
Dazu wurde folgende Lösung gefunden:
In die Spalte 1 (für Block 1 im jeweiligen Quadrat) werden die Blöcke von oben nach unten eingetragen.
In die Spalte 2 erfolgt die Eintragung in gleicher Weise, allerdings ab der mittleren Zeile, die hier für das 5. Korrekturquadrat steht. Unten angekommen, wird von oben aus weiter eingetragen.
In die 3. Spalte wird dann nur noch die Ergänzung der Summe aus Spalte 1 und 2 zur Summe 15 eingesetzt. Das Ergebnis ist als Regel erkenntlich. Die Eintragung erfolgt von unten nach oben. Dabei wird mit den ungeraden Zahlen begonnen und nach der Mitte mit den geraden Zahlen beendet.
Die Abbildung weiter vorn rechts ist die Tabelle für ein Quadrat der 11. Ordnung, für das ebenfalls 9 Korrekturquadrate erstellt werden sollen.
Die weitere Analyse ergab, dass auch bei der Bildung einer anderen Anzahl von Korrekturquadraten diese Ordnung zutrifft, was am folgenden Beispiel gezeigt wird.
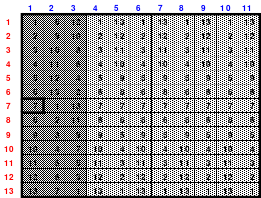
Tabelle für die Bildung von 13 Korrekturquadraten
der 11. Ordnung. Hier muss die Summe der Blöcke
1 bis 3 = (1 + 13) * 1,5 = 21 sein.
Wichtig ist der Hinweis, dass diese Methode nur bei den perfekten, pandiagonalen Quadraten zu einer völlig zufriedenen Lösung führt. Andere ungeraden Quadrate, wie z. B. 9er, können nur erschwert zu einheitlichen magischen Quadraten korrigiert werden. Des Weiteren ist diese Methode nur anwendbar, wenn die Anzahl der zu korrigierenden Quadrate ungerade ist, das bedeutet, dass z. B. nicht 4 perfekte 5er oder 7er Quadrate zu einheitlichen Quadraten korrigiert werden können. In einem solchen Fall würden die magischen Summen der Teilquadrate keine ganzzahligen Werte ergeben.
Eine Sonderstellung nimmt dabei das 3er Miniquadrat ein. Es ist kein pandiagonales Quadrat und folglich nur bedingt als Korrekturquadrat einsetzbar. Dazu ein Beispiel:
Quadrat der 3. Ordnung. Alle anderen Zahlenreihen erfüllen diese
Bedingung nicht.
Trotzdem kann ein magisches Quadrat der 9. Ordnung gebildet werden. Dazu müssen die 3er Teilquadrate so zusammengefügt werden, dass das 9. Quadrat in die Mitte kommt. Ansonsten genügt das Wenden von 2 Teilquadraten um die senkrechte Achse um die richtige Diagonale zu einer fallenden zu machen. In der Abbildung sind ausnahmsweise die Diagonalen blau gekennzeichnet.
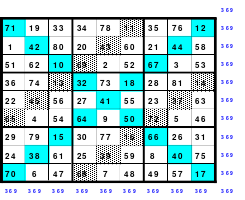
Im weiteren Beispiel wird ein magisches Quadrat der 21. Ordnung gebildet.
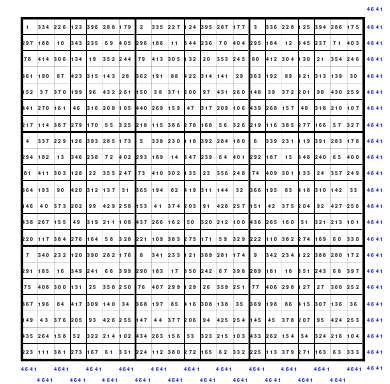
Dazu wurden 9 Korrekturquadrate der 7. Ordnung beliebig zusammengesetzt. Die magische Summe ist mit 4641 richtig. Auch sind alle Zahlen von 1 bis 441 nur einmal vorhanden.
Eine Nachbetrachtung
Die Bildung von Korrekturquadraten können einfacher durch direkte Berechnung der Zahlen für die Korrekturquadrate erstellt werden. Damit kann der etwas umständliche Weg über Wechselquadrate und Übertragung von ganzen Blöcken aus anderen Wechselquadrate in die Korrekturquadrate umgangen werden.
Die Formel dafür ist: Zn=(Bn-1)*A*O+Qn
Darin bedeuten: Zn = 1.Zahl im Block Bn
Bn = Block für den die 1. Zahl berechnet werden soll
A = Anzahl der zu bildenden Korrekturquadrate
O = Ordnungszahl der Korrekturquadrate bzw. Ausgangsquadrate
Qn = Quadrat aus dem der Block zu entnehmen ist (Wird der Matrix entnommen.)
Als Beispiel soll die 1. Zahl für Block 3 im 5. Korrekturquadrat berechnet werden. Es sollen 9 Korrekturquadrate der 7.Ordnung entstehen. Die 9 Korrekturquadrate der 7. Ordnung können dann zu einem Quadrat der 21. Ordnung zusammengefügt werden.
Beachte dazu die Matrix (links) und das Quadrat.
Das ist: (3-1) *9*7+9=135 (siehe blau schattierte Zahl im Quadrat)
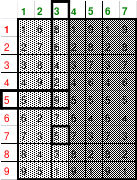
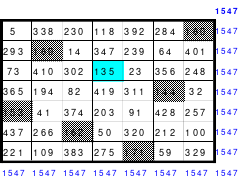
Die restlichen Zahlen des 3.Blockes werden durch jeweilige Erhöhung der Zahlen um die Anzahl der zu bildenden Korrekturquadrate berechnet und nach einem Rechtssprung in die Zellen eingesetzt. Siehe dazu die grün schattierten Zellen mit den Zahlen 144, 153, 162 bis 189, die schrittweise um 9 erhöht sind.
Die 1. Zahl des 3. Blockes im Quadrat 7 ist nach dieser Formel: (3-1) *9*7+5=131. Das ist 4 weniger als 135 für das 5. Quadrat, was auch die Differenz zwischen den Matrixzahlen 9 und 5 ist. Das ist logisch, denn für beide Quadrate gilt der gleiche Teil der Formel (3-1) *9*7=2*63=126. Er wirkt wie eine Konstante wobei lediglich die unterschiedlichen Zahlen aus der Matrix zugerechnet werden. Das wäre für Quadrat 1: 126+8=134, für Quadrat 2: 126+6=132 usw. bis zum Quadrat 9: 126+1=127. Die so ganz einfach berechneten 1. Zahlen der 3. Blöcke in den Quadraten 1 bis 9 sind in der rechten Tabelle dargestellt.
Aber es geht noch einfacher! Man berechnet die 1. Zahl im Block. Die Zahlen für die 1. Zahl im nächsten Quadrat werden berechnet mit +/- der Differenz zur nächsten Matrixzahl. Das ist in der rechten Tabelle zu erkennen. Bei den Blöcken 1, 4 und 6 ist diese Differenz nur +1 und bei den Blöcken 5 und 7 ist die Differenz -1.
Diese mathematischen Regeln hat Mag zu einem späteren Zeitpunkt durch Analysen erkannt, weshalb sie in der Nachbetrachtung beschrieben werden.
Und auch diese sind nicht das Letzte zu den Korrekturquadraten. Da die mathematischen Regeln erarbeitet sind, ist auch eine Berechnung mittels PC gegeben. Wie bereits am Anfang dieser beschrieben, hat Mag ein Excel-Programm erstellt mit dem die Korrekturquadrate berechnet und ausgegeben werden können. Das Excel-Programm “Korrekturquadrate” finden Sie im Abschnitt “Helfer PC”.
5 Chaosquadrate
Chaosquadrate sind keine eigenständigen Quadrate, sondern Quadrate die u. a. wie bisher beschrieben gebildet, aber anschließend so umgestaltet werden, dass deren Ordnung aufgehoben, bzw. nur schwer erkennbar ist. Dabei gilt, dass die Umwandlung nur so erfolgen darf, dass das Quadrat als magisches erhalten bleibt.
Die bisher gebildeten magischen Quadrate hat Mag weitgehend unverändert dargestellt. Dadurch haben Sie die Möglichkeit, die einzelnen Schritte bei deren Bildung zu verfolgen, wodurch Sie sich das erforderliche Wissen besser aneignen können. Mag hat gezeigt, dass nahezu alle Quadrate durch Analyse und Synthese aus dem Miniquadrat und dem Dürerquadrat entstanden sind. So wie Mag sind auch Andere in der Lage durch analytische Arbeit die einzelnen Methoden zu entschlüsseln.
Um die Analysen zu erschweren hat Mag Prinzipien zur Bildung von Chaosquadraten erarbeitet. Diese ermöglichen es, die magischen Quadrate durch ein geordnetes Chaos so zu verändern, dass deren Struktur nicht ohne weiteres erkennbar ist. Des Weiteren hat die Bildung von Chaosquadraten auch die Zielstellung, wenig attraktive Quadrate optisch aufzuwerten. Das trifft unter anderem auf die Quadrate zu, die mittels der Diagonal- oder Reihenmethode gebildet wurden.
Ehe Mag auf einige dieser Prinzipien eingeht, möchte er darauf hinweisen, dass durch geschickte Anwendung des bisher gelernten bereits die Quadrate in kleiner Form umgestaltet werden können. Durch Versetzen von Reihen, Wenden um die Achsen kann bereits die Struktur so verändert werden, dass es eine Analyse erschwert. Auch bei den ungeraden Quadraten sind Möglichkeiten gegeben. Durch Nutzung von Doppel- oder Dreifachsprung, oder dem freien Springen bei größeren Quadraten kann die Systematik des Aufbaues unkenntlicher gemacht werden. Werden perfekte Quadrate zu einem größeren zusammengefügt, so sollten die Teilquadrate nach der Wechselmethode gebildet werden, weil diese die Versetzung von Reihen ermöglicht, denn diese sind pandiagonal. In dieser Form finden Sie sicherlich weitere Möglichkeiten. Hier ein Beispiel mit pandiagonalen Quadraten.
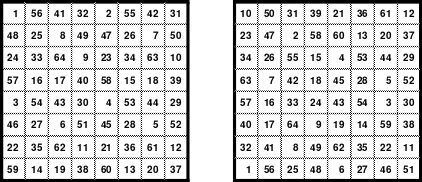
Das linke pandiagonale Quadrat der 8. Ordnung mit der magischen Summe von 230 setzt sich aus 4 gependelten Topquadraten zusammen. Die Struktur ist zu erkennen. Für das rechte Quadrat wurden die Quadrate beliebig eingefügt. Vorher wurden jedoch noch Reihen und/oder Zeilen versetzt. Ein Quadrat wurde belassen, bei einem 2 Zeilen, bei einem 2 Spalten und beim letzten 2 Reihen und 2 Spalten versetzt. Das Quadrat ist magisch, aber nicht mehr pandiagonal, was in der Regel bei Chaosquadraten zutrifft.
Da die Chaosquadrate einige Eigenschaften, wie pandiagonal, homogen usw. verlieren können, sollte die Umgestaltung zu Chaosquadraten erst am Schluss der Bildung von magischen Quadraten erfolgen.
Eine weitere Möglichkeit der Reihenverschiebung besteht, wenn das ganze Kombiquadrat ebenfalls pandiagonal ist, wie z. B. das links oben gezeigte Quadrat der 8. Ordnung.
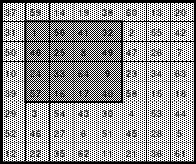
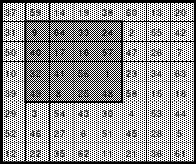
Durch verschieben der unteren Zeile nach oben und der hintere Spalte nach vorn entstand das linke Quadrat. Es ist magisch und pandiagonal. Durch eine farbige Gestaltung ergibt sich ein ziemlich attraktives Quadrat und Sie können stolz verkünden: “Dieses Quadrat der 8. Ordnung ist ein magisches mit der magischen Summe von 260. In diesem Quadrat ist ein exzentrisch eingefügtes Quadrat der 4. Ordnung mit der magischen Summe von 130 enthalten.”
Damit sind jedoch noch nicht alle Möglichkeiten der Umgestaltung ausgeschöpft. Das 4er Quadrat ist ein pandiagonales und kann somit noch verändert werden. Das ist aber nicht ganz leicht. Die fallende Diagonale des 4er Quadrates befindet sich voll und ganz in der fallenden Gesamtdiagonale. Das trifft allerdings nicht auf die steigende Diagonale zu. In dieser ist das 4er lediglich mit den Zahlen 17 und 9 in der Gesamtdiagonalen enthalten. Bei einer Veränderung des 4er muss gesichert werden, dass die Summe von 17+9=26 erhalten bleibt. Dies ist nur möglich durch den Tausch der Zahlen 1+25 (oben links) mit den Zahlen 17+9. Das kann aber nicht durch einen einfachen Tausch erfolgen. Das gewünschte Ergebnis wird durch das Wenden des 4er Quadrates um seine senkrechte Achse und anschließende durch Versetzen der oberen beiden Zeilen nach unten erreicht. Der Tausch ist perfekt und ist das Ergebnis des rechten 8er Quadrates. Es ist magisch mit der magischen Summ von 260. Ebenfalls das 4er mit 130 als magische Summe. Die letzte Änderung führt dazu, dass das Quadrat nicht mehr pandiagonal ist.
Mag wird die vorangegangenen kleinen Möglichkeiten bei den weiteren Erläuterungen zu den Prinzipien der Umgestaltung von magischen Quadraten in Chaosquadrate nicht nutzen, damit Sie den Darlegungen besser folgen können. Es bleibt Ihnen überlassen, diese vor einer Umgestaltung zusätzlich zu nutzen.
5.1 Das Rautenprinzip
Das Rautenprinzip ist im Gegensatz zum Splittingprinzip für alle magischen Quadrate geeignet. Beim Rautenprinzip werden Zeilen und Spalten ausgetauscht. Wichtig ist dabei, dass die Zeilen gleiche Abstände zur Achse haben müssen, ebenso die Spalten.
Nur so wird erreicht, dass die Zahlen der Diagonalen wieder in die Diagonalen eingeordnet werden. Das erfolgt in diesem Fall nicht in die andere, sondern in die gleiche Diagonale.
Beim Rautensystem sind zwei unterschiedliche Varianten möglich. Bei der ersten werden die Zeilen und Spalten innerhalb einer Raute getauscht, auch wenn mehrere Rauten vorgesehen sind. Bei der zweiten Variante werden die Zeilen und Spalten zwischen mehreren Rauten ausgetauscht. Ehe Mag zu den beiden Varianten im Einzelnen kommt, soll das Rautenprinzip an einem Beispiel eines Pentaquadrates demonstriert werden. Abb. 1 zeigt das unveränderte Pentaquadrat. Die Zeilen und Spalten die getauscht werden sollen sind blau gekennzeichnet. Sie bilden eine Raute. Alle Zeilen und Spalten haben zur Mitte eine gleiche Entfernung.
Als erstes werden die Spalten 2 und 4 getauscht. Das Zwischenergebnis ist in Abb. 2 zu erkennen. Die Summen der Spalten und Zeilen sind geblieben, nicht aber die der Diagonalen. Nun werden im 2. Quadrat die Zeilen b und d getauscht. Abb. 3 zeigt das fertige Chaosquadrat. Es ist ein magisches, aber kein pandiagonales mehr. Deutlich ist zu erkennen, dass sich die Zahlen 23 und 12 der fallenden Diagonale weiterhin in der fallenden Diagonale befinden, jedoch haben sie die Plätze getauscht. Das Gleiche trifft auf die Zahlen der steigenden Diagonale zu.
Die Abb. 3 zeigt auch, dass die einfache Springermethode, nach dem das Pentaquadrat gebildet wurde, nicht mehr zu finden ist. Aus der Zuordnung der einzelnen Zahlen zueinander ist kein System erkennbar.
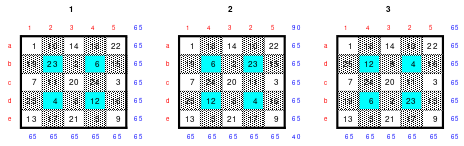
Wichtig ist, dass für den 2.Tausch, in diesem Falle der Tausch der Zeilen, der Tausch nicht nach dem unveränderten Quadrat nach Abb. 1 erfolgt, sondern auf der Basis des durch den 1. Tausch veränderten 2. Quadrat. Wird das nicht beachtet, kommt es zu falschen Summen der Diagonalen.
Nachfolgend ein aus 4 gependelten Topquadraten bestehendes 8er Quadrat. Abb. 1 zeigt das unveränderte Quadrat in das 2 Rauten, blau und grün, eingeordnet wurden. Es erfolgt der Tausch innerhalb jeder Raute. Folglich wird die Spalte 1 mit Spalte 8 und Spalte 3 mit Spalte 6 getauscht. Abb. 2 zeigt das Zwischenergebnis. Nun werden auf der Grundlage des 2. Quadrates die Zeilen a und h, sowie c und f getauscht. Abb. 3 zeigt das fertige Chaosquadrat, aus dem Sie weitere Einzelheiten entnehmen können. Zur weiteren Betrachtung hat Mag das Quadrat 3 als 4. Quadrat ohne Schattierung, Zeilen- und Spaltenkennzeichnung abgebildet. Auch hier sind die Strukturen des Quadrataufbaues nicht mehr zu erkennen. Allerdings treten Eigentümlichkeiten in Form von jeweils 4 zusammenhängenden Zahlen auf. Mag hat diese rot hinterlegt. Das ist Zufall und ohne Bedeutung. Eine Ordnung kann daraus nicht abgeleitet werden, denn diese Zufälle treffen auf die übrigen Bereiche des Quadrates nicht zu.
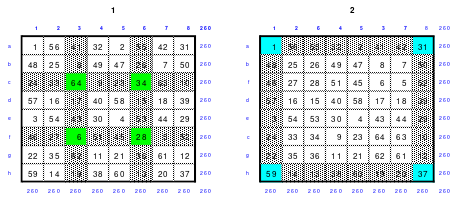
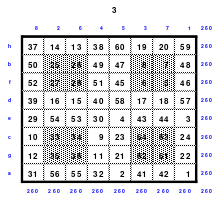
Derartige Zufälle können durch die 2. Variante ausgeschlossen werden. Sie ergeben auch ein besseres Quadrat, insbesondere bei Einsatz von Quadraten die nach der Wechselmethode gebildet wurden. Zur Demonstration hat Mag ebenfalls das vorige 8er Quadrat und die gleichen Rauten gewählt.
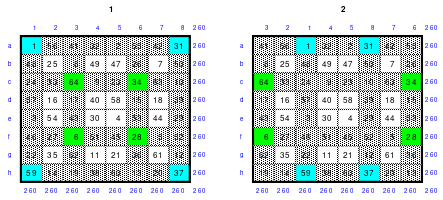
Bei dieser Variante werden die Zeilen und Spalten zwischen den Rauten ausgetauscht. Abb. 2 zeigt den erfolgten Austausch der Spalten 1 (blau) und 3 (grün), sowie 6 (grün) und 8 (blau). Analog werden die Zeilen getauscht. Abb. 3 und 4 zeigen das Endergebnis, ein besseres als beim Tausch innerhalb der Rauten.
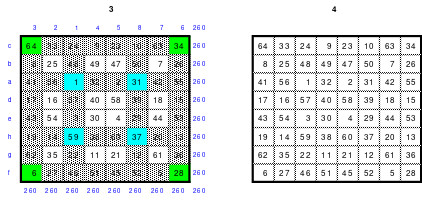
Dass mit der Variante 2 wesentlich bessere Ergebnisse erreicht werden können, zeigt Mag noch am Beispiel eines nach der Additionsmethode erstelltes Quadrat der 9. Ordnung. Links das Ausgangsquadrat und rechts das Chaosquadrat. Es wurden die Spalten 2 mit 4 und 6 mit 8, sowie die Zeilen b mit d und f mit h getauscht. Die Strukturen wurden auch hier vollständig aufgehoben.
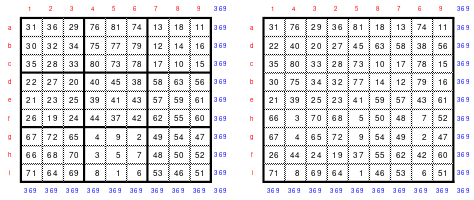
Beim Rautenprinzip gilt, dass nur etwa die Hälfte der Zeilen und Spalten getauscht werden dürfen. Diese Regel schließt bei kleineren Quadraten die Anwendung der Variante 2 aus.
Das Splittingprinzip
Das Splittingprinzip kommt bei Kombiquadraten, wie den Additions-, Wechsel- und Pendelquadraten zur Anwendung. Bei diesem Prinzip werden die einzelnen Teilquadrate in gleich große Abschnitte aufgesplittet und versetzt zusammengefügt. Dabei werden die einzelnen Abschnitte so positioniert, dass sie sich in den Zeilen, Spalten und Diagonalen im großen Quadrat wieder zur magischen Summe ergänzen, ohne dass sie wieder komplette Teilquadrate bilden. Das Gesagte wird am Beispiel eines 12er Quadrates, das sich aus 4 gependelten 6er Quadraten zusammensetzt, verständlich gemacht. Die Teilquadrate sind farblich unterschiedlich gestaltet und in der folgenden Abbildung dargestellt.
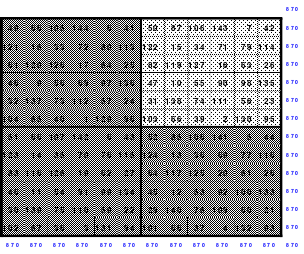
Die 4 Teilquadrate wurden in 4 Abschnitte in der Größe 3 x 3 Zellen unterteilt. Danach wurden die 1. Abschnitte der 4 Teilquadrate zu einem 6 x 6 großen Teil verbunden. Das Gleiche erfolgte mit den anderen Teilen. Aus der nächsten Abbildung ist die Verteilung zu erkennen. Es existiert in diesem 12er Quadrat kein 6er mehr. Die Strukturen sind aufgehoben. Trotzdem ist es ein magisches Quadrat geblieben. Die magische Summe mit 870 ist in allen Reihen richtig.
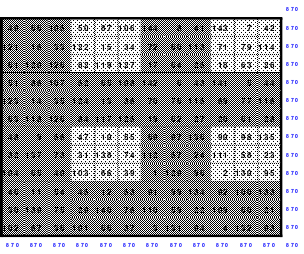
Das gleiche 12er Quadrat kann natürlich auch in Quattros mit je 4 Zellen aufgeteilt und wie im vorangegangenen Beispiel zusammengesetzt werden. Das so entstandene 12er Quadrat ist magisch mit der magischen Summe von 870. Es ist pendelbar, denn in jeder Reihe befinden sich 6 gerade und 6 ungerade Zahlen und es ist distributiv, denn in jeder Reihe befinden sich jeweils 6 Zahlen kleiner 73 und 6 Zahlen größer 72. Diese Eigenschaften treffen auch auf das zuerst aufgeführte Beispiel zu. Weiter Eigenschaften sind nicht vorhanden.
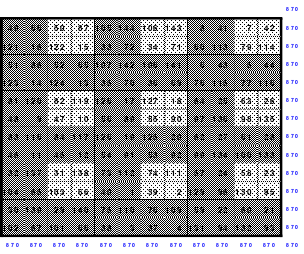
Eine andere, weitaus günstigere, aber auch etwas komplizierte Variante ist das Aufsplitten gependelter vollkommener Quadrate in Quattros und deren unregelmäßige Zusammensetzung zum neuen Quadrat. Dazu ein Beispiel mit 9 gependelten Topquadraten, die nach dem Miniquadrat zu einem 12er Quadrat zusammengefasst wurden.
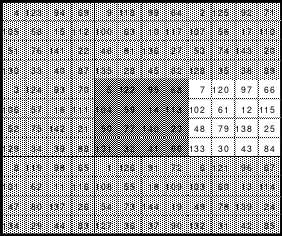
Bevor es jedoch an die Zusammensetzung der 36 Quattros geht, sind eine Analyse der einzelnen Quadrate und deren Quattros erforderlich. Zergliedert man nämlich die gependelten Quadrate in Quattros, vorausgesetzt sie wurden aus einem einheitlichen vollkommenen Quadrat gebildet, so haben diese gleiche Erscheinungsbilder, jedoch wechseln diese in insgesamt 4 Varianten. Im nachfolgenden Bild wurden das gelbe und das zyanfarbene Quadrat in Quattros geteilt und deren Reihensummen gebildet.
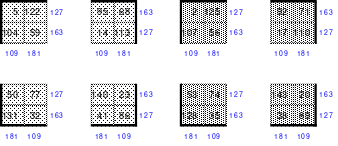
Alle Quattros haben 109 und 181 als Spaltensumme. Die Zeilensummen sind einheitlich 127 und 163. Nur die Diagonalen haben keine gleiche Größe. Je nach Wahl des zu pendelten vollkommenen Quadrates können auch die Diagonalen 2 gleiche Größen haben. Allerdings werden dann die Summen der Zeilen oder Spalten ungleich.
Die Zusammensetzung der 36 Quattros zu einem Chaosquadrat erfolgt unregelmäßig, wobei die Unregelmäßigkeit allerdings begrenzt ist, denn bestimmte Grundsätze müssen schon beachtet werden.
Als erstes müssen jeweils 2 Quattros aus 3 Teilquadraten so in die Diagonalen eingesetzt werden, dass die Diagonalen die erforderliche magische Summe von 870 ergeben. Durch die farblich gekennzeichneten Quattros kann die Einordnung erkannt werden.
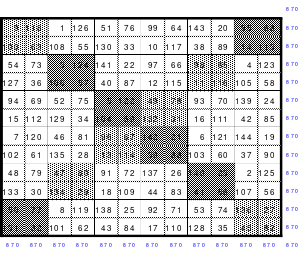
Die restlichen Quattros werden nun in die verbleibenden Lücken so eingesetzt, dass auch bei den Zeilen und Spalten die magische Summe von 870 erreicht wird. Dabei können eventuell 4er Teilquadrate entstehen, deren Zeilen- und Spaltensummen gleiche Summen haben, jedoch falsche Summen bei den Diagonalen.
Eine komplexe Anwendung
Nachfolgend wird Mag ein Beispiel zeigen, bei dem die Strukturen einzelner Quadrate verschieden verändert werden, um aus den einheitlichen Strukturen der Teilquadrate uneinheitliche zu gestalten, um so eine Analyse zu erschweren, bzw. unmöglich zu machen. Dabei soll aber die Besonderheit dieses Quadrates nicht aufgehoben werden. Das folgende 15er Quadrat ist ein magisches mit der magischen Summe von 1695. Es besteht aus 9 Teilquadraten der 5. Ordnung. Das Besondere dieses Quadrates besteht darin, dass alle Teilquadrate gleich große Quadrate mit einer magischen Summe von 565 sind. Das konnte nur durch die Anwendung der Korrekturmethode erreicht werden. Die Anordnung der Teilquadrate und deren gleichmäßige Struktur ist leicht zu erkennen. Es sind Quadrate, die denen der Wechselmethode entsprechen. Lediglich in den einzelnen Blöcken treten Differenzen auf. Sie sind nicht kontinuierlich untereinander. Gerade diese sind es, die das Geheimnis der Korrekturquadrate durch eine einfache Analyse offenbaren.
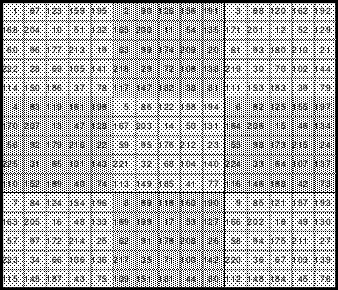
Um das zu verhindern, hat Mag die einzelnen Teilquadrate nach unterschiedlichen Prinzipien zur Bildung von Chaosquadraten so umgestaltet, dass eine Analyse nicht mehr möglich ist. Das Geheimnis bleibt ein solches. Trotzdem, alle Teilquadrate sind nach wie vor magische Quadrate der 5. Ordnung mit der magischen Summe von 565. Die nächste Abbildung zeigt das veränderte 15er Quadrat.
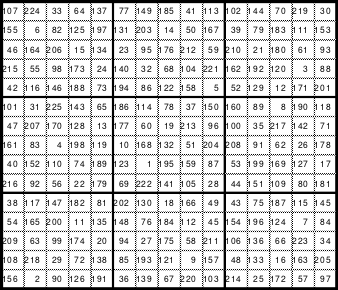
Anfangs waren alle Teilquadrate pandiagonal, was das Versetzen einzelner Spalten und/oder Zeilen ermöglichte. So konnten die ersten Veränderungen vorgenommen werden. Anschließend hat Mag das Rautenprinzip und Flächenprinzip unterschiedlich, einzeln oder kombiniert angewendet, um die Teilquadrate weiter zu verändern. Da die Teilquadrate alle gleich groß sind, hat Mag diese auch ungeordnet zusammenfügen können. Das Ergebnis ist ein Quadrat der 15. Ordnung mir der magischen Summe von 1695, bestehend aus 9 Quadraten der 5. Ordnung mit den einheitlichen magischen Summen von 565. Sie können sich davon überzeugen, dass eine Struktur des Aufbaus dieser Teilquadrate nicht mehr zu erkennen ist.
(Die lineare Unterteilung dient lediglich einer besseren Kontrolle zu den Ausführungen und darf normal nicht vorhanden sein!)
Die Prinzipien zur Bildung von Chaosquadraten sind aber nicht nur dazu da, um die Strukturen von Quadraten aufzulösen, sondern sie leisten auch gute Dienste bei der Bildung von Quadraten.
Damit schließt Mag den Abschnitt über die Chaosquadrate ab. Er hofft, dass er die Zweckmäßigkeit derartiger Manipulationen ausreichend begründet hat.
6 Hexen 1x1
6.1 Vorbemerkungen
6.1.1 Einführung in das “Hexen 1 x 1”
Das “Hexen 1 x 1” ist das Kernstück von Mag´s Beschreibungen. Es befasst sich mit der Rechenkunst mit magischen Quadraten. Dabei hat sich Mag stets bemüht die Ausführungen mit kleineren Zahlen zu gestalten. So können die Lösungen der gestellten Aufgaben besser verstanden werden. Allerdings ist das nicht immer der Fall. Viele Beschreibungen aus dem “Großen Hexeneinmaleins” seines nicht veröffentlichen Buches hat Mag in diese Ausführungen einfließen lassen. Dabei geht es um den Einsatz von größeren Zahlenvorgaben. Eine Überarbeitung unter Verwendung kleinerer Vorgaben war wegen eines zu hohen Aufwandes nicht immer gegeben. Weiter ist zu beachten, dass bei größeren Quadraten auch größere Zahlen zum Einsatz kommen müssen. So ist schon die magische Summe eines Quadrates der 8. Ordnung 260 und beim Quadrat der 5. Ordnung immerhin noch 65.
Mag möchte mit seinen Darlegungen Ihr Interesse wecken und den Fans der magischen Quadrate Anregungen geben. Er will Sie nicht unbedingt zum Rechenkünstler animieren. Sollte bei Ihnen doch der Wunsch geweckt werden, sich als Rechenkünstler zu betätigen, würde sich Mag freuen, gibt aber dazu einigen Bedenken und Anregungen, die Sie in Ihre Gedanken einfließen lassen sollten.
Als Rechenkünstler sollten Sie über eine gewisse Ausrüstung verfügen. Schwerpunkt dabei ist eine Tafel entsprechender Größe. Auch wenn diese falt- und klappbar gestaltet ist, muss sie auch transportiert werden. Des Weiteren ist ein geeigneter Tisch notwendig, um dort Ablagen zu ermöglichen. Ein Aufwand, dem nur wenige Möglichkeiten der Nutzung gegenüberstehen.
Auch der geistige Aufwand ist nicht unerheblich. Selbst wenn man nur mit kleinen Quadraten, der 3. oder 4. Ordnung arbeitet, so muss das Quadrat in seiner Struktur und Zahlenfolge total beherrscht werden. Auch die Rechenleistungen können, je nachdem mit welcher Zahlengröße gearbeitet wird, erheblich sein. Und das alles für wenige Auftrittsmöglichkeiten? Denn das Interesse des Publikums an derartigen Vorführungen ist begrenzt, viele fühlen sich überfordert. Nicht nur deshalb müssen Sie stets höflich und zuvorkommend ihrem Publikum gegenüber sein.
Bei der Kleidung verbieten sich Artisten-, Flimmer- oder Zauberbekleidung. Schließlich Zaubern Sie nicht und wenden auch keine Tricks an, auch wenn Sie rationelle Rechenmethoden nutzen. Kleiden Sie sich seriös, auch wenn das heutzutage nicht mehr in ist. Wenn Sie mit Tafelkreide arbeiten, dann sollte die Kleidung nicht zu dunkel sein. Kreideflecke sind nämlich nicht gerade schön.
Wenn Sie an der Tafel arbeiten, dann stellen Sie sich nicht unbedingt mit dem Rücken zum Publikum, sondern versuchen Sie wenigstens halb seitlich zu stehen, auch wenn dann das Anschreiben schwieriger ist. Versuchen Sie Ihre Aktionen nicht mit Ihrem Körper zu verdecken, das Publikum will sehen was Sie machen. Aus diesem Grund versuchen Sie auch ab und zu die Seite zu wechseln, damit die auf der anderen Seite sitzenden Personen auch mal Ihre Aktionen verfolgen können.
Sprechen Sie laut und deutlich, damit Ihre Zuschauer auch verstehen was Sie meinen. Dazu ein kleiner Tipp, richten Sie ihr Sprechen an die Personen die sich am weitesten von Ihnen befinden. Das veranlasst Sie automatisch dazu lauter zu sprechen.
Benutzen Sie keine Wörter aus der Zauberei, wie “Zauberquadrat” oder “Zauberzahl”, wenn ein magisches Quadrat oder die magische Summe meinen. Derartige Begriffe sind leider selbst im Internet zu finden. Mag spricht auch weniger von einem Rechenkunststück, sondern eher von einem Rechenexperiment. Experimente sind Versuche die auch mal ein negatives Ergebnis bringen. Damit suggeriert Mag die Zuschauer unterschwellig, dass das Experiment auch mal nicht das gewünschte Ergebnis bringt. Derartige Hinweise könnten noch weitere folgen, Mag betrachtet diese jedoch als ausreichend, um Sie zum Überdenken anzuregen. Sollte es immer noch Ihr Wunsch sein, ein kleines Programm als Rechenkünstler aufzubauen, so gestalten Sie ihr Programm abwechslungsreich. Höchstens 3-mal ein magisches Quadrat und dazwischen andere Rechenkunststücke die Sie kennen und können. Falls letzteres nicht der Fall sein sollte und das Experiment “Das Superhirn” für sie zu schwer ist, Mag hat zwei einfache Experimente und eine heitere Rechnerei dem Anhang unter “6.Zwischendurch” beigefügt (“6 aus 3”, “Durchstochenes” und “Kleiner Spaß”).
Mag hofft, Ihnen mit diesen Bemerkungen nicht den Mut genommen zu haben. Es müssen ja nicht gleich die Bretter der weltberühmten Bühnen sein, ein Auftritt unter anderem im kleinen Kreis der Familie, oder vor Freunden, ist doch auch was Gutes, zumal dann keine großen Ausrüstungen erforderlich sind. Es genügt ein großer Zeichenblock und ein Faserstift und los geht es. Ein intimer Kreis hat auch den Vorteil, dass schon einfache Experimente mit kleinen Zahlen gezeigt werden können. Die Erwartungen Ihrer Zuschauer sind nicht so hochgesteckt und sie sind auch verständnisvoller, wenn mal etwas schief geht.
Doch nun genug damit!
Schließlich geht es bei den magischen Quadraten um mehr als mit diesen vor einem Publikum zu agieren. Das ist nur ein kleiner Teil dieses sehr umfangreichen Gebietes. Das werden Sie erkennen, wenn Sie sich mit der Materie intensiv beschäftigen. Mag hat die Ausführungen vor allem für die Freunde der magischen Quadrate und für die, die es noch werden könnten, geschrieben. Für jene, deren Hobby die Beschäftigung mit den magischen Quadraten ist. Es sind nicht wenige die diesem Hobby nachgehen, sie sind nur wenig bekannt, da sie selten in der Öffentlichkeit in Erscheinung treten. Sie haben sich auch noch nicht zu einem Verein zusammengefunden. Mag hofft das seine Ausführungen manchen Fan Anregung und neue Erkenntnisse vermittelt und Weitere für die faszinierende Welt der magischen Quadrate begeistern kann.
Geeignete Quadrate
Generell können mit allen magischen Quadraten Rechenexperimente vorgenommen werden. Doch für Vorführungen sind nur wenige geeignet. So scheiden alle Quadrate größer Ordnungszahl 5 aus. Diese erfordern nicht nur eine große Tafel, sondern auch mehr Zeit um das Quadrat zu gestalten, was sich in der Regel negativ auf die Zuschauer auswirken kann. Auch ist es nicht möglich mit diesen zu arbeiten, weil deren Struktur des Aufbaus nur bedingt bestimmten Regeln folgt und das bedeutet, dass die Zahlenfolge in den Zellen auswendig gelernt werden müssten. Das trifft besondere auf die einfachgeraden Quadrate der 6., 8. und 10. Ordnung zu. Aber auch die so genannten Triquadrate, insbesondere das 9er Quadrat, eignet sich kaum, weil diese nicht pandiagonal sind.
Das noch gut geeignete Quadrat ist das Pentaquadrat, ein Quadrat der 5. Ordnung. Dieses ist pandiagonal und 100%ig homogen. Aus diesem Grund hat es Mag noch als geeignet eingeschätzt, obwohl es eigentlich auch schon zu groß ist. Am häufigsten wird das Topquadrat der 4. Ordnung gezeigt, es ist pandiagonal, jedoch nur Teilhomogen. Welche Probleme im Ausnahmefall dadurch entstehen können, wird bei der Behandlung der Rechenkunst mit dem Topquadrat erläutert. Auch wenn Mag der Meinung ist, dass sich die großen Quadrate nicht für Vorführungen eignen, hat er Beispiele für Quadrate der 7., 8. und 9. Ordnung beschrieben. Diese sind jedoch nur sehr schwer vorzuführen. Bereits die Erläuterungen sind ohne Vorkenntnisse kaum nachvollziehbar.
Auch in seinen Excel-Anwendungen geht er bis zu Quadraten der 20. Ordnung. Er will sich ja nicht nur an die wenden, die wissen wollen wie das mit den Berechnungen geht, um es evtl. selbst vorzuführen, sondern an einen viel breiteren Kreis von Interessenden. Die gezeigten Beispiele mit kleinen Quadraten können in gleicher Weise auf alle Quadratgrößen angewendet werden. Dabei sind allerdings oft viel höhere Anforderungen an den Anwender zu stellen. Auch sind dann manchmal andere Verfahren besser geeignet.
Die Vorgaben
In der Regel geht es um die Erstellung eines magischen Quadrates, bei dem die Zuschauer eine Zahl als magische Summe vorgeben, oder eine Zahl genannt wird, die in eine bestimmte Zelle eingesetzt werden soll. Im ersten Fall ist ein Quadrat zu bilden, bei dem die Summen aller Reihen der vorgegebenen magischen Summe entsprechen.
Im zweiten Fall muss die magische Summe ermittelt werden, die über das Quadrat geschrieben wird. Anschließend sind alle Zellen mit Zahlen auszufüllen die als Summen der magischen Summe entsprechen. Bei einer Doppelvorgabe können die magische Summe und eine Zellenzahl, oder auch 2 Zellenzahlen vorgegeben werden. Die Lösungen dafür sind natürlich schwerer. In der Regel begnügt man sich auf die Nennung einer Zahl und die Zelle, in die die Zahl eingesetzt werden soll als Doppelvorgabe. In Ausnahmefällen sind die Angaben des Zuschauers an Listen oder Zahlenkarten gebunden. Das ist z. B. bei den “Primzahlenquadraten” und dem “Austauschquadrat” der Fall. Diese Vorführungen sind Ausnahmedarbietungen.
Die gewürfelte Vorgabe
Für den Anfang dürfte die richtige Einordnung des Endrestes schwierig sein, besonders, wenn das Quadrat nicht homogen ist. Die Vermeidung eines Endrestes ist dann wünschenswert. Es ist aber bedenklich, wenn der Vorführende um eine durch 3, 4 oder 5 teilbare Vorgabezahl bittet. Mag gibt einen Tipp, wie man eine Vorgabe ohne Endrest erreichen kann, was natürlich nur bei Vorführungen im kleinsten Kreis, sozusagen am Tisch, zulässig ist.
Grundlage ist die Regel, dass jedes Produkt einer Multiplikation durch die Zahlen dividiert werden kann, die ein Faktor (Multiplikand) bei der Bildung des Produktes waren. Verständlicher heißt das, multipliziert man eine Zahl mit dem Faktor x, so ist das Ergebnis auch durch x teilbar. Der Akteur bittet die Gäste Einfluss auf die Bildung einer größeren Zahl zu nehmen. Er überreicht dem 1. Gast einen Würfelbecher mit einem Würfel und Schreibzeug mit der Bitte, eine Zahl zu würfeln und aufzuschreiben.
Der nächste Gast soll ebenfalls eine Zahl würfeln und das Ergebnis des Vorgängers damit multiplizieren. Auch der nächste Gast soll würfeln und das Ergebnis seiner Vorgänger mit der gewürfelten Zahl multiplizieren. So wird verfahren bis den Akteur glaubt, dass eine ausreichend große Summe erreicht ist. Er lässt sich das Ergebnis nennen und prüft es auf Richtigkeit. Er kann sehr schnell erkennen, ob ein Fehler vorliegt.
Das Ergebnis ist:
durch 2 teilbar, wenn ein gerade Zahl in die Berechnung eingeflossen ist.
das Ergebnis muss eine gerade Zahl sein.
durch 3 teilbar, wenn eine 3 oder 6 gewürfelt wurde.
die Quersumme muss durch 3 teilbar sein,
durch 4 teilbar, wenn eine 4- oder 2-mal eine gerade Zahl Bestandteil der Berechnung ist,
die Zahl aus den beiden letzten Ziffern muss durch 4 teilbar sein.
durch 5 teilbar, wenn eine 5 gewürfelt wurde.
die letzte Ziffer muss eine 5 oder 0 sein.
durch 8 teilbar, wenn 2-mal die 4, eine 4 und eine gerade oder 3-mal eine gerade
Zahl in die Berechnung eingegangen sind.
die Zahl aus den letzten 3 Ziffern muss durch 8 teilbar sein. Ist die hunderter Ziffer
eine gerade Zahl, so müssen nur die letzten 2 Ziffern durch 8 teilbar sein.
Der Akteur muss nur darauf achten, dass Werte gewürfelt wurden, die eine gewünschte Teilbarkeit sichern. Er kann an dieser Stelle abbrechen oder auch weiter würfeln lassen.
Bei der Abhandlung zum Miniquadrat wird Mag weitere Möglichkeiten zur Bildung geeigneter Vorgaben der magischen Summe nennen, die sich auch für Auftritte im größeren Rahmen eignen.
Das Basisquadrat
Das Basisquadrat, auf das in den Beschreibungen öfters Bezug genommen wird, ist das Quadrat in dem lückenlos alle Zahlen von 1 bis n enthalten sind. Dabei ist n das Quadrat der Ordnungszahl (O2). Es wird auch oft als Grundquadrat bezeichnet.
Die Berechnung
Es gibt mehrere Rechenwege um zum gewünschten Ergebnis zu kommen. Sie sind unterschiedlich in den Anforderungen zur Rechenleistung und unterschiedlich im Stil, die die Attraktivität der Vorführung beeinflussen. Ziel ist es, die Rechenoperationen so zu gestalten, dass eine Regel nicht erkannt werden kann. Zum anderen soll sie leicht beherrschbar sein. Mag geht auf 2 Methoden ein, die Multi- und die Duomethode.
Mag wendet bei seinen Berechnungen hauptsächlich die Duomethode an. Sie ist leichter zu handhaben. Die Erläuterung zu diesen beiden Methoden sind in den folgenden Dateien “Die Multimethode” und “Die Duomethode” zu finden und sollte ausgewertet werden, denn in den weiteren Beschreibungen werden nicht immer detaillierte Erläuterung zu den Berechnungen gemacht.
Grenzüberschreitung
Insbesondere beim Springen innerhalb eines Quadrates kommt es dazu, dass man an die äußere Begrenzung des Quadrates kommt. Es ist allgemein bekannt, dass in diesem Fall von der gegenüber liegenden Grenze weiter gegangen wird. Ebenso verhält es sich bei der senkrechten Bewegung. Kommt man unten an, geht es von oben aus weiter und umgekehrt. Etwas komplizierter ist es, wenn bei einem Sprung beide Grenzen überschritten werden müssen. Es ist in diesem Fall auch möglich, innerhalb des Quadrates zu bleiben, indem man entgegengesetzt zieht, wobei die Anzahl der Zellen, um die weiter gegangen wird, die Ordnungszahl abzüglich der Schritte des Sprunges ist.
Zum Beispiel ein Quadrat der 5. Ordnung:
eingeordnet ist, kann es schwierig werden. Das ist z. B. bei der Erstellung des 8er Duoquadrates der Fall. In diesen Fällen kann auch rückwärts gesprungen werden. Das wäre in diesem Fall, statt 2 nach rechts, 3 nach links (Ordnungszahl 5 - 2) und statt 1 nach unten, 4 nach oben (Ordnungszahl 5 - 1) und man gelangt zur Zelle 10.
Hohe Schule
Den Begriff “Hohe Schule” verwendet Mag nicht nur für schwierig zu bildende Quadrate an, sondern auch für die Art und Weise der Eintragung der Zellenzahlen, wobei die Eintragung der Zellenzahlen zeilenweise von links nach rechts erfolgt. Dieser Stil der Vorführung ist einfach eleganter und für den Zuschauer weniger durchschaubar. Allerdings auch etwas schwieriger, wobei dieser Stil bei einigen Darbietungen unvermeidbar ist. Mag geht bei seinen Ausführungen zu den einzelnen Quadraten auf diese Form der Erarbeitung ein.
Mag hat die Experimente, die er als schwierig einschätzt mit einem Stern (*) gekennzeichnet und Experimente mit den höchsten Schwierigkeitsgraden mit zwei Sternen (**).
Der Endrest
Ein Endrest entsteht, wenn bei der Division des Restes durch die Ordnungszahl kein ganzzahliges Ergebnis entsteht.
Der Endrest ist oft nicht vermeidbar und ist das Übel bei der Quadratbildung. Der Endrest ist in der Regel kleiner als die Ordnungszahl und kann deshalb nicht allen Zellen zugeschlagen werden. Er kann von einfach, über schwierig bis unmöglich eingearbeitet werden. Dabei gilt grundsätzlich, dass der Endrest so in das Quadrat eingeordnet werden muss, dass er in jeder Zeile, Spalte und Diagonalen, möglichst auch der gebrochenen, wirksam wird, jedoch nur 1 Mal.
Die Wahrscheinlichkeit, dass ein Endrest entsteht und dessen Größe, wächst mit der Zunahme der Ordnungszahl. Am einfachsten ist die Einordnung des Endrestes bei den 100%ig homogenen Quadraten. Das sind die Primquadrate. Hier werden alle Zahlen des letzten Blockes zusätzlich um den Endrest erhöht.
Das kann auch beim Topquadrat so erfolgen, auch wenn es nicht ganz 100%ig ein homogenes Quadrat ist. Hier treten die Probleme nur in Ausnahmefällen auf und zwar bei Vorgabe einer ungeraden magische Summe und einer Zelle in die die erste Zahl eingesetzt werden soll. Die Schwierigkeiten können meist umgangen werden. Wie, zeigt Mag in den einzelnen Erläuterungen.
Noch eine Randbemerkung dazu: Es ist auch möglich den Endrest anderen Blöcken zuzuordnen. Das bedingt aber, dass der Endrest kleiner als der Multiplikator bzw. der Schlüsselzahl ist. Anderenfalls kann es zu doppelten Zahlen kommen.
Schwierig ist die Einordnung des Endrestes bei nicht homogenen Quadraten. Das sind vor allem die einfach geraden Quadrate, wie das 6er, 10er usw. und die ungeraden Quadrate, soweit sie keine Primquadrate sind. Zum Teil sind die Zahlen des größten Blockes so verteilt, dass sie je eine Reihe im Quadrat abdecken. Ist das nicht der Fall, so kann man versuchen durch Umstellungen das zu erreichen, was nicht immer gelingt. Wenn es gelingt, so gibt es meist keine Regel, diese bei einer Vorführung zu finden. Insbesondere wegen dieser Probleme hat Mag derartige Quadrate aus dem Hexen 1x1 ausgeschlossen.
Völlig unmöglich ist die Einordnung des Endrestes in ein 3er Quadrat, dem Lo-Shu-Quadrat. Es ist nur Teilhomogen. Auch können keine 3 Zellen gefunden werden, die die Bedingungen, in jeder Reihe wirksam zu werden, erfüllen. Hier kann nur mit magischen Summen gearbeitet werden, die durch 3 teilbar sind, weil dann kein Rest entsteht. Wie das erreicht werden kann, beschreibt Mag in den weiteren Abhandlungen.
Die Schlüsselzahl
Besonders bei Anwendung der Multimethode werden die neuen Zahlen für die Zellen in der Regel durch Multiplikationen und/oder Addition mit einer Schlüsselzahl berechnet. Bei der Bildung der Schlüsselzahl ist zu beachten, dass solche mit einer geraden Zahl ungünstig sind, denn dann werden alle Zahlen des Quadrates eine gerade Endziffer haben. Auch die 0 (Null) oder 5 sollten ausgeschlossen werden. Ergibt die Berechnung der Schlüsselzahl einen der genannten ungünstigen Fälle, so reduziert man diese um die Ordnungszahl und erhöht dafür den Summanden.
Bei der Duomethode, wo die Schlüsselzahl nahezu frei gewählt werden kann, sollte diese so gewählt werden, dass sie die negativen Fälle ausschließt und gleichzeitig ein leichtes Rechnen ermöglichen. Mag versucht nach Möglichkeit Schlüsselzahlen mit der Endziffer 9 zu bilden. Hier ist eine Regel nicht so schnell erkennbar. Mag verwendet meist eine durch 9 teilbare Schlüsselzahl. Diese sind fast genau so leicht zu handhaben wie die Schlüsselzahlen wo die letzte Ziffer eine 9 ist. Diese Schlüsselzahlen sind sinnvoll, wenn es in einigen Experimenten um die Vermeidung von doppelten Zahlen geht.
Gut geeignet sind auch Schlüsselzahlen mit den Endziffern 3 oder 7, wobei eine bessere Zahlenverteilung und nur kleinere Zahlenlücken entstehen. Mag verwendet bei seinen Berechnungen neben den genannten mit der Endziffern 9, 7 oder 3 auch Schlüsselzahlen die das ein- und mehrfache von 9 sind. Mit diesen Schlüsselzahlen zu rechnen bedeutet keine nennenswerte erhöhte Rechenleistung. Dazu einige Beispiele:
Schlüsselzahl: 9 = 1 * 9 = 9 = 10 - 1
18 = 2 * 9 = 18 = 20 - 2
27 = 3 * 9 = 27 = 30 - 3
36 = 4 * 9 = 36 = 40 - 4 und größere Schlüsselzahlen
108 = 12 * 9 = 112 = 110 - 2 also nahezu wie 109
198 = 22 * 9 = 198 = 200 - 2
Sicher stellen Sie die Frage wozu derartige Schlüsselzahlen?
Bei einer Zahlenvorgabe für 2 Zellen, kann es vorkommen, dass diese eine zu kleine Differenz haben um die gewohnten Rechnungen durchzuführen. Will man keine Änderung einer Zahl verlangen, so muss mit den Vorgaben gearbeitet werden. Diese können auch zu klein sein, um bis zu 8-mal 9 bzw. 8mal 7 abzuziehen um die Zahl für die Zelle 1 zu ermitteln. In diesen Fällen kann z. B. auf das Duo 8/9 oder 5/12 zugegriffen werden. Dabei kann es zu doppelten Zahlen kommen, was ja unzulässig ist.
Dazu eine einfache mathematische Regel, die Mag nicht weiter beweisen muss. Von der Richtigkeit können sich Zweifler durch Versuche überzeugen.
Wenn die Differenz zwischen 2 Zahlen nicht durch die Schlüsselzahl teilbar ist,
werden keine doppelten Zahlen entstehen, wenn diese um das 1- oder mehrfache
der Schlüsselzahl erhöht oder vermindert werden.
Diese Regel nutzt Mag, indem er möglichst Schlüsselzahlen einsetzt, die das 1- oder mehrfache von 9 sind.
Um zu prüfen. ob die Entstehung doppelter Zahlen möglich ist, wird geprüft ob die Differenz der beiden Vorgaben durch 9 geteilt werden kann. Das wird selten der Fall sein. Nur wenn dieses zutrifft kann es zu doppelten Zahlen kommen und nur dann sollte um eine andere Vorgabezahl gebeten werden, oder man wählt eine andere Schlüsselzahl z. B. die 7.
Zwar ist es möglich, dass es zu einer dichten Annäherung von Zahlen kommen kann, wobei die Differenz auch nur noch 1 sein kann. Doppelte Zahlen sind jedoch ausgeschlossen und die eventuell fast gleichen Zahlen müssen in Kauf genommen werden.
Mag hat öfters darauf hingewiesen, dass die Schlüsselzahlen eine ungerade Zahl sein sollte. Dem entgegen hat er jedoch Schlüsselzahlen wie 18, 36 u. a. für den Einsatz angegeben. Gerade Schlüsselzahlen wie auch 6, 4, 8 usw. können verwendet werden, wenn bei einer Doppelvorgabe, oder bei der Anwendung der Duomethode die beiden Zahlen nicht einheitlich gerade oder ungerade sind. In diesen Fällen ist der Einsatz von geraden Zahlen evtl. sogar vorteilhaft, weil dann keine gleichen Zahlen entstehen können.
Nachbetrachtungen
Bei den Beschreibungen zur Berechnung der einzelnen Quadrate hat Mag versucht, sich nur auf das Wesentliche zu konzentrieren. Eventuelle Randprobleme oder Hinweise zu einer erweiterten oder verbesserten Darbietung, hat Mag als “Nachbetrachtung” beschrieben.
6.1.2 Die Multimethode
Die Multimethode ist schwerer zu handhaben als die Duomethode. Sie kann aber bei kleinerem Quadrat und kleineren Vorgaben durchaus die günstigere sein, da es bei dieser Methode zu einer besseren Zahlenverteilung kommt. Bei großen Quadraten, oder größeren Vorgaben ist sie aber weniger geeignet, da höhere Anforderungen an die Rechenleistungen gestellt werden. Auch können berechnete Werte in der Regel nicht sofort in eine Zelle geschrieben werden, da sich die Zellenzahlen aus mehreren Werten (Produkt, Summand und evtl. Endrest) zusammensetzen.
Die einzelnen Rechenschritte bei der Multimethode sind:
Die Vorgabe der magischen Summe wird durch die magische Summe des Basisquadrates dividiert und erhält den Multiplikator, wobei ein Rest verbleibt.
Dieser Rest wird durch die Ordnungszahl dividiert und man erhält ein Summand und einen Endrest.
Alle Zellenzahlen des Basisquadrates werden mit dem Multiplikator multipliziert und der Summand dazugerechnet.
Der Endrest muss so in die Zellen eingeordnet werden, dass er in allen Zeilen, Spalten und Diagonalen, möglichst auch in den gebrochenen Diagonalen, wirksam wird und zwar nur einmal.
Mag hat diese Methode wegen der präziseren Ergebnisse bei der Berechnung der Quadrate in der Excel-Datei “Multiquadrate”, im Teil “Helfer PC”, eingesetzt.
Beispiele mit dem Topquadrat, dessen Ordnungszahl 4 und die magische Summe 34 ist.
Beispiel 1: Summenvorgabe 261.
Ermittlung des Multiplikators = 261/34 = 7, Rest 23
“ “ Summanden = 23/4 = 5, Endrest 3
Berechnung der Zahl für Zelle 1 = 1*7+5 = 12
2 = 2*7+5 = 19 usw. bis Zelle 12
12 = 12*7+5 = 89
die Zahlen des 4. Blockes müssen zusätzlich um den Endrest erhöht werden.
Berechnung der Zahl für Zelle 13 = 13*7+5+3 = 99
14 = 14*7+5+3 = 106 usw. bis zur Fertigstellung
Das fertige Quadrat, rechts, ist magisch mit der vorgegebenen Summe von 261. Die Zahlen von 12 bis 120 sind gleichmäßig verteilt.
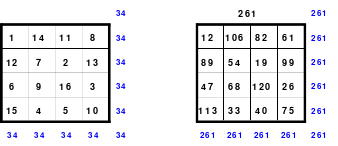
Die erforderlichen Rechenoperationen sind einfach und lösbar.
Beispiel 2: Summenvorgabe 5879
Ermittlung des Multiplikators = 5879/34 = 172, Rest 31
“ “ Summanden = 31/4 = 7, Endrest 3
Berechnung der Zahl für Zelle 1 = 1*172+7 = 179
2 = 2*172+7 = 351 usw. bis Zelle 12
12 = 12*172+7 = 2071
die Zahlen des 4. Blockes müssen zusätzlich um den Endrest erhöht werden.
Berechnung der Zahl für Zelle 13 = 13*172+7+3 = 2246
14 = 14*172+7+3 = 2418 usw. bis Fertigstellung
Auch dieses Quadrat ist ein magisches mit der richtigen Vorgabesumme von 5879. Die Zahlen sind von 179 bis 2762 gleichmäßig verteilt.
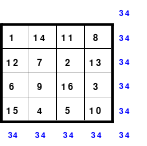
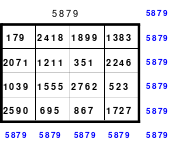
Die erforderlichen Berechnungen sind wesentlich schwerer, aber noch mittels Kopfrechnens lösbar. Jedoch dürften die Zeiten zu deren Berechnung entschieden größer sein und ermöglicht kaum ein gewünschtes zügiges Abarbeiten.
Nach dieser Methode können praktisch Quadrate aller Größen gestaltet werden.
Hinweise
In den beiden Beispielen hat Mag jede Zahl für die Zellen einzeln berechnet. Das war bewusst gemacht, damit das Prinzip der Multimethode gut erkannt wird.
In der Praxis wird diese Form der Berechnung angewendet, wenn der Zahleneintrag zeilenweise erfolgt. Bei der Eintragung nach der natürlichen Zahlenfolge (1, 2, 3 usw.), so wie in den Beispielen, ist es einfacher, wenn zur vorherigen Zahl lediglich die Schlüsselzahl addiert wird. Dabei darf kein Fehler gemacht werden, denn dieser würde bis ans Ende mitgeschleppt werden und ist nur noch schwer zu finden, was eine Korrektur sehr erschwert. (Einem Rechenkünstler kann kein Fehler zugestanden werden. Er muss fehlerfrei sein!)
Es kann selten, aber möglicherweise zu ungünstigen Multiplikatoren kommen. Zum Beispiel solche mit einer letzten Ziffer 0 oder 5. In diesem Fall werden alle Zahlen gleiche Endziffern, bestenfalls 2 gleiche Endziffern haben. Daran ändert der Zuschlag des Restes auch nichts.
In diesen Fällen ist es sinnvoll den Multiplikator um 1 zu reduzieren, wodurch sich allerdings der Rest zusätzlich um 34 erhöht.
Schlussfolgerung
Die Anwendung der Multimethode ist für kleine Quadrate und kleinen Summenvorgaben durchaus brauchbar. Bei einer kleineren Zahlenvorgabe für eine Zelle schätzt Mag diese sogar günstiger als die Duomethode ein.
Dazu ebenfalls ein Beispiel:
Zahlenvorgabe
Es soll ein magisches Quadrat der 5. Ordnung gebildet werden, wobei eine Zahlenvorgabe von 67 gemacht wird.
Mag schreibt die Vorgabe in die 2. Zelle der 3. Zeile. (siehe hervorgehobene 67)
Nach kurzer Überlegung schreibt er über das Quadrat die Zahl 605.
Anschließend trägt er in alle Zellen unterschiedliche Zahlen ein, bis alle Zellen eine Zahl enthalten.
Das so entstandene Quadrat ist magisch, pandiagonal und die Reihensummen entsprechen der von Mag anfangs über das Quadrat geschrieben 605.
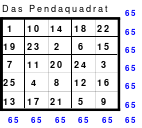
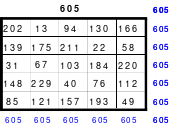
Lösung
Mag schreibt die Vorgabe in eine beliebige Zelle, hier die genannte. Er hätte auch die Zelle von einem Gast wählen lassen können. Da das Pentaquadrat ein pandiagonales Primquadrat ist, kann die gewählte Zelle jede der 25 möglichen sein. Im Beispiel wird es die Zelle 7 sein, denn Mag dividiert die Vorgabe durch 9, die er als Schlüsselzahl bestimmt hat, und erhält 7 als Zelle und einen Rest von 67-7*9 = 67-63 = 4. Aus diesen Zahlen errechnet er die magische Summe. Da die magische Summe des Basisquadrates 65 ist, wird die magische Summe = 65*9 = 650-65 (9 ist 10-1) >> 585+5*4 = 585+20 = 605. (Dabei ist 5 die Ordnungszahl und 4 der Rest, der ja in jeder Zelle wirksam wird.)
Die gefundene Summe wird über das Quadrat geschrieben.
Bei der folgenden Eintragung der Zellenzahlen ist einiges zu beachten.
Es ist vom Vorteil, als erstes die niederen Zellen des Blockes auszufüllen. Das ist im vorliegenden Fall nur die Zelle 6 als 1. des 2. Blockes. Diese findet man durch einen Rückwärtssprung. Das ist 1 nach oben und 2 nach links, oder auch 1 nach oben und 3 nach rechts. Dort wird die um die Schlüsselzahl verringerte Zahl aus Zelle 7 eingesetzte. Das ist 67-9 = 58.
Nun können die aufsteigenden Zellen mit Zahlen belegt werden.
Das ist von Zelle 7 aus, 2 rechts, 1 nach unten zur Zelle 8, in die 67+9 = 76 kommt. Weiter 2 nach rechts, 1 nach unten, zur Zelle 9 in die 76+9 = 85 geschrieben wird und weiter zur Zelle 10 mit der Zahl mit der Zahl 94.
Wenn jetzt wieder 2 nach rechts und 1 nach unten gegangen wird, stößt man auf eine Zelle, die bereits eine Zahl enthält, nämlich die Zelle 6, die 1. im Block. (Jetzt wissen Sie, warum als erstes die absteigenden Zellen des aktuellen Blockes bearbeitet werden sollen.) Das bedeutet, dass der Block fertig ist und zum nächsten gegangen werden muss. Das ist 2 nach unten zur Zelle 11 in die die Zahl 94+9 = 103 eingesetzt wird.
So werden alle aufsteigenden Zellen bis zur Zelle 25 abgearbeitet. Aber Achtung! auch wenn man von Zelle 25 nicht 2 nach rechts und 1 nach unten gehen kann, weil
dort eine Zahl bereits steht, kann man nicht wieder 2 nach unten gehen, auch wenn das möglich wäre. Denn die Zelle 1 enthält keine Zahl. Deshalb sollte man die Zahl für Zelle 25 mit 25*9 = 225 + Rest 4 =229 berechnen und gut merken. Wenn diese Zahl erreicht wird, weiß man, dass alle aufsteigenden Zellen fertig sind.
Es ist bekannt, dass nicht nur die Zahlen eines Blockes einen Ring darstellen, sondern auch die Blöcke selbst. Das bedeutet, dass sich von Zelle 25 aus 2 nach unten der 1. Block mit der Zelle 1 befindet.
In die so gefundene Zelle 1 wird einfach die Schlüsselzahl + Rest, das ist 9+4 = 13 geschrieben. Die restlichen Zellen können nun wieder als aufsteigende Zellen abgearbeitet werden, bis alle Zellen ausgefüllt sind und das Quadrat damit fertig ist.
Mag hat damit gezeigt, dass die Multimethode auch ein einfaches Rechnen ermöglicht und nur bei großen Vorgaben und großen Quadraten Schwierigeres Rechnen erforderlich wird. Hier bietet sich die Duomethode an, da hier die Rechenoperationen einfacher sind, was allerdings bei kleinen Vorgaben nicht unbedingt der Fall ist.
Mag hat für das letzte Beispiel das Pentaquadrat, ein Primquadrat der 5. Ordnung gewählt, weil dieses Quadrat nach einer einheitlichen Ordnung aufgebaut ist. Das ermöglicht ein einfaches Finden der nächsten Zellen. Das Quadrat muss nicht auswendig beherrscht werden.
Das ist beim ebenfalls pandiagonalen Topquadrat nicht der Fall. Hier muss der Aufbau des Quadrates auswendig erlernt werden. Wenn das erlernt ist, so kann auch die Eintragung zeilenweise entsprechend der hohen Schule erfolgen. Auch wenn eine Zellenvorgabe erfolgt, d. h. auch beim Topquadrat ist der Start nicht an eine bestimmte Zelle gebunden.
Ansonsten ist die Berechnung die gleiche wie beim Pentaquadrat, allerdings mit den Parametern des Topquadrates
6.1.3. Die Duomethode
Mag wendet bei seinen Berechnungen hauptsächlich die Duomethode an. Sie ist viel leichter zu handhaben. Es entfällt zum Beispiel die Berechnung eines Summanden und dessen Addition zu den Zellenzahlen, sodass nur die Multiplikation angewendet werden muss. Es wird nur der Endrest anfallen. Dieser ist immer kleiner als die Ordnungszahl. Bei den geraden Quadraten wird der Anfall eines Endrestes sogar auf die Hälfte reduziert. So ist er beim Einsatz des Topquadrates maximal 1 groß. Auch kann der Multiplikator, die Schlüsselzahl, besser an eine leichtere Berechnung angepasst werden, da sie nahezu frei wählbar ist.
Ein großer Vorteil bei der Duomethode ist, dass hier selbst bei sehr großen Vorgaben mit wesentlich kleineren Zahlen gerechnet wird. Es sind auch viel weniger Rechenoperationen notwendig.
Auch müssen weitaus weniger Zahlen im Gedächtnis behalten werden, da die meisten durch Division gebildet werden und folglich von links nach rechts abgearbeitet werden und dabei fortlaufend in die Zelle oder über das Quadrat geschrieben werden können. Auch sind es weniger Parameter die zu merken sind.
Einzelheiten zu dieser Rechentechnik erfahren Sie bei der praktischen Anwendung in den Beispielen.
Die Zahlen der magischen Quadrate können als Duoreihen dargestellt werden. Dabei unterscheiden sich die geraden von den ungeraden Quadraten. Mag wird seine Erläuterungen deshalb zu den Top- und Pentaquadrat trennen. Die dazu gehörigen Duoketten sind die Grundlage für die Ausführungen.
Zum Topquadrat
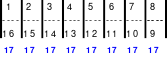
Da das Topquadrat ein Quadrat mit gerader Ordnungszahl ist, gibt es keine mittlere Zahl. Die Mitte wird durch das Duo paar 8/9 gebildet.
Alle Duos haben die einheitliche Summe von 17. Das ist die Hälfte der magischen Summe des Topquadrates von 34. Jedes Duo belegt 2 Zellen und das ist die Hälfte der 4 Zellen je Reihe im Topquadrat.
Schlussfolgerung: Die Summe jedes Duopaares entspricht der halben magischen Summe des Topquadrates und umgekehrt ergibt die Verdopplung eines Duopaares die magische Summe.
In der Praxis wird die Duosumme in die Zellen 16 und 1 eingesetzt. Dabei wird in Zelle 16 die gesamte Duosumme abzüglich der Zahl für Zelle 1 eingesetzt werden. Die Zahl in Zelle 1 sollte mindestens 1 sein.
Das wäre bei einer Summenvorgabe von 472 = 472/2 = 236-1 = 235 für Zelle 16 und 1 für Zelle 1.
Nachfolgend 2 weitere Beispiele zur Berechnung der Duosumme.
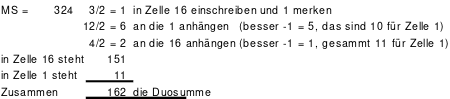
Genau so leicht kann die Duosumme auch für größere Zahlen berechnet werden.
Das Beispiel der weiteren Arbeit erfolgt mit der Vorgabe der magischen Summe von 4765.
Als nächster Schritt ist die Schlüsselzahl zu bestimmen.
Dazu werden die Hunderter der Vorgabe, das ist 47, mit 3 multipliziert und man erhält 47*3 = 141. Mag legt jedoch aus Gründen des leichteren Rechnens und der Sicherheit 109 als Schlüsselzahl fest. Er will damit auch zeigen, dass die Schlüsselzahl nahezu frei gewählt werden kann.
Ganz frei ist nicht möglich. Sie muss kleiner als die berechnete sein, um so Überschneidungen und damit die Gefahr, dass doppelte Zahlen entstehen können, auszuschließen. Zu klein sollte sie auch nicht sein, denn dann entstehen zwischen der aufsteigenden und der absteigenden Reihe auffällige Zahlenlücken.
Warum Mag die Schlüsselzahl durch Multiplikation der Hunderter mit 3 berechnet hat ist leicht zu erklären. Die magische Summe des Topquadrates ist 34 und 34*3 ist 102, d. h. je Hunderter ist die magische Summe 3-mal enthalten. Die 2 von 102 kann vernachlässigt werden, denn die Schlüsselzahl wird mindestens um1 kleiner als der berechnete Wert gewählt.
Nun kann mit der Quadratbildung begonnen werden.
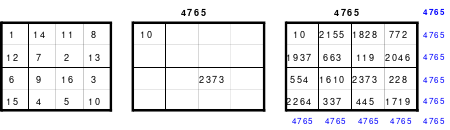
Links das Topquadrat zur Orientierung. Es muss künftig auswendig erlernt sein.
In der Mitte das Startquadrat. Es enthält über dem Quadrat die Vorgabe 4765 und in der Zelle 16 die berechnete Hälfte von 4765 = 2382 mit einem Endrest 1 und weiter
-9 für Zelle 1 = 2373. In die Zelle 1 wird 9 + Endrest 1 = 10 eingesetzt.
Weiter geht es mit den Zellen 2 bis 8 als die aufsteigende Zahlenreihe, die um jeweils 109 erhöht werden. Das ist für Zelle 2 = 10+109=119.
Es wird vereinfacht gerechnet, indem die Hunderter- und Zehnerziffern um 1 erhöht und die Einerziffern um 1 verringert werden.
In Zelle 3 kommt dann 228, in die 4. Zelle 337 usw. bis zur Zelle 8. Aber Achtung in die Zelle 5 kommt nicht 448, sondern 447. Da der Endrest nur einem Block zugeschlagen wird und dieser Block der 1. war, muss die Zelle 5 den Wert 447 erhalten. Anschließend geht es ohne eine Reduzierung weiter. Das ist für Zelle 6 = 447+109=558.
Ist die aufsteigende Zahlenreihe von 1 bis 8 erledigt, geht es an die Abarbeitung der fallenden Zahlenreihe für die Zellen 16 bis 9. Hier werden die folgenden Zellen jeweils um die Schlüsselzahl 109 reduziert. So wird die Zahl für Zelle 15 um 109 kleiner als die Zahl in Zelle 16. Das ist 2373-109 = 2264.
Auch hier wird vereinfacht gerechnet, indem die Hunderter- und Zehnerziffern um jeweils 1 reduziert und die Einerziffern um 1 erhöht werden.
So kommt in die Zelle 14 die Zahl 2264-109 = 2155, in die Zelle 13 die Zahl 2046. So werden alle Zellen bis zur 9. ausgefüllt.
Das rechte Quadrat ist fertig und hat die richtige magische Summe von 4765.
Eine Betrachtung des Ergebnisses
Sie müssen bestätigen, dass die Berechnungen ohne Schwierigkeiten gelöst werden können, besonders, wenn man die von Mag gegebenen Tipps zum vereinfachten rechnen anwendet. Natürlich muss das Topquadrat einwandfrei beherrscht werden.
Doch Mag ist nicht ganz zufrieden mit dem Ergebnis.
Es sind einige Zahlen auffällig. Es sind die Zahlen 119, 228, 337, 445, 554, 663 und 772. Sie sind besonders deshalb auch auffallend, weil sie nacheinander in das Quadrat eingetragen werden. Wer halbwegs rechnen kann, erkennt die einfache Bildung der Zahlen. Das ist das Ergebnis, wenn man es sich zu leicht macht. Die Schlüsselzahl 119 wäre besser gewesen, zumal die berechnete Schlüsselzahl mit 141 das zugelassen hätte. Dann wäre auch nicht die Zahlenlücke zwischen 772 in Zelle 8 und 1610 in Zelle 9 so groß geworden.
Eine noch einfachere Lösung bietet sich an, indem die Duosumme, nicht für die Zelle 1 reduziert wird, sondern vollständig in Zelle 16 kommt. In die Zelle 1 wird ganz einfach nur der Endrest von 1 eingesetzt. Dann wäre das bessere linke Quadrat entstanden.
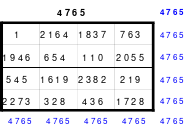
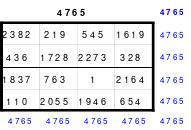
Verbleiben würde jedoch die Eintragung nach der Reihenfolge der Zellenzahlen. Hier kann erkannte werden, dass die Eintragungen gleichmäßig ansteigen, bzw. sich
vermindern. Das kann auch noch vermieden werden, wenn man die Eintragungen, beginnend mit der Duosumme in die Zelle oben links, zeilenweise vornimmt, wobei die Rechenleistungen etwas ansteigen. Das rechte Quadrat wurde in dieser Weise gestaltet. Hierzu erfolgen weitere Erläuterungen in der “Hohen Schule” des Hexen 1x1.
Eine Berechnung der magischen Summe durch Multiplikation der Duosumme mit 2 wird nur ganz selten notwendig werden. Mag geht später in den Beispielen, wo es erforderlich wird, näher darauf ein.
Zum Pentaquadrat
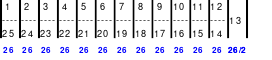
Da das Pentaquadrat ein Quadrat mit ungerader Ordnungszahl ist, gibt es kein mittleres Duo, sondern eine Zahl, die der Hälfte der Duosumme, das ist 26/2 = 13 entspricht. Das ist 1/5 der magischen Summe des Pentaquadrates von 65. Umgekehrt ist das 5-fache der Zahl 13 gleich die magische Summe von 65.
Alle Duos haben die einheitliche Summe von 26. Das ist das 5/2-fache der magischen Summe des Pentaquadrates von 65
Schlussfolgerung: Die Zahl in Zelle 13 ist ein Fünftel der magischen Summe bzw. die magische Summe ist das Fünffache der Zahl in Zelle 13.Allgemeingültig für pandiagonale Primquadrate heiß das, die Zahl für die mittlere Zelle ergibt sich aus der Division der magischen Summe durch die Ordnungszahl und umgekehrt erhält man die magische Summe durch Multiplikation der Zahl in der mittleren Zelle mit der Ordnungszahl.
Die mittlere Zelle errechnet sich aus (O2 + 1) /2. Daraus ergeben sich für die Arbeit mit dem Pentaquadrat andere Wege der Berechnungen als beim Topquadrat.
Das linke Pentaquadrat wurde durch Versetzen der untersten Zeile nach oben zum rechten Quadrat verändert. Die 13 als mittlere Zahl befindet sich jetzt in der 1. Zelle der Zeile 1. Sie ist die so genannte Startzelle, in die in der Regel die 1. Zahl eingesetzt wird
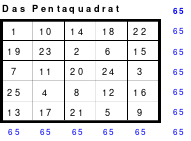
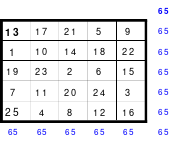
Von Bedeutung ist, dass unter der Zelle 13 die Zelle 1, die kleinste, zu finden ist und die Zelle 25, die größte, befindet sich als 1. in der untersten Zeile. Dies 3 Zellen sind hervorgehoben dargestellt.
Vorgabe der magischen Summe
Es soll ein magisches Quadrat mit der vorgegebenen magischen Summe von 827 gebildet werden.
1. Schritt:
Berechnung der Zahl für Zelle 13. Diese ergibt sich aus 827/5=165, Rest 2
(Im Einzelnen: 8/5=1, einschreiben, 32/5=6, anhängen, 27/5=5, anhängen und in Zelle 13 steht 165.) Den Rest 2 merken oder in die Zelle 1 einsetzen.
2. Schritt:
Festlegung der Schlüsselzahl. Von der 165 in Zelle 13 muss 12-mal die Schlüsselzahl abgezogen werden um die Zahl für Zelle 1 zu erhalten. Diese darf nicht kleiner 1 werden. Da 100/12~8 ist, wird 1,6*8=12,8 gerechnet und die kleinere Zahl 9 als Schlüsselzahl gewählt.
3. Schritt:
Berechnung der Zahlen für den mittleren Block. Siehe dazu rechtes Quadrat. Der mittlere Block enthält die Zahlen von 11 bis 15. Von Zelle 13 aus heißt das, es müssen 2 Zahlen rückwärts und 2 Zahlen vorwärts berechnet werden. Als 1. die Rückwärtsberechnung. Von Zelle 13 aus 1 nach oben und 2 nach links und dort 165-9=156 einsetzen. Von dort wieder 1 nach oben und 2 nach links und dort 156-9=147 einsetzen.
Nun die Vorwärtsberechnung Von Zelle 13 aus 2 nach rechts und 1 nach unten und die Zahl 165+9=174 eintragen. Weiter 2 nach rechts und 1 nach unten und dort 174+9=183 einsetzen. Fertig.
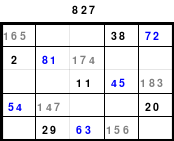
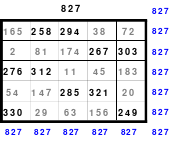
4. Schritt:
Berechnung der aufsteigenden Zahlen, begonnen in Zelle 1. (Siehe dazu Quadrat links, in dem alle bereits berechneten Zahlen zurückhaltend grau gehalten sind.)
In die Zelle 1 wird, wenn noch nicht erfolgt, der Rest 2 eingesetzt.
Von dort werden die um jeweils 9 erhöhten Zahlen eingegeben. Das ist 2 nach rechts und 1 nach unten 165+9=174. So geht es weiter bis zur 38 in Zelle 5. 2 nach rechts und 1 nach unten geht nicht, da dort die Zelle 1 mit der Zahl 2 belegt ist. Das bedeutet, dass der 1. Block fertig ist und zum 2. übergegangen werden muss. Das sind 2 Zellen nach unten.
Aber Achtung! Der Rest darf nur einem Block zugeschlagen werden. Folglich kommt in die Zelle 6 die Zahl 38-2+9=45. Dann weiter wie vorher bis zur 81 in Zelle 10. Von dort kann weder zur nächsten Zelle gesprungen, aber auch nicht mit 2 nach unten zum nächsten Block übergegangen werden. Denn diese Zellen sind bereits mit Zahlen belegt. Damit wird signalisiert, dass die Blöcke 1 und 2 fertig sind. Jetzt verstehen Sie auch, weshalb als erstes der mittlere Block berechnet wurde.
5. Schritt:
(Siehe Quadrat rechts.) Ausgehend von Zelle 25 werden die Zellen der Blöcke 4 und 5 absteigend mit Zahlen ausgefüllt. Dazu muss die Zahl für Zelle 25 ermittelt werden. Die Zellen 1 und 25 bilden ein Duo mit der 2-fachen Summe der Zahl in Zelle 13. Da in der Zelle 1 nach Abzug des Restes der Wert 0 steht, kommt in die Zelle 25 die gesamte Duosumme. Das ist 165*2=330. Von dort 1 nach oben und 2 nach links zur Zelle 24 in die 330-9=321 kommt. So werden alle anderen Zahlen eingesetzt bis zur Zelle 16, der letzten Zelle ganz unten rechts, in der die Zahl 249 kommt. Von dort kann es ebenfalls nicht mehr weiter gehen, da die in Frage kommenden Zellen belegt sind. Es ist auch keine Zelle mehr ohne Zahl.
Eine Nachbetrachtung
Sicherlich stellen Sie die Frage, was in die Zelle 1 eingesetzt werden soll, wenn kein Rest entsteht?
Es kann eine beliebige Zahl eingesetzt werden. Es muss nur beachtet werden, dass die Zahl von der Duosumme abgezogen werden muss und die für die Zelle 25 verbleibende Zahl noch groß genug ist, um von dieser 12 mal die Schlüsselzahl abziehen zu können ohne dabei zu einer kleineren Zahl als die Zahl in Zelle 13 zu kommen. Denn sonst besteht die Gefahr das doppelte Zahlen entstehen können.
Das klingt zwar kompliziert wird aber ganz einfach gesichert, indem von der Zahl in Zelle 13 das 12-fache der Schlüsselzahl abgezogen wird. Dabei kann ganz grob gerechnet werden. Im Beispiel 165-12*10=45. (Die 10 steht für die Schlüsselzahl 9).
Im Ergebnis darf die Zahl für Zelle 1 bis 45 groß sein.
Würde z. B. 37 in die Zelle 1 eingesetzt werden, so verbleibt für die Zelle 25 die Differenz zur Duosumme von 330-37=293.
(Natürlich ist das mit der Vorgabe der magischen Summe von 825 möglich.)
Die Zahl für Zelle 1 kann auch bei einem Rest verändert werden. In diesem Fall wird die gewählte Zahl um den Rest erhöht. Im berechneten Beispiel mit der magischen Summe von 827 würde dann die Zahl für die 1. Zelle 37+2=39 sein.
Wenn kein Rest anfällt, so kann die Berechnung des Quadrates auch in einer anderen Form erfolgen und zwar analog der nächsten Abhandlung zur Vorgabe einer Zahl für eine Zelle.
Vorgabe einer Zahl für eine Zelle
Mag bittet um eine 3-stellige Zahl. Es wird 347 genannt die er in die Zelle 13 einschreibt. Anschließend schreibt er über das Quadrat die Zahl 1735 und setzt in die Zellen in scheinbar ungeordnetem System Zahlen ein. Das fertige Quadrat ist magisch mit der magischen Summe von 1735.
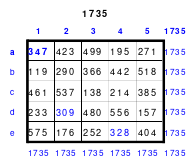
Lösung
Zum besseren Verständnis hat Mag die Spalten und Zeilen mit Zahlen und Buchstaben versehen. Diese haben im Original natürlich nichts zu suchen.
Da die magische Summe das 5-fache der Zahl aus Zelle 13 ist, hat Mag 347*5=1735 gerechnet und über das Quadrat geschrieben. Selbstverständlich hat Mag einfacher gerechnet. Da 10/2 auch 5 ist, hat er die 347 gedanklich durch Anhängen einer 0 verzehnfacht und dann durch 2 geteilt. Durch diesen Trick kann die magische Summe einfach berechnet und von links nach rechts geschrieben werden.
Die Schlüsselzahl hat Mag mit 3*8=24, gewählt 19 festgelegt.
Aus Sicherheitsgründen wurden, wie bei der Summenvorgabe, als erstes die Zahlen für die Zellen 12 (4e) und 11 (2d) absteigend mit 328 und 309 ermittelt.
Danach wurden ausgehend von Zelle 13 aufsteigend die Zahlen für die Zellen 14 bis 25 wie bekannt berechnet. Mit der Zahl 575 in Zelle 25 (1e) ist die aufsteigende Reihe abgeschlossen.
Es folgt die absteigende Reihe, die nicht mit Zelle 13 begonnen wird, sondern mit der bereits berechneten Zahl in Zelle 11 (2d). Da diese die 1. Zahl im 3. Block ist, muss rückwärts zur Zelle 10, die 5. Zahl im Block 2 gegangen werden, Das ist 2 Zellen nach oben zur Zelle 10 (2b) in die die Zahl 290 kommt. Dann weiter wie bekannt.
Und wenn Mag alles richtig gemacht haben, so endet er in der Zelle 1 (1b) mit der Zahl 119 und die magische Summe ist wie vorausberechnet 1735 (hoffentlich!).
Vorgabe einer Zelle
Um die Berechnungen (scheinbar) noch weiter zu steigern, kann um die Nennung der Zelle, mit der begonnen werden soll, gebeten werden.
Egal welche Zelle gewählt wird, für den Akteur ist es die Zelle 13 und darüber ist die Zelle 25 und darunter die Zelle 1. Das ist möglich, da das Pentaquadrat ein 100%ig homogenes Quadrat ist, bei dem Zeilen und/oder Spalten versetz werden können.
Dabei brauchen Sie sich keine Gedanken über die veränderte Struktur des Quadrates zu machen, denn alle Berechnungen beginnen und enden in den Zellen 13, 1 und 25.
6.2. Quadrate der 3. Ordnung
6.2.1. Analyse des Lo-Shu-Quadrates (Das Unveränderliche)
Allgemeines
Das Lo Shu-Quadrat ist das kleinstmögliche magische Quadrat. Mag nennt es deshalb auch das Miniquadrat. Es ist das älteste bekannte Quadrat, denn es wurde bereits 1200 v. Chr. dokumentiert (diese Jahreszahl wird nicht einheitlich genannt). Danach soll eine Schildkröte dem Fluss Lo entstiegen sein, auf deren Rücken das Lo-Shu-Quadrat, ein 3-mal 3 = 9 Zahlen großes Quadrat, abgebildet war.
Im Internet sind viele Beiträge zum Lo-Shu-Quadrat zu finden, die sich in vielfältiger Form, mathematisch, religiös, astrologisch und weiteren, mit diesem Quadrat beschäftigen.
Mag hat aber keine Beiträge über die Ableitung zu größeren magischen Quadraten und deren Einsatz in der Rechenkunst gefunden.
(Wahrscheinlich hat er nicht lange genug recherchiert?)
Mag wird nachfolgend einige Betrachtungen zum Lo Shu- Quadrat vornehmen, wobei er nur auf die Eigenschaften und Probleme eingeht, die für seine weiteren Darlegungen von Bedeutung sind. Dabei wird er sich nur auf Ergebnisse seiner Analyse beschränken und auf eine weitgehende mathematische Beweisführung verzichten.
Diese Darlegungen werden zum Teil in den weiteren Beiträgen als Grundlage wiederholt.
Das Unveränderliche
Das Miniquadrat ist in seiner Grundstruktur unveränderlich. Es können weder Zeilen oder Spalten versetzt werden. Auch eine veränderte Zahleneintragung ist unmöglich. Die einzig mögliche Veränderung ist das Drehen und Wenden des Quadrates, wobei es seine Grundstruktur logischerweise nicht verändert.
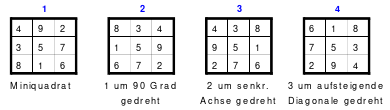
Mathematische Regeln
1. Das Quadrat ist magisch, die magische Summe des Basisquadrates beträgt 15.
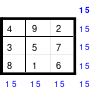
2. Das Quadrat bleibt magisch, wenn alle Zellen gleichbehandelt werden:
Die Differenzen zwischen den Zahlen der 3 Blöcke müssen einheitlich sein. Das wird durch die Gleichbehandlung gesichert, wie es die folgenden Quadrate beweisen.
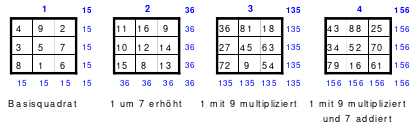
3. Das Quadrat bleibt magisch, wenn die Differenz zwischen den Blöcken gleiche Größe haben, wobei diese Größe nicht der Differenz zwischen den Zahlen der Blöcke entsprechen muss.
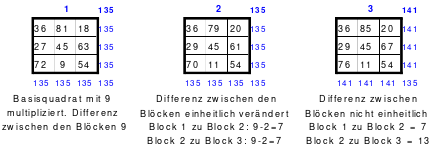
Das 2. Quadrat ist mit gleicher Summe magisch geblieben, Lediglich die Zahlen des 1. und 3. Blockes haben sich verändert.
Das Quadrat 3 ist nicht mehr magisch, da die fallende Diagonale nicht die magische Summe hat.
4. Die magische Summe muss durch 3 teilbar sein. Der Grund dafür ist, dass die mittlere Zahl 5 das 3-fache der magischen Summe ist und durch Division der magischen Summe durch 3 ermittelt wird. Ist die Vorgabe nicht durch 3 teilbar verbleibt ein Rest der nicht so eingeordnet werden kann, dass er in jeder Reihe nur 1-mal wirksam wird.
Um die Teilbarkeit durch 3 zu sichern, sind neben der bereits erläuterten Würfelvariante weitere Manipulationen möglich:
Eine sehr bekannte Möglichkeit ist die Bitte um eine Zahl, von der die Quersumme abgezogen werden soll. Das Ergebnis ist durch 9 und damit auch durch 3 teilbar.
Beispiel: frei gewählte Zahl = 539 - 17 = 522; 522 / 3 = 174
Es wird um eine Zahl aus unterschiedlichen Ziffern gebeten. Anschließend soll diese Zahl in umgekehrter Reihenfolge notiert werden. Die zu bildende Differenz zwischen den beiden Zahlen ist ebenfalls durch 9 teilbar.
Beispiel: 834 - 438 = 396 oder 716 - 617 = 99
Diese Beispiele offenbaren das Problem, dass das Ergebnis sehr unterschiedlich ausfällt, was evtl. nicht gewünscht wird.
Man lässt sich eine kleine Zahl vorgeben als die, mit der man arbeiten möchte. Mit den Worten: “Ich bin heute in guter Form und wage es mit einer größeren Zahl. Ich erlaube mir diese zu vergrößern.” (Oder so ähnlich) Mit diesen Worten hängt er eine Ziffer an die vorgegebene Zahl. Diese Ziffer wird so gewählt, dass die Quersumme der Vorgabe durch 3 geteilt werden kann. Beispiel: Man will mit einer 4-stelligen Zahl arbeiten, bittet aber um Nennung einer 3-stelligen. Es wird 487 genannt. Die Quersumme ist 19. Die nächste durch 3 teilbare Zahl wäre die 21. Es wird folglich die Vorgabe durch Anhängen einer 2 auf eine 4-stellige, durch 3 teilbare Zahl erweitert. Auch eine 5 oder 8 kann angehängt werden.
Die Vorzugsvariante lässt eine begrenzte Steuerung der Vorgabengröße zu. Aus einer Ziffernreihe von 1 bis n ist durch Addition von mehrstelligen frei gebildeten Zahlen eine Summe zu bilden. Dabei darf jede Ziffer nur einmal eingesetzt werden.
Folgende Beispiele sind möglich:
Ziffernfolge: 1 2 3 4 5 6 Es sollen aus den Ziffern 2-stellige Zahlen gebildet und addiert werden, dabei darf jede Ziffer nur einmal eingesetzt werden.
Das könnte sein: 25 + 63 + 41 = 129 ist durch 3 teilbar
bei 3-stelligen Zahlen: 634 + 521 = 1155 ist durch 3 teilbar
oder 1-, 2- und 3-stellige: 41 + 532 + 6 = 579 ist durch 3 teilbar
Im letzten Fall könnte die Berechnung nach Bildung der ersten 2 Zahlen abgebrochen werden. Da nur die 6, eine durch 3 teilbare Zahl übrig ist, ist die Summe der 2 Zahlen bereits durch 3 teilbar: 41 + 532 = 573.
Die unterschiedlichen Ergebnisse in den Beispielen zeigen, dass durch Vorgabe der Größe der zu bildenden Zahlen eine gegrenzte Steuerung möglich ist.
Andere Zifferfolgen können sein: 1 2 3 4 5 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9
Die Quersummen dieser Ziffernfolgen sind durch 3 teilbar und damit auch die gebildeten Zahlen, egal wie diese zusammengesetzt werden. Auch die Multiplikation ist möglich.
6.2.2. Das kleine Hexen 1x1 mit dem Miniquadrat
Die Berechnung magischer Quadrate auf der Grundlage vorgegebener Zahlen ist ebenfalls Bestandteil der Rechenkunst.
Mag wird Rechenexperimente mit einem Quadrat der 3. Ordnung darstellen. Das Quadrat der 3. Ordnung ist das kleinstmögliche magische Quadrat, weshalb Mag es als Miniquadrat bezeichnet.
Die Beispiele erfolgen unter Einsatz von nur 2-stelligen Zahlen. Die Bildung größerer Quadrate auch mit größeren Zahlen finden Sie im Anschluss.
Zum besseren Verständnis sind jedoch ein paar Erläuterungen zum Miniquadrat (Abb. 1) notwendig.
Die Zahlen von 1 bis 9 werden in 3 Blöcke unterteilt. Block 1 enthält die Zahlen 1, 2 und 3. Der Block 2 die Zahlen 4, 5, 6 und der Block 3 die Zahlen 7, 8 und 9.
Analysiert man die Einordnung der Zahlen, so findet man in jeder Zeile, Spalte und der aufsteigenden Diagonalen je eine Zahl aus den 3 Blöcken. Auf die fallende Diagonale mit den Zahlen 4, 5 und 6 trifft das nicht zu. Daraus ergeben sich bestimmte Bedingungen bei der Bildung eines Miniquadrates. Diese sind:
Die Differenzen zwischen den Zahlen müssen gleich groß sein. (Abb. 2)
Die Differenzen zwischen den einzelnen Blöcken müssen ebenfalls gleiche Größe haben. (Abb. 3)
Eine Veränderung der Zahlen durch Addition und/oder Multiplikation muss für alle Zellenzahlen gleich sein. (Abb. 4)
Die magische Summe des Miniquadrates muss immer durch 3 teilbar sein.
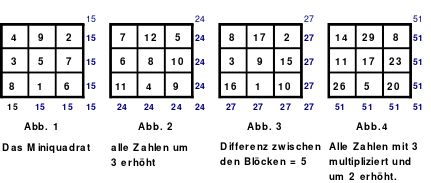
Eine Veränderung der Zahlen durch Addition und/oder Multiplikation kann auch mit den Quadraten nach Abb. 2 und 3 erfolgen. Dies wird aber nicht weiter berücksichtigt, da es bei den nachfolgenden Ausführungen nicht zur Anwendung kommt. Es wird immer das Miniquadrat als Vorlage für die Berechnungen genutzt.
Doch nun zu den Vorführungen von Mag.
Summenvorgabe
Mag hat auf die Tafel ein Miniquadrat ohne Zahlen gezeichnet.
Er bittet einen Zuschauer eine größere 2-stellige Zahl zu nennen. Der Zuschauer wählt die Zahl 72. Diese Zahl schreibt Mag über das Quadrat.
Mag beginnt sofort mit der Eintragung von Zahlen in das Miniquadrat.
Dabei werden nacheinander Diagonalen, Zeilen und Spalten fertig gestellt. Die Jury und auch die Zuschauer können sich überzeugen, dass die Summen der Reihen der vorgegebenen magischen Summe entsprechen.
Nach dem er in alle Zellen eine Zahl eingeschrieben hat, weist er darauf hin, dass alle Zeilen, Spalten und die Diagonalen die einheitliche Summe von 72, wie vorgegeben haben und dass damit das Quadrat ein magisches ist, bei dem keine Zahl doppelt vorkommt.
Lösung
Mag hat aus der Quersumme 7 + 2 = 9 erkannt, dass die Zahl 72 durch 3 teilbar ist und folglich als magische Summe für das Miniquadrat infrage kommen kann. Die Zahlenfolge im Miniquadrat beherrscht er auswendig. Er weiß auch, dass die Zahl für Zelle 5 ein Drittel der magischen Summe von 15, dem Basisquadrat entspricht. Das ist auch magische Summe dividiert durch die Ordnungszahl.
Als Erstes dividiert Mag die Vorgabe 72 durch die Ordnungszahl des Basisquadrates von 3 und erhält so die halbe Duogröße von 72/3 = 24 für die Zelle 5. Die 24 könnte schon in die Zelle 5 eingetragen werden. Besser ist es, man ermittelt erstmal die Schlüsselzahl um die alle anderen Zellenzahlen erhöht, bzw. vermindert werden müssen um gleiche Zahlen zu vermeiden. Theoretisch wäre es möglich die 24 in alle Zellen einzusetzen. Die Summen aller Reihen würden dann 72 betragen. Das kann natürlich nicht so erfolgen! Von der Zahl in Zelle 5 müsste 4-mal eine Zahl abgezogen werden, um die Zahl für Zelle 1 zu erhalten. Da diese nicht Null sein soll geht man auf Sicherheit und dividiert die Zahl für Zelle 5 durch 5 und erhält in diesem Fall die gekürzte Zahl 24/5=4. Da 4 nicht gerade geeignet ist, denn so würden nur gerade Zahlen im Quadrat zustande kommen, wird eine geeignetere Schlüsselzahl gewählt, die lediglich kleiner sein muss. Anderenfalls kann es zu unzulässigen negativen Zahlen kommen. Im Beispiel bietet sich die 3 als Schlüsselzahl an.
Nun kann zügig mit der Eintragung der Zahlen in die Zellen begonnen werden. Zuerst kommt in die Zelle 4 (links/oben) die Zahl 24 - 3 = 21. Dann zur Zelle 5, in die die 24 kommt. Weiter zur Zelle 6 (rechts/unten) in die 24 + 3 = 27 eingesetzt wird, denn 6 ist um 1 größer als 5. Damit ist die fallende Diagonale fertig und kann zur Kontrolle angeboten werden.
Weiter geht es von der Zelle 6 zur Zelle 7, das ist 1 nach oben und hier wird die Zahl aus Zelle 6 um 1-mal 3 erhöht, das ist 27 + 3 = 30. In die Zelle 3 wird die Zahl aus Zelle 4 um 3 auf 18 reduziert und die 1. Zeile ist ebenfalls fertig. So geht es weiter zur Zelle 2, wo die Zahl aus Zelle 3 - 3, das ist 18 - 3 = 15 eingeschrieben wird. usw. usw. bis alle Zellen mit Zahlen ausgefüllt sind.
Das fertige Ergebnis entspricht der Abbildung.
Scheinbar haben Sie sich bemüht, eine Reihe nach der anderen mit Zahlen zu belegen. In Wirklichkeit haben Sie den leichtesten Rechenweg mit jeweils +/- 3 gewählt.
Sicherlich fragen Sie sich was zu tun ist, wenn der Zuschauer eine nicht durch 3 teilbare Zahl, zum Beispiel 62, vorgibt? Immerhin trifft das ja im Mittel auf 2 von 3 Zahlen zu!
Übrigens hat Mag ja nicht gesagt, was mit der Vorgabe geschehen soll. Sie muss ja nicht als Summenvorgabe betrachtet werden. Sie kann genauso gut eine Vorgabe einer Zellenzahl sein und Mag weicht ganz einfach auf eine Zahlenvorgabe aus.
Zahlenvorgabe
Mag lässt sich eine beliebige 2-stellige Zahl nennen. Bleiben wir bei der 62, die als magische Summe nicht in Frage kommt.
Die 62 wird in die Zelle 4 (oben/links) eingesetzt. Sofort wird die magische Summe von 225 über das Quadrat geschrieben.
Anschließend werden in alle Zellen, wie bei der Summenvorgabe, Zahlen eingesetzt. Das fertige Quadrat ist das folgende. Es ist magisch mit der magischen Summe von 225. Alle Zahlen kommen nur einmal vor.
Lösung
Die 62 wurde in die Zelle 4 eingesetzt. Daraus wird die Schlüsselzahl mit 62/4=15, gewählt 13 errechnet.
Die Zahl für Zelle 5 ist folglich 62+13=75. Diese wird aber nicht sofort in die Zelle 5 eingesetzt, sondern wird mit 3 multipliziert, das ist 75*3=225 und als magische Summe über das Quadrat geschrieben.
Jetzt kann die 75 in die Zelle 5 eingetragen werden. Anschließend 75+13=88 für Zelle 6. Alles Weitere läuft wie bei der Summenvorgabe ab und bedarf keiner weiteren Erläuterungen.
Hinweise
Die Summenvorgabe sollte größer 70, besser größer 90 sein, weil dann die Schlüsselzahl 7 bzw. 9 groß ist und damit eine gute Zahlenbildung ermöglicht. Eine Schlüsselzahl von 3 ist möglich, aber leicht zu durchschauen. Am besten ist es, man lässt sich eine 3-stelige Summe als magische Summe vorgeben bzw. nach den Vorschlägen bilden. Das Rechnen mit einer eventuell sehr großen Vorgabe ist nicht viel schwerer und wird in den weiteren Darlegungen beschrieben.
Etwas komplizierter ist die Vorgabe einer sehr kleinen 2-stelligen Zahlenvorgabe, wie z. B. 13. Wird diese in die Zelle 4 eingegeben, so kann die Schlüsselzahl nicht größer 3 gewählt werden. In diesem Falle bieten sich eine Möglichkeit zur Bildung einer größeren Schlüsselzahl an. Man setzt die Vorgabe ganz einfach in die Zelle 1 oder 2 ein. Die Schlüsselzahl kann dann mit 9 festgelegt werden. Die Zahl für Zelle 5 wird dann durch Addition von 3 (bei Zelle 2) bzw. 4-mal die Schlüsselzahl (bei Zelle 1) berechnet.
6.2.3. Hohe Schule des Hexen 1x1
Bei der “Hohen Schule” geht es um die Quadratbildung mit größeren Vorgaben, Mehrfach-Vorgaben und eine zeilenweise Eintragung der Zahlen in die Zellen.
Diese Aufgaben sind im Miniquadrat oft schwerer zu lösen als im Topquadrat. Mag verzichtet deshalb auf umfassende Darlegungen von Beispielen. Nach Auswertung der Beschreibungen zum Topquadrat können diese teilweise auch im Miniquadrat angewendet werden.
Mag beschreibt jetzt ein Beispiel, in dem alle Möglichkeiten vereint zum Einsatz kommen. Es geht um eine Quadratbildung bei Vorgabe der magischen Summe, einer Zellenzahl und die Bestimmung in welche Zelle diese eingesetzt werden soll und die zeilenweise Fertigstellung des Quadrates.
Diese Aufgabe ist nicht so leicht zu lösen wie die Experimente im kleinen Hexen 1x1, was nicht nur für Anfänger der Fall sein dürfte. Mag hat deswegen dieser Aufgabe einen Stern zugesprochen.
Es sollen 3 Vorgaben gemacht werden.
Summenvorgabe
Auf einer Tafel hat Mag ein leeres Quadrat der 3. Ordnung aufgezeichnet. Darüber die Ziffern von 1 bis 9. Er bittet mehrere Zuschauer daraus nach freier Wahl 1-, 2- oder 3-stellige Zahlen zu bilden und diese untereinander zu schreiben. Jede Ziffer darf nur einmal eingesetzt werden. Im Beispiel sind es die Zahlen 592, 86 und 741. Von den Ziffern ist nur noch die 3 übrig, die nicht mehr berücksichtigt werden muss. Da 3 eine durch 3 dividierbare Zahl ist, ist die bisher gebildete Zahl bereits durch 3 teilbar.
Mag bittet nun diese Zahlen zu addieren und das Ergebnis unter die Zahlen zu schreiben. Im Beispiel ist das 1416.
Um Fehler zu vermeiden ist es besser, sich von mehreren Zuschauern die Zahlen nennen zu lassen, diese selbst aufzuschreiben und zu addieren.
1 2 3 4 5 6 7 8 9
Zahlenvorgabe
Als nächstes bittet Mag einen weiteren Gast um die Nennung einer 3-steligen Zahl, Dieser nennt die Zahl 271.
Zellenvorgabe
Ein weiterer Gast wird gebeten eine äußere Zelle zu nennen, in die diese Zahl eingesetzt werden soll. Es wird die 3. Zelle in der 2 Reihe genannt. In diese schreibt Mag die Vorgabe 271.
Damit sind alle Vorgaben unter Einbeziehung mehrere Zuschauer gemacht und die Quadratbildung kann vorgenommen werden.
Bemerkungen zu den Vorgaben
Zuvor jedoch noch einige Bemerkungen zu den Vorgaben.
Die Summenvorgabe muss meist etwas gesteuert werden.
Um ein leichtes Rechnen zu ermöglichen, wird von Anfang an die Zahl 109 als Schlüsselzahl gewählt. Das ist auch +109=+110-1 und -109=-110+1. Daraus ergibt sich eine erforderliche magische Summe von mindestens 1311. Die Summenvorgabe 1419 erfüllt diese Forderung gerade noch. Man sollte eine Mindestsumme von ~ 1500 zur Orientierung wählen. Werden aus den 9 Ziffern 3-stellige Zahlen gebildet, so ist als kleinste Summe 774 und als größte 2556 möglich. Es sollte deshalb um Nennung 3-stelliger Zahlen gebeten werden. Ist die 1. Zahl sehr klein, so bittet man als nächstes um eine 4-stellige Zahl, die natürlich auch sehr groß ausfallen kann, was aber nicht ungünstig ist. Denn die Zahlenvorgabe sollte bei einer kleinen Summenvorgabe nicht größer als ~800 sein. Anderenfalls kann die Schlüsselzahl 109 nicht zur Anwendung kommen bzw. es würden negative Zahlen entstehen. Sie soll größer 109 sein, was in der Regel zutrifft. Im Ausnahmefall bittet man den Gast nicht zu zaghaft zu sein und eine größere Zahl zu nennen.
Da die genannten Parameter eingehalten sind, kann mit der Quadratbildung begonnen werden.
Die Quadratbildung
Als erstes muss die Zelle, in der die Zahl 271 steht, bestimmt werden. Denn die Zelle 7 kommt nicht in Betracht, da von 271 nicht 7 mal 109 abgezogen werden kann. (genauer 6 mal 109, wobei ein Rest für Zelle 1 von mindestens 1 verbleiben muss.)
Von der Zahl 271 kann lediglich 2 mal 109 (einfacher 2 mal 110) abgezogen werden.
Folglich kommen nur die Zellen 1 und 3 in Frage. Die Zelle 2 scheidet aus, da sie eine Eckzelle ist. Günstig ist Zelle 3, da das Miniquadrat nur um die senkrechte Achse gedreht werden muss und die gewählte Zelle ist die Zelle 3.
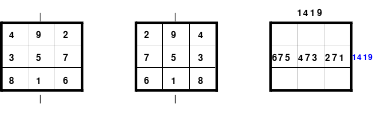
In die Zelle 5 wird 1419/3=473 eingeschrieben.
Die nächste Rechenoperation ist die schwierigste.
In jeder Reihe des Basisquadrates bilden die beiden Zahlen außer der 5 als Summe 10, das ist das Doppelte von 5, oder auch die magische Summe von 15-5=10.
Die Zahl für die Zelle 7 muss berechnet werden, indem die Zahl in Zelle 5 verdoppelt werden muss und anschließend von dieser Summe die Zahl aus Zelle 3, die 271, abgezogen wird. Das ist 473*2=946 und weiter 946-271=675, die in Zelle 7 kommt. Damit ist die erste Zeile fertig und die Jury kann sich überzeugen, dass die Summe der 3 Zahlen mit 1419, der Vorgabe entspricht.
Gleichzeitig sind die Voraussetzungen geschaffen, um alle weiteren Zellenzahlen zu berechnen. Denn die 3 Zahlen sind je eine aus einem der 3 Blöcke. Die 271 ist die 3. Zahl im 1. Block, die 473 ist die 2. Zahl im 2. Block und die 675 ist die 1. Zahl im 3. Block.
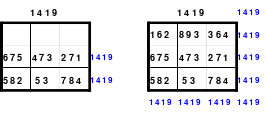
Die nächste Zeile ist die unterste mit der linken Zelle 6, das ist um 1 größer als 5. Folglich wird die neue Zellenzahl in Zelle 6 = 473+1*109=582.
(Dabei wird rationell gerechnet, indem die 4 und 7 um je 1 erhöht und die letzte Ziffer 3 um 1 reduziert wird.)
Weiter, in Zelle 1 kommt 271-2*109=53 und in Zelle 8 kommt 675+1*109=784.
Auch diese Zeile hat als magische Summe die vorgegebenen 1419.
Wichtig ist, dass immer Bezug zu einer vorhandenen Zellenzahl des gleichen Blockes genommen wird. Maximal wird das 2-fache von 109 zu- oder abgerechnet.
Die 1. Zeile des Quadrates ist wie die 3. leicht zu berechnen. Links ist die Zelle 2, die um 1*109 größer als die Zahl in Zelle 1 ist. Das ist 53+1*109=162. Dann folgen Zelle 9 mit 784+1*109=893 und die letzte Zahl 473-1*109=364.
(Keinesfalls Zahl aus Zelle 3+1*109=380, das ist falsch und kommt raus, wenn man nicht innerhalb der Blöcke bleibt.)
Das magische Quadrat der 3. Ordnung mit der magischen Summe von 1419 ist fertig!
Mag weist zum Abschluss darauf hin, dass das Quadrat ein magisches ist und keine Zahl doppelt vorkommt.
Eine Nachbetrachtung
Mag erachtet eine nähere Betrachtung der Bestimmung der richtigen Zelle für die Zahlenvorgabe als sinnvoll. Es kann nicht nur für einen Anfänger eventuell schwierig sein, sich mit gedrehten und gewendeten Miniquadraten zurechtzufinden.
Im Allgemeinen reicht die Vorstellungskraft aus, um ein um die waagerechte oder senkrechte Achse gewendetes Quadrat zu beherrschen. Schwieriger wird es, wenn es um die Diagonalen gewendet werden muss. Das ist der z. B. Fall, wenn die Zelle 3 zur Zelle 1 werden soll.
In diesen Fällen sollte vorerst auf die Bestimmung der Zelle für die Vorgabe durch einen Zuschauer verzichtet werden und die Zahl direkt in die richtige Zelle geschrieben werden.
Wenn auf die Vorgabe der Zelle nicht verzichtet werden soll, ist zu beachten:
Die Zellenzahl, bezogen auf das Basisquadrat, darf jedoch nicht größer sein als sich aus Vorgabe dividiert durch 110 ergibt. Anderenfalls kommt es zu negativen Zahlen. Im vorliegenden Fall kämen nur die Zellen 1, 2 und 3 in Frage, wovon die 2 ausscheidet, da diese eine Eckzelle ist. Um aus der Zelle 7 die Zelle 1 zu machen wäre das Wenden des Quadrates um die fallende Diagonale Achse notwendig. Einfacher ist das Wenden um die senkrechte Achse, was Mag auch machte.
Zurück zur Zellenbestimmung.
Miniquadrat um 90o nach um 180o nach um 90o nach
rechts gedreht rechts gedreht links gedreht
Eine vielleicht bessere Variante ist das Drehen des Quadrates um den Mittelpunkt, wie es in den obigen Abbildungen gezeigt wird. Hier können alle geraden Eckzellen und die ungeraden Zellen in der Mitte der Reihen die Plätze ändern.
Im rechten Quadrat werden die Variationsmöglichkeiten aufgezeigt.
Wird die Zahl in eine rote Zelle eingeschrieben, so kann diese als Zelle 1; 3; 7; oder 9 gewertet werden. Erfolgt der Eintrag in eine grüne Zelle, so kann diese als Zelle 2; 4; 6 oder 8 bestimmt werden. Lediglich die mittlere Zelle 5 ist unveränderlich und darf nicht zur Wahl angeboten werden. Sie ist einzig und allein für Sie bestimmt.
6.3. Quadrate der 4. Ordnung
6.3.1. Das Topquadrat
Die Duos
Das Topquadrat ist das am meisten in Vorführungen eingesetzte Quadrat. Es ist das kleinste pandiagonale und zumindest teilhomogene Quadrat. Die 16 Zahlen und deren Einordnung in das Quadrat ist ziemlich leicht erlernbar.
Die Zahlen des Topquadrates können als Duoreihe dargestellt werden.
Da das Topquadrat ein Quadrat mit gerader Ordnungszahl ist, gibt es keine mittlere Zahl. Die Mitte wird durch das Duopaar 8/9 gebildet.
Alle Duos haben die einheitliche Summe von 17. Das ist die Hälfte der magischen Summe des Topquadrates von 34. Jedes Duo belegt 2 Zellen und das ist die Hälfte der 4 Zellen je Reihe im Topquadrat.
Schlussfolgerung: Die Summe jedes Duopaares entspricht der halben magischen Summe des Topquadrates und umgekehrt ergibt die Verdopplung eines Duopaares die magische Summe.
Interessant ist auch die Einordnung der Duos in das Topquadrat. Die 2 Zahlen jedes Duopaares sind im Abstand von 2 Zellen in diagonaler Richtung innerhalb des Quadrates eingeordnet. Dabei ist es egal in welcher Richtung die Paare zueinander eingeordnet sind. Das ist anhand der Duopaare 1/16 und 2/15 in den unten gezeigten Quadraten zu erkennen. Das rechte Quadrat wurde durch Versetzen der 2 oberen Zeilen nach unten und der 1. Spalte nach hinten verändert.
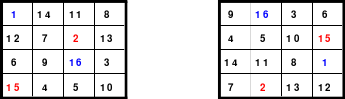
Die Schlüsselzahlen
Mag verwendet bei Berechnungen des Topquadrates neben den genannten mit der Endziffer 9, 7, und weitere auch Schlüsselzahlen die das ein- und mehrfache von 9 sind. Mit diesen Schlüsselzahlen zu rechnen bedeutet keine nennenswerte erhöhte Rechenleistung. Dazu einige Beispiele:
Schlüsselzahl: 9 = 1 * 9 = 9 = 10 - 1
18 = 2 * 9 = 18 = 20 - 2
27 = 3 * 9 = 27 = 30 - 3
36 = 4 * 9 = 36 = 40 - 4
und größere Schlüsselzahlen
108 = 12 * 9 = 108 = 110 – 2 (nahezu wie 109 (110-1))
198 = 22 * 9 = 198 = 200 - 2
Sicher stellen Sie die Frage wozu derartige Schlüsselzahlen?
Bei einer Zahlenvorgabe für 2 Zellen, kann es vorkommen, dass diese eine zu kleine Differenz haben um die gewohnten Rechnungen durchzuführen. Will man keine Änderung einer Zahl verlangen, so muss mit den Vorgaben gearbeitet werden. Diese können auch zu klein sein, um bis zu 7 mal 9 abzuziehen um die Zahl für die Zelle 1 zu ermitteln. In beiden Fällen kann z. B. auf das Duo 4/13 oder 5/12 zugegriffen werden. Dabei kann es zu doppelten Zahlen kommen, was zu vermeiden ist.
Dazu eine mathematische Regel, die Mag nicht weiter beweisen muss. Von der Richtigkeit können sich Zweifler durch Versuche überzeugen.
Wenn die Differenz zwischen 2 Zahlen nicht durch die Schlüsselzahl teilbar ist, werden keine doppelten Zahlen entstehen, wenn diese um das 1- oder mehrfach der Schlüsselzahl erhöht oder vermindert werden.
Um zu prüfen. ob die Entstehung doppelter Zahlen möglich ist, wird geprüft ob die Differenz der beiden Vorgaben durch die Schlüsselzahl geteilt werden kann. Das wird selten der Fall sein. Nur wenn dies zutrifft kann es zu doppelten Zahlen kommen. Wenn die Teilbarkeit nicht gegeben ist, kann es möglicherweise zu einer dichten Annäherung von Zahlen kommen, wobei die Differenz auch 1 sein kann. Doppelte Zahlen sind jedoch ausgeschlossen und die eventuell fast gleichen Zahlen müssen in Kauf genommen werden.
Der Rest
Wie erläutert, beträgt bei einem Topquadrat die Summe eines Duos die Hälfte der magischen Summe und wird folglich durch Division der Vorgabe durch 2 ermittelt. Das bedeutet, dass nur bei einer ungeraden Vorgabe ein Rest von 1 entstehen kann. Normalerweise wird der Rest einem Block zugeschlagen. Damit wird gesichert, dass in jeder Reihe des Quadrates der Rest einmal wirksam wird. Da aber dass Topquadrat nur ein teilhomogenes Quadrat ist, kann die Forderung nicht in jedem Fall erfüllt werden.
1 2 3 4 
Im Quadrat 1 sind die Zellen des 4. Blockes so verteilt, dass in jeder Reihe eine der Zahlen von 13 bis 16 enthalten ist. Das ändert sich auch nicht, wenn 2 Zeilen und/oder Spalten verschoben werden, wie Quadrat 2 zeigt.
Wird jedoch eine ungerade Anzahl von Zeilen und/oder Spalten verschoben, so befinden sich diese Zellen nicht mehr wie gefordert verteilt. Quadrat 3 zeigt die Situation nach Versetzen der unteren Zeile nach oben und anschließend 2 Spalten von vorn nach hinten. Es ist zwar in jeder Zeile und jeder Spalte je eine Zahl von 13 bis 16 vorhanden, aber nicht in den Diagonalen. Damit ist das Quadrat nicht mehr magisch.
In diesem Fall muss der Rest den Zellen zugeordnet werden, die der 1. Block normalerweise einnimmt, egal welche Zahlen sich in diesen Zellen befinden. Quadrat 4 zeigt diese Situation.
Ist der Rest nicht größer als die Differenz zwischen den Zahlen des Quadrates, kann dieser auch jedem beliebigen Block zugeschlagen werden.
Um das Problem der Verteilung des Restes zu umgehen, sollte auf eine Veränderung des Grundquadrates verzichtet werden. Das bedeutet, dass das Publikum keine Zelle vorschlägt, mit der begonnen werden soll, es sei denn, Sie sind so qualifiziert, dass Sie auch diese Hürde nehmen können.
Pandiagonal
Das Topquadrat ist nicht 100%ig homogen. Die Folge ist, dass in einigen Fällen nach einer Berechnung das Quadrat nicht mehr pandiagonal ist.
Die Pandiagonalität ist jedoch wichtig, wenn z. B. die Nennung einer Zelle, mit der begonnen werden soll, erfolgen soll, was als eine Steigerung der Schwierigkeit angesehen wird.
Bekannt ist, dass die Pandiagonalität erhalten bleibt, wenn sich die Zahlen geradlinig um eine gerade Zahl verschieben. Das trifft auf die blauen und weißen Zellen im mittleren Quadrat zu. Einfacher heißt das, solange die Verschiebungen diagonal erfolgen, bleibt das Quadrat pandiagonal. Diese Kenntnis ist aber nur anwendbar, wenn man selbst eine Verschiebung vorsieht. (Siehe mittleres Quadrat)
Interessant ist die Frage, unter welchen Bedingungen das Quadrat pandiagonal bleibt. Es bleibt pandiagonal wenn folgende Bedingungen erfüllt werden:
- Der Multiplikator muss für alle Zellen einheitlich sein.
- Die Summanden müssen für die Blöcke 1 und 2, sowie für die Blöcke 3 und 4 jeweils einheitlich sein.
- Die Übergänge von Block 1 zu 2 und 3 zu 4 müssen gleiche Größe haben. Für den Übergang von Block 2 zu 3 trifft das nicht zu.
Ein Beispiel zeigt das linke Quadrat. Es ist pandiagonal und bleibt es, wenn z. B. nur 1 Spalte verschoben wird. (Siehe Quadrat rechts.)
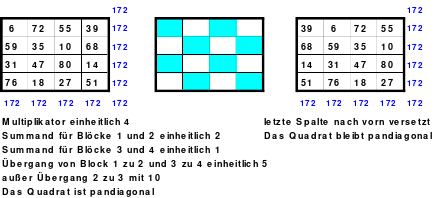
Dies Erkenntnisse können genutzt werden durch:
- Verteilung gerader Reste auf die Blöcke 1 und 2, oder 3 und 4 zu je der Hälfte des Restes.
- Nutzung der Duo-Methode, weil dabei nur mit 2 Blöcken, 1 bis 8 und 9 bis 16, gearbeitet wird.
- Anwendung von Methoden bei denen kein Rest anfällt. (z. B. “Einfach Clever”.)
- die Bitte um Benennung der Zelle mit der begonnen werden soll, wenn die Vorgabe der magischen Summe eine gerade Zahl ist und weitere.
Die Quattros
Das Topquadrat kann in beliebige Quattros, das sind 2 mal 2 = 4 Zellen große Quadrate, geteilt werden. Diese können natürlich niemals magisch sein. Sie haben aber als Summe der 4 Zahlen stets die magische Summe des Gesamtquadrates. Die Quadrat 1 bis 4 zeigen dies.
Das ändert sich auch nicht, wenn beliebige Zeilen und/oder Spalten versetzt werden, wie es das Quadrat 5 beweist. In diesem sind 2 Zeilen und eine Spalte verschoben worden.
Allerdings gibt es auch bei den Quattros Probleme wegen der nicht 100-pozentrigen Homogenität. So fehlen im grünen Quattro des 4. Quadrates, Zahlen des 1. und 4. Blockes. Im blauen Quattro fehlen dagegen Zahlen des 2. und 3. Blockes. Daraus können Probleme bei der Zuordnung eines Restes entstehen. Deshalb sollte hier auf die Vorgabe einer magischen Summe verzichtet werden.
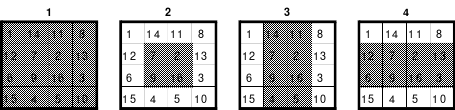
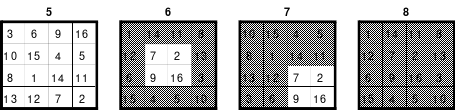Im Quadrat 6 wird gezeigt, dass alle
Zellen, die durch Versetzen von Reihen ein Quattro bilden können,
ebenfalls die magische Summe haben. Der Beweis ist das Quadrat 7. Hier
wurde die letzte Spalte nach vorn und die unterste Zeile nach oben
versetzt.
Zum Schluss noch eine Betrachtung zum Quadrat 8. Hier sind die Summen aller 4 Zahlen, die symmetrisch eingeordnet sind, ebenfalls gleich der magischen Summe. Das muss so sein, denn wie Sie richtig erkannt haben, handelt es sich dabei um jeweils 2 Duos mit der Duosumme 17.
Mag wird mit den Experimenten “4 im Zentrum”, “Das Quartett” und “Das Quattroquadrat” Beispiele einer Anwendung dieser Regeln zeigen.
6.3.2. Das kleine Hexen 1x1
Im kleine Hexen 1x1 wird die Bildung von magischen Quadraten mit kleinen Zahlen beschrieben, wobei einfache Regeln der Multi- und Duomethode zum Aufbau der Quadrate genutzt werden. Sie bilden auch die Grundlage für den Einsatz größerer Zahlen und werden auch in den anderen Disziplinen wie “Hohe Schule” und “Sonderquadrate” angewendet, allerdings in oft verschleierter Form.
Die “Hohe Schule” unterscheidet sich in der Art und Weise der Eintragung der Zahlen in die Zellen. Sie werden zeilenweise eingetragen, was besonders für größere Quadrate wie 5. und 7. Ordnung nicht einfach zu lösen ist. Bei kleineren Quadraten ist der Aufbau des Grundquadrates auswendig zu erlernen. Auch ist der Rechenaufwand etwas größer. Diese Quadratbildung ist eleganter und lässt die Methode der Art und Weise des Quadrataufbaus nur schwer erkennen.
Die Sonderquadrate sind ausgewählte Quadrate, die schwerer zu realisieren sind und oft von den Grundvarianten der Berechnung abweichen. Dazu gehören Doppelvorgaben, Primzahlenquadrate, Königsquadrate, Austauschquadrat und weitere. Die Sonderquadrate werden im Inhaltsverzeichnis einzeln aufgeführt und auch einzeln beschrieben. Sie sind in der Regel schwerer zu realisieren und stellen höhere Anforderungen an den Vorführenden.
Doch nun zum kleinen Hexen 1x1.
Vorgabe einer Zahl für eine Zelle
Auf der Tafel ist ein leeres Quadrat der 4. Ordnung aufgezeichnet. Mag bittet um eine 2-tellige Zahl. Es wird 67 genannt, die er in eine Zelle einschreibt. Nach einer sehr kurzen Denkpause schreibt er über das Quadrat die Zahl 322. Anschließend trägt er in einer scheinbaren Unordnung Zahlen in die leeren Zellen ein. Nach Fertigstellung des Quadrates erklärt er, dass das Quadrat ein magisches ist, bei dem die Summen aller Spalten, Zeilen und Diagonalen einheitlich 322 betragen die er vorherberechnet und über das Quadrat geschrieben hat.
Das so gebildete Quadrat ist das Quadrat 2. Das Quadrat 1 ist das Topquadrat um die Berechnungen besser zu verfolgen.
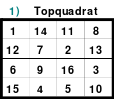
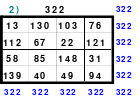
Die Lösung
Gleich vorweg: Das Topquadrat muss auswendig erlernt sein! Sonst geht nichts!
Als die Zahl 67 genannt wurde, hat Mag diese durch 9 geteilt und 7 mit Rest 4 errechnet. Die 9 ist die Schlüsselzahl, die Mag gewählt hat. Die berechnete 7 ist die Zelle, in die die 67 einzusetzen ist.
In der Folge werden alle Zellenzahlen mit 9 multipliziert und der Rest 4 zugeschlagen. Die magische Summe wird ebenso berechnet.
Das ist die magische Summe des Grundquadrates mal 9 + 4*4. Der Rest muss 4-mal zuaddiert werden, da jede Reihe des Quadrates 4 Zahlen enthält. Das ist bei der Vorgabe 67 und der magischen Summe des Grundquadrates von 34:
34*9 + 4*4 = 306 + 16 = 322,
die über das Quadrat geschrieben wird.
Dann folgt Zelle 1, in die 1*9 + 4 = 13 kommt.
In die Zelle 2 kommt 2*9 + 4 = 22
Vergleicht man beide Berechnungen, so ergibt sich, dass die folgende Zelle lediglich um 1*9 = 9 erhöht wird. Das kann ausgenutzt werden, in dem von Zelle 1 aus, in die folgenden Zellen jeweils eine um 9 erhöhte Zahl eingesetzt wird.
Das wäre im Beispiel: In Zelle 2 wird 13+9 = 22 eingeschrieben, in Zelle 3: 22+9 = 31, in Zelle 4: 31+9 = 40 usw. bis zur Zelle 16, in die dann 139+9 = 148 einzusetzen ist und fertig ist das Quadrat.
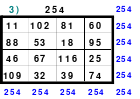
Das Quadrat 3 wurde mit der Schlüsselzahl 7 gebildet.
Die Zelle für die Zahl 67 ist dann: 67/7 = 9, Rest 4.
In die Zelle 1 ist einzusetzen: 1*7 +4 = 11.
Die Zahlen für die übrigen Zellen werden durch Erhöhung der vorangegangenen Zahl um 7 ermittelt.
Die magische Summe wurde mit 34*7+4*4=254 ermittelt.
Eine Nachbetrachtung
Die Berechnungen erfolgten nach der Multimethode. Alle Zellen wurden gleichbehandelt. Sie wurden mit 9 multipliziert und um 4 erhöht.
Damit sind die Bedingungen für ein pandiagonales Quadrat erfüllt und es können beliebige Spalten und/oder Zeilen versetzt werden.
Das bedeutet auch, dass die berechnete Zelle als 1. in der 1. Zeile eingesetzt werden kann. In der weiteren Folge werden die Zahlen für die Zellen in der gleichen Zeile nacheinander einzeln berechnet, das entspricht der “Hohen Schule”.
Konkret wird im Beispiel aus Zelle 1 die Zelle 7.
Die nächste Zelle ist die Zelle 2 (rechts von der 7), folglich wird 2*9+4 = 18+4 = 22 in diese eingetragen.
Weiter folgt Zelle 13 (rechts von der 2), in die 13*9 +4 =117+4 = 121 kommt und in die letzte Zelle dieser Zeile, die Zelle 12, kommt 12*9+4 = 108+4 = 112.
Die nächste Zeile beginnt mit der Zelle 9, die im Grundquadrat unter der Zelle 7 angeordnet ist. Hier wird 9*9+4 = 81+4 = 85 eingetragen.
So wird jede Zelle bearbeitet bis das Quadrat fertig ist.
Es ist das Quadrat 4.
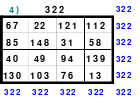
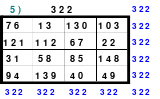
Die Qualitätssteigerung erfordert nur eine etwas schwerere Berechnung, die kein Problem sein dürfte.
Kein Problem ist es dann auch nicht, wenn die Zuschauer die Zelle bestimmen, mit der begonnen werden soll, wie im Beispiel im Quadrat 5, wo die 3. Zelle in der 2. Zeile, als Beginn bestimmt wurde. Diese Variante entspricht einer Doppelvorgabe, denn es wurden die Zahl und die Zelle mit der begonnen werden soll vorgegeben.
Eine Erläuterung zur Abarbeitung dazu dürfte sich erübrigen.
Trotzdem ein kleiner Hinweis:
Bearbeiten Sie nur den rechten Teil der Zeile in die die Vorgabe eingesetzt wurde, und gehen Sie dann zur nächsten Zeile. Das entspricht einer normalen Schreibweise, was jedoch nicht bindend ist. Die Fertigstellung der Beginnzeile erfolgt dann zum Schluss.
Vorgabe der magischen Summe
Die von Mag erbetene 3-stellige Zahlenvorgabe 723 hat er über das noch leere Quadrat geschrieben. Anschließend folgten die Eintragungen unterschiedlicher Zahlen, in einer unregelmäßigen Form, in die noch leeren Zellen.
Das fertige Quadrat ist magisch mit der vorgegebenen magischen Summe von 723.
Es ist das Quadrat 2.
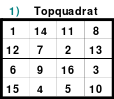
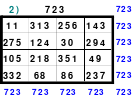
Die Lösung
Zur Lösung wurde die Duomethode angewendet.
Damit entsprechen die Duosummen der halben Vorgabe.
Als Duo wird das Duo 16/1 festgelegt.
Die Duoreihen sind die Zellen 1 bis 8 als aufsteigende Zahlenreihe und 16 bis 9 als absteigende Zahlenreihe.
In die Zelle 16 wird aber nicht ganz die Hälfte 723/2 = 361 eingesetzt, sondern 361-10 = 351. Die abgezogene 10 wird in Zelle 1 eingetragen und zusätzlich um den Rest 1 auf 11 erhöht.
Als Nächstes muss die Schlüsselzahl bestimmt werden. Sie muss gleich oder kleiner ein 16-tel der Summe in Zelle 16 sein. Das ergibt sich theoretisch aus der Tatsache, dass die Schlüsselzahl 16-mal abgezogen werden muss und eine positive Zahl für die Zelle 1 verbleiben muss. Das ist 351/16 = abgerundet 22. Als Schlüsselzahl hat Mag die 19 gewählt, das ist auch 20-1, womit leichter gerechnet werden kann.
Jetzt können die restlichen Zellen mit Zahlen ausgefüllt werden.
Als erstes sollte die absteigende Reihe berechnet werden. Die Zelle 15 ist um 1 kleiner als 16, deshalb wird 351-19 = 332 in diese eingesetzt. Es folgt Zelle 14 mit 332-19 = 313, Zelle 13 mit 313-19 = 294 usw. bis zur Zelle 9, in die als Zahl 218 kommt.
Dann folgt die aufsteigende Reihe mit der Zelle 2, die um 1 größer als 1 in der 1. Zelle ist. In die Zelle 2 ist 11+19 = 30 einzusetzen.
Es folgt Zelle 3 mit 30+19 = 49, Zelle 4 mit 49+19 = 68.
Achtung!
Der Rest = 1 darf nur einem Block zugeschlagen werden. Da in die Zelle 1 der Rest 1 eingerechnet wurde und in die Zellen 2 bis 4 mitgenommen wurden, ist die Aufgabe erfüllt. Das heißt, die Zahl in Zelle 5 wird nicht nur um 19 erhöht, sondern es muss der Rest von 1 wieder abgezogen werden. In die Zelle 5 wird deshalb die Zahl 68+19-1 = 86 eingetragen.
In der weiteren Folge wird dann nur noch 19 zuaddiert. Für Zelle 6 ist das 86+19 =105, für Zelle 7 ist es 105+19 = 124 und in die letzte noch offene Zelle 8 kommt 124+19 = 143.
Damit ist das Quadrat fertig.
Eine Nachbetrachtung
Das Ergebnis ist sehr gut und ansehnlich. Mängel können nicht genannt werden. Trotzdem können Fragen gestellt werden: Warum wird die 1. Zahl irgendwo im Quadrat eingesetzt? Wieso wird in die Zelle 1 eine so kleine Zahl geschrieben? Weshalb werden die Zahlen nicht der Reihe nach eingeschrieben? Warum sind die Zahlen jeweils um den gleichen Betrag erhöht bzw. vermindert?
Auf diese Fragen muss nicht eingegangen werden, denn sie sind belanglos. Mag hat die gleiche Einstellung, meint aber, dass Verbesserungen nicht unbedingt abzulehnen sind und beschreibt die Variante
Hohe Schule
Dazu werden 2 Zeilen des Topquadrates von unten nach oben und 2 Spalten von vorn nach hinten versetzte. Es ist das Quadrat 4. (Siehe weiter unten)
Da eine gerade Anzahl von Reihen versetzt wurde, bleibt das Quadrat magisch, auch wenn ein Rest eingeordnet werden muss.
Die Zelle 16 ist jetzt die 1. in der 1. Zeile, in die die Zahl 351 kommt. Die Zelle 1 befindet sich 2 Zellen diagonal von Zelle 16. Die Zahl 11 für Zelle 1 wird aber noch nicht eingesetzt, sondern die muss man sich merken.
Wegen der Veränderung des Topquadrates wird es nicht mehr so leicht sein, zum Beispiel die Zelle 15 zu finden. Die Zeilen und Spalten sind zwar ebenfalls verändert, aber hier ist die Reihenfolge leichter zu rekonstruieren, was die Grundlage für eine zeilenweise Eintragung der Zahlen ermöglicht.
So ist im unveränderten Quadrat rechts von der Zelle 16 die Zelle 3 zu finden.
3 ist um 2 größer als 1. Deshalb wird in diese 11+2*19=49 geschrieben. Die 3. Zelle ist im Quadrat ganz rechts. Folglich wird von links fortgesetzt. Hier ist die 6 die 1. Zelle und um 5 größer als 1. Die Zelle 5 gehört zum 2. Block die nicht mehr mit dem Rest 1 belastet werden darf. weshalb hier 11+5*19 = 106-1 = 105 einzusetzen ist.
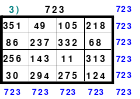
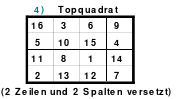
Im Grundquadrat befindet sich rechts von der 6 die 9. Die 9 gehört zur absteigenden Zahlenreihe und ist um 7 kleiner als 16. Die Zahl für Zelle 9 ist somit
351-7*19 = 351- 140+7 = 211+7 = 218.
Jetzt geht es zur nächsten Zeile. Unter der 16 befindet sich die 5 im Grundquadrat. In diese Zelle kommt 11+ 4*19-1 = 86.
Rechts der Zelle 5 befindet sich die Zelle 10, die zur absteigenden Zahlenreihe gehört. Die Zahl für Zelle 10 wird 351-6*19 = 351-120+6 = 231+6 = 237.
So wird weiter gerechnet bis das Quadrat fertig ist.
Es ist das Quadrat 3. Dieses ist magisch mit der magischen Summe von 723.
Die “Hohe Schule” ermöglicht eine weitere Verbesserung der Darbietung.
Wird eine gerade Zahl als magische Summe vorgegeben, so entsteht kein Rest und die Zuschauer können zusätzlich die Startzelle vorgeben. Das entspricht einer Doppelvorgabe und hat einen zusätzlichen Showeffekt. Die vorgegebene Startzelle ist für Sie die Zelle 16. Die Berechnungen erfolgen wie beschrieben.
Zugegeben, die besserte Qualität der “Hohen Schule” wird der einfacheren Lösung geopfert.
Aber es steht Ihnen ja frei, bei der einfacheren Lösung zu bleiben.
Kleine Tricks die Sie kennen sollten.
Das 19 = 20-1 ist wurde bereits gesagt. Wird bei der Berechnung der absteigenden Zahlenreihe 19 abgezogen, so ist das auch -20+1. Es werden zuerst 20 abgezogen und dann um 1 erhöht.
Zur Ermittlung der Schlüsselzahl muss die Zahl in Zelle 16 durch 16 geteilt werden, was im ungünstigen Fall nicht leicht zu machen ist. Einfacher und nur etwas weniger genau ist folgende Berechnung. Da 100/16 = 6,2 ist, werden die Hunderter mit 6 multipliziert und die Zehner ebenso, jedoch durch 10 geteilt, indem die letzte Ziffer gestrichen wird. Beide Ergebnisse addiert, ergibt den Wert aus dem die Schlüsselzahl bestimmt werden kann. Das ist bei der Zahl 351 in Zelle 16: 3*6 = 18 + 5*6/10 = 18+3 = 21. Die so errechnete Zahl ist lediglich um 1 kleiner als die genau berechnete.
Die 3-stellige Vorgabe der magischen Summe muss mindestens 102 sein, um die kleinste Schlüsselzahl 3 zu erhalten. (102/2 = 51 -1 (für Zelle 1) = 50 >> 5*6 = 30 reduziert =3)
Eine so kleine Zahl wird wohl kaum genannt werden. Werden kleine Vorgaben gemacht, so sollte geprüft werden ob die Zahlen in den Zellen 1 und 16 beide gerade oder ungerade sind. Sind diese unterschiedlich kann eine doppelt so große Schlüsselzahl gewählt werden, die aber eine gerade sein muss. So könnte statt der 3 die 6 als Schlüsselzahl gewählt werden, ohne dass es zu doppelten Zahlen kommen kann.
Die Zahl für Zelle 1 hat Mag mit 11 festgelegt. Hier kann jeder Wert eingesetzt werden, was z. B. bei Wiederholungen erforderlich ist. So kann ganz einfach nur der Rest zum Einsatz kommen. Ist kein Rest vorhanden wird die Zahl in Zelle 16 um eine frei gewählte Größe reduziert und der reduzierte Wert kommt in Zelle 1. Bei der Wahl ist Feingefühl gefragt, denn die Zahl für Zelle 1 sollte bei kleinen Vorgaben nicht zu groß sein und umgekehrt bei großen Vorgaben nicht zu klein. Geeignet sind kleinere 2-stellige Zahlen, die sich gut merken lassen.
Mag hat Mehrfachvorgaben nicht in das “Kleine Hexen 1x1” aufgenommen, da es in der Regel höhere Anforderung abverlangt.
Doppelvorgaben sind bereits Vorgaben, die zusätzlich mit einer Vorgabe der Startzelle verbunden werden. Dazu hat Mag im kleinen 1x1 Beispiele genannt.
Schwieriger sind Doppelvorgaben von Zellenzahlen, gekoppelt mit der Vorgabe einer magischen Summe, oder Vorgaben von 2 Zellenzahlen.
Mag hat einige Beispiele in seine Ausführungen aufgenommen.
Alle Lösungen können aus der Duomethode und/oder der Quadratstruktur abgeleitet werden.
Start mit 2 Duos
Mag hat das Beispiel mit dem Duo 1/16 beschrieben.
Zwar keine Probleme, aber kleine Nachteile wurden bereits genannt. So müssen 7 Zahlen als aufsteigende und 7 Zahlen als absteigende Zahlen berechnet werden. Die regelmäßige Erhöhung oder Minderung der Zahlen um die Schlüsselzahl kann auffällig werden, besonders wenn die Vorgabe klein und folglich auch die Schlüsselzahl klein ist. Mit einem Achtung hat Mag darauf aufmerksam gemacht, dass der in der Zelle 1 enthaltene Rest nicht mit in den folgenden Block übernommen werden darf. Wird das vergessen, entsprechen die Summen nicht der Vorgabe. Günstig ist die so genannte Startphase zusätzlich mit dem Duo 8/9 zu bilden. Das bringt nur Vorteile und kann ganz einfach realisiert werden, was nachfolgend an einem Beispiel erklärt wird.
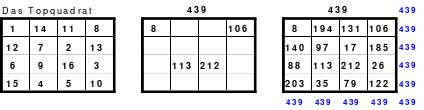
Die Vorgabe ist 439. Die Vorgabe wird durch 2 geteilt und das Ergebnis 219, Rest 1 ermittelt. 219 ist zugleich die Duosumme. Die Duosumme wird leicht gekürzt in die Zelle 16 eingesetzt. Im Beispiel wurde die Kürzung mit 7 gewählt. Somit kommt in Zelle 16 219-7 = 212. In die Zelle 1 wird der Rest 1 und zusätzlich die Kürzung, das ist 1+7 = 8, eingetragen.
Die Kürzung ist ein kleiner Trick, mit dem die folgenden Berechnungen erheblich erleichtert werden. Wenn die Vorgabe eine gerade Zahl ist, dann entsteht kein Rest. Um in die Zelle 1 eine positive Zahl einzusetzen, wäre eine Kürzung der Duosumme ohnehin notwendig. Durch die Kürzung kann die Zahl in Zelle 1 erhöht werden.
Es steht die Frage, wie groß sollte die Kürzung sein?
Sie sollte in etwa der Schlüsselzahl entsprechen, weil dann die Differenz zwischen den Duozahlen des Duos 8/9 den allgemeinen Differenzen entsprechen. (Das wird noch näher erklärt!)
Wichtig ist, dass die Kürzung so gewählt wird, dass die Zahl in Zelle 16 eine gerade wird. Im Beispiel wurde die Duosumme 219 um 7 gekürzt und 212 als gerade Zahl in die Zelle 16 eingetragen. Die 8 (Zelle 8) ist die Hälfte von 16 (Zelle 16), Die Zahl für Zelle 8 wird durch Halbierung der Zahl in Zelle 16 ermittelt. Das ist 212/2 = 106. Dabei kann kein Rest mehr entstehen, der zusätzlich behandelt werden müsste.
In die Zelle 9 muss die Differenz zwischen der Duozahl und der Zahl in Zelle 8 eingesetzt werden, damit die Summe der Duosumme entspricht. Das wird ganz einfach erreicht, indem die Zahl in Zelle 8 um die Kürzung erhöht wird, also 106+7 = 113 für Zelle 9. (106+113 = 219, die Duosumme.)
Das mittlere Quadrat zeigt diesen Bearbeitungsstand.
Was wurde erreicht?
Die 4 Zahlen gehören zu je einem der 4 Blöcke und zwar 2-mal als 1. Zahl (8 und 113) und 2-mal als die 4. Zahl (106 und 212).
Von diesen ausgehend werden die restlichen 3 Zahlen der Blöcke als auf- oder absteigende Reihe berechnet und eingeschrieben. Die Schlüsselzahl dazu ist 4*3 = 12, gewählt 9. Es wird empfohlen abwechselnd eine auf- und absteigend Reihe zu bearbeiten. Der Rest muss nicht mehr beachtet werden.
Das Endergebnis ist das rechte Quadrat.
6.3.3. Doppelvorgaben
Die hohe Schule *
Auf der Tafel ist ein leeres Quadrat der 4. Ordnung aufgezeichnet.
Mag bittet einen Zuschauer um Nennung einer zweistelligen Zahl. Es wird 79 genannt. Nun bittet er um Bestimmung der Zelle, in die die Zahl eingeschrieben werden soll. Es wird die 3, Zelle in der 2. Zeile gewählt, in die Mag die Zahl 79 einsetzt.
Einen weiteren Zuschauer bittet er ebenfalls um eine 2-stellige Zahl. Dieser nennt 48, die Mag in eine andere Zelle einsetzt.
Nach einer sehr kurzen Überlegung schreibt Mag über das Quadrat die Zahl 254.
Anschließend füllt er das Quadrat mit unterschiedlichen Zahlen aus. Dabei beginnt er hinter einer der vorgegebenen Zahlen, wobei er die Zahlen zeilenweise einschreibt.
Ist das Quadrat fertig, erklärt er, dass die Addition der 4 Zahlen jeder Zeile, Spalte und der Diagonalen die Summe von 254 ergibt, was er vorher über das Quadrat geschrieben hat. Die Jury kann diese Aussage nach Prüfung bestätigen.
Es ist das Quadrat 3
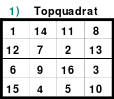
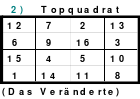
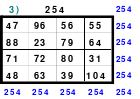
Die Lösung
Zur Lösung dieser Aufgabe wird die Duomethode eingesetzt.
Die 1. Vorgabe 79 wird wie gefordert in die 3. Zelle der 2. Zeile eingetragen.
Die 2. Vorgabe 48 kommt in die Zelle die sich 2 Zellen diagonal zur 1. befindet. Das ist die 1. in der 4. Zeile. Beide Zahlen bilden dadurch ein Duo, deren Duosumme 79+48 = 127 ist. Bei Quadraten der 4. Ordnung ist die Duosumme halb so groß wie die magische Summe. Deshalb wird die magische Summe berechnet, indem die Duosumme verdoppelt wird, das ist 127*2 = 257, die über das Quadrat geschrieben wird.
Nun werden die Zellen für das Duo festgelegt. Da die 48 in einer ersten Zelle ist, wird diese als die Zelle 1 bestimmt. Die Zelle mit der Zahl 79 wird damit die Zelle 16.
(Es können auch andere Festlegungen getroffen werden. Das ist abhängig von den Vorgaben. Ein Beispiel dazu wird im Experiment “Das Quattroquadrat” beschrieben.)
Mag bestimmt die 48 als 1. Zahl in der aufsteigenden und die 79 als 1. Zahl in der absteigenden Zahlenreihe und als Schlüsselzahl 8. Diese Wahl ist zulässig, da nicht beide Vorgaben eine gerade oder ungerade Zahl sind und von 79 der Wert 8*8 = 64 abgezogen werden kann. Es können dem zufolge keine doppelten oder negativen Zahlen entstehen. Auch können die Zahlen nicht einheitlich gerade oder ungerade werden.
(Natürlich hätte auch die 9 als Schlüsselzahl gewählt werden können. Dann hätte aber geprüft werden müssen, ob die Differenz zwischen den beiden Vorgaben durch 9 teilbar ist.)
Im Beispiel sind die Dualzahlen günstig eingesetzt. Sie erfordern lediglich die Verschiebung der oberen Zeile mit der 1 nach unten, wie es das Quadrat 2 zeigt.
Die Eintragung der restlichen Zahlen erfolgt nach der “Hohen Schule”, also zeilenweise. Begonnen wird ab der Vorgabe 48, die sich in Zelle 1 befindet.
Die nächste Zelle ist, immer bezogen auf das Grundquadrat, die Zelle 14 und gehört zur absteigenden Zahlenreihe. 14 ist um 2 kleiner als 16, weshalb von der Zahl 79 in der Zelle 16 die Schlüsselzahl 2-mal abgezogen werden muss.
Das ist 79-2*8 = 79-16 = 63, die in die 2 Zelle der untersten Zeile eingetragen wird.
Die nächste Zelle ist die Zelle 11, die ebenfalls zur absteigenden Zahlenreihe gehört.
11 ist um 5 kleiner als 16, weshalb in diese Zelle 79-5*8 = 79-40 = 39 kommt.
Als nächste Zelle kommt die 8. Diese ist eine Zahl der aufsteigenden Zahlenreihe und um 7 größer als 1. Also wird in diese Zelle 48+7*8 =48+56 = 104 geschrieben.
Damit ist die unterste Zeile fertig und es wird mit der obersten fortgefahren.
Unter der Zelle 1 befindet sich die Zelle 12, mit der begonnen wird.
Die 12 gehört zur absteigenden Zahlenreihe und ist um 4 kleiner als 16, weshalb
79-4*8 = 79-32 = 47 in diese einzusetzen ist.
So wird weiter verfahren, bis das Quadrat fertig ist.
Das Quadrat ist pandiagonal, da ja kein Rest anfällt, der ja nur bei ungeraden Vorgaben einer magischen Summe entstehen kann.
Eine Nachbetrachtung
Natürlich können auch größere Zahlen vorgegeben werden, aber nach Möglichkeit auch keine größeren als 3-stellige.
Vorteilhaft ist z. B. die Vorgabe einer 2-stelligen und einer 3-stelligen Zahl. Diese haben in der Regel eine größere Differenz, wodurch eine Prüfung auf Teilbarkeit entfallen kann. Auch sind die Zuordnung eines Duos und die Festlegung der Schlüsselzahl einfacher.
Das Quattroquadrat *
Auf der Tafel ist ein leeres Quadrat der 4. Ordnung aufgezeichnet.
Mag bittet einen Zuschauer um Nennung einer zweistelligen Zahl. Es wird 27 genannt. Nun bittet er um Nennung der Zelle in die die Zahl eingesetzt werden soll. Die 2, Zelle in der 3. Zeile wird gewählt, in die Mag die Zahl 27 einsetzt.
Einen weiteren Zuschauer bittet er ebenfalls um eine 2-stellige Zahl. Dieser nennt 36, die Mag in eine andere Zelle einsetzt.
Nach einer sehr kurzen Verzögerung schreibt Mag über das Quadrat die Zahl 126.
Anschließend füllt er das Quattro oben rechts mit unterschiedlichen Zahlen aus. Ist das erfolgt, erklärt er, dass die Addition der 4 Zahlen die Summe von 126 ergibt, was er vorher über das Quadrat geschrieben hat. Die Jury kann diese Aussage nach Prüfung bestätigen.
In gleicher Weise folgen die Quattros unten links, in der Mitte, Oben links und unten rechts. Die nachfolgenden Abbildungen zeigen den Ablauf im Einzelnen.
(Die grüne Schattierung dient nur zur Unterstützung der Erläuterungen.)
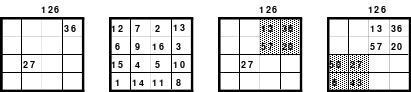
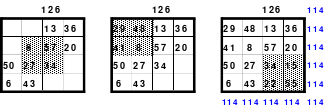
Nach jeder Fertigstellung eines Quattros gibt Mag seine Erklärung zur Summe 126 ab und bittet die Jury um Kontrolle.
Erst zum Schluss trifft er die Aussage, dass das so entstandene Quadrat ein magisches ist, bei dem alle Zeilen, Spalten und auch Diagonalen die einheitliche Summe von 126 haben und keine Zahl doppelt vorkommt.
Des Weiteren ist das Quadrat im Gegensatz zu den Quadraten mit 4 Zahlen als Vorgabe pandiagonal. Der Grund ist, dass nur 2 Blöcke vorhanden sind.
Die Lösung
Die Lösung beruht auf Regeln, die bereits erläutert wurden. Zur Vertiefung der Kenntnisse wird nochmals darauf eingegangen.
Im Topquadrat haben alle 2 mal 2 Zellen große Quattros als Summe der 4 Zahlen die magische Summe von 34.
Alle Duos haben zueinander den gleichen Abstand. Er beträgt 2 Zellen diagonal. Im Quadrat gibt es immer nur eine Lösung dafür.
An diesen Regeln ändert sich nichts, wenn das Topquadrat durch Verschiebung von Zeilen und/oder Spalten verändert wird.
Das ist in den beiden Quadraten deutlich erkennbar. Links das Topquadrat und rechts das Topquadrat nach Verschiebung von 2 Zeilen nach unten und die letzte Spalte nach vorn. Das Duo 1/16 ist hervorgehoben.
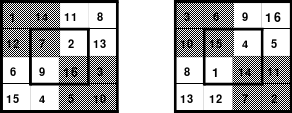
Die erste Zahl 27 wird in die vorgegebene Zelle eingesetzt.
Die zweite Zahl 36 wird als die 2. Duozahl eines Duos 2 Zellen diagonal in die Zelle oben rechts eingeschrieben.
Es ist bekannt, dass die magische Summe in einem Quadrat der 4. Ordnung das 2-fache der Duosumme ist. Da die Zahlen 27 und 36 ein Duo bilden, hat Mag beide Vorgaben addiert und anschließend mit 2 multipliziert. Damit war die magische Summe mit der Größe 27+36 = 63 und 63*2 = 126 gefunden.
Als nächstes wird die Schlüsselzahl mit 9 festgelegt. Es muss aber geprüft werden ob das möglich ist. Dazu wird die Differenz der beiden Vorgaben auf die Teilbarkeit durch 9 geprüft. Die Differenz 36-27 = 9 ist durch 9 teilbar.
Dieser Umstand kann zu doppelten Zahlen führen, weshalb Mag auf die Schlüsselzahl 7 untereinander befinden, was man immer aus dem Grundquadrat ableiten kann.
Die Berechnung des 1. Quattros oben rechts kann beginnen.
Links neben der Zelle 13 ist die Zell 2. 2 ist um 2 kleiner als 4. Folglich wird von der Zahl in Zelle 4, 2*7 = 14 abgezogen. Das ist 27-14 = 13, die in die Zelle 2 eingesetzt wird.
Unter der Zelle 13 befindet sich die Zelle 3, die zum 1. Block gehört. Hier muss die Zahl in Zelle 4, um 1*7=7 reduziert werden. Das ist 27-7= 20.
Unter der Zelle 2 befindet sich die Zelle 16, die zum 2. Block gehört. Da 16 um 3 größer als 13 ist, muss 3*7 = 21 zur Zahl in Zelle 13, das ist 36, zugeschlagen werden. Das ergibt 36+21 = 57.
Das 1. Quattro ist fertig.
Die anderen Quattros werden analog berechnet. Wenn dabei auf eine bereits berechnete Zahl zugegriffen wird, darf das natürlich nur innerhalb des zugehörigen Blockes erfolgen. Um Fehler zu vermeiden sollte aber immer von den Vorgaben aus der Berechnung erfolgen.
Nach der Berechnung der weiteren Quattros ist das magische Quadrat fertig.
Eine Nachbetrachtung
Dieses Rechenexperiment mit dem Topquadrat kann durchaus als eine exzellente Darbietung eingestuft werden.
Sie erfordern aber auch eine komplexe Denkweise des Vorführenden.
Die umfassenden Berechnungen sind nicht gerade einfach, besonders auch wegen der Ermittlung der Zellen neben, über und unter den Zellen des ermittelten Duos. Deswegen hat Mag diesem Experiment ja auch einen Stern gegeben.
Wem es zum Anfang zu schwer ist, der kann sich die 2-stelligen Zahlen einmal aus dem unteren Bereich und dann aus dem oberen Bereich nennen lassen. Auch kann auf die Vorgabe der Zelle, mit der begonnen werden soll, verzichtet werden.
Die kleinere Zahl wird in die Zelle 1 und die größere in die Zelle 16 eingetragen.
Dann wird mit dem unverändertem Topquadrat gearbeitet.
Die Schlüsselzahl muss so gewählt werden, dass von der Zahl in Zelle 16 noch das 7-fache der Schlüsselzahl abgezogen werden kann, wobei noch ein Rest für die Zelle 9 verbleiben muss.
Und wer es schwerer haben will, der lässt sich größere Zahlen nennen. Dafür müssen jedoch auch größere Schlüsselzahlen gewählt werden.
Das Problem würde bereits auftreten, wenn für die 2. Zahl nicht um eine Zahl zwischen 100 und 200 gebeten wird. Denn auch die Zahl 997 ist eine 3-stellige. Selbst wenn von dieser bis zu 7*9 = 63 abgezogen wird, werden 8 von den 16 Zahlen im Quadrat größer 900 sein, während die 2-stellige Zahl 99 nur auf 162 anwachsen kann. Das Ergebnis wäre eine sehr schlechte Zahlenstreuung. Um das zu vermeiden müssen entsprechend größere Schlüsselzahlen zum Einsatz kommen, die jedoch auch die Berechnungen erschweren.
Die Schlussfolgerung ist, machen Sie es sich nicht schwerer als nötig.
Zum Abschluss
noch eine Variante mit einer 2- und einer 3-stellige Vorgabe, wobei die 3-stellige Vorgabe eine Zahl kleiner 200 sein soll. Damit wird gesichert, dass von der 3-stelligen Zahl auf jeden Fall 8-mal die Schlüsselzahl 9 abgezogen werden kann. Das bedeutet, dass für die Vorgaben die Zellen 1 und 16 gewählt werden können, egal welche Zelle als Beginn vorgegeben wird.
Trotzdem muss geprüft werden, ob es zu doppelten Zahlen kommen kann. Das wird erforderlich, wenn die Differenz zwischen den Vorgaben kleiner 136 ist.
Das ist hier der Fall. Die Differenz beträgt 174-57 = 117 und ist durch 9 teilbar. (Quersumme von 117 ist 9 und damit durch 9 teilbar.)
Deshalb wurde die Schlüsselzahl mit 7 festgelegt.
Die Berechnungen erfolgen im Weiteren nach dem gleichen Prinzip wie anfangs beschrieben.
Die nachfolgenden Quadrate zeigen die einzelnen Arbeitsschritte bis zur Fertigstellung des Quadrates mit der magischen Summe von 462, die auch die Summen der einzelnen Quattros sind.
Dass die Berechnungen mit größeren Zahlen auch etwas schwieriger sind, muss nicht betont werden.
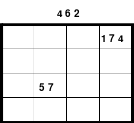
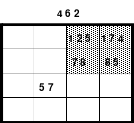
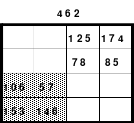
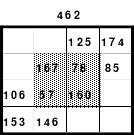
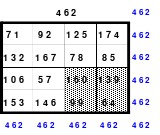
Es bleibt Ihnen überlassen, für welche Variante Sie sich entscheiden.
Mag bevorzugt die Variante mit den zwei 2-stelligen Zahlenvorgaben.
Da in den vorangegangenen Experimenten auch die Zelle für die erste Zahl vom Publikum vorgegeben wurde, kann sogar von 3-fachen Vorgaben gesprochen werden.
Hinweis
Auf eine ausführliche Erläuterung der Bildung eines Quadrates bei Vorgabe einer Zellenzahl und einer magischen Summe wird verzichtet. Sie wurde bereits beschrieben, nur das nicht die magische Summe als 3. Zahl für den Start errechnet wird, sondern die 2. Duozahl, Diese wird durch Abzug der vorgegebenen Zellenzahl von der Hälfte der magischen Summe berechnet. Die vorgegebene magische Summe muss jedoch größer 400 sein, weil die 3-stellige Vorgabe von maximal 200 noch von der Hälfte der Magischen Summe abgezogen werden muss.
Da es sich bei Vorgabe der magischen Summe um eine ungerade Zahl handeln kann, kann auch ein Rest anfallen. Deshalb sollte in diesen Fällen von der Wahl einer Startzelle abgesehen werden. Die Entscheidung dazu erfordert, dass die Vorgabe der magischen Summe als erstes erfragt wird. Dann kann man feststellen ob diese eine gerade Zahl ist oder nicht. Ist sie ungerade entsteht ein Rest und die beiden Duozahlen werden einfach in die Zellen 1 und 16 des unveränderten Grundquadrates eingesetzt.
Die magische Summe sollte eine 3-stellige größer 400 sein. Bei den Zellenzahlen ist eine Vorgabe einer 3-stelligen und einer 2-stelligen Zahl günstig. Dabei sollte die 3-stellige Vorgabe kleiner 200 sein. Die Begründung wurde weiter oben bereits genannt.
Wie der Rest zu behandeln ist, wurde mehrfach beschrieben. Er muss einem 4er Block zugeschlagen werden. Hier bietet sich der Block 2 oder 3 an, weil die beiden Duozahlen in die Blöcke 1 und 4 eingetragen werden.
6.3.4. Das Hexenquadrat * Eine 3-fach-Vorgabe
Bei diesem Experiment gibt das Publikum 3 Zahlen vor, die magische Summe und 2 Zellenzahlen. Die magische Summe soll dabei 3-stellig und größer 500, die 1. Zellenzahl 2-stellig und die 2. Zellenzahl 3-stellig, jedoch kleiner 200 sein. Diese Begrenzung ist notwendig um 2 mal 2 Duopaare zu bilden, wobei die Summe der einzelnen Duos die Hälfte der magischen Summe bekanntlich nicht überschreiten darf. Anderenfalls kommt es zu negativen Zahlen.
Der Einsatz größerer Zahlen ist nicht ratsam, da die Berechnungen, besonders die Prüfung der geeigneten Schlüsselzahl, zu viel Zeit in Anspruch nehmen dürften.
Besser ist es, bei den anfangs gemachten Angaben zu bleiben und mit diesen Parametern ein Quadrat zu bilden.
Dazu bittet Mag um eine 3-stellige Zahl aus dem oberen Bereich. Die genannte Zahl 625 schreibt er über das Quadrat.
Dann lässt er sich eine 2-stellige Zahl nennen, die er in die Zelle 1 einsetzt.
Eine 3. Zahl soll eine 3-stellige sein, die mit einer 1 beginnt. Die genannte Zahl 176 setzt er in die Zelle 8 ein.
Damit ist das Startquadrat fertig. (Siehe Quadrat 2)
Danach trägt er in die übrigen leeren Zellen Zahlen ein, bis das Quadrat fertig ist.
Es ist das Quadrat 3. Es ist ein magisches Quadrat. Die Summe aller Zeilen, Spalten und Diagonalen haben die vorgegebene magische Summe 625.
Jede Zahl ist nur einmal vorhanden.
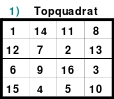
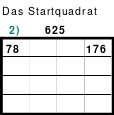
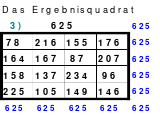
Mag war es gelungen, unter Beachtung der beiden Vorgaben 78 und 176, die richtigen Zahlen zu finden und so in die übrigen Zellen des Quadrates einzuordnen, dass ein magisches Quadrat mit einer magischen Summe von 625 entstand, was der Vorgabe entspricht.
Die Lösung
Die Lösung ist einfach, aber man muss erstmal draufkommen!
Die Grundgedanken dazu sind (immer bezogen auf das Topquadrat):
Die magische Summe wird vorgegeben und damit auch die Duosummen, die ja die Hälfte der magischen Summe sind.
Die Zahlenvorgaben werden als Duozahlen von 2 Duos betrachtet. Die zum jeweiligen Duopaar gehörende 2. Zahl ist dann die Duosumme abzüglich der vorgegebenen 1. Zahl.
Wichtig ist zu wissen, dass die Duozahlen eines Duos immer unterschiedlichen Blöcken angehören. Dabei befinden sich die Duozahlenpaare im 1. und 4. oder 2. und 3. Block. Wird z. B. im 1. Block die erste Zahl 1 gewählt, so ist die 2. Duozahl, die 16, im 4. Block (1+16 = 17). Im Beispiel wurden die 1. Zelle des 1. Blockes (Zelle 1) und die 4. Zelle im 2. Block (Zelle 8) für die Aufnahme der Zahlenvorgaben bestimmt. Es können auch andere 1. Zahlen eines Blockes sein, z. B. 5, 9 oder13 sein. Die 2. Zahl kann dann in die 2 Zellen der in Fragen kommenden Blöcke eingesetzt werden. So kann bei Wahl der Zelle 5 für die 1. Zahl, die 2. Zahl nur in eine 4. Zelle der Blöcke 1 oder 4 eingesetzt werden.
(Andere Festlegungen sind auch möglich, können aber die Berechnungen erheblich erschweren.)
Die Begründung der Wahl des Einsatzes der 2. Zahl in eine 4. Zelle eines möglichen Blockes ist, dass von einer garantiert 3-stelligen Zahl (101 bis 199) immer das 3-fache der Schlüsselzahl 33 oder kleiner abgezogen werden kann. Bei einer magischen Summe 412 und einer 2. Zahl 189 würde die 2. Duozahl 412/2-189 =17 sein, von der nicht das 3-fache der bevorzugten Schlüsselzahlen 7 und 9 abgezogen werden kann.
Die ersten Berechnungen können vorgenommen werden.
Die magische Summe wird durch 2 dividiert und ergibt die Summe der Duos mit 625/2 = 312 und einen Rest 1.
Als nächstes werden die Partnerzahlen der Duos ermittelt. Das ist:
312-78 = 234, die in Zelle 16 einzusetzen ist und
312-176 = 136 die in Zelle 9 eingetragen werden könnte.
Vorher wird aber der Rest 1 zugerechnet und ergibt 137 für die Zelle 9. Da in der Folge jeder Block gesondert berechnet wird hat sich die Einordnung des Restes bereits erledigt.
Es ist folgende Situation erreicht:
In der Zelle 1 ist eine Zahl, die 3-mal um die Schlüsselzahl erhöht werden muss, um die restlichen Zahlen des Blockes, für die Zellen 2, 3 und 4 zu erhalten.
Gleiches gilt für die Zahl in Zelle 9 für die Zellen 10, 11 und 12.
Anders ist die Situation bei den Zahlen in den Zellen 8 und 16, Hier muss 3-mal die Schlüsselzahl abgezogen werden um die anderen Zahlen für die restlichen Zellen der Blöcke zu erhalten.
Es muss nur noch die Schlüsselzahl bestimmt werden, um die Berechnungen der übrigen Zahlen vornehmen zu können.
Mag hat sich für die 9 als Schlüsselzahl entschieden.
Wenn doppelte Zahlen verhindert werden sollen, dann muss noch eine Prüfung erfolgen, ob diese geeignet ist.
Es dürfen die Differenzen zwischen den 4 Duozahlen nicht durch die Schlüsselzahl teilbar sein, aber nur wenn die Differenzen kleiner als das 6-fache der Schlüsselzahl +1 sind. Bei der Schlüsselzahl 9 ist das 6*9+1 = 55. Damit scheiden die Duozahlen 78 und 234 schon mal aus. Die Differenz zwischen den Duozahlen 137 und 176 ist mit 39 zwar kleiner als 54, aber sie ist nicht durch 9 teilbar. Die 9 kann als Schlüsselzahl zum Einsatz kommen und die Berechnungen können beginnen.
(Die Differenz =>55 rd. 60, ergibt sich daraus, dass von den Duozahlen einmal bis zu 3-mal die Schlüsselzahl abgezogen und zum anderen addiert werden muss, was aber nur für Schlüsselzahlen =<9 gilt Bei der Schlüsselzahl 9 ist das 6*9=54. Die 1 sichert, dass die Differenz zwischen den so berechneten Zahlen mindestens 1 ist.
Ist die 9 als Schlüsselzahl nicht geeignet, muss eine andere gewählt werden. Allerdings muss dann die Prüfung evtl. wiederholt werden.)
Nun werden die Zahlen für die restlichen, leeren Zellen ermittele:
Die 78 in Zelle 1 ist die 1. Zahl in einer aufsteigenden Zahlenreihe.
Deshalb wird gerechnet: 78+9 = 87 für Zelle 2, +9 = 96 für Zelle 3,
+9 = 105 für Zelle 4 und schon ist der 1. Block fertig.
Weiter mit 137 in Zelle 9: 137+9 = 146 für Zelle 10, +9 = 155 für Zelle 11,
+9 = 164 für Zelle 12 und der 3. Block ist fertig.
Es folgen die absteigenden Zahlenreihen.
Ab 176 in Zelle 8: 176-9 = 167 für Zelle 7, -9 = 167 für Zelle 6,
-9 = 158 für Zelle 5. Auch Block 2 ist fertig.
Ab 234 in Zelle 16: 234-9 = 225 für Zelle 15, -9 = 216 für Zelle 14 und
-9 = 207 für Zelle 13 und das Quadrat ist komplett.
Das Ergebnisquadrat (3) sieht recht attraktiv aus. Es ist nicht mehr pandiagonal weil keine gleichen Abstände zwischen den Blöcken durch die unterschiedlichen Vorgaben bestehen können.
Deshalb ist es auch nicht möglich, die 1. Zahl in eine vom Zuschauer bestimmte Zelle einzusetzen, was ohnehin zu erschwerten Berechnungen führen würde und deshalb auch darauf verzichtet werden kann.
Da alle Zahlen in den Blöcken mit der gleichen Schlüsselzahl 9 berechnet wurden, ist das Quadrat auch magisch geblieben.
Eine Nachbetrachtung
Mag hat die Aussage getroffen, dass es nicht möglich ist, die Vorgaben in vom Publikum bestimmte Zellen einzutragen.
Diese Angabe ist nicht ganz richtig. Es ist unter bestimmten Bedingungen doch möglich, wodurch die 3-fachen Vorgaben zur 4-fachen und sogar 5-fachen Vorgabe aufgestockt werden können, wenn beide Zahlenvorgaben in gewählte Zellen eingesetzt werden sollen.
Mag hat diese Möglichkeiten in seinen Beschreibungen ausgeklammert, um diese verständlicher zu halten.
Er wird nun die ausgeklammerten Beschreibungen als erweiterte Variante nachholen.
Um die Veränderungen besser zu erkennen, werden dazu die gleichen Vorgaben wie in der ersten Variante eingesetzt.
Ein Möglicher Ablauf der Darbietung.
Die abgefragte magische Summe 625 hat Mag über das Quadrat geschrieben.
Jetzt bittet er um eine 2-stellige Zahl. Es wird 78 genannt. Er fragt, in welche Zelle die 78 eingesetzt werden soll. Es wird die 1. Zelle in der 3. Zeile genannt, in die Mag die 78 einträgt. Als Weiteres bittet er um eine 3-stellige Zahl. Die 176 wird angegeben. Mag bittet einen weiteren Zuschauer “Halt!” zu rufen, wenn er der Meinung ist, dass die 176 dort eingesetzt werden soll. Sofort beginnt er in ungeordneter Reihenfolge auf Zellen zu tippen. Wenn der Zuschauer sein “Halt!” gerufen hat trägt Mag in die so gewählte Zelle die 176 ein.
Der erreichte Zwischenstand zeigt das Quadrat 2, das Mag als Startquadrat bezeichnet.
Danach trägt er in die noch leeren Zellen Zahlen ein, bis das Quadrat fertig ist. Es ist das Ergebnisquadrat 3).
Das Quadrat ist magisch, alle Reihen haben die vorgegebene magische Summe 625 und keine Zahl ist doppelt vorhanden.
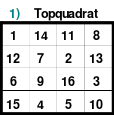
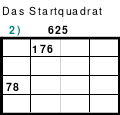
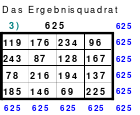
Die Erklärung
Nochmals eine Beschreibung der Einordnung der Duozahlen. Diese Kenntnisse sind sehr wichtig, denn die beiden Zahlen eines Duos befinden sich entweder in den inneren oder in den äußeren Blöcken.
Wurde eine der inneren Zellen für die Eintragung der 2-stelligen Zahl bestimmt, so darf die 3-stellige Vorgabe nur noch in eine Zelle der äußeren Blöcke eingesetzt werden.
Deshalb kann die Zelle für die 3-stellige Vorgabe nicht ganz frei gewählt werden. Im Beispiel wurde die für die 2-stellige Vorgabe die Zelle 6 gewählt. Diese ist eine der inneren Blöcke. Die 3-stellige Vorgabe darf deshalb nicht in eine weitere Zelle der inneren Blöcke eingesetzt werden. Das sind die Zellen 5 bis 12. Jetzt verstehen Sie auch, warum Mag nacheinander auf die zu wählende Zelle getippt hat. Er hat nur auf Zellen des 1. und 4. Blocks getippt und so gesichert, dass die 3-stellige Vorgabe in eine Zelle der äußeren Blöcke kommt. Im Beispiel war es die Zelle 14 bei der “Stopp!” gerufen wurde. Das ist eine Zelle des 4., also äußeren Blocks.
Die zweite, erweiterte Variante, ist an Bedingungen gebunden.
Die Vorgabe für die magische Summe muss =>460 sein. Denn dann wird die Duosumme 230 groß und nach Abzug einer 3-stelligen Vorgabe von maximal 199 (rd. 200) ein Rest von mindestens 30 verbleiben. Von dieser kann das bis 3-fache der Schlüsselzahl 9 oder 7 abgezogen werden. Das kann erforderlich werden, wenn eine der 4 Duozahlen in eine der 4ten Zelle der Blöcke (das sind die Zellen 4, 8, 12 und 16) kommt, was Sie aufgrund der freien Wahl der Zellen nicht beeinflussen können.
Ist die Vorgabe der magischen Summe kleiner, so kann zur Sicherheit nur die einfache Variante vorgeführt werden.
Gleiches gilt auch für die 2-stellige Vorgabe, die mindestens 30 groß muss.
Es ist zwingend, dass nach der Vorgabe der magischen Summe, die Vorgabe der 2-stelligen erfragt werden muss. Dann können Sie nämlich entscheiden ob es bei der erweiterten, die2. Variante bleiben kann.
Erst zuletzt wird die 3-stellige Vorgabe abgefragt, die dann “frei” in eine “manipulierte” Zelle kommt.
Die Berechnung der übrigen Zahlen erfolgt wie beider 1. Variante.
Die Duosumme ist die Hälfte der magischen Summe, wobei ein Rest von 1 übrigbleiben kann. Das ist 625/2 = 312, Rest 1.
Die zweiten Duozahlen werden wie bekannt, durch Abzug der ersten Duozahl von der Duosumme, berechnet. Der Rest wird dabei einer der zweiten Duozahl zugeschlagen. Diese werden 312-78 = 234, die 2 Zellen diagonal weiter in Zelle 11 kommt und 312-176+Rest 1 = 137 für Zelle 3.
Bei der Berechnung der übrigen Zahlen tritt gegenüber der 1. Variante eine leichte Veränderung ein. Was bleibt ist, dass sich in jedem Block eine der 4 Duozahlen befindet, von der aus der Berechnung der übrigen Zahlen für den jeweiligen Block erfolgt kann.
Beginnen wir mit der Zahl 176 in der Zelle 14. Zu diesem Block gehören die Zellen (Zahlen) 13, 14, 15 und 16. Die Zelle 13 ist um 1 kleiner als Zelle 14, weshalb 176-9 =167 in die Zelle 13 eingetragen wird. In die Zell 15 kommt 176+9 = 185 und in Zelle 16 185+9 = 194. Der 4. Block ist fertig.
Die nächsten Zahl 234 befindet sich in der Zelle 11, zu der noch die Zahlen (Zellen) 9, 10 und 12 gehören. In die Zelle 10 kommt 234-9 = 225, in Zelle 9 225-9 = 216 und in die Zelle 12 234+9 = 243. Der 3. Block ist ebenfalls fertig.
In der gleichen Weise werden auch die Zahlen für die Blöcke 2 und 1 berechnet.
Ausgehend von der Zahl 78 in Zelle 6 (Block 2) sind das für Zelle 5 = 69, Zelle 7 = 87 und Zelle 8 = 96. In die Zelle 4 (Block 1) kommt 137+9 = 146, in Zelle 2 137-9 = 128 und in die Zelle 1 128-9 = 119.
Das magische Quadrat mit der magischen Summe 625 fertig! (Quadrat 3)
Noch schwerer, aber möglich, ist das Eintragen der Zahlen nach der “Hohen Schule”. Mag verzichtet darauf, denn die als erste notwendige Berechnung und Eintragung der zweiten Duozahlen steht dazu im Widerspruch.
Der Teufel steckt im Detail
So auch im Hexenquadrat, egal ob 1, oder 2. Variante, was an einem Beispiel nach Variante 1 gezeigt wird.
Die Vorgaben: Magische Summe = 512 und die Zahlen 61 und 195 liegen im Rahmen der Forderungen. Auch die Eintragungen in die Zellen 1 und 8 sind zulässig.
Die Berechnung kann erfolgen.
Nach dem Mag die Duosumme mit 512/2 = 256 errechnet hatte ging er an die Berechnung der zweiten Duozahlen.
Erschrocken stellt er fest, dass die zweiten Duozahlen mit 61 und 195 genau der Vorgaben entsprechen.
Damit kann kein Quadrat gebildet werden. Es würde zwar ein magisches sein, aber alle Zahlen sind dann doppelt, wie es Quadrat 2 zeigt.
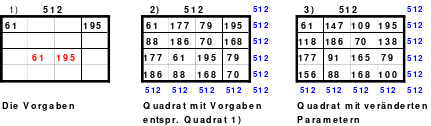
Wie konnte das passieren???
Die Ursache ist, dass die Summe der beiden Vorgaben mit 61+195 = 256, genau dieselbe ist, die Mag aus der magischen Summe mit 512/2 = 256 berechnet hat.
Ein solcher Zufall wird sehr selten auftreten, aber er kann!
Was ist zu tun???
Die Zuschauer bitten, eine der 3 Vorgaben zu verändern, muss abgelehnt werden, denn es zeigt, dass der “Rechenkünstler” doch nicht so gut ist, wie es scheinen soll.
Auch wenn Mag annehmen kann, dass Sie es wissen, erklärt er was zu tun ist.
Aus den bisherigen Erläuterungen ist bekannt, dass in einem unveränderten Topquadrates, in jeder Zeile, Spalte und in den Diagonalen je eine Zahl aus den 4 Blöcken enthalten ist. Daraus ist abzuleiten, dass das Quadrat magisch bleibt, wenn die 4 Zahlen eines Blockes um eine einheitliche Zahl erhöht oder verringert wird.
Diese Regel nutzt Mag, in dem er die Zahlen eines Blockes um eine Größe erhöht und in einen anderen, zum Ausgleich, um die gleiche Größe vermindert.
Als Mag erkannte, dass nach Abzug der 61 von 256 die Zahl 195 entsteht, die einer Vorgabe entspricht, zog er 30 von dieser ab und erhielt 165, die er in die Zelle 16 einsetzte.
Zum Ausgleich erhöhte er dann die zu berechnende zweite Duozahl 61 um 30 und setzte die so ermittelte Zahl 91 in die Zelle 9 ein.
Damit war das scheinbare Problem aus der Welt.
Mag schließt seine Ausführungen mit den am Anfang der Erläuterungen zitierten Satz:
”Die Lösung ist einfach, aber man muss erstmal drauf kommen!”
Mag hat die Beschreibungen sehr detailliert vorgenommen. Er betrachtet das als erforderlich, denn dieses Experiment ist trotz der Einfachheit sehr ansprechend und findet sicherlich bei manchem Fan Anwendung.
Das Schwerste, aber auch leichtes, ist das Rechnen mit 3-stelligen Zahlen, weshalb Mag dieser Routinen auch einen Stern zuerkannt hat.
Aber auch hier sind weitere Vereinfachungen der Berechnung, z. B. durch einen “manipulierten Rest“ möglich. So kann z. B. die Vorgabe der magischen Summe von 625 gedanklich auf 600 verändert werden. Diese ist leicht durch 2 teilbar (600/2=300). Auch können die Vorgaben von 300 leichter abgezogen werden. Die abgezogenen 25 werden dann wie beschreiben als Rest einer der berechneten zweiten Duozahlen zugerechnet. Nicht immer kann die vorgegebene magische Summe gedanklich auf eine Hunderterzahl reduziert werden. Es muss immer operativ entschieden werden. So wären z. B. möglich: MS=657 = 640, Rest +17, oder 782 = 800, Rest -18.
Auch kann darüber nachgedacht werden, welcher der 2 berechneten Duozahlen der Rest sinnvoll zugeordnet werden sollte.
Dieser kleine Ausflug in das operative Rechnen soll zeigen, dass es sinnvoll ist, sich über die Berechnungen weitere Gedanken zu deren Vereinfachung zu machen.
6.3.5. Die glorreichen 4 (4-fach-Vorgaben) im Zentrum
Auf der Tafel ist ein Quadrat der 4. Ordnung aufgezeichnet. Mag bittet einen oder auch mehrere Zuschauer in das mittlere 2 mal 2 große Teilquadrat 4 beliebige, größere, 2-stellige Zahlen einzusetzen. Im Beispiel sind es die Zahlen 67, 85, 77 und 82. Das linke Quadrat zeigt diese Eintragungen.
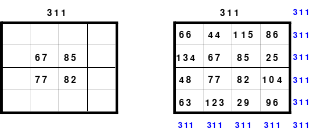
Mag übernimmt die Kreide und schreibt über das Quadrat die Zahl 311. Anschließend schreibt er in die leeren Zellen zeilenweise, entsprechend der hohen Schule, Zahlen. Nach Fertigstellung erklärt Mag den Zuschauern, dass das so entstandene Quadrat ein magisches, mit der magischen Summe von 311 ist. Die Jury kann nach Überprüfung diese Aussage bestätigen. Das fertige Quadrat ist das rechte.
Mag ist es gelungen, die vorgegebenen Zahlen so in seine Berechnungen einzubinden, dass zum Schluss ein magisches Quadrat entstanden ist, deren magische Summe er vorher über das Quadrat geschrieben hatte. Eine ansprechende Leistung, oder nicht?
Ansprechend schon, aber nicht schwierig!
Die Lösung
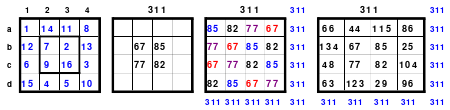
Das linke Quadrat ist das gut bekannte Topquadrat. Die mittleren 4 Zahlen 7, 2, 9 und 16 bilden ein als Quattro bezeichnetes Quadrat aus 2 mal 2 Zellen, das bekanntermaßen nie ein magisches sein kann. Analysieren wir nun das Quattro. Es enthält die Zahlen:
9, die 1. Zahl im 3. Block, 2, die 2. Zahl im 1. Block
7, die 3. Zahl im 2. Block und 16, die 4. Zahl im 4. Block.
Es ist im Quattro von jedem Block eine Zahl vorhanden. Weiter sind es eine 1., 2., 3. und 4. Zahlen des jeweiligen Blockes. Somit ist das Quattro homogen und die 4 Zahlen ergeben die magische Summe 34. Diesen Umstand nutzt Mag bei der Bestimmung der magischen Summe, indem er die 4 Zahlen des Zuschauers addiert. Wer nicht schnell genug die 4 Zahlen addieren kann, sollte zwei oder noch mehr Zuschauer bitten eine Zahl einzusetzen. So gewinnt er durch den Wechsel Zeit. Des Weiteren wird die Annahme ausgeschlossen, dass der Vorführende mit bestellten Personen arbeitet.
Theoretisch könnte Mag nun in alle Blöcke die gleichen Zahlen eintragen, die die Zahl des entsprechenden Blockes ist. Siehe 3. Quadrat. Das wäre in den 1. Block die 85 (blau), in den 2. Block 67 (rot) usw. Damit will Mag nur daran erinnern, dass es fast gleichgültig ist, wie groß die Differenz zwischen den Zahlen eines Blockes ist. Die Differenz muss nur im gesamten Quadrat verwendet werden. Die Differenz, oft als Schlüsselzahl bezeichnet, muss jedoch so klein sein, dass beim Subtrahieren keine negativen Zahlen entstehen. Dabei ist es gleichgültig wie groß die einzelnen Differenzen zwischen den Blöcken ist, was natürlich nur für dieses Rechenexperiment gilt, da das Quadrat nicht verändert wird.
Das mit den gleichen Zahlen kann natürlich nicht so dem Zuschauer präsentiert werden. Es zeigt aber, dass die Schlüsselzahl nahezu frei gewählt werden könnte und sogar Null sein kann. Nahezu heißt, sie darf nicht zu groß sein, dass negative Zahlen entstehen. Andererseits sollte sie nicht zu klein sein, weil dann keine breite Streuung der Zahlen erreicht wird. Die Schlüsselzahl sollte auch ein leichtes Rechnen ermöglichen und nicht so leicht erkennbar sein. Mag bevorzugt deshalb Schlüsselzahlen die er grob ermittelt und mit der 9 als letzte Ziffer.
Doch nun weiter bei der Erstellung des magischen Quadrates.
Als nächstes muss die Schlüsselzahl ermittelt werden. Die Zahl 67 ist die 3. Zahl im Block 2. Von dieser muss die 2-fache Schlüsselzahl abgezogen werden, um die Zahl für die Zelle 3d, die 5, zu erhalten. Folglich wird die 6 durch 2 geteilt und erhält 30 als mögliche Schlüsselzahl. Die weitere Prüfung zeigt, dass diese zu groß ist. Denn von der Vorgabe 82 in Zelle 3c (16) muss die Schlüsselzahl 3-fach abgezogen werden um die Zahl 13 in Zelle 4b zu erhalten. 8/3=2, folglich 20 als Schlüsselzahl und gewählt 19, das ist auch 20-1.
Für Anfänger schlägt Mag eine leichtere Variante vor:
Es bleibt bei 2-stelligen Vorgaben, allerdings ohne eine Beschränkung.
Es werden nur 1-stellige Schlüsselzahlen eingesetzt, bevorzugt 7, 9 und im Ausnahmefall auch kleinere, bis zur 3, die aber kaum gewählt werden muss.
Der Grund für diese Festlegungen ist eine einfachere Prüfung welche Schlüsselzahl anzuwenden ist. Maximal wird die Schlüsselzahl 3-mal von den Vorgaben abgezogen. Das bedeutet, dass die kleinste Zahl das 3-fache+1 der Schlüsselzahl sein kann. Plus 1 sichert, dass nach Abzug des 3-fachen der Schlüsselzahl noch 1 übrigbleibt. Das erfordert z. B. bei der kleinsten 2-stelligen Zahl 10 die Schlüsselzahl 3. Denn 3*3+1 = 10. Ist die kleinste Zahl größer 27, so kann jede 1-stellige Schlüsselzahl eingesetzt werden. Es wird keine Null oder negative Zahl bei den Berechnungen auftreten. Denn 9*3+1 = 28.
Dazu dividieren Sie die kleinste Zahl durch 3, und die Schlüsselzahl ist gefunden. Sie muss mindestens um 1 kleiner als das Ergebnis sein.
Beispiel: Die kleinste Vorgabe ist 24. 24/3 = 8, die gewählte Schlüsselzahl kann 7, oder kleiner sein.
Gerade Schlüsselzahlen sollten nicht gewählt werden, wenn die Vorgaben nur gerade oder ungerade Endziffern haben, weil dann alle Endziffern im Quadrat gerade oder ungerade werden, was allerdings auch unbeachtet werden kann.
Nachfolgende Quadrate mit den gleichen Vorgaben, jedoch mit unterschiedlichen Schlüsselzahlen.
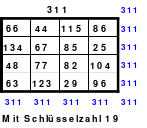
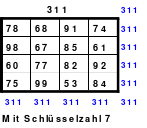
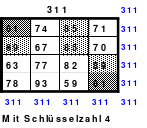
Das linke Quadrat ist das zuerst gezeigte mit der Schlüsselzahl 19.
In der Mitte ein Quadrat mit der Schlüsselzahl 7. Die Zahlen sind deutlich weniger gestreut, jedoch noch vorzeigbar.
Das rechte mit der Schlüsselzahl 4 ist zwar auch noch ansehnlich, jedoch sind hier gleich 3 Zahlen doppelt. Der Grund sind die Vorgaben 77 und 85. Die Differenz zwischen diesen Zahlen ist 8 und 8 ist eine durch die Schlüsselzahl 4 teilbare Zahl.
Ebenfalls doppelte Zahlen würden entstehen bei der Schlüsselzahl 3 wegen der Vorgaben 82 und 85, bei der Schlüsselzahl 5 wegen 67 und 77 auch 77 und 82.
Die Gründe sind die kleinen Schlüsselzahlen in Verbindung mit den geringen Differenzen zwischen den Vorgaben. Die Differenzen zwischen den Vorgaben können Sie nicht beeinflussen, aber die Schlüsselzahlen schon, vorausgesetzt die Vorgaben sind groß genug.
Wegen dieser Mängel sollte diese Variante wirklich nur am Anfang angewendet werden.
Doch nun weiter mit der Berechnung der Zahlen für die offenen Zellen.
In der Zelle 1a ist im Basisquadrat die Zahl 1 des 1. Blockes. Die Zahl des 1. Blockes im Quattro ist die 2. Folglich muss von dieser 1-mal die Schlüsselzahl von 85 abgezogen werden. 8-2=6 und 5+1=6, Zusammen 66. Die nächste Zahl im Basisquadrat ist die 14. Hier muss von 82 in Zelle 3c, 2-mal die Schlüsselzahl abgezogen werden. Das ist 8-2*2=4, und 2+2*1=4, zusammen 44. Die 11 in Zelle 3a ist die 3. Zahl im Block 3. Im Quattro ist als 1. Zahl des 3. Blockes die 77 in Zelle 2c, die Zelle mit der 9 im Basisquadrat, eingetragen. Folglich muss die 77 um 2-mal die Schlüsselzahl erhöht werden. Das ist 77+38, oder wieder vereinfacht, 7+2*2=11 und 7-2*1=5, zusammengefügt 115. So werden nacheinander alle offenen Zellen berechnet. Am Ende ist das rechte Quadrat das Ergebnis. Ein magisches Quadrat mit der magischen Summe von 311.
Mag hofft, Sie von der Leichtigkeit der Lösung überzeugt zu haben.
Ein Nachteil besteht darin, dass es zu doppelten Zahlen kommen kann. Hätte der Zuschauer z. B. in die Zelle 2b statt der 67 die Zahl 66 eingesetzt, würde für Zelle 8 die Zahl 66+19 = 85 sein. Das wäre dann die gleiche Zahl des Zuschauers in Zelle 3b.
Die Gefahr des Entstehens doppelter Zahlen muss in Kauf genommen werden. Nur müssen Sie dann auf die Aussage “und keine Zahl ist doppelt!” verzichten.
Um doppelte Zahlen zu verhindern, müssten alle Differenzen zwischen den Vorgaben berechnet und deren Teilbarkeit durch die Schlüsselzahl geprüft werden. Das wären 6 Einzelberechnungen, die eine zu große Zeitspanne erfordern würde. Nach Wahl einer veränderten Schlüsselzahl müsste die gesamte Kontrollberechnung wiederholt werden.
Eine bessere Variante ist die Vorgabe von nur 2 Zahlen, die nur eine Kontrollrechnung erfordert. Dazu sind die Ausführungen von Mag zum Experiment “Das Quattroquadrat” analog anzuwenden.
Das Quadrat ist nicht pandiagonal, weil die Abstände zwischen den einzelnen Blöcken nicht gleich groß sind.
Zum Schluss noch eine Nachbetrachtung.
In dieser Form können selbstverständlich auch größere Zahlen, z. B. 3- oder 4-stellige zum Einsatz kommen. Mag empfiehlt jedoch keine 4-stelligen oder noch größere Zahlen zu verwenden. Das hat mehrere Gründe. So wird das Rechnen mit größeren Zahlen schwieriger, denn es müssen auch größere Schlüsselzahlen zum Einsatz kommen. Kleine Schlüsselzahlen wie die 19 bringen dann keine große Streuung der Zahlen und die einzelnen Blöcke werden regelrecht sichtbar. Fehler können sich leichter einschleichen.
Ein schwerwiegenderer Grund ist, dass das Interesse der Zuschauer größer ist, wenn sie den Darbietungen folgen können und auch mal selbst etwas kontrollieren können. Beim Einsatz zu großem Zahlen ist das Interesse geringer. Man lässt das Ganze mehr oder weniger über sich ergehen. Man kann Ihnen glauben was Sie sagen, oder auch nicht.
Andererseits ist die Entstehung doppelter Zahlen geringer, je größer die Vorgaben sind, weshalb nach der Einarbeitung 3-stelligen Vorgaben der Vorzug zu geben ist.
Eine Erhöhung des Showeffekts kann erreicht werden, indem die Zuschauer eine freie Zelle wählen können, mit der die Fertigstellung des Quadrates begonnen werden soll. Auch ist die Eintragung der Zahlen im Uhrzeigersinn vorteilhafter.
Das Quartett
Wie bei “Im Zentrum” bittet Mag um vier 2-tellige Zahlen, die jetzt in die Eckzellen eingesetzt werden sollen. Es sind die Zahlen 43, 26, 17 und 51. Sofort schreibt Mag über das Quadrat die Zahl 137. (Quadrat oben Mitte), Anschließend schreibt er in das Quattro oben links weitere 3 Zahlen ein und erklärt, dass die 4 Zahlen als Summe 137, wie vorher angeschrieben, haben. Mag bittet die Zuschauer ihre Smartphons zur Hand zu nehmen und mittels der Rechner-App diese Aussage zu kontrollieren.
Dann folgt das Quattro unten rechts, danach das Quattro unten links und zum Schluss das Quattro oben rechts.
(Die Reihenfolge kann frei gewählt werden.)
Nach jedem fertig gestellten Quattro weist er darauf hin, dass die Summe der jeweils 4 Zahlen, der Zahl über dem Quadrat entspricht,
(Die unten dargestellten Quadrate zeigen die einzelnen Schritte der Quadratbildung.)
Zum Schluss erklärt er, dass auch das in der Mitte befindliche Quattro die Summe 137 hat und nach einer kleinen Kunstpause verkündet er, praktisch als Höhepunkt, dass das gesamte 4 mal 4 große Quadrat ein magisches ist, in dem die Summen aller Zeilen, Spalten und der beiden Diagonalen ebenfalls die magische Summe von 137 haben.
Mag hat es geschafft, unter Beachtung der 4 Vorgaben ein magisches Quadrat zu erstellen, bei dem alle 2 mal 2 großen Quattros die gleiche Summe haben wie sie Mag anfangs über das Quadrat geschrieben hatte, was auch auf die Zeilen, Spalten und Diagonalen zutrifft. Eine beachtliche und interessante Leistung.
(Oder etwa nicht?)
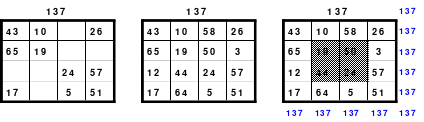
Die Lösung
Eine Beschreibung der Lösung ist eigentlich nicht notwendig, wenn die vorangegangenen Beiträge richtig ausgewertet wurden.
Wie bei “Im Zentrum” wurden die 4 Vorgaben addiert und als magische Summe über das Quadrat geschrieben.
Die Prüfung ergab, dass die 9 als Schlüsselzahl nicht zum Einsatz kommen kann. So kann von der 26 in Zelle 8 nicht 3*9 = 27 abgezogen werden, um zu der Zahl für die Zelle 5 zu kommen. Auch die Berechnung der Zahl für Zelle 13 ist nicht möglich. Hier müsste 2*9 = 18 von der 17 in Zelle 15 abgezogen werden. Mag entschied sich deshalb für die Schlüsselzahl 7.
Die Berechnungen der Quattros erfolgen analog der Berechnungen wie in “Im Zentrum” für den zeilenweisen Eintrag beschrieben. Das wird für das Quattro oben links erläutert. Dazu ist das Topquadrat oben links, welches auswendig beherrscht werden muss, zu beachten.
Neben der Zelle 1 befindet sich die Zelle 14. Die Zahl für Zelle 14 wird durch Abzug von 1*7 = 7 von der Zahl 17 in Zelle 15, das ist 17-7 = 10 berechnet.
Unter der Zelle 1 ist die Zelle 12, die letzte Zahl im 3. Block. Und das bedeutet, dass die 51 als 2. Zahl im 3. Block um 2*7 = 14 auf 65 erhöht werden muss.
Die letzte Zahl im Quattro ist die Zahl für Zelle 7. Da 7 um 1 kleiner als 8 ist, wird von der 26 in Zelle 8 folglich 1*7 = 7 abgezogen und man erhält 19 als Zahl für Zelle 7.
So werden bis zur Fertigstellung es Gesamtquadrates die weiteren Quattros berechnet.
Das Quadrat ist jedoch, wie auch “Im Zentrum”, nicht pandiagonal.
Doppelte Zahlen sind auch hier möglich. Es gelten auch hier die im Beitrag “Im Zentrum” dazu gemachten Erläuterungen, was auch für den Einsatz großer Zahlen gilt.
Mag hat hier eine Lösung auf der Basis der Multimethode beschrieben. Den gleichen Effekt hat er bereits im Experiment “Das Quattroquadrat”, unter 3. Doppelvorgaben, erreicht und das ohne Gefahr von doppelten Zahlen. Damit wird die Überlegenheit der Duomethode unterstrichen.
6.3.6. Einfach clever
Das Rechenexperiment “Einfach clever” zählt zu den von Mag bevorzugten. Es ist im wahrsten Sinne des Wortes einfach clever, einfach in der Berechnung und clever ist die Idee. Dieses Experiment wird bestimmt Ihre Anerkennung finden, wenn Sie sich mit der einfachen Lösung vertraut gemacht haben.
Hervorgehoben werden muss, dass diese Methode auch mit geringen Abweichungen für die Bildung von Quadraten der 5. und 7. Ordnung Anwendung finden kann.
Allerdings können je nach Vorgabe Mängel auftreten. Diese können allgemein vernachlässigt werden, jedoch nicht, wenn man 100%ige Qualität erreichen will, oder erreichen muss, was z. B. auf Profis zutrifft. Mag wird Wege zur Vermeidung von diesen Mängeln aufzeigen.
Aber zuerst ein Beispiel.
Eine Zahlenvorgabe
Auf der Tafel ist ein leeres Quadrat der 4. Ordnung aufgezeichnet.
Mag bittet um die Nennung einer größeren 2-stelligen Zahl. Es wird 54 genannt, die Mag in die erste Zelle einträgt.
Sofort schreibt er über das Quadrat die Zahl 168. (linkes Quadrat)
Anschließend trägt er in die leeren Zellen zeilenweise, wie in der “Hohen Schule”, unterschiedliche Zahlen ein.
Nach Fertigstellung erklärt Mag, dass das erstellte Quadrat ein magisches ist, mit der magischen Summe von 168 und keine Zahl doppelt vorkommt. (rechtes Quadrat)
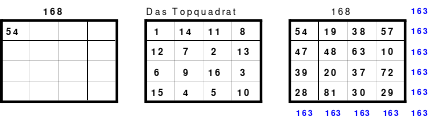
Das Quadrat ist nicht pandiagonal, weil durch die Vorgabe die Übergänge von Block zu Block nicht einheitlich sind. Das bedeutet, dass auch hier auf eine Vorgabe der Zelle, mit der begonnen werden soll, verzichtet werden muss.
Die Lösung
Bevor Mag zum Kern der Erläuterungen kommt, beschreibt er die durchgeführten Berechnungen, um Ihnen zu zeigen, dass diese keinerlei Schwierigkeiten darstellen.
Nach dem die Vorgabe 54 in die Zelle 1 eingesetzt ist, berechnet Mag die magische Summe mit der gewählten Schlüsselzahl 9 wie folgt:
6*9 = 54 + 6*10 = 114 zu der Mag die Vorgabe addiert und erhält 114+54 = 168.
Dann folgen die weiteren Zahlen für die erste Zeile mit:
1*9 = 9 + 1*10 = 19; die nächste Zahl 2*9 = 18 + 2*10 = 38 und die 3. Zahl mit 3*9 = 27 + 3*10 = 57.
Bei den Berechnungen der folgenden Zeilen wird stets von den Zahlen der 1. Zeile das bis zum 3-fachen der Schlüsselzahl 9, das ist 9, 18 und 27, abgezogen oder zugeschlagen.
Und das war es schon!
Wie Mag zu den Zahlen kommt und dass diese sich ganz leicht merken oder berechnen lassen, wird Mag in den folgenden Erläuterungen zu den Details zeigen.
Die Details
Die weiteren Erläuterungen erfolgen unter Beachtung der Tabelle, linker Teil.
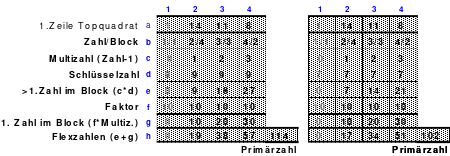
In der Zeile a sind die Zahlen der ersten Zeile des Topquadrates eingesetzt. Das ist 1, 14, 11 und 8. In den weiteren Betrachtungen geht es nur um die Spalten 2 bis 4, weshalb die Spalten 1 auch nur in grau gehalten ist.
In der Zeile b ist dargestellt, die wievielte Zahl in welchem Block diese Zahlen sind. Die 14 ist die 2. Zahl im 4. Block (2/4), die 11 die 3 Zahl im 3. Block (3/3) und die 8 ist die 4. Zahl im 2. Block (4/2).
Geht man nun davon aus, dass die 2. Zahl im Block um 1 größer ist als die 1. Zahl, die 3. Zahl um 2 größer ist usw. so ergeben sich die Multizahlen in Zeile c durch Reduzierung der Zahl im Block um 1. Diese Zahlen sind in der Zeile c abgebildet. Sie bilden die Reihenfolge 1, 2 und 3. und sind leicht zu merken. Auch die Summe der 3 Zahlen, gleich 6, ist gut zu merken, oder notfalls auch zu berechnen.
Werden die Multizahlen mit der Schlüsselzahl multipliziert, so erhält man das Produkt in Zeile e. Das sind die Werte, um wie viel die Zahl größer ist, als die 1. Zahl im Block.
Auch die 1. Zahlen in den Blöcken werden ganz leicht berechnet, in dem der Faktor (Zeile f) mit der Multizahl multipliziert wird.
Der Faktor ist notwendig um keine Nullen für die ersten Zahlen im Block zu erhalten und zum anderen, um doppelte Zahlen in den berechneten Werten der Spalten 2 bis 4 zu verhindern und sollte nicht kleiner 10 sein.
(Ein größerer Faktor kommt nur bei größeren Vorgaben zur Anwendung und wird später beschrieben.)
Die Addition der Zahlen aus Zeile e+g ergeben die Flexzahlen in Zeile h.
Die Flexzahlen berechnen sich folglich ganz leicht, indem die Schlüsselzahl mit der Multizahl multipliziert wird und anschließend das Produkt aus Multizahl mal Faktor zugerechnet wird.
Damit wird die allgemeingültige Formel für die Flexzahlen:
M*S+Fa*M = Fl
Darin sind: M ist die Multizahl; S die Schlüsselzahl; Fa der Faktor und Fl die Flexzahl.
Das ist im Beispiel für die 1. Zahl in Spalte 2, das ist die Zelle 14 im Grundquadrat:
1*9 = 9 + 1*10 = 9+10 = 19
Die nächste Zahl in Zeile 1 wird:
2*9 = 18 +2*10 = 18+20 = 38
und für die letzte Zelle in Zeile 1:
3*9 = 27 +3*10 = 27+30 = 57.
Die Flexzahlen sind durch mögliche Änderung der Schlüsselzahl oder auch des Faktors flexibel.
Die Flexzahlen werden jedoch erst nach Festlegung der magischen Summe eingesetzt. Die Ermittlung der magischen Summe ist ebenfalls einfach.
Die Summe der Flexzahlen ergibt die Primärzahl und kann deshalb wie nachstehend berechnet werden:
Die Summe der Multizahlen ist 1+2+3 = 6.
Die Berechnung der Primärzahl erfolgt in gleicher Weise wie die
Flexzahlen.
Das ist im Beispiel 9*6=54 +10*6=60 zusammen 114.
Um die magische Summe zu erhalten wird nur noch die Vorgabe zu 114 gezählt, das ist im Beispiel 114+54 = 168, die über das Quadrat geschrieben wird.
Anschließend werden die Flexzahlen wie bereits beschrieben errechnet und eingetragen.
Sind die Flexzahlen in die 1. Zeile eingesetzt, werden die Zahlen für die nächsten Zeilen berechnet und eingesetzt.
Voraussetzung dafür ist, dass das Topquadrat bestens beherrscht wird. Als Beispiel die Berechnung der 2. Zeile.
Unter der Zelle 1 befindet sich die Zelle 12. Diese ist die 4. im 3. Block. In der 1. Zeile befindet sich die Zelle 11 ebenfalls eine Zahl des 3. Blockes. Da 12 um 1 größer als 11 ist, wird die Zahl in Zelle 11 um 9 erhöht, das ist 38+9 = 47.
Die nächste Zelle ist die Zelle 7, die zum 2. Block gehört, die um 1 kleiner ist, als Zelle 8, die ebenfalls zum 2. Block gehört, weshalb die Zahl in Zelle 8 um 1 mal 9 reduziert werden muss, das ist 57-9 = 48.
Weiter mit Zelle 2 die um 1 größer als Zelle 1 ist, folglich 54+9 = 63.
Die letzte Zelle in Zeile 2 ist die 13. Diese gehört zum 4. Block. Zum 4. Block gehört auch die Zelle 14, weshalb von der Zahl in Zelle 14, 1 mal 9 abgezogen werden muss, das ist 19-9 = 10.
In dieser Form werden auch die Zeilen 3 und 4 berechnet. Dazu gibt Mag die Empfehlung, sich bei den Berechnungen immer auf die Zahlen in der 1. Zeile zu beziehen und nicht auf die Zahlen der vorangegangenen Zeile. Dadurch kann ein Fehler, der keinesfalls vorkommen sollte, nicht weitergeschleppt werden.
Die größte Zahl, die abgezogen oder zugerechnet werden muss ist bei einer Schlüsselzahl 9 = 27 (3*9).
Alle Berechnungen im Beispiel erfolgten mit der Schlüsselzahl 9. Bei der Wahl einer anderen Schlüsselzahl sind die Berechnungen analog durchzuführen. Dazu als Beispiel die Berechnungen mit der Schlüsselzahl 7, die im rechten Teil der anfangs dargestellten grün schattierten Tabelle zu finden ist.
Eine Nachbetrachtung
Die vorgestellte Lösung ist einfach und damit leicht anzuwenden. Hervorzuheben ist, dass kein Rest anfällt, der ja z. T. schwierig einzugliedern ist.
Diese Methode hat den Vorteil, dass sie auch bei Quadraten der 5. und 7. Ordnung angewendet werden kann. Dabei ist von Bedeutung, dass bei diesen Quadraten der Aufbau nicht erlernt sein muss.
(Siehe dazu Beschreibungen zu den Quadraten der 5. und 7. Ordnung.)
Allerdings können bei den nach dieser Methode gebildeten Quadraten Mängel auftreten, die aber in der Regel vernachlässigt werden können.
Trotzdem wird Mag Möglichkeiten aufzeigen diese zu verhindern, was allerdings auch zu einer Steigerung der zu erbringenden Leistungen nach sich zieht.
Derartige Mängel können sein:
Das Quadrat ist nicht mehr pandiagonal, weil durch die Vorgabe die Übergänge von Block zu Block nicht mehr einheitlich sind. Das bedeutet, dass auf eine Vorgabe der Zelle, mit der begonnen werden soll, verzichtet werden muss.
Es können doppelte Zahlen auftreten, was von der Vorgabe abhängig ist. Ob doppelte Zahlen eventuell auftreten können, kann an der letzten Ziffer der Vorgabe erkannt werden. Kritische Endziffern der Vorgabe können 0; 1; 2 oder 3 sein. Das gilt aber nur für das gezeigte Beispiel mit einer Schlüsselzahl 9 und kann nicht allgemein angewendet werden. Andere Schlüsselzahlen führen zu anderen Endziffern. Da gegebenenfalls auf andere Schlüsselzahlen ausgewichen werden muss, bzw. bei Wiederholungen erforderlich werden, kann diese Regel nicht angewendet werden. Andere Überprüfungen machen umfangreiche Berechnung notwendig, für die keine Zeit zur Verfügung steht.
Eine allgemein gültige Variante ist, dass die Vorgabe größer sein muss als die Zahl in Zelle 8, da diese die größtmögliche Zahl ist, die sich aus den Flexzahlen ergeben kann. Von dieser wird immer nur die Schlüsselzahl abgezogen, während sich aus der Vorgabe keine kleineren Zahlen ergeben können. Denn sie ist die 1. Zahl im 1. Block, die in der weiteren Folge um jeweils die Schlüsselzahl vergrößert wird.
Als Faustzahl für die Vorgabe gilt für das Topquadrat und die Schlüsselzahlen 9 und 7, eine Zahl größer 50. Deshalb hat Mag auch um eine größere 2-stellige Zahl gebeten.
Wer auf diese Begrenzung verzichten will, muss die Flexzahlen verkleinern. Das kann bis zur Flexzahl 12 geschehen, wenn als Schlüsselzahl 3 und als Faktor 1 festgelegt wird. In Zelle 8 kommt dann die Zahl 3*3+3*1=12.
Ein Quadrat mit so kleinen Parametern ist aber als unattraktiv abzulehnen.
Es können auch keine doppelten Zahlen entstehen, wenn die Vorgabe eine ungerade Zahl ist. Dann muss allerdings eine gerade Schlüsselzahl, z. B. 8, gewählt werden und der Faktor muss ebenfalls eine gerade Zahl z. B.10 sein.
Die Zahlenfolge der Flexzahlen bei der Schlüsselzahl 9 ist | 19 | 38 | 57 | und leicht als aufsteigende Zahlenreihe mit der Differenz von 19 zu erkennen. Gleiches trifft mit der Schlüsselzahl mit den Flexzahlen | 17 | 34 | 51 |zu.
Mag betrachtet das als kleinen Schönheitsfehler der nicht beachtet werden sollte.
Wer aber durchaus vollkommen sein will, dem zeigt Mag Möglichkeiten für Veränderungen, wie sie in die folgenden Quadrate als Beispiele eingegangen sind.
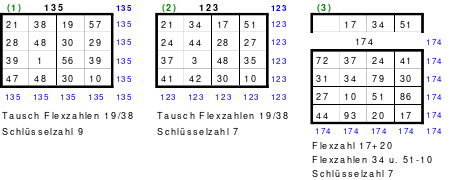
Vorgabe 72
In den Quadraten 1 und 2 wurden die Flexzahlen in den Zellen 14 und 11 getauscht. Voraussetzung ist, dass der Faktor mindestens 10 ist, weil sonst Null oder eine negative Zahl in Zelle 9 entsteht. Die Primärzahl ändert sich dabei nicht.
Auch im Quadrat 3 ändert sich die Primärzahl nicht. Hier wurde ganz einfach die Flexzahl in Zelle 14 um 20 erhöht und als Ausgleich die Flexzahlen in den Zellen 11 und 8 um 10 reduziert. Der Faktor sollte auch hier nicht kleiner 10 sein.
In den Quadraten 4 und 5 wurden, wie in den Quadraten 1 und 2, die Flexzahlen der Zellen 14 und 11 getauscht. Zusätzlich wurden die Flexzahl in Zelle 11 um 9 erhöht. Durch diese Manipulation kann der Faktor fast beliebig, auch mit 1, gewählt werden. Die Primärzahlen erhöhen sich dadurch bei der Schlüsselzahl 9 auf 123 und bei der Schlüsselzahl 7 auf 111. Beide können gut gemerkt werden.
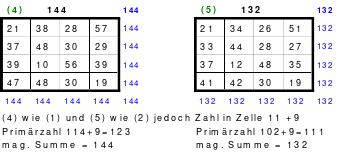
In den bisherigen Beschreibungen und Erklärungen hat Mag diese Möglichkeiten bewusst nicht genutzt, weil es erstmal wichtig war, die Methode zu vermitteln.
Weitere geringe Auffälligkeiten werden als nicht wesentlich ignoriert. Das ist z. B. die Zahlenfolge 47 | 48, die beiden ersten Zahlen in der 2. Zeile. Die Differenz von 1 ist gleich der zwischen Faktor 10 und Schlüsselzahl 9. Diese tritt nicht auf, wenn die Schlüsselzahl, oder der Faktor verändert wird. Das zeigen die beiden Quadrate, bei denen einmal die Schlüsselzahl auf 7 und das andere Mal der Faktor auf 20 verändert wurde, wobei die Vorgabe nicht verändert wurde.
(Mag bevorzugt deshalb in der Regel die Schlüsselzahl 7 und weicht nur wenn erforderlich auf die Schlüsselzahl 9 aus, was nur notwendig wird, wenn bei der Wiederholung der gleiche Faktor zur Anwendung kommt.)
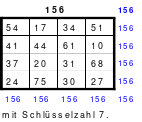
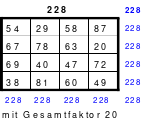
Im rechten Quadrat sind keine doppelten Zahlen vorhanden, obwohl die Vorgabe kleiner ist als 87 in Zelle 8. Das ist begründet in der 4 als letzte Ziffer der Vorgabe.
Beide Quadrate zeigen auch die Möglichkeiten die für Wiederholungen genutzt werden können.
Sie müssen sich entscheiden, ob Sie sich mit den zusätzlichen Regeln belasten wollen, oder bei der Grundvariante bleiben und die Mängel in Kauf nehmen.
Eine 3-stellige Vorgabe
3-stellige Vorgaben und noch größere, werden wie bei den 2-stelligen Vorgaben abgearbeitet, was sich jedoch nur auf die Methode bezieht. Das kann jedoch nicht mit den gleichen Parametern erfolgen, wenn optisch ausgeglichene Quadrate das Ziel sind. Anhand eines Beispiels wird das erläutert.
621 als Vorgabe
Das linke Quadrat wurde mit der Schlüsselzahl 9 und dem Grundfaktor 10, ohne Zusatzfaktor gebildet. Es besteht aus 4 Zahlen größer 600 und 12 Zahlen kleiner 100. Ein ausgewogenes Quadrat sieht anders aus, weshalb solch ein Ergebnis abgelehnt werden muss.
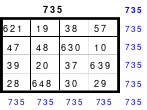
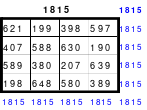
Das rechte Quadrat sieht dagegen viel gefälliger aus. Durch Anpassen der Flexzahlen an die Vorgabe konnte dieses Ergebnis erreicht werden. Wie das erfolgt, wird nachfolgend beschrieben.
Um doppelte Zahlen zu vermeiden muss die größte Flexzahl in Zelle 8 kleiner als die Vorgabe sein.
Die Flexzahl für die Zelle 8 wird wie folgt berechnet: 3*S+3*Fa=F8
Darin bedeuten: S = Schlüsselzahl; Fa = Faktor und F8 = Flexzahl für Zelle 8.
Durch Umstellung erhält man F8-3*S=3*Fa und weiter (F8-3*S) /3=Fa
Für die Flexzahl wird eine Zahl kleiner als die Vorgabe 621 eingesetzt, z. B. 620.
Als Schlüsselzahl wird 9 gewählt.
Damit wird Fa= (620-3*9) /3. Dabei kann 3*9=27 auf 30 aufgerundet werden. (Auch 3*7=21 kann zu 30 aufgerundet werden, wodurch die Berechnung des Gesamtfaktors bei einer Schlüsselzahl 7 in gleicher Weise berechnet werden kann.)
Weiter: (620-30) /3=G, ergibt 590/3=190. (Der Rest 20 wird vernachlässigt) Der Faktor ist mit 190 gefunden und kann zur Berechnung der Primärzahl und Flexzahlen eingesetzt werden.
Die einzelnen Schritte nochmals in Worte gefasst:
Zur Erleichterung der Berechnungen werden alle Zahlen auf eine durch 10 teilbare Zahl auf- oder abgerundet.
Bei der Vorgabe wird die letzte Ziffer durch eine 0 ersetzt.
Von der Vorgabe wird 3*9=27 rd. 30 abgezogen. 3*9 (auch 3*7) gehört zur größten Flexzahl in Zelle 8.
Die so reduzierte Vorgabe wird durch 3 geteilt und der Faktor ist gefunden. Ein eventuell entstehender Rest wird nicht weiter beachtet. Die 3 ist die Multizahl für Zelle 8.
Zurück zur Berechnung der Primärzahl und der Flexzahlen.
Die Primärzahl ist 6*9+6*190=54+1140=1194
Addiert man die Vorgabe dazu, erhält man 1194+621=1815, die magische Summe, die über das Quadrat geschrieben wird.
Nun werden die Flexzahlen berechnet.
Die Flexzahl für Zelle 14 wird 1*9=9+1*190=199,
für Zelle 11 2*9+2*190=18+380=398 und
für Zelle 8 3*9+3*190=27+570=597.
Die übrigen leeren Zellen werden durch Addition oder Subtraktion von n*9 wie bisher berechnet.
Eine einfachere Berechnung ist möglich, in dem die Hunderter der Vorgabe mit 30 multipliziert werden. Im Beispiel wäre das dann 6*30=180, was lediglich um 10 kleiner ist als der genaue berechnete Faktor von 190.
Die erste Zeile eines so berechneten Quadrates wäre bei einer Schlüsselzahl 9:
und bei einer Schlüsselzahl 7
was durchaus akzeptiert werden kann.
Die Primärzahlen würden 6*180+6*9 = 1134, bzw. 6*180+6*7 = 1122 sein.
Diese vereinfachte Rechenweise ist nur gültig für Vorgaben größer 200. Bei einer Vorgabe 200 wird die Flexzahl für Zelle 8 = 3*60+3*9 = 207. Allerdings darf die Vorgabe selbst nicht 207 sein, was sehr unwahrscheinlich sein dürfte.
Die Berechnungen bei einer 3-stelligen Vorgabe sind durchaus noch machbar.
Von noch größeren Vorgaben sollte jedoch abgesehen werden. Die Gründe sind nicht nur mathematische, sondern auch die Tatsache, dass mit zunehmender Größe der Zahlen das Interesse des Publikums abnimmt, da es weniger die Vorgänge nachvollziehen kann.
Vorgabe der magischen Summe
Die Berechnung eines magischen Quadrates bei Vorgabe einer magischen Summe ist die schwerste Variante dieser Methode. Das Problem ist die Findung der richtigen Primärzahl, denn die Zahl für Zelle 1 wird im Umkehrverfahren berechnet, wobei von der magischen Summe die Primärzahl abgezogen wird.
Da die Primärzahl in der Grundvariante bereits 114 ist, sollte die Vorgabe eine 3-stellige Zahl größer 200 sein.
Die weiteren Erläuterungen erfolgen mit einer Vorgabe von 457.
Würde man die Berechnungen mit den Parametern der Grundvariante vornehmen, so wäre die Zahl in der 1. Zelle 457-114=343 und die Flexzahlen 19; 38 und 57.
Ein mit diesen Werten erstelltes Quadrat würde 4 Zahlen >300 und 12 Zahlen <100 enthalten, was kaum akzeptiert werden kann.
Es müssen die Zahlen für Zelle 1 und Zelle 8 angeglichen werden, wobei die Zahl in Zelle 1 die größere bleiben muss.
Eine kleinere Zahl als 457 für Zelle 1 erfordert eine Erhöhung der Primärzahl durch einen größeren Faktor. Die Erhöhung kann nicht so einfach vorgenommen werden, denn jede Erhöhung des Faktors hat auch eine Vergrößerung der Flexzahl in Zelle 8 zur Folge. Eine einfache mathematische Lösung musste gefunden werden.
Als Formel dafür kann Fa = (V-9*S) /9 eingesetzt werden.
Es bedeutet: Fa = Faktor; V = Vorgabe; S = Schlüsselzahl
Die 9 ergibt sich aus 6+3, 6 ist die Summe der 3 Multizahlen, die in die Primärzahl eingeht und 3 ist die Multizahl für die Flexzahl in Zelle 8.
Der Grundgedanke der mathematischen Lösung geht davon aus, dass die Primärzahl sich aus 6*S und 6*Fa zusammensetzt. In der Flexzahl 8 ist der Faktor 3-mal enthalten, in beiden Zahlen zusammen 9-mal.
Wird von der Vorgabe der Wert 9*S abgezogen, bei einer gewählten Schlüsselzahl 9 ist das 9*9=81 ~ 80, so erhält man den Rest, der als Gesamtfaktor im Verhältnis 6 zu 3 auf die Primärzahl und die Flexzahl 8 zu verteilen ist. Diese Betrachtungsweise ist in die Formel eingeflossen.
Daraus ergeben sich für das Beispiel folgende Zahlen:
- 457 rd. 450 = Vorgabe
- 9 = gewählte Schlüsselzahl
- 81 rd. 80 = 9*9 (Schlüsselzahl*Summe der Multizahlen aus Primär- und Flexzahl 8.)
- 450-80 = 370 = Anteil in der Vorgabe, der ein Mehrfaches des Faktors ist.
- 370/9 = 40, Rest 10. Damit ist der Gesamtfaktor mit 40 gefunden.
Der Rest wird nicht weiter berücksichtigt.
9 ist hier die Summe der Multizahlen und nicht die
Schlüsselzahl!
6*9+6*40 = 54+240 = 294 die Primärzahl.
457-294 = 163 die Zahl für Zelle 1. (Hier dürfen die Zahlen nicht gerundet werden!)
1*9+1*40 = 9+40 = 49 die Flexzahl für Zelle 14.
2*9+2*40 = 18+80 = 98 die Flexzahl für Zelle 11
3*9+3*40 = 27+120 = 147 die Flexzahl für Zelle 8
Damit sind alle Zahlen für die 1. Zeile berechnet und eingetragen.
Die Zahlen für die weiteren Zellen werden wie bekannt ermittelt und eingeschrieben.
Das fertige Quadrat mit der vorgegebenen magischen Summe von 457 ist das rechte. (Siehe nächste Seite)
Das linke Quadrat zeigt die Situation nach dem Anschreiben der magischen Summe und der berechneten Zahl für Zelle 1.
Das Topquadrat ist als Orientierung gedacht und muss einwandfrei erlernt sein.
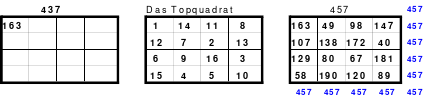
In den unten abgebildeten Tabellen sind die Berechnungen bei Wahl der Schlüsselzahlen 9 und 7, sowie einem Faktor 40 aufgeführt.
Die Zahl für die Zelle 1 würde bei Einsatz der Schlüsselzahl 7 und gleicher Vorgabe 457-282 = 175 werden.
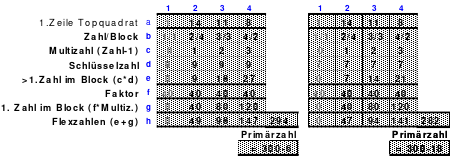
Eine Nachbetrachtung
Die Berechnungen bei der Vorgabe einer magischen Summe sind wegen der Anpassung nicht so einfach wie die bei Vorgabe einer Zahl für die Zelle 1. Das kann für Anfänger vielleicht dazu führen, dass von solchen Berechnungen Abstand genommen wird.
Mag rät in diesem Fall mit kleineren Vorgaben zu arbeiten, in dem um eine 3-stellige Zahl kleiner 200 gebeten wird. Man kann ja darauf hinweisen, dass immerhin noch zwischen 100 Zahlen gewählt werden kann.
Die Berechnungen sollten dann mit der Schlüsselzahl 7 und einem Faktor 10 erfolgen. Bei Vorgaben kleiner 150 kann es dabei zu doppelten Zahlen kommen, Entweder man nimmt die Möglichkeit in Kauf, oder setzt als Faktor 5 ein.
Die folgenden 3 Quadrate wurden nach diesen Gesichtspunkten erstellt.
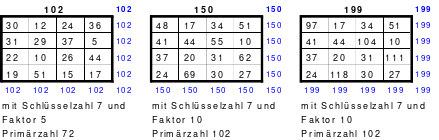
Die Zahlen für die Zelle 1 sind beim linken und mittleren Quadrat zwar kleiner als die Flexzahl in Zelle 8, ist aber nach Abzug der Schlüsselzahl 7 von der Flexzahl größer, was zulässig ist.
Für Wiederholungen ist dann die Schlüsselzahl 9 einzusetzen. Allerdings verschiebt sich dann die Grenze zur günstigen Vorgabe von 150 auf rd. 160 (genau 163). Bei Vorgaben kleiner 120 (genau 117) müsste sogar auf 1 als Faktor ausgewichen werden. Die Schlussfolgerung ist, man nimmt doppelte Zahlen, die sehr selten auftreten können, in Kauf, oder man bittet um eine Vorgabe zwischen 200 und 300.
Mehrfach wurde ein Wechsel des Faktors genannt. Dazu muss erklärt werden, dass Zahlen, die ein Mehrfaches der Schlüsselzahl sind, nicht infrage kommen. Das trifft auch auf solche zu, die mit der Schlüsselzahl einen gemeinsamen Nenner haben können. Das sind bei der Schlüsselzahl 9 die Zahlen 3 und 6 die nicht als Faktor eingesetzt werden können.
Eine nennenswerte Erkenntnis.
Man muss kein Mathematiker sein um zu erkennen, dass die Berechnung der Flexzahlen und auch der Primärzahl, einer Multiplikation mit mehrstelligen Schlüsselzahlen mit einer Endziffer 9 oder 7 entspricht.
Denn die Berechnung M*S+M*Fa = Fl ist auch M*(S+Fa) = Fl.
Die Berechnungen der übrigen Zahlen erfolgten dagegen nur mit einstelligen Schlüsselzahlen.
Das bedeutet, dass die Flexzahlen durch freie Wahl, unter Beachtung der Vorgaben, gewählt werden und auch beliebige Schlüsselzahlen zum Einsatz kommen könnten. Die Schlüsselzahlen dürfen jedoch nicht so groß sein, dass nach erforderlichen Abzügen negative Zahlen entstehen.
So könnte bei Vorgabe der magischen Summe diese einfach in 4 ungleiche Zahlen zerlegt und in die 1. Zeile eingesetzt werden. Anschließend wird eine geeignete Schlüsselzahl gewählt und für die Berechnung der übrigen Zahlen verwendet.
Analog könnte mit einer Vorgabe für die 1. Zelle verfahren werden, indem in die Zellen 14, 11 und 8 unterschiedliche, jedoch kleinere Zahlen als die Vorgabe eingesetzt werden. Die magische Summe wird dann durch Addition der Zahlen in der 1. Zeile errechnet.
Eine solche Lösung ist schwieriger und damit weniger geeignet, was insbesondere bei Verwendung eines Quadrates der 5., oder gar der 7. Ordnung zutrifft.
Der Einsatz mehrstelliger Schlüsselzahlen ist dagegen durchaus möglich. Sie erfordern zwar eine höhere Leistung, führen aber dafür zu breiter gefächerten Zahlen. Das zeigen die beiden Quadrate.
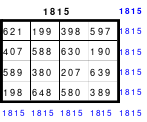
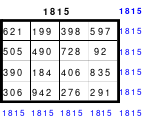
Links, das im Abschnitt “Eine 3-stellige Vorgabe” mit der Schlüsselzahl 9 gebildete Quadrat. Das rechte entstand mit der Schlüsselzahl 107. In beiden Quadraten sind die Flexzahlen gleich.
Im linken Quadrat sind Zahlen von 190 bis 648 enthalten, im rechten sind es die Zahlen 92 bis 942.
Ob das Ergebnis des Einsatzes einer 2-stelligen Schlüsselzahl, was mit erhöhtem Rechenaufwand verbunden ist, vorteilhafter ist, muss jeder selbst entscheiden.
Mag entscheidet sich nicht dafür, weil die einstelligen Schlüsselzahlen bereits ein ausgeglichenes Bild ergeben.
Eine Schlussbetrachtung
Sicher kann man darüber streiten, ob die im “Kleinen 1x1” beschriebenen Lösungen, die auch den Einsatz großer Vorgaben ermöglichen, genauso gut, oder sogar besser sind, als die Methode “Einfach Clever”. Das kann aber nur für das Topquadrat gelten, das entsprechend seiner Größe auswendig erlernt werden kann. Die Zahlenfolge eines 5er Quadrates auswendig zu beherrschen dürfte schwieriger sein und beim 7er nahezu unmöglich. Das bedeutet, dass die bevorzugte zeilenweise Eintragung der Zahlen entsprechend der “Hohen Schule”, bei diesen Quadraten nicht möglich ist. Mit der Methode “Einfach Clever” ist das jedoch zu machen, ohne die Zahlenfolge im Quadrat auswendig gelernt zu haben.
6.3.7. Das Tauschquadrat * *
Zur Vorführung
Mag zeigt 16 Tafeln mit Zahlen auf Vorder- und Rückseite mit dem Hinweis, dass keine der Zahlen doppelt vorkommt. Er bringt die Tafeln durcheinander und bittet einen Zuschauer die Tafeln ganz beliebig in ein Gestell einzusetzen und zwar so, dass ein Quadrat mit 4 mal 4 Zahlen entsteht.
Während der Zuschauer der Bitte nachkommt, zeigt er weitere 15 Tafeln, die auf einer Seite unterschiedliche, größere Zahlen enthalten. Von einem weiteren Zuschauer lässt er eine Tafel auswählen, die er in das Gestell über das Quadrat einsetzen soll.
Das so entstandene Quadrat ist nicht magisch. Die Reihensummen entsprechen auch nicht der Zahl, die der 2. Zuschauer ausgewählt hat. Dieses Quadrat ist das Startquadrat.
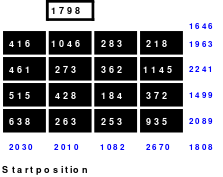
Nun beginnt Mag die Tafeln zügig auszutauschen und zum Teil auch zu wenden.
Dazu benötigt er höchstens 4 Minuten und er hat ein magisches Quadrat gebildet, dessen magische Summe der Vorgabe von 1798 entspricht.
Auch die Summen aller 4 Zahlen der 2 x 2 großen Quadrate in den Ecken und in der Mitte entsprechen der magischen Summe von 1798.
Das so entstandene Quadrat ist unten abgebildet.
(Mag hat Tafeln in schwarz mit weißer Schrift gewählt. Die Tafeln mit den magischen Summen in weiß mit schwarzer Schrift, was natürlich nicht bindend ist.)
Die Lösung
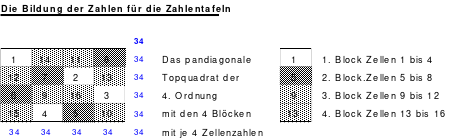
Analyse und Ergebnis
Mag hat alle möglichen Varianten des Einsatzes der Blöcke mit Vorder- und Rückseite durchgearbeitet und die dabei entstandenen magischen Summen erfasst. Doppelte Ergebnisse hat er gestrichen. Alle Ergebnisse sind in der folgenden Tabelle dargestellt.
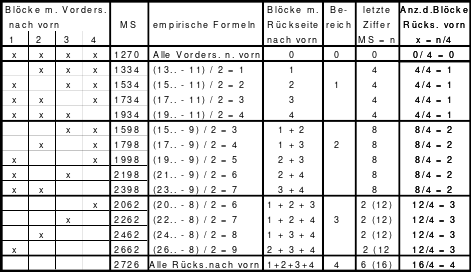
Werden alle Blöcke mit der Vorderseite eingesetzt, ergibt sich 1270 als magische Summe. Wird als Block 1 die Rückseite eingesetzt, so wird die MS 1334. Werden z. B. in die Blöcke 2 und 3 die Rückseiten eingesetzt, wird die MS 1798 groß.
Mittels empirischer Formeln wird eine Kennzahl berechnet, die der Summe der Blockzahlen entspricht, die mit der Rückseite einzusetzen sind. Diese Formel ist
(x - y) / 2 = n.
x ist dabei die Zahl aus den beiden ersten Ziffern der MS und y eine Variable, die sich aus der letzten Ziffer der MS ergibt. Dabei sind 3 Bereiche wichtig. Bei einer letzten Ziffer der MS von 4 ist y = 11; bei 8 = 9 und bei 2 = 8. (Diese Werte muss man sich gut merken.)
Allerdings sind die Kennzahlen nicht immer eindeutig. So kann die Kennzahl 7 bedeuten, dass die Blöcke 3 und 4, aber auch 1, 2 und 4 mit der Rückseite nach vorn eingesetzt werden müssen. Welche Lösung gilt, kann berechnet werden, indem die letzte Ziffer der MS durch 4 geteilt wird. Dabei sind die nicht ganzzahlig durch 4 teilbaren Endziffern 2 und 6 um 10 zu erhöhen. Werten Sie bitte obige Tabelle aus um sich mit der Materie vertraut zu machen.
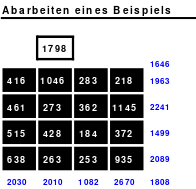
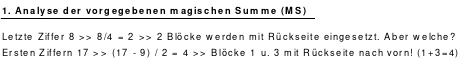
Zum Schluss
Mag ist der Meinung, dass dieses Rechenexperiment nur schwierig erscheint, aber bei eingehender Auswertung durchaus als machbar erkannt wird. Das Experiment ist außergewöhnlich und deshalb mit Sicherheit ein Höhepunkt in Ihrem Programm der Rechenkunst. Und sollte es für Sie doch zu schwer sein, dann verzichten Sie auf den Bereich 3. Damit gibt es für die Anzahl der Rückseiten nur noch eine Lösung. Jedoch reduziert sich dann die mögliche Anzahl der magischen Summen auf 10. Eine weitere Reduzierung sollte nicht vorgenommen werden.
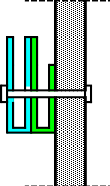
Es ist günstig, dem Zuschauer das Einsetzen der Tafeln zu zeigen.
6.3.8. Primzahlenquadrate der 4. Ordnung * *
Die 3-fache Vorgabe * *
Nachdem die Jury gebildet wurde, übergibt Mag dem mitwirkenden Zuschauer ein Karteikästchen mit 48 Karten und führt dazu aus: “In diesem Kästchen befinden sich 48 Karten mit je 3 Zahlen. 2 davon sind Primzahlen.” Er entnimmt 2 oder 3 Karten und zeigt diese vor, mit dem Hinweis, dass auf den Karten unterschiedliche Zahlen zu finden sind. Er führt weiter aus: “Es können evtl. Zahlen doppelt vorkommen, aber niemals eine gleiche Kombination der 3 Zahlen. Ich werde versuchen, aus 3 vorgegebenen Zahlen ein magisches Primzahlen-Quadrat zu konstruieren. Damit ich diese schwierige Aufgabe lösen kann, bitte ich um äußerste Ruhe.”
An den Mitwirkenden wendet er sich mit den Worten: “Bitte entnehmen Sie eine beliebige Karte und schreiben Sie die größere Zahl über das Quadrat.”
Der Zuschauer entnimmt die Karte mit den Zahlen 25432, 10627 und 619. Über das Quadrat schreibt er die Zahl 25432.
Jetzt bittet Mag den Zuschauer: “Wählen Sie eine von den kleineren Zahlen und schreiben Sie diese in eine beliebige Zelle des Quadrates.”
Der Zuschauer schreibt in die 3. Zelle der 2. Zeile die Zahl 10627.
Danach bittet er den Zuschauer ihm die 3. Zahl zu nennen. Der Zuschauer nennt die Zahl 619 die Mag in eine weitere Zelle einsetzt. Anschließend füllt er alle leeren Zellen mit Zahlen aus, bis das Quadrat fertig ist. Alle Zahlen sind Primzahlen und kommen nur einmal vor. Die Jury kann bestätigen, dass die geprüften Reihen alle die Summe 25432 haben. Auch die geprüften geteilten Diagonalen und damit ist das Quadrat ein pandiagonales magisches.
Wird das berechnete Quadrat durch senkrechte und waagerechte Teilung geviertelt, so ergeben die 4 Zahlen jedes Viertels ebenfalls die magische Summe.
Sichtlich entspannt nimmt Mag den Beifall entgegen.
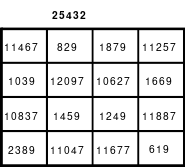
Sicherlich haben Sie erkannt, dass dieses Rechenkunststück einen sehr hohen Schwierigkeitsgrad hat. Wenn dem so ist, hat Mag mit seinem Theater erreicht was er wollte, denn dieses Rechenexperiment ist wesentlich leichter als es scheint.
Mag setzt hier die Primzahlenreihen mit 8 bis 10 Gliedern und der Differenz von 210 ein. Das sind leider nur 7 Reihen die Mag aus den Primzahlen bis 50000 herausgefiltert hat. Deshalb nutzt Mag alle möglichen Reihen mit 8 Primzahlen, das heißt, die 10er Reihe enthält 3 Reihen die mit 199, 409 und 619 beginnen. Die infrage kommenden ersten Zahlen der 8er Reihen sind in der nachfolgenden Tabelle fett hervorgehoben. So sind insgesamt 11 Reihen mit je 8 Zahlen möglich.
Die arithmetischen Primzahlenreihen mit 8 bis 10 Gliedern und einer Differenz zwischen den Gliedern von 210
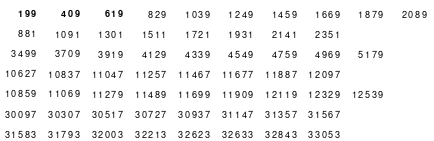
Um die 48 Kombinationen zu erhalten hat Mag alle ersten Zahlen mit allen ersten Zahlen der anderen Reihen kombiniert und die dazugehörige magische Summe berechnet. Diese errechnet sich wie folgt:
2a + 2b + 210 x 14 = mS
im Beispiel ist das 2 x 10627 + 2 x 619 + 210 x 14 = 25432
Die magischen Summen mit den dazu gehörenden 2 ersten Primzahlen hat Mag auf die 48 Karten geschrieben.
Und hier ist die Tabelle für die 48 Karten, die der Zuschauer bekommt. Sie enthält die magischen Summen als die jeweils größten Zahlen und die zwei ersten Prim-Zahlen der möglichen 8er Reihen.
Die 48 Karten mit den Zahlenkombinationen
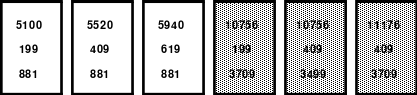
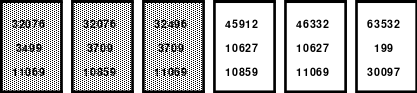
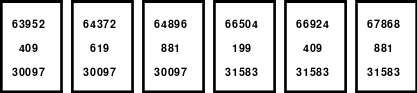
Dazu noch einige Erläuterungen.
Zum Einsatz kommt das Topquadrat, ein pandiagonales Quadrat der 4. Ordnung.
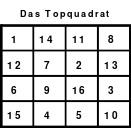
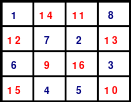
Die Zahlenfolge im Topquadrat muss bestens beherrscht werden.
Das Topquadrat setzt sich aus 4 Blöcken, 1 bis 4, 5 bis 8, 9 bis 12 und 13 bis 16 zusammen.
Mag fasst den 1. und 2. Block im Topquadrat zu einem Block, den 1. zusammen. (Siehe blaue Zahlen). Ebenso den 3. und 4. zum 2. Block. (Siehe rote Zahlen). In das Topquadrat werden nämlich nicht 4 Reihen mit je 4 Zahlen eingesetzt, sondern 2 Reihen mit je 8 Zahlen.
Das Topquadrat ist plandiagonal. Es können Spalten und/oder Zeilen versetzt werden, wobei das Quadrat stets plandiagonal bleibt.
Das bedeutet, dass jede vom Zuschauer gewählte Zelle als Zelle 1 im Topquadrat gewertet werden kann. Die 2. Zahl setzt Mag in die Zelle 9 ein, denn diese ist die 1. Zelle im nun 2. Block. Die Zelle 9 befindet sich 1 Feld nach rechts und 2 Felder nach unten. Mag muss ausgehend von der Zelle 9 nun eine Zelle nach der anderen mit Primzahlen ausfüllen.
Bezogen auf das Beispiel ist rechts von Zelle 9 die Zelle 16 und darunter die Zelle 5, d. h., die Zelle links oben ist die Zelle 5. 5 ist die 5. Zahl im 1. Block. Die Zahl 10627 in der 1. Zelle muss nun um 4 x 210 = 840 erhöht werden. Das Ergebnis 11467 wird eingeschrieben.
Die Zelle neben der 5. ist die 10. Das ist die 2. Zahl im 2. Block. Mag muss deshalb die Zahl 619 in Zelle 9 um 1 x 210 erhöhen und erhält so 829. So wird fortgefahren bis alle Zellen eine Zahl enthalten und das Quadrat ist fertig. Mag war es gelungen, 3 Vorgaben so in ein Quadrat einzuordnen, dass ein pandiagonales magisches Primzahlenquadrat entstand, dessen magische Summe der Vorgabe entsprach.
Die Vorteile dieser Variante gegenüber der Quadratbildung aus natürlichen Zahlen sind:
- Die vom Zuschauer eingesetzte Zahl ist immer in der Zelle 1. Es muss nicht geprüft werden ob die Zahl dem 1. oder 2. Block zugeordnet werden muss.
- Der Vorführende muss sich nicht die ersten Zahlen von 3 weiteren Blöcken merken. Die ersten Zahlen, der jetzt nur noch 2 Blöcke, nennt ihm ja der Zuschauer.
- Auch die Berechnung der magischen Summe entfällt. Diese schreibt ja der Zuschauer selbst über das Quadrat.
Die Nachteile sind:
Die in den Kombinationen mehrfach zu findenden Primzahlen können dem aufmerksamen Zuschauer auffallen, obwohl die Karten gut gemischt wurden. Deshalb hat Mag anfangs darauf hingewiesen, das Zahlen mehrfach vorkommen können, aber niemals eine gleiche Kombination.
Den beiden Zahlen müssen bis zum 7-fachen von 210 zugeschlagen werden. Das dürfte aber nicht schwierig sein, zumal man die Ausgangszahl immer vor Augen hat.
Eine Erweiterung der 8er Primzahlenreihen ist nicht wahrscheinlich. Mag hat jedenfalls aus den Primzahlen von 50001 bis 100000 keine weiteren herausgefunden.
- Durch die Addition von 210 bleibt die letzte Ziffer stets gleich. Dadurch kommen jeweils 2 Endziffern 8-mal vor. In mehreren Fällen sind sogar alle 16 Endziffern gleich.
- In 6 Fällen treten gleiche magische Summen auf. Beabsichtigt man eine Wiederholung, so sollten die entsprechenden Karten vorher herausgenommen werden.
Trotzdem ist die von Mag entwickelte Lösung brauchbar, auch wenn sie wahrscheinlich nicht für den Profi geeignet ist.
Eine Nachbetrachtung
Die zuletzt genannten Nachteile müssen nicht sein. Zur Vermeidung einer Wiederholung der magischen Summe sollten die entsprechenden Karten aus dem Kartenpack entfernt werden. Das sind die 6 blau schattierten. Es verbleiben dann immer noch 34 Karten.
Zur Vermeidung gleicher Endziffern in allen 16 Zellen könnten auch die grün schattierten 10 Karten herausgenommen werden. Die dann verbleibenden 24 Karten erachtet Mag noch als ausreichend. Mag überlässt dazu Ihnen die Entscheidung.
Vorgabe einer Primzahl * *
Mag war bestrebt, wie bei den natürlichen Zahlen, eine Lösung zu finden, die die Bildung eines 4er Primzahlenquadrates bei Vorgabe einer Primzahl ermöglicht. Er hat eine solche entwickelt. Allerdings ist sie etwas komplizierter, aber machbar.
Zum Ablauf einer solchen Vorführung:
Mag bittet um die Mitwirkung eines Zuschauers. Diesen übergibt er eine Liste mit dem Hinweis:
“Auf dieser Liste sind Primzahlen kleiner 1000. Bitte wählen Sie eine beliebige aus und nennen Sie mir diese.”
Der Helfer nennt die Primzahl 389, die Mag in die erste Zelle der 1. Zeile einsetzt. Danach schreibt er über das Quadrat die Zahl 1738. Anschließend trägt er fortlaufend Zahlen in die Zellen des Quadrates ein, bis alle Zellen eine enthalten.
Das fertige Primzahlenquadrat der 4. Ordnung ist das nachfolgende.
Mag erklärt: “Dieses Quadrat ist magisch. Die magische Summe beträgt 1738, wie ich sie anfangs über das Quadrat geschrieben habe.”
Er bittet die Jury das zu überprüfen, die dann diese Aussage bestätigen kann.
Die Lösung
Mag hat alle Primzahlenreihen mit 4 und mehr Gliedern und einer Differenz von 30 aus den Primzahlen kleiner 1000 ermittelt.
Diese sind: 5 Reihen mit der Endziffer 1
2 Reihen mit der Endziffer 3
6 Reihen mit der Endziffer 7 und
2 Reihen mit der Endziffer 9
Dabei sind Primzahlenreihen mit bis zu 6 Gliedern zu finden. Diese ermöglichen die Gestaltung von mehreren Reihen mit je 4 Gliedern. Das ist möglich, da der Zuschauer ja nur eine Zahl nennt. Damit kann es auch nicht zu doppelten Primzahlen im Quadrat kommen.
Alle ersten Primzahlen der möglichen 4er Reihen sind hervorgehoben und wurden nach Größe sortiert in die Liste übernommen. In der Liste befinden sich 26 Primzahlen. Dabei fehlen die Zahlen der Reihen mit 4 Gliedern und den ersten Zahlen 23, 349 und 797. Diese beansprucht Mag für sich.
Die Primzahlenreihen und die Liste:
Die Lösung ergibt sich aus einer Analyse des Topquadrates, links. Rechts sind die einzelnen Schritte der Analyse aufgezeigt.
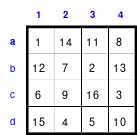
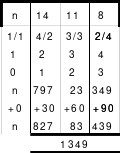
Die 1. Zeile entspricht der 1. Zeile des Topquadrates, wobei lediglich für die 1 ein n eingesetzt ist. Das n steht für die später vom Helfer gewählte und genannte Primzahl. Die 2. Zeile gibt an, zu welchem Block die Zahl gehört und die wievielte es im Block ist. So ist die 14 eine Zahl des 4. Blockes und zwar die 2. im Block und die 8 ist die 4. Zahl im 2. Block. Da die Blöcke vernachlässigt werden können, enthält die 3. Zeile nur noch den Stellenwert im Block. In der nächsten Zeile ist angegeben um wie viel die Zahl größer ist. als die 1. im Block. So ist die 11 um 2 größer als 9, die 1. Zahl im 3. Block. In der nächsten Zeile sind nach n die ersten Zahlen der
vereinnahmten 3 Primzahlenreihen in der Folge 797, 23 und 349 enthalten. Im Topquadrat ist die Differenz zwischen den Zahlen 1. Die Differenz in den Primzahlenreihen ist dagegen 30. Deshalb müssen diese Zahlen um 30, 60 und 90 erhöht werden, wodurch die Zahlen 827, 83 und 439, in der letzten Zeile, entstehen.
Diese 3 Zahlen ergeben als Summe 1349. Diese Summe 1349 und die 1. Zahlen der Reihen, 797, 23 und 349 (einfacher 23, 349 und 797) muss sich der Vorführende gut merken. Sie werden auch in weiteren Aufführungen immer wieder eingesetzt.
Doch nun zur Anwendung der Erkenntnisse. Beachten Sie dazu das fertige Primzahlenquadrat rechts.
Nennt der Helfer die Zahl 389, so schreibt Mag diese in die Zelle links/oben. Zu dieser 389 addiert er die Summe 1349 und erhält 1738, die er als magische Summe über das Quadrat schreibt. In die 2. Zelle setzt Mag eine der ersten Zahlen, hier die 797 + 30 = 827 ein. Weiter mit 23 + 60 = 83 und in die 4. Zelle 349 + 90 = 439. Damit ist die 1. Zeile fertig und sie hat als magische Summe den Wert 1738.
Die leeren Zellen könnten nun ganz einfach durch Komplettierung der einzelnen Blöcke erfolgen. Das wäre ausgehend von der Zelle 1 mit der 389 + 30 = 419 für Zelle 2, + 30 = 449 in Zelle 3 und + 30 = 479 in Zelle 4 des 1. Blockes. Die nächste Zahl in der 1. Zeile ist die 827 und die Zelle 14. Zuerst wird zurückgegangen, d. h. zur Zelle 13 und dort wird 827 - 30 = 797 eingesetzt. Dann vorwärts von Zelle 14 zur Zelle 15 und 16 in die die Zahlen 827 + 30 = 857 und 857 + 30 = 887 kommen. Weiter zur 3. Zahl, die 83 in Zelle 11. Rückwärts zur Zelle 10 mit der Zahl 83 - 30 = 53 und zur Zelle 9 mit der Zahl 53 - 30 = 23. Dann vorwärts von 11 zur 12 in die 83 + 30 = 113 einzusetzen ist. Von der letzten Zahl 439 in der oberen Reihe, die 8 und damit die letzte Zahl des 2. Blockes, rückwärts zu den Zellen 7, 6 und 5 mit den Zahlen 409, 379 und 349, womit das Quadrat fertig ist.
Mag bevorzugt diese Art der Fertigstellung nicht. Sie ist zwar leicht, aber der aufmerksame Zuschauer kann erkennen, dass die Zahlen immer um den Wert +/-30 verändert werden, wodurch das Experiment schnell als leichte Sache abgetan werden kann.
Mag ist für eine Eintragung entsprechend der “Hohen Schule”, also Zeile um Zeile.
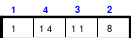
Dazu muss die Zuordnung der Zellen zu den jeweiligen Blöcken bestens beherrscht werden. Auch muss man wissen, an welcher Stelle die dazugehörige Zahl in der oberen Zeile zu finden ist. Die obere Skizze gibt dazu Auskunft (blaue Zahlen). Die folgenden Berechnungen werden in verständlicher Kurzform beschrieben. Die in Klammer () gesetzten Berechnungen veranschaulichen die Ermittlung der Differenzen zwischen den jeweiligen Zellenzahlen.
Begonnen wird mit Zeile 2, 1. Zelle, die Zelle 12 im Topquadrat:
Zelle 12 = 3. Block, von Zahl aus Zelle 11 = 83 >> 83 + 30 = 113 (12-11=1)
Zelle 7 = 2. Block. von Zahl aus Zelle 8 = 439 >> 439 - 30 = 409 (8-7=1)
Zelle 2 = 1. Block, von Zahl aus Zelle 1 = 389 >> 389 + 30 = 419 (2-1=1)
Zelle 13 = 4. Block, von Zahl aus Zelle 14 = 827 >> 827-30 = 797 (14-13=1)
Zur Zeile 3:
Zelle 6 = 2. Block, von Zahl aus Zelle 8 = 439 >> 439 - 2*30 = 379 (8-6=2)
Zelle 9 = 3. Block. von Zahl aus Zelle 11 = 83 >> 83 - 3 * 30 = 23 (11-9=3)
Zelle 16 = 4. Block, Zahl aus Zelle 14 = 827 >> 827 + 2*30 = 887 (16-14=2)
Zelle 3 = 1. Block, von Zahl aus Zelle 1 = 389 >> 389+ 2*30 = 449 (11-9=3)
Zur Zeile 4
Zelle 15 = 4. Block, von Zahl aus Zelle 14 = 827 >> 827+ 30 = 857 (15-14=1)
Zelle 4 = 1. Block, Zahl aus Zelle 1 = 389 >> 389 + 3*30 = 479 (4-1=3)
Zelle 5 = 2. Block, Zahl aus Zelle 8 = 439 >> 439 - 3 * 30 = 349 (8-5=3)
Zelle 10 = 3. Block, von Zahl aus Zelle 11 = 83 >> 83 - 30 = 53 (11-10=1)
Diese Form der Berechnung mag etwas schwieriger sein, sie ist aber eleganter und weniger durchschaubar.
Eine Nachbetrachtung
Mag ist überzeugt, dass die von ihm ausgearbeitete Variante zur Bildung eines magischen Quadrates mit Primzahlen, bei Vorgabe nur einer Primzahl, eine gelungene ist.
Allerdings muss auch auf die Nachteile aufmerksam gemacht werden.
So sind die möglichen Vorgaben auf lediglich 26 Primzahlen begrenzt, obwohl es insgesamt 168 Primzahlen kleiner 1000 gibt. Das wirft Fragen auf und kann dazu führen, dass Ihnen eine Primzahl außerhalb der Tabelle vorgegeben wird, was Ihrerseits nicht erkannt werden kann, denn Sie können sich kaum alle 26 Primzahlen merken. Wenn Sie im guten Glauben das Quadrat erstellt haben, ist es zwar magisch, aber es sind in der Regel 3 Zahlen keine Primzahlen.
Es ist jedoch höchst unwahrscheinlich, dass eine Zahl außerhalb der Liste genannt wird.
Ein weiterer Nachteil ist, dass das entstandene Quadrat zwar magisch, aber nicht mehr pandiagonal ist. Der Grund dafür ist, dass das Topquadrat nur teilhomogen ist und die Differenzen von Block zu Block nicht einheitlich groß sind. Deshalb ist es nicht möglich, dass der Gast eine Zelle für den Anfang bestimmen kann.
Dieses Experiment sollte nicht wiederholt werden!
Das linke Quadrat ist eine Wiederholung mit der Vorgabe 557. Mag hat die Eintragungen in die folgenden Zellen verändert. In Zelle 14 hat er dir Primzahl 349 + 30 = 379, in die Zelle 11, 797 + 60 = 857 und in die Zelle 8, 23 + 90 = 113 eingesetzt. Das daraus entstandene Quadrat ist auf den ersten Blick ungleich dem rechten Quadrat, aber bei genauer Betrachtung sind nur die magische Summe, die Vorgabe und die aus der Vorgabe berechneten Zahlen für die Zellen 2, 3 und 4 andere.
Alle übrigen 12 Zahlen sind in beiden Quadraten gleich. Sie sind nur ungleich eingeordnet. Das ist auch logisch, denn es werden in die Blöcke 2 bis 4 die gleichen Primzahlenreihen eingesetzt.
Zum Abschluss
möchte Mag noch bemerken, dass die für die Zellen 14, 11 und 8 von Mag beanspruchten Primzahlen 23, 349 und 797 nicht verbindlich sind. Im Ergebnis weiterer Untersuchungen hat Mag die Primzahlen 13, 307 und 401 als günstigere gefunden. Die Summe dieser 3 Primzahlen beträgt 721. Addiert man 180 (6 * 30) zu dieser Summe, erhält man 901 und das ist auch 900 + 1.
Mit Hilfe dieser Summe ist die Berechnung der magischen Summe viel leichter. So wird aus der Vorgabe 557 die magische Summe 1458.
Allerdings ändert sich dadurch auch die Liste der Primzahlen. Oben rechts die neue Liste mit nur noch 24 Primzahlen.
Weitere günstige Zwischensummen sind:
1111 mit den 3 Primzahlen 23, 307 und 601 oder 181, 349 und 401
1115 mit den 3 Primzahlen 41, 307 und 587 oder 167, 181 und 587
Bei einer Wahl dieser Summen und Primzahlen muss die Liste der Vorgabezahlen entsprechend geändert werden.
Eine Nachbetrachtung
Als zusätzliche Variante wäre eine 2. Liste mit den möglichen magischen Summen. Diese kann einem weiteren Zuschauer übergeben werden. Als eine Art der Wiederholung nennt dieser die magische Summe und der Vorführende berechnet durch Abzug der Zwischensumme die Primzahl für die Zelle 1. Alles andere läuft dann wie bei der Vorgabe einer Primzahl für Zelle 1 ab.
(Mag bittet Sie, nicht auf den Gedanken zu kommen, den unteren Teil der Kreide mit kunterbuntem Geschenkpapier zu umhüllen und dort heimlich die 3 Primzahlen und die Zwischensumme zu notieren. Das wäre unseriös. Als Rechenkünstler müssen Sie sich die 4 Zahlen merken können.)
Die Doppelvariante * *
Wem die Variante mit der Vorgabe einer Primzahl zu schwer ist, dem bietet Mag eine leichtere Variante mit der Vorgabe von 2 Zahlen an. Diese 2 Zahlen sind eine Primzahl und die magische Summe, die keine Primzahl sein kann.
Man muss sich ja nicht nur die 3 Primzahlen merken, sondern auch die Zwischensumme die sich aus diesen 3 Primzahlen plus 180 ergibt und weiter muss daraus die magische Summe berechnet werden. Das alles kann eventuell schwierig zu bewältigen sein.
Bei der 2. Variante sucht man sich 3 leicht zu merkende Primzahlen aus der Gesamtliste aus. Das könnte als Beispiel sein: 23, 107 und 401.
Die Summe der ausgewählten 3 Primzahlen plus 180 ist dann die Zwischensumme. Das wäre im Beispiel 23 + 107 + 401 + 180 = 711.
Es kommen wieder Karten zum Einsatz. In diese wird als obere Zahl die magische Summe eingesetzt. Diese ergibt sich aus der Zwischensumme plus einer der verbliebenen Primzahlen aus der Liste, die gleichzeitig als die 2. Zahl daruntergeschrieben wird. So entstehen 27 mögliche Karten.
Der Vorführende zeigt einige Karten mit dem Hinweis, dass die Zahlen auf den Karten alle unterschiedlich sind und keine 2mal vorkommt. Davon lässt er eine auswählen und lässt sich die obere Zahl nennen, die er über das Quadrat schreibt. Die 2. Zahl, eine Primzahl, wird in die Zelle 1 des Topquadrates geschrieben.
Alles andere läuft wie bekannt ab. Mag wünscht Ihnen bei der Auswertung und Anwendung viel Freude und Erfolge.
6.3.9. Primzahlen-Duos * * (Die Einmaligen)
Im Abschnitt 8. “Primzahlenquadrate...” wurden Lösungen beschrieben, die Mag nicht besonders zufrieden stellend empfand. So wurden 3 Vorgaben in Form von Karten vorgeschlagen, 2 Primzahlen für die Zellen und die magische Summe. Dabei kamen sehr große Primzahlen, bis zu 5-stellige, zum Einsatz. Auch zur Berechnung der weiteren Zahlen für die Zellen wurde das Rechnen mit dem 1- bis 3-fachen der Zahl 210 erforderlich. Das gestaltete Quadrat war oft zur Hälfte kleine und sehr große Zahlen, wobei deren Endziffern im günstigen Fall 2, oft sogar nur eine war. Bei der “Vorgabe einer Primzahl” mussten 3 Zahlen erlernt und gemerkt werden. Dabei war das Problem, dass eine Wiederholung nicht ratsam war, da es zu 75 % gleicher Zahlen, wie im vorangegangenen Experiment, kommt. Das Gleiche gilt zur “Doppelvariante“, wobei bei dieser zusätzlich zur Vorgabe eine Primzahl die Vorgabe der magischen Summe erfolgt.
Mag gelang es, eine weitere Variante zur Bildung magischer Primzahlenquadrate, zu erarbeiten, die nach seiner Auffassung die bessere Lösung ist. Allerdings kann auch hier nicht auf die Vorschläge von Primzahlen mittels Karten verzichtet werden. Vorteilhaft ist, dass die magischen Quadrate aus nur 2 vorgegebenen Primzahlen berechnet werden kann. Dabei kommen Zahlen größer als 3-stellige nicht zum Einsatz. Die Zahlen in den Zellen sind gleichmäßiger gestreut. Allerdings treten auch hier nur 1 oder 2 gleiche Endziffern auf.
Eine Wiederholung sollte nicht erfolgen, weil die Wahrscheinlichkeit der Wiederholung von Zahlen, der magischen Summe oder sogar des kompletten Quadrates groß ist. Die Ursache liegt in den wenigen Doppelprimzahlenreihen die gefunden wurden. Das wird noch in den weiteren Erläuterungen erklärt.
Aus diesen Gründen hatte Mag vor, diese Routine nicht in das Hexen 1x1 aufzunehmen. Er nimmt es wegen seiner Einmaligkeit doch auf, jedoch mit der Empfehlung diese nur einmal zu zeigen und auf eine Wiederholung zu verzichten.
Ein gedachter Ablauf
Mag zeigt ein Kartenkästchen vor, in dem sich 40 Karten mit je 2 unterschiedlichen Primzahlen befinden.
Er zeigt einige Karten davon als Beispiele und übergibt die Karten an einen bereiten Zuschauer mit der Bitte, eine dieser Karten auszuwählen und ihm zu übergeben.
Mag nennt die beiden Primzahlen 137 und 661 und schreibt diese in 2 Zellen des Quadrates und gibt die Karte an den Zuschauer zur Kontrolle zurück.
Nach einer kurzen Denkpause schreibt er über das Quadrat 15696, die magische Summe.
Danach füllt er alle Zellen mit Primzahlen aus, bis das Quadrat fertig ist.
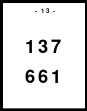
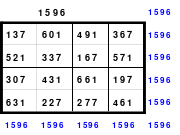
Er weist darauf hin, dass das Quadrat magisch ist, sogar pandiagonal und alle Reihen die einheitliche magische Summe von 1596 haben. Alle Zahlen im Quadrat sind Primzahlen und keine ist doppelt.
Wie hat Mag das gemacht?
Die 137 setzte er in die Zelle 1 ein und die 661 in die Zelle 16.
Beide Zahlen addiert er und multipliziert das Ergebnis mit 2 und hat so die magische Summe berechnet. 137+661=798*2=1596.
Ausgehend von Zelle 1 mit der 137, geht es zu den Zellen 2, 3 und 4, in die eine um jeweils 30 erhöhte Primzahl eingesetzt wird. (167, 197 und 227)
In die Zelle 5 wird nicht wie gewohnt 227+30=257 eingesetzt, sondern die um 50 erhöhte Zahl 227 aus Zelle 4. Das ist 227+50=277.
Jetzt können die um 30 erhöhten Zahlen 307, 337 und 367 in die Zellen 6,7 und 8 geschrieben werden.
Ausgehend von der 661 in Zelle 16 werden die um jeweils 30 reduzierten Zahlen 631, 601 und 571 in die Zellen 15, 14 und 13 eingetragen.
In die Zelle 12 schreibt Mag die Zahl 521, die er durch Subtraktion von 50 von der Zahl in Zelle 13 erhält. Im Einzelnen 571-50=521
n die Zellen 11, 10 und 9 werden die um jeweils 30 reduzierten Zahlen 491, 461 und 431eingesetzt.
Das was es schon. Die einzelnen Berechnungen der Zahlen für die Zellen wurden durch +/-30, in einem Fall mit +50 und in einem weiteren -50 vorgenommen. Die etwas schwerere Berechnung ist die Ermittlung der magischen Summe, was aber für eine “Rechenkünstler” ein leichtes sein müsste.
Warum hat Mag das so gemacht?
Folgende Ziele werden gestellt:
Es sollen keine Primzahlen größer 1000 eingesetzt werden. (Wegen der einfacheren Berechnungen und einer besseren Einbeziehung der Zuschauer)
Die Vorgaben sollen maximal 2 sein. (Je weniger Vorgaben umso höher die Leistung) Die Differenzen zwischen den Zahlen in den Reihen sollen auf 30 begrenzt werden. (Kein Rechnen mit der Differenzzahl 210) Es sollen möglichst unterschiedliche Endzahlen im Quadrat enthalten sein. (Wegen des besseren optischen Eindruckes, kann aber nicht verwirklicht werden)
Die Pandiagonalität des Topquadrates soll möglichst erhalten werden. (Um die evtl. Vorgabe der Startzelle zu ermöglichen)
Damit scheiden Primzahlenreihen mit einer Differenz von 210 und 6 aus. Bei den Reihen mit der Differenz 6 gibt es zu wenige Reihen mit 4 Zahlen.
Bleiben nur noch Reihen mit einer Differenz von 30 übrig. In denen gibt es aber keine Reihen mit 8 Zahlen. Folglich müssen statt einer Reihe mit 8 Gliedern, 2 Reihen mit 4 Gliedern zum Einsatz kommen.
Das bedeutet 4 Vorgaben, was zu viele sind. Von 2 Reihen die ersten Zahlen reservieren und merken ist auch nicht möglich, es schließt eine Wiederholung und die Erhaltung der Pandiagonalität aus.
Es war erforderlich, je 2 Primzahlenreihen zu finden, die einen gleichen Abstand zueinander haben. Diese zu finden war nicht leicht. Der Einsatz aller geraden Zahlen bis 200 als Abstandszahlen, erbrachten lediglich bei der Zahl 140 5 Reihenpaare. Diese sind in der folgenden Abbildung dargestellt.
Die ersten Zahlen dieser Paare haben einen Abstand von +140. Die letzte Zahl der linken Reihe zur ersten der rechten Reihe beträgt nur +50 und der Abstand der letzten Zahl der rechten Reihe zur ersten der linken Reihe ist -230.
Eine Erweiterung bis zur Primzahl 2000 brachte kaum Ergebnisse. So konnte mit einer Differenz von 140 nur eine weitere Doppelreihe gefunden werden. Darauf wird verzichtet und es bei 3-stelligen belassen! Die folgende Tabelle1 zeigt die Doppelreihen in Gruppe A als aufsteigende Zahlenreihe (oben) und darunter als absteigende Zahlenreihe. Werden nun alle aufsteigenden Reihen mit den anderen Reihen als absteigend kombiniert, erhält man 4*5=20 unterschiedliche Kombinationen. Allerdings treten alle Zahlen 4-mal auf. Auch kommt es mehrmals zu gleichen magischen Summen.
Um mehr als nur 20 Karten zu bekommen, wurden die oberen 4er Zahlenreihen mit den unteren getauscht. Das Ergebnis ist als Gruppe B dargestellt. Hier sind die ersten Zahlen der auf- bzw. der absteigenden Reihe andere, jedoch werden die magische Summe die gleichen wie in der Gruppe A sein. Das ist logisch, denn es handelt sich um die gleichen Zahlen in den Reihen. Damit sind insgesamt 40 Kombinationen bzw. Karten möglich. Die Karten enthalten als obere Primzahl die der aufsteigenden Reihe und als untere die der absteigenden.
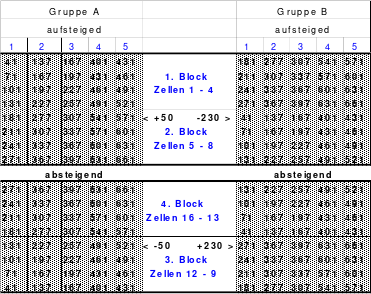
Allerdings ändern sich die Übergänge innerhalb der 2 Viererreihen von +50 zu -230 und von -50 zu +230.
Das erfordert, dass die Vorgaben erkennbar sein müssen, zu welcher Gruppe das Zahlenpaar gehört. Das hat Mag mit der nebensächlich wirkenden Kartennummerierung gelöst. Alle Karten der Gruppe A haben ungerade Kartennummern z.B. - 13 - und die der Gruppe B gerade z. B. - 8 -.
(Jetzt wissen Sie auch, warum sich der Vorführende die gewählte Karte aushändigen ließ.)
Alle 40 Kombinationen sind in der folgenden Tabelle 2 enthalten.
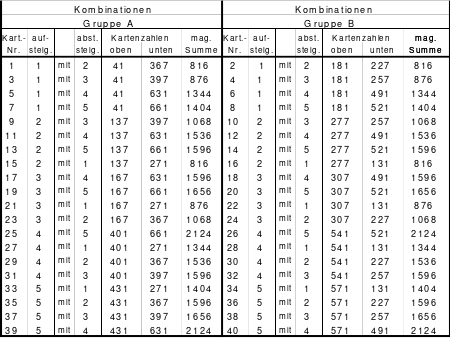
Die Tabelle enthält auch die entstehenden magischen Summen. Auch diese treten 4-fach auf. Sie ermöglichen aber auch die Erweiterung der Karten auf 80, wenn in der Gruppe A die magische Summe mit der 1. Primzahl der aufsteigenden Reihen eingesetzt werden und die der absteigenden Reihe bei der Gruppe B.
Es ist auch denkbar, beide Formen auf 40 Karten zu verteilen und dafür die Anzahl gleicher Zahlen und magischer Summen auf die Hälfte zu reduzieren.
Wenn die Karten gut gemischt werden, ist schwer zu erkennen, dass die Zahlen mehrfach vorkommen. Sicherheitshalber sollte der Vorführende darauf hinweisen, dass es zur Wiederholung einzelner Primzahlen kommen kann, aber niemals zu einer gleichen Kombination.
Auf eine Wiederholung dieses Rechenexperimentes sollte jedoch nach Möglichkeit verzichtet werden, denn die Wahrscheinlichkeit einer Wiederholung gleicher magischen Summen oder Primzahlen beträgt 10 bis 17%.
Nach all den Erläuterungen verstehen Sie die Berechnungen die Mag weiter vorn unter ”Wie hat Mag das gemacht?” beschrieben hat. Nachstehenden will Mag den Unterschied bei den Berechnungen von Beispielen aus der Gruppe A und B aufzeigen. Die Kartennummern 13 und 53 der beiden Karten verraten, dass es sich um Vorgaben aus der Gruppe A handelt. Die linke Karte enthält die Primzahlen 137 und 661. Beide addiert und mit 2 multipliziert ergibt die magische Summe von 1596. Das gleiche Quadrat entsteht bei den Vorgaben nach Karte 53. Durch Division der magischen Summe 1596 durch 2 und Abzug der Primzahl 137 wird die zweite Primzahl 661 errechnet. Beide Primzahlen, 137 und 661, bilden ein Duo der Größe 798, die Hälfte der magischen Summe von 1596.
Diese Vorgaben werden in die Zellen 1 und 16 des Topquadrates eingesetzt. Die ersten 8 Primzahlen einer Doppelreihe werden aufsteigend in die Zellen 1 bis 8 eingetragen. Dabei erhöhen sich die Zahlen um jeweils 30, außer beim Übergang zwischen den Viererreihen innerhalb der Doppelreihe, das ist von Zelle 4 mit 227 zur Zelle 5 mit 277, Hier ist die Differenz +50, Dem entspricht bei der absteigenden Reihe die Differenz zwischen den Zelle 13 und 12, allerdings nicht +50, sondern -50.
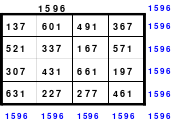
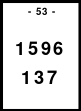
Das 2. Beispiel ist eins aus der Gruppe B.
Mag hat dieses ausgewählt, weil hier ein Problem sichtbar wird. In diesem Quadrat sind 6 Zahlen doppelt und nur 4 einzeln. Die Ursache ist in der Tabelle 1 leicht zu erkennen. In der Gruppe A sind die Primzahlenreihen als aufsteigende Reihen in den Spalten 1 bis 5 dargestellt. Dabei fällt auf, dass die ersten Zahlen der Spalten 2 und 3, sowie die Spalten 4 und 5 eine Differenz von 30 haben, um die auch die Zahlen in den einzelnen 4 Blöcken des Topquadrates erhöht werden, was zu diesen Überschneidungen führt.
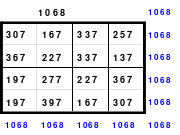
Sie haben 2 Möglichkeiten mit diesem Problem umzugehen.
1. Sie können die Karten so belassen, dürfen aber nicht behaupten, dass alle Primzahlen nur einmal vorhanden sind. Erkennt ein Zuschauer diese Situation und bemängelt diese, so können Sie erklären, dass bei den gewählten Vorgaben eine Quadratbildung in anderer Form nicht möglich ist.
2. Besser ist es und von Mag empfohlen, die Karten mit den Nummern 9, 23, 25, 39, 10, 24, 26 und 40 wegzulassen. Dann sind immerhin noch 32 Karten möglich und bei Einbeziehung der magischen Summen 64, was durchaus ausreichend ist.
An diesem Beispiel ist der veränderte Übergang zwischen den Viererreihen innerhalb der Doppelreihen ersichtlich.
So ist der Übergang von Zelle 4 mit 397 zur Zelle 5 mit 167 nicht +50, sondern -230 und von Zelle 13 zur Zelle 12 nicht +50, sondern -230.
Alle anderen Berechnungen sind die gleichen wie beim Beispiel aus der Gruppe A.
Die Primzahlenquadrate sind pandiagonal
Durch die Anwendung der Doppelprimzahlenreihen werden die Übergänge von Zelle 4 zur Zelle 5 und von Zelle 13 zur Zelle 12 im Topquadrat einheitlich zwar nicht 30, sondern 50 groß.
Damit ist die Voraussetzung für das Entstehen von pandiagonalen Quadraten gegeben. Dieser Vorteil gegenüber den anderen Primzahlenquadraten bietet die Möglichkeit, dass der Zuschauer die Zelle bestimmt, in die die erste Primzahl eingesetzt werden soll. Die 2. Primzahl wird dann 2 Zellen diagonal weiter eingetragen. Bleibt man innerhalb des Quadrates, besteht dazu nur eine Möglichkeit.
Das Non plus Ultra
Die mathematischen Grundlagen zur Berechnung der Primzahlen für die einzelnen Zellen sind gegeben und das ermöglicht die Eintragung der Zahlen entsprechend der “Hohen Schule”. Allerdings sind die Berechnungen etwas komplexer und erfordern eine höhere Rechen- und Gedächtnisleistung, weshalb diese Routine auch 2 Sterne erhalten hat. Die Bildung eines Primzahlenquadrates im Stil der hohen Schule wird anhand eines Beispiels erläutert. Dabei wird auch die Bestimmung der Eingabezelle für die 1. Primzahl eingebunden.
Wenn der Zuschauer auch noch eine Karte mit einer magischen Summe ausgewählt hat, kann die Abwicklung der Quadratbildung in einer sehr günstigen Form erfolgen. Mag nennt diese Art der Quadratbildung deshalb auch “Das Non plus Ultra”.
Auch wenn Mag diese Routine aus Altersgründen nicht vorgeführt hat, wird er die Rolle eines Vorführenden übernehmen.
Die Vorführung
Der Zuschauer hat die Karte Nr. 12 mit den Zahlen 1536 und 491 ausgesucht und Mag übergeben. Dieser gibt die beiden Zahlen bekannt.
Beim Nennen der ersten Zahl schreibt Mag diese über das Quadrat als die magische Summe, die das Quadrat haben wird.
Er gibt dem Zuschauer die Karte zurück und die Kreide dazu, mit der Bitte, die zweite Zahl in eine frei gewählte Zelle des Quadrates einzuschreiben.
Dieser trägt die 491 in die 3. Zelle der 2. Zeile ein.
Während der Zuschauer seiner Aufgabe nachkommt, dividiert Mag die magische Summe durch 2 und erhält 1536/2=768, von der er die zweite Zahl 491 abzieht und erhält 768-491=277.
Er übernimmt wieder die Kreide und trägt die 277 in die Zelle ein, die 2 Zellen in diagonaler Richtung zur vom Zuschauer eingetragenen Zahl ein. Das ist die 1. Zelle in der 4. Zeile. Es ist die Zelle 1 im Topquadrat und die 491 befindet sich in der Zelle 16. Diese Situation ist im Quadrat 1) dargestellt.
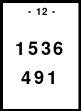
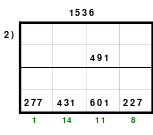
Die Kartennummer 12 verrät Mag, dass es sich um eine Zahlenkombination der Gruppe B handelt und der Übergang von den ersten 4 Zahlen zu den nächsten 4 Zahlen in der Doppelreihe nicht +/-50, sondern -/+230 ist und die vorgegebene Primzahl 491 ist die größte in der absteigenden Zahlenreihe.
Im Anschluss der in Zelle 1 eingetragenen 277 schreibt Mag in die folgenden Zellen der untersten Zeile unterschiedliche Primzahlen, die er errechnen muss.
Rechts neben der 1 ist im Topquadrat die 14. 14 gehört zum 4 Block wie auch die 491 in Zelle 16. 14 ist um 2 kleiner als 16. Deshalb zieht Mag 2*30=60 von 491 ab und schreibt in die Zelle 14 die Primzahl 431.
Die nächste Zelle ist die Zelle 11. die 11 gehört zum 3. Block, d. h. es erfolgt ein Übergang von Block 4 zu Block 3, der bekanntlich +230 ist. 11 ist um 5 keiner als 16. Da 1-mal der Übergang mit 230 bewertet wird verbleiben nur noch 5-1=4 Übergänge innerhalb des Blockes. Das bedeutet, von der 491 in Zelle 16 wird 4*30=120 abgezogen und 1*230 zugeschlagen. Das ist 491-120=371+230=601.
Die nächste Zelle ist die Zelle 8. Diese ist um 7 größer als 1 (Zelle 1). Die 8 gehört zum 2. Block. Es erfolgt auch hier ein Übergang von Block zu Block mit -230. Die Differenz 7 wird deshalb um 1 auf 6 reduziert. Die Primzahl für Zelle 8 wird folglich 277+6*30=277+180=457-230=227.
Dieses Zwischenergebnis zeigt das Quadrat 2).
Damit ist die Hauptarbeit erledigt. Die Berechnung der weiteren Zahlen für die noch offenen Zellen ist ein Leichtes. Sie werden ganz einfach von den Zahlen in der darüber befindlichen Zeile abgeleitet, denn dort sind immer Zahlen aus allen 4 Blöcken, die jeweils um +/-30 zu verändern sind. Dabei wird bedacht, dass die letzte Zeile im Beispiel die 1. Zeile im Topquadrat ist, also über der oberen Zeile die ja die 2, ist.
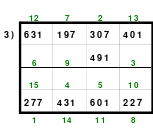
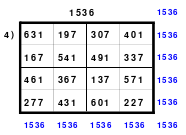
Die erste Zelle in der obersten Zeile ist die 12, eine Zahl des 3. Blockes, zu dem auch die Zahl in Zelle 11 zählt. Deshalb wird 601+30=631 in die Zelle 12 eingesetzt. Weiter mit Zelle 7, die um 1 kleiner als 8 ist, weshalb von 227 1*30 abgezogen werden muss und das Ergebnis 227-30= ist die Zahl für Zelle 7. Die nächste Zelle ist die Zelle 2, die 2. Zahl im 1. Block, weshalb dort 277+30=301 einzusetzen ist.
Weiter mit Zelle 13, in die 431 in Zelle 14 abzüglich 30=401 kommt. Dieser Zwischenstand ist im Quadrat 3) zu sehen. So wird Zeile um Zeile weitergearbeitet. So kommt in die Zelle 6, eine Zahl des 2. Blockes wie die 7, 197-30=167. In die Zelle 9, die zum 3.Block wie auch die 12 zählt wird 631-3*30=631-90=541 eingetragen.
So geht es weiter, Zelle um Zelle, bis das Quadrat 4) fertig ist. Es ist magisch und pandiagonal. Die magische Summe ist 1536, wie die anfangs über das Quadrat geschriebene Vorgabe.
Alle Zahlen sind Primzahlen und keine ist doppelt.
Mag war es gelungen, 15 weitere Primzahlen zu finden, in die eine vorgegebene Primzahl so eingeordnet werden konnte, dass ein magisches Quadrat entstand. Nicht nur alle Spalten, Zeilen und die beiden Diagonalen haben die gleiche magische Summe, sondern auch alle geteilten Diagonalen. Dabei durfte die magische Summe nicht irgendeine sein, sie musste einer vorgegebenen entsprechen. Eine unerklärliche Leistung!
(So kann man das auch sehen!)
Ein Non plus Ultra Quadrat kann bei 50% aller Karten erstellt werden und zwar immer, wenn eine Primzahl in Verbindung mit einer magischen Summe genannt ist.
In den anderen Fällen wird das Quadrat wie anfangs geschildert gebildet, wobei eine Primzahl vom Zuschauer in eine beliebige Zelle eingesetzt werden kann.
Mag schätzt zum Schluss dieses Abschnittes ein, dass diese Lösung leicht zu bewältigen ist und besser ist, als die vorangegangenen Experimente der Quadratbildung mit Primzahlen.
Die erarbeitete Lösung wird wahrscheinlich selbst für Kenner der Materie überraschend sein.
Eine Nachbetrachtung
Es war richtig dieses Experiment in das Hexen 1x1 aufzunehmen, auch wenn eine Wiederholung nicht ratsam ist.
Wer nicht auf die Möglichkeit einer Wiederholung verzichten will, muss ein sehr guter und schneller Rechner sein. Wiederholt sich die magische Summe, so ist auf der Karte die gleiche Kombination wie auf der vorherige. Das müssen wegen der unterschiedlichen Einordnung der Primzahlen bei der Gruppe A und Gruppe B nicht die gleichen Primzahlen sein.
Wird beim 2. Mal eine Karte der Gruppe B gewählt, ist der Vergleich der beiden magischen Summen schnell machbar. Das trifft aber nicht zu, wenn die 2. Karte eine aus der Gruppe A ist. In diesem Fall muss nämlich die magische Summe errechnet werden und das in höchstens 3 Sekunden.
Auch wenn die magischen Summen ungleich sind, besteht immer noch die Möglichkeit, dass eine der vorherigen Primzahlen in der veränderten magischen Summe zu finden ist. Dann werden 8 Primzahlen die gleichen sein, wie im vorherigen Quadrat. Dieses Risiko kann man noch eingehen.
Auf die Wahrscheinlichkeit einer Wiederholung von nur 10 bis 15%, sollte sich keiner einlassen. Denn ein gleiches Quadrat lässt den Verdacht aufkommen, dass das Ergebnis immer ein gleiches ist.
Ein paar Tipps (nicht nur für Anfänger)
Sie können auf eine Kartennummerierung verzichten und dafür die Karten farbig unterschiedlich gestalten. Aber bitte nicht nur in 2 Farben und diese nicht zu auffällig. An Hand der Farbe können Sie die Gruppe erkennen, zu der die Karte gehört und können auf eine Übergabe verzichten.
Um die Routine zu erleichtern, können Sie auch nur Karten der Gruppe A einsetzen, jedoch auch hier ohne die Karten 9, 23, 25 und 39, damit keine doppelten Zahlen auftreten können. Wenn noch die Karten mit der 1. Primzahl in Kombination mit der magischen Summe eingesetzt werden, ergeben sich immerhin noch 32 Karten. Das ist ausreichend für Darbietungen vor einem vertrauten kleinen Kreis von Zuschauern.
Der Übergang zum nächsten Block ist dann +/-50. Die Berechnung mit +/-230 entfällt.
Wem das Rückwärtsrechnen von der Zahl in Zelle 16 aus zu schwierig ist, der kann auch folgenden Weg gehen: Man zieht von der 2. Primzahl in Zelle 16 einfach 230 ab und setzt diese Zahl in die Zelle 9 ein. Die Zelle 9 befindet sich bekanntermaßen links neben der Zelle 16. Von dort werden dann in gewohnter Weise aufsteigend die Zahlen für die folgenden Zellen 10, 11, usw. mit +30 berechnet. Aber Achtung! Beim Übergang von Zelle 12 zur Zelle 13 muss +50 und nicht +30 gerechnet werden, denn das ist der Übergang zum nächsten Block.
(Die Zahl 230 ist die Differenz zwischen der 1. und letzten Zahl der Primzahlen- Doppelreihen, z. B. 271-41 oder 367-137.)
6.4. Quadrate der 5. Ordnung
6.4.1. Kleines Hexen 1x1
Das Pentaquadrat
Ein günstiges Quadrat der 5. Ordnung für das Hexen 1x1 ist das Pentaquadrat. Es ist ein Primquadrat, das nach der Springermethode erstellt ist. Die Zahlen (Zellen) sind in Blöcken von je 5 Zahlen eingeordnet (1-5, 6-10, 11-15, 16-20 und 21 -25).
In jeder Zeile, Spalte und den Diagonalen, auch in den gebrochenen Diagonalen befindet sich eine Zahl aus jedem Block. Des Weiteren sind diese Zahlen eine 1., 2., 3., 4. und 5. Zahl innerhalb ihrer Blöcke.
Die Sprünge innerhalb der Blöcke sind von Zahl zu Zahl 2 Zellen nach rechts und 1 Zelle nach unten. Dabei bilden die Zahlen eines Blockes eine in sich geschlossene Schleife. Wenn z. B. von der Zelle 1 viermal bis zur Zelle 5 gesprungen wurde, gelangt mit einem weiteren Sprung auf der Zelle 1.
Aber auch die Blöcke bilden eine solche Schleife. Ist die Zelle 25, die letzte im letzten Block, erreicht, kommt man mit einem weiteren Sprung zur Zelle 1, die zum 1. Block gehört.
Das Pentaquadrat ist ein pandiagonales. Jede Zelle (Zahl) kann jede Position im Quadrat einnehmen. Dabei bleibt die Ordnung erhalten.
Links das Pentaquadrat. Die magische Summe des Grundquadrates ist 65. Da es pandiagonal ist, können auch Spalten und/oder Zeilen versetzt werden, wobei das Quadrat ein magisches und pandiagonales bleibt.
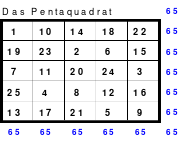
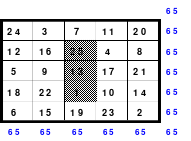
Das rechte Quadrat ist das Pentaquadrat nach Versetzen von 2 Spalten von hinten nach vorn und 2 Zeilen von oben nach unten. Dadurch ist die mittlere Zelle 13 in die Mitte des Quadrates gelangt. Interessant ist die darunter eingeordnete 1. Zelle und die darüber angeordnet Zelle 25, die größte.
Die mittlere Zelle ist die Zelle 13 und 13 ist 1/5 der magischen Summe 65. Zelle 1 plus Zelle 25 ergeben 26, das doppelte von 13 und bilden somit ein Duo.
All diese Eigenschaften werden bei Anwendung des Pentaquadrates in der Rechenkunst genutzt. Dabei werden andere Regeln angewandt als im kleinen Hexen 1x1 mit dem Topquadrat. Ein wesentlicher Grund ist, dass es nur schwer möglich ist, die Struktur der Zellenverteilung auswendig zu erlernen. Es ist möglich, aber schwer, die Regeln aus dem Topquadrat beim Pentaquadrat zu nutzen. Besonders der Start bringt oft Probleme mit sich. Das Springen wird beherrscht, aber die Übergänge erfordern eine hohe Konzentration. Um dieses Problem zu beherrschen, nutzt Mag die oben genannten Erkenntnisse aus der Analyse, gemischt mit den Kenntnissen aus der Arbeit mit dem Topquadrat.
Dazu folgen Beispiele mit kleinen Vorgaben zum besseren Verständnis.
Eine Zahlenvorgabe
Mag bittet um eine größere 2-stellige Zahl. Die Zahl muss mindestens 40 sein, damit von der Zahl in Zelle 13, die 3 als kleinste Schlüsselzahl, 13-mal abgezogen werden kann. Es wird 57 genannt.
Nun bittet die Zelle zu nennen, in die er die 57 einsetzen soll. Es wird die 2. Zelle in der 2. Zeile bestimmt, in die Mag die 57 einsetzt.
Es ist egal, welche Zelle genannt wird, für Mag ist es die Zell 13!
Mag multipliziert die 57 mit 5 und erhält 285, die er als magische Summe über das Quadrat schreibt. Rationell rechnet er 57*10, indem er gedanklich eine 0 anhängt und diese dann durch 2 dividiert (5 ist auch 10/2). Durch diese Manipulation werden die Ziffern des Ergebnisses von links nach rechts berechnet und so auch angeschrieben. (Quadrat 1)
Die Schlüsselzahl wird mit 57/13=4, berechnet und mit 3 gewählt.
Der mittlere Block mit der mittleren Zahl 57 wird komplettiert. Dazu werden nach 2 Rückwärtssprüngen die Zahlen 57-3=54 und 54-3=51 in die erreichten Zellen eingesetzt und nach 2 Vorwärtssprüngen in die Zahlen 57+3=60 und 6o+3=63. (Quadrat 2 - blau schattiert)
Diese Berechnung des mittleren Blockes muss als erstes erfolgen, denn diese Zahlen haben eine Informationsaufgabe bei der Berechnung der anderen Blöcke.
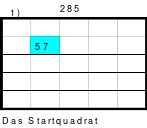
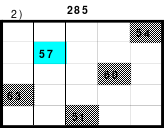
In die Zelle über der Vorgabe wird 2*57=114 eingesetzt. Das ist die Duosumme. In die Zelle unter der Vorgabe wird 0 geschrieben. (Quadrat 3).
Soll in die Zelle 1 eine Zahl eingesetzt werden, so muss die Zahl in Zelle 25 um diese reduziert werden. Denn beide Zahlen bilden ein Duo deren Duosumme 114 sein muss.
Ist die 0 eingeschrieben, wird sofort mit der Berechnung der Zahlen als aufsteigende Zahlenreihe mit der Differenz 3 begonnen und die Ergebnisse in die in Vorwärtssprüngen erreichten Zellen eingetragen. (Quadrat 4 - grün schattiert)
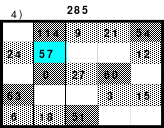
Dazu sind ein paar Bemerkungen sinnvoll. Sind von der 0 aus 4 Sprünge absolviert, so ist mit der Zahl 12 der 1. Block fertig. Ein weiterer Sprung ist nicht möglich, da dort die 0, die 1. Zahl im Block vorhanden ist. Deshalb geht es 2 Zellen nach unten mit der 15. Der nächste, der 2. Block, endet mit der Zahl 27. Von dort kann ebenfalls nicht weiter gesprungen werden, denn die Zielzelle ist mit der 15 belegt. Also 2 nach unten. Doch hier wird mit der 51 in der erreichten Zelle die Information gegeben, dass die aufsteigende Reihe fertig ist und mit der absteigenden Zahlenreihe begonnen werden kann. ausweicht.
Die Zahlen von 1 bis 16 werden in nur 2 Blöcke, 1 bis 8 und 9 bis 16, eingeteilt.
Nun muss geklärt werden, um welches Duo es sich bei den Vorgaben handelt.
Das Duo 1/16 kommt nicht infrage, da von der Zahl 36 nicht 7*7 = 49 für die Zahl in Zelle 9, die 1. im 2. Block, abgezogen werden kann.
Es wird gerechnet: Vorgabe 27 dividiert durch die Schlüsselzahl, das ist 27/7 = 3, Rest 6. Damit kann für die Zahl 27 die Zelle 4 des Grundquadrates festgelegt werden. Der Rest von 6 würde für die Zelle 1 verbleiben.
Da die Duosumme 17 ist, ergibt sich dann für die Vorgabe 36 die Zelle 13 des Grundquadrates. Das ist möglich, da von dieser 4*7 = 28 für die Zahl in Zelle 9, der 1. im Block 2 abgezogen werden kann. Anderenfalls müsste eine kleinere Schlüsselzahl gewählt werden.
Das 2. Quadrat der oberen Reihe ist dann das veränderte Topquadrat. Das muss man nicht extra erlernen. Man muss aber wissen, welche Zellen sich nebeneinander und
Im Gegensatz zur 0 als 1. Zahl im 1. Block ist die 114 die letzte Zahl im letzten, den 4. Block. Hier werden die Zahlen durch stetigen Abzug der Schlüsselzahl 3 berechnet und im Rückwärtssprung, 1 nach oben und 2 nach links, eingesetzt. Mit der Zahl 102 ist der 4. Block fertig und geh mit der 99 2 nach oben. Von dort weiter bis zur 87. Ein Rückwärtssprung führt zur mit 99 besetzten Zelle. Auch 2 nach oben geht nicht mehr, da hier die 63 aus dem mittleren Block informiert, dass auch die absteigende Reihe und damit das Quadrat, fertig sind. (Quadrat 5 - Rot schattiert)
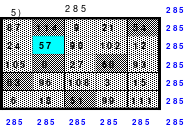
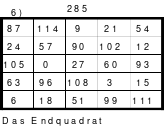
Das Quadrat 6 ist ohne farbige Orientierung, so wie es der Zuschauer sieht.
Es ist magisch und pandiagonal. Alle Zeilen, Spalten und die Diagonalen, auch die gebrochenen, haben die Summe 285, wie sie Mag als erste über das Quadrat geschrieben hat. Keine Zahl kommt doppelt vor.
Summenvorgabe
Die Berechnungen bei Vorgabe der magischen Summe sind die gleichen wie bei der Zahlenvorgabe. Allerdings muss vorher die Zahl für die Zelle 13 berechnet werden. Dazu wird die Vorgabe durch 5 geteilt, wobei meist ein Rest von maximal 4 auftreten kann. Dieser wird in die Zelle 1 eingesetzt.
Die Beschreibungen für das Beispiel kann kurzgefasst werden.
Mag bittet um eine 3-stellige Zahl aus dem oberen Bereich. Sie muss größer 455 rd. 500 sein, damit wenigstens mit der Schlüsselzahl 7 gerechnet werden kann.
Es wird die Zahl 638 genannt, die Mag als magische Summe über das Quadrat schreibt. Als Zelle für den Start ist die vorletzte in der 3. Zeile gewählt worden. Er teilt die 638 durch 5 und erhält 127 und einen Rest 3. Die 127 schreibt er in die vorgegebene Zelle, die für Mag die Zelle 13 ist. Der Rest 3 kommt in die Zelle 1. Ist kein Rest vorhanden, so muss von der später zu bildenden Zahl für Zelle 25 eine kleine Zahl für Zelle 1 abgezogen werden, oder man setzt einfach in die Zelle 1 eine 0 (Null) ein.
Nun läuft alles weitere wie bei der Zahlenvorgabe ab.
Die einzelnen Schritte sind:
Ermittlung der Schlüsselzahl mit 127/13 = 9,77, gewählt 9. (Eine einfachere Berechnung ist 1,2*8 = 9,6 >>> 9. (Die 12 passt rd. 8-mal in 100)
Berechnung und Eintragung der 2 auf- und 2 absteigenden Zahlen zur Komplettierung des mittleren Blockes.
Berechnung der Zahl für Zelle 25 durch Verdopplung der 127 zu 2*127=254. (Falls kein Rest vorhanden ist, kann z. B. die 254 auf 249 reduziert werden. Die abgezogene 5 wird in Zelle 1 eingesetzt. Im Beispiel besteht dazu kein Bedarf.)
Ausgehend von der 3 In Zelle 1 werden die aufsteigenden Zahlen berechnet und nach dem Springerprinzip eingesetzt. Aber Achtung: Der Rest darf nur einmal in jeder Reihe wirksam werden. Das wird bereits durch den Block 1 realisiert. Deshalb darf der Rest nicht mit in den 2. Block übernommen werden. Die Zahl für die Zelle 6 wird folglich 39+9-3=45 groß. Die nächsten Zellen werden wieder um jeweils 9 erhöht. (Siehe rote Schattierung)
Von der 254 in Zelle 25 aus, werden die absteigenden Zahlen berechnet und nach Rückwärtssprüngen eingetragen.
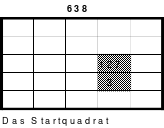
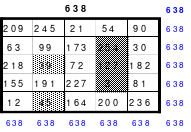
Das fertige Quadrat ist das rechte. Es ist magisch mit der vorgegebenen magischen Summe von 638. Die Zahlen sind gut gestreut und keine Zahl ist mehrfach vorhanden.
Eine kurze Nachbetrachtung
Mag schließt die Ausführungen zum “Kleinen Hexen 1x1” mit dem Pentaquadrat ab, mit der Meinung, dass die gezeigten Routinen eigentlich nicht mehr als klein bezeichnet werden können. Aufgrund der Größe des Pentaquadrates muss um größere Vorgaben als nur 2-stellige gebeten werden. Auch ist das Pentaquadrat wesentlich größer als das Lo-Shu- und Topquadrat.
6.4.2. Die “Hohe Schule” des Hexen 1x1
In der hohen Schule des Hexen 1x1 werden die zu bildenden Quadrate durch zeilenweise Eintragung der Zahlen erstellt. Das ist nicht so ohne weiteres machbar, denn das Erlernen der Zahlenfolge in einem Quadrat der 5. Ordnung ist kaum machbar, zumal eine derartige Vorführung nur selten möglich ist. Es galt folglich Lösungen zu finden, die diesen Weg nicht erforderlich machen, eine Lösung die man sich kurzfristig ins Gedächtnis rufen kann und die auf Logik aufbaut. Die Lösung hat Mag mit dem “Königsquadrat” gefunden. Auch wenn diese Lösung einfach ist, sind die erforderliche Rechenleistungen und besonders die erforderliche Konzentration doch erheblich und wird wahrscheinlich nur von Könnern beherrscht. Mag hat diesem Experiment deshalb auch 2 Sterne zuerkannt.
Um aber auch eine einfache, leicht zu realisierende Lösung zu finden, hat Mag die Variante “Einfach Clever” gestaltet. Sie ist einfach und ohne Schwierigkeiten machbar. Sie hat allerdings einen kleinen Schönheitsfehler. Es kann dabei zu doppelten Zahlen kommen, was normalerweise nicht sein soll. Deshalb ist diese Variante auch mehr für Laien und weniger für den Profi geeignet.
Allerdings ist die Möglichkeit doppelter Zahlen sehr gering. Die Wahrscheinlichkeit kann bei 2-stelligen Vorgaben mit rd. 1 zu 20 und bei 3-stelligen Vorgaben mit nur noch 1 zu 100 eingeschätzt werden. Maximal können nur 4 Zahlen doppelt sein.
Nach Fertigstellung des Quadrates sollte deshalb die Aussage: ”... und keine Zahl ist doppelt” unterlassen werden.
Sollte ein Zuschauer eventuell auf doppelte Zahlen aufmerksam machen, so erklären Sie einfach, dass dies durch die Vorgabe, die Sie ja nicht gemacht haben, begründet ist und übrigens das Quadrat 25 Zellen hat und nur 90 2-stellige Zahlen verfügbar sind. Bei diesem Gedränge können doppelte Zahlen nicht ganz ausgeschlossen werden. Deshalb mussten Sie z. T. auch auf 3-stellige Zahlen ausweichen.
Es gibt aber auch die Möglichkeit doppelte Zahlen auszuschließen, was allerdings eine zusätzliche Erschwernis durch die erforderlichen zusätzlichen Berechnungen zur Folge hat.
Die Rechenexperiment “Einfach Clever” hat Mag bereits im Abschnitt “Quadrate der 4. Ordnung” beschrieben. Aufgrund einiger Unterschiede bei der Anwendung eines Quadrates der 5. Ordnung, hat Mag die Ausführung vollständig gestaltet und sich nicht auf die Ausführungen zum Quadrat der 4. Ordnung bezogen.
Mag hofft, dass die beiden Experimente “Einfach Clever” und “Das Königsquadrat” Ihr Interesse finden.
6.4.3. Einfach Clever *
Die Grundvariante
Zahlenvorgabe
Auf der Tafel ist ein 5*5 = 25-zelliges Quadrat aufgezeichnet. Mag bittet einen Zuschauer um Nennung einer 2-stellige Zahl: Dieser nennt die Zahl 71, die Mag in die erste Zelle des Quadrates einschreibt. Sofort schreibt er über das Quadrat die Zahl 261 (linke Quadrate)
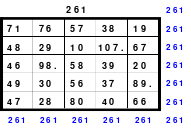
Anschließend füllt er zeilenweise alle Zellen des Quadrates mit Zahlen aus, wozu er keine 3 Minuten benötigt. Das fertige Quadrat ist magisch und pandiagonal, mit der magischen Summe von 261, die er vorher über das Quadrat geschrieben hat. Keine Zahl kommt doppelt vor. (rechtes Quadrat)
Die Lösung
Eine kurze Abhandlung was Mag wirklich macht:
Nach der Eintragung der Vorgabe 71 in die Zelle 1, addiert Mag zur Vorgabe die Primärzahl 190, das ist auch 200-10 und erhält so die magische Summe von 261, die er über das Quadrat schreibt. Anschließend schreibt er in die folgenden 4 Zellen die Zahlen 76, 57, 38 und 19. Diese Zahlen müssen Mag sich nicht merken, denn sie sind ganz leicht zu berechnen. Diese 4 Zahlen bezeichnet Mag als Flexzahlen.
(Sie ergeben sich aus 4*9+4*10=76, 3*9+3*10=57, 2*9+2*10=38 bis zur letzten Zahl in Zeile 1 mit 1*9+1*10=19 - warum, wird in der detaillierten Beschreibung erläutert.)
Damit ist die 1. Zeile fertig. Die Summe aller 5 Zahlen ergibt die magische Summe von 261, die Mag vorher über das Quadrat geschrieben hat.
Nun folgt die 2. Zeile, beginnend mit der 1. Zelle. Dazu geht Mag 1 Zelle nach oben und 2 nach rechts. Dort ist die Zahl 57, von der er 9 abzieht und das Ergebnis 48 in die 1. Zelle der 2. Zeile einschreibt. Dann folgt die nächste Zelle. Auch hier 1 nach oben und 2 nach rechts und von der 38 wird 9 abgezogen was 29 ergibt, die er einsetzt. (9 ist die festgelegte Schlüsselzahl).
So werden die Zahlen für alle weiteren Zellen berechnet und eingetragen.
Lediglich von der jeweils 1. Zahl im Block darf keine weitere 9 abgezogen werden, Hier muss 36 (4*9) zugezählt werden. Das ist bei der vorletzten Zelle in Zeile 2 der Fall. 1 nach oben, 2 nach rechts und man kommt auf die Zelle mit der Vorgabe und das ist ja die 1. Zahl im 1.Block. Von dieser darf nicht mehr die 9 abgezogen werden, sondern diese muss um 4*9=36 erhöht werden und die Zahl für die vorletzte Zelle in der 2. Zeile ist 71+36=107. Dies trifft auch auf die anderen 1. Zahlen der Blöcke zu. Diese erkennt Mag an der 0 als letzte Ziffer. Das ist z. B. in der 3. Zelle der 2. Zeile mit der Zahl 10 der Fall, weshalb in die erste Zelle der 3. Zeile nicht 10-9=1, sondern 10+36=46 einzusetzen ist.
Das fertige Quadrat ist pandiagonal mit der magischen Summe von 261 in jeder Spalte, Zeile und Diagonalen.
Auf einige, aber geringfügige Probleme wird später eingegangen.
Mag hat diese Handlungen der detaillierten Beschreibung vorangestellt, um zu zeigen, dass es sich um eine wirklich sehr leichte Lösung handelt. die ohne weiteres beherrscht werden kann und damit auch für Anfänger bestens geeignet ist.
Doch nun zu den Details der Lösung
Die Grundlage für dieses Experiment sind einmal das Pentaquadrat, ein Quadrat der 5. Ordnung und zum anderen ein alternatives “Das Clevere”. Das Clevere Pentaquadrat ist ebenfalls ein Springerquadrat, wobei die Sprünge innerhalb eines Blockes 2 nach rechts und 1 nach oben sind. Der Übergang von Block zu Block ist 2 nach oben.
Daraus ergibt sich die Situation, dass die vorangegangene Zahl, die ja um 1 größer ist, in der Regel durch 1 Zelle nach oben und 2 Zellen nach rechts zu finden ist. Eine Ausnahme der Regel wird durch die farbigen Zellen sichtbar. Hier sind die Zahlen nicht um 1 kleiner, sondern um 4 größer. Das muss so sein! Denn wie oft erwähnt bilden die einzelnen Blöcke in sich geschlossene Schleifen. Der obere rechts abgebildete Ring zeigt im Uhrzeigersinn eine aufsteigende Folge. Nach der 5 gelangt man wieder auf die 1. Linksherum folgt nach der 1 die 5. Im unteren Ring sind die Zahlen von Null beginnend jeweils um 9, die Schlüsselzahl, größer. Das bedeutet, dass nach der 1. Zahl im Block, die hier die Größe 0 hat, 36 folgt, dass 4-fache der Schlüsselzahl 9. (Siehe Abbildung rechts.)
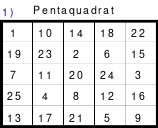
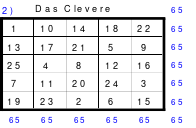
Damit ist die Berechnung der 2. bis 5. Zeile erklärt.
Die wichtigen Flexzahlen und die Primärzahl sind noch zu klären.
Dazu ist die grün schattierte Tabelle zu beachten.
Die erste Zeile der Tabelle enthält die Zellenzahlen der 1. Zeile des Alternativquadrates. Analysiert man diese Zahlen, so ist die Zahl 10 die 5. Zahl des 2. Blockes, die 14 die 4. des 3. Blockes usw. Diese Angaben für alle 5 Zahlen (1, 10, 14, 18 und 22 sind in Zeile b dargestellt. Die 5. Zahl im Block ist um 4 größer als die 1. Zahl des Blockes. Die 4. um 3 größer usw. Diese Zahlen nennt Mag Multizahlen, (Zeile c). Diese werden mit der Schlüsselzahl (Zeile d), im Beispiel die 9, multipliziert und man erhält so die Werte die dem Wert der 1. Zahl im Block zugeschlagen werden müssen (Zeile e). Nun müssen noch die Werte für die 1. Zahlen der Blöcke gefunden, bzw. bestimmt werden. Hier geht Mag den einfachsten Weg, indem er die zugehörigen Multizahlen mit dem Faktor (Zeile f) multipliziert. Diese Werte sind in Zeile g enthalten.
Die Faktoren haben in der Regel den Wert 10.
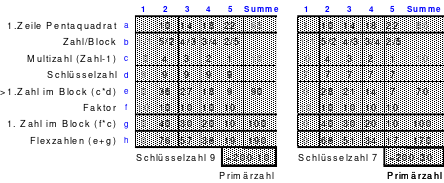
Durch die Multiplikation der Multizahlen mit 10 haben alle 1. Zahlen in den Blöcken als letzte Ziffer eine Null und können dadurch wie vorn beschrieben leicht erkannt werden. Werden die Zahlen der Zeilen e und g addiert, so erhält man die Flexzahlen in Zeile h, die in das zu berechnende Quadrat übernommen werden.
Die einfache Berechnung der Flexzahlen kann schnell erfolgen, weshalb diese nicht gemerkt werden müssen. Allerdings müssen die Multizahlen erlernt sein, was ziemlich leicht ist. Denn diese beginnen mit der 4 und enden nach Abzug von 1 zur letzten Multizahl 1.
Die sehr kleine Pause die bei der jeweiligen Berechnung entsteht ist gewollt, weil sie so dem Zeitaufwand zu den Berechnungen der übrigen Zellenzahlen entspricht.
Die Addition der 4 Flexzahlen aus den Spalten 2 bis 5 ergibt die Summe von 190, was auch 200-10 ist. Diese Zahl ist die Primärzahl mit deren Hilfe die magische Summe berechnet wird, indem dieser die Vorgabe zuaddiert wird. Das ist im Beispiel 190+71=261.
Die Summe der 4 Multizahlen ist 10. Daraus abgeleitet ist der Anteil der Schlüsselzahlen in der Primärzahl das 10-fache der Schlüsselzahl. Bei der Schlüsselzahl 9 ist das 9*10=90, was die letzten Ziffern der Primärzahl sind. Da der Grundfaktor 10 ist, ergibt sich, dass dieser mit 10*10=100 in die Primärzahl eingeht. So kann die Primärzahl ganz leicht berechnet werden. Bei Einsatz der Schlüsselzahl 7 ist das 170 und bei einer Schlüsselzahl 19 = 290.
Sollten in der Berechnung noch Unklarheiten bestehen, empfiehlt Mag den Abschnitt “Eine kurze Abhandlung was Mag wirklich macht” nochmals auszuwerten.
Leider ist diese einfache Lösung nicht ganz ohne Probleme. Mag beschreibt diese und zeigt dazu Lösungswege in den Ergänzungsvarianten.
1. Ergänzungsvariante
Eines der Probleme ist die Möglichkeit, dass doppelte Zahlen vorkommen können, was nur durch eine ungünstige Vorgabe entstehen kann und eine Verhinderung fast unmöglich ist, da zur Prüfung umfangreiche Berechnungen notwendig sind.
Diese Möglichkeit kann aber ausgeschaltet werden. Doppelte Zahlen können nicht auftreten, wenn die Vorgabe größer als die Flexzahl in Spalte 2 mit der Multizahl 4 ist. Dieser Wert ist der größtmögliche. von dem 4-mal die Schlüsselzahl abgezogen wird. Ist die Vorgabe größer, sind doppelte Zahlen nicht möglich, denn die Vorgabe kann keinen kleineren Wert annehmen, da bereits in der 2. Zeile dieser um das 4-fache der Schlüsselzahl erhöht wird. Es gilt deshalb, die Flexzahl kleiner als die Vorgabe zu bilden. Die Möglichkeiten sind:
1. Man bittet um eine 2-stellige Zahl im oberen Bereich. Das bringt nur eine Lösung, wenn eine Zahl größer 76 genannt wird. (genauer 68 bei der Schlüsselzahl 9)
2. Wenn die Vorgabe kleiner ist, muss eben die Flexzahl verkleinert werden. Das wird erreicht durch Einsatz einer kleineren Schlüsselzahl. Bei Einsatz der Schlüsselzahl 7 wird die größte Flexzahl = 68. Als nächstes kann der Grundfaktor mit 1 bestimmt werden. Hier wird die Flexzahl weiter auf nur noch 4*7+4*1= 32 gesenkt. Die Primärzahl wird dann 7*10+1*10=80 groß.
Die Differenzen zwischen den Zahlen innerhalb eines Blockes ist 7.
Achtung: Da jetzt die 1. Zahl im Block nicht durch Multiplikation der Multizahl mit 10, sondern mit 1 erfolgt, werden diese nur einstellig. Sie sind nicht mehr an der 0 als letzte Ziffer erkennbar, sondern als 1-stellige Zahl von 1 bis 4.
2. Ergänzungsvariante
Ein weiteres Problem ist die Erhöhung bei Erreichung der Null als Endziffer (oder 1-stellige Zahl) bei der 36 oder bei der Schlüsselzahl 7 nur 28 zugezählt werden muss. Es kann passieren, dass im 1. Block, der mit der Vorgabe beginnt, ein Zwischenergebnis mit einer Endziffer Null vorkommt, der natürlich nicht um 36 bzw. 28 erhöht werden darf. Um Irrtümer auszuschließen hat Mag die Zahlen des 1. Blockes, die mit der Vorgabe beginnen, durch einen Punkt kenntlich gemacht. Das kann auch durch eine weniger auffallende Kennzeichnung erfolgen, welche, bleibt Ihnen überlassen.
3. Ergänzungsvariante
Kein Problem ist eine Wiederholung. Sie darf nur nicht mit den gleichen Flexzahlen erfolgen, denn dann würden 20 Zahlen die gleichen sein, wie in der vorangegangenen Quadratbildung.
Es können 2 Wege gewählt werden, um eine Veränderung der Flexzahlen zu erreichen.
1. Man wählt eine andere Schlüsselzahl. Das kann 3, 7, 13, 19 oder auch 109 sein. Die Primärzahl ändert sich dabei zu 130, 170, 230, 290 oder 2090. In allen Fällen können sie einfach berechnet werden und müssen nicht durch Addition der Flexzahlen ermittelt werden.
2. Es können die Flexzahlen nach deren Berechnung einheitlich um eine beliebige Zahl erhöht werden. Die Primärzahl muss dann um das 4-fache dieser Zahl erhöht werden. Günstig wäre z. B. die 3. Die Primärzahl würde dann 190+4*3=202, das ist auch 200+2. Die Erweiterung kann natürlich auch 2-stellig sein.
Beachten Sie aber folgende Änderung:
Die Endziffern der Zuschläge sind jetzt die Erkennung der 1. Zahlen der Blöcke, bei denen nicht die Schlüsselzahl abgezogen wird, sondern um 36 oder 28 erhöht werden müssen.
4. Ergänzungsvariante
Da bei der Vorgabe einer Zahl kein Rest entsteht, sollte die Zelle des Anfangs von den Zuschauern bestimmt werden. Meistens wird eine Zelle im Inneren des Quadrates genannt, in die die Vorgabe eingesetzt wird. Die Flexzahlen werden hinter der Vorgabe beginnend eingetragen, wobei auch Flexzahlen links von der Vorgabe eingeordnet werden.
Das hat den Vorteil, dass die Flexzahlen nicht so schnell als absteigende Zahlenreihe erkannt wird.
(Die Zellenvorgabe sollte fester Bestandteil der Vorführung werden. Es wird dadurch auch eine erhöhte Schwierigkeit vorgetäuscht.)
Vorgabe der magischen Summe *
Nach dieser Methode ist auch die Erstellung eines magischen Quadrates bei Vorgabe der magischen Summe möglich. In diesem Fall erfolgt die Berechnung im umgekehrten Sinn, d. h. von der Vorgabe wird die Primärzahl abgezogen und man erhält die Zahl für die Zelle 1. Die weiteren Berechnungen erfolgen dann wie bisher bei Vorgabe einer Zahl für Zelle 1.
Allerdings ist die Bildung eines magischen Quadrates bei Vorgabe der magischen Summe schwerer zu lösen als dies bei der Vorgabe einer Zahl für Zelle 1 ist. Mag wird anhand eines Beispiels das zusätzliche Problem sichtbar machen.
Er hat aber auch Wege gefunden, um dieses Problem zu beherrschen. Diese Lösungen sind jedoch schwerer zu realisieren, weshalb Mag den Rat gibt, auf die Lösung entsprechend dem “Kleinen Hexen 1x1”, oder dem “Königsquadrat“
auszuweichen. Das gilt besonders für 4-stellige Vorgaben die nicht mit einer Schlüsselzahl von nur 9 oder 7 erstellt werden sollten, da die Streuung der Zahlen völlig unbefriedigend ist. 3-stellige Vorgaben sollten möglichst auf die Schlüsselzahl 9 beschränkt werden. Nun ein Beispiel.
3-stellige Vorgaben
Mag hat um eine 3-stellige Vorgabe größer 300, gebeten.
(Größer 300 deshalb, da nach Abzug der Primärzahl von 190 eine positive Zahl für Zelle 1 übrigbleiben muss!)
Nachfolgend ein Beispiel mit der Vorgabe der 3-stelligen magischen Summe von 978. Die Berechnung erfolgte mit der Schlüsselzahl 9 und einer Primärzahl von 190.
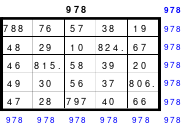
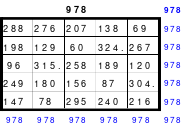
Zum linken Quadrat
Mag hat von 978 erst 200 abgezogen und dann um 10 erhöht, das ist eine Reduzierung um 190 was der Primärzahl entspricht und damit 978-200=778+10=788 erhalten, die in die Zelle 1 eingesetzt wurde.
Alle weiteren Schritte erfolgen in der bekannten Weise.
Auch hier wurden alle Zahlen des 1. Blockes mit einem Punkt versehen.
Das entstandene Quadrat ist magisch mit der magischen Summe von 978, was der Vorgabe entspricht. Es ist auch pandiagonal.
Allerdings gibt es hier neben den bereits genannten Problemen ein weiteres, das mit der Vorgabe von 978 kenntlich gemacht wird.
Es ist auffallend, dass vorwiegend nur 2-stelligen Zahlen und 3-stellige Zahlen größer 700 im Quadrat vorhanden sind, was durch die hohe Vorgabe bedingt ist.
Zum rechten Quadrat
Um die großen Zahlen zu reduzieren, müssen die übrigen Zahlen logischerweise vergrößert werden. Das ist möglich durch Erhöhung des Faktors der ja durch Multiplikation mit der Multizahl zu einer größeren ersten Zahl im Block und damit auch aller anderen Zahlen des Blockes führt. Gleichzeitig wird die Primärzahl erhöht, wodurch die Zahl für Zelle 1 kleiner wird.
Die Erhöhung des Faktors erfolgt dabei in 10er Schritten. Das sind jeweils 100, um die sich die Primärzahl erhöht und 40, um die sich die größte Flexzahl vergrößert. Das ist zusammen 140. Mit jeder Erhöhung des Faktors um 10 wird die Differenz zwischen der Vorgabe und Primärzahl um 140 reduziert. Gleichzeitig erhöht sich die große Flexzahl um 4*10=40.
Nach diesen Regeln wird für das Beispiel eine Neuberechnung erstellt.
Um das Rechnen zu erleichtern, werden alle in die Berechnung eingehenden Zahlen um die letzte Ziffer gekürzt.
Als erstes wird die Differenz zwischen der Vorgabe und der Primärzahl gebildet. Im Beispiel ist das 97-19=78. Diese wird durch 14 geteilt und ergibt 5, der Rest wird nicht weiter beachtet. Der Faktor ist somit um 5*10=50 auf 60 zu erhöhen.
Die Ergebnisse sind in der Tabelle zu erkennen.
Die Flexzahlen sind 276, 207, 138 und 69 und die Primärzahl ist 690.
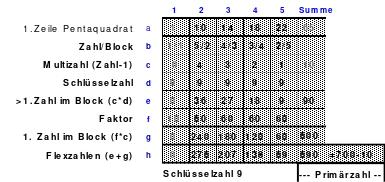
Das mit den neuen Werten berechnete Quadrat ist das rechte. Die Zahl für Zelle 1 ergab sich durch 978-690 = 288.
Es ist magisch und pandiagonal mit der magischen Summe von 978.
Die einzelnen Zahlen haben keine auffallenden Differenzen zueinander und nicht doppelt vorhanden.
Eine Nachbetrachtung
Mag hat bei seinen Beispielen die Schlüsselzahl 9 eingesetzt. Auch andere Schlüsselzahlen können eingesetzt werden. Das Grundprinzip ist das gleiche.
Nach diesem Prinzip können sogar Quadrate mit 4-stelligen Vorgaben gebildet werden.
Allerdings können die bisherigen Werte für Schlüsselzahlen und Faktoren nicht mehr genutzt werden. Auch diese müssen erhöht werden.
Eine Schlüsselzahl von 109 und ein Faktor 100 könnten zum Einsatz kommen.
Die Zahlenvorgabe sollte größer 800 (1000) und die Summenvorgabe größer 3000 sein.
Die Tabelle zeigt die zum Einsatz kommenden Flexzahlen und die Primärzahl.
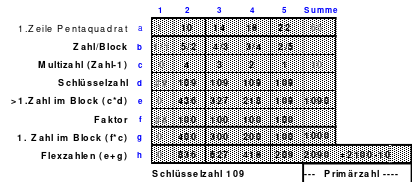
Auch wenn das Rechnen mit der Schlüsselzahl 109 und einem Faktor 100 fast genau so leicht ist wie mit einer Schlüsselzahl 9 und einem Faktor 10, wird die Umsetzung der größeren Zahlen nicht mehr ganz so leicht von der Hand gehen. Man sollte es sich deshalb gründlich überlegen die höhere Variante in sein Programm aufzunehmen. Mag hat es bei der kleinen Variante belassen.
Mit diesen Hinweisen schließt Mag seine Ausführungen zu “Einfach Clevere” ab.
In der weiteren Folge wird er das “Königsquadrat” beschreiben, dass nicht nur eine höhere Qualität hat, sondern auch viel schwieriger in der Anwendung ist, weshalb es auch 2 Sterne erhalten hat.
6.4.4. Das 5er Königsquadrat * * (Ein Experiment der hohen Schule)
Vorführungen von Rechenkunst-Experimenten mit einem magischen Quadrat der 5. Ordnung sind natürlich schwerer als die Arbeit mit Quadraten der 3. oder 4. Ordnung. Entscheidend ist u. a. die Tatsache, dass hier 25 Zellen mit Zahlen ausgefüllt werden müssen, was bedeutend länger dauert. Nur durch sehr schnelles Arbeiten kann hier das Aufkommen von Langeweile und Desinteresse vermieten werden. Ein weiteres Problem ist die Tatsache, dass es sehr schwer sein wird, die Zellenfolge des Quadrates auswendig zu erlernen. Da die Berechnungen ähnlich wie bei dem Quadrat der 3. Ordnung sind, ist die Bildung der Schlüsselzahl und die Erhöhung von bereits errechneten Zahlen um bis zum 6-fachen der Schlüsselzahl wesentlich schwieriger als beim Quadrat der 3.Ordnung. Dafür ist die Vorführung aber wesentlich spektakulärer. Mag hat rationelle Lösungen gefunden, die eine Vorführung mit einem Quadrat der 5. Ordnung erleichtern.
Dazu hat Mag das Königsquadrat, ein Springerquadrat der 5. Ordnung, gebildet und analysiert. Nachstehendes Quadrat der 5.Ordnung ist ein pandiagonales Springerquadrat mit den Zellen 1 bis 25.
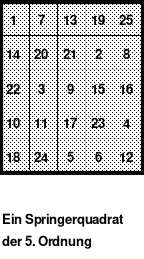
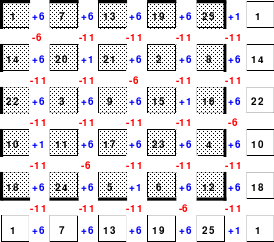
Die Analyse dieses Quadrates ergab, dass es nach bestimmten Regeln aufgebaut ist. Diese sind:
In der Zeile ist die folgende Zellenzahl um 6 größer. Außer bei Zellenzahlen, die durch 5 teilbar sind (5, 10, 15, 20 und 25). Hier ist die folgende Zellenzahl nur um 1 größer.
Die erste Zellenzahl der folgenden Zeile ist um 11 kleiner als die letzte Zellenzahl der vorhergehenden Zeile. Außer bei Zellenzahlen, die nach Abzug von 1 durch 5 teilbar sind (1, 6, 11, 16 und 21). Hier ist die erste Zahl der folgenden Zeile nur um 6 kleiner.
In allen Fällen gilt: Ist die errechnete Zellenzahl größer 25, so muss 25 abgezogen werden. Ist sie kleiner 1, so muss 25 zugezählt werden.
Analog muss auch von der berechneten Zahl das 25-fache der Schlüsselzahl abgezogen bzw. zugerechnet werden.
Diese Regeln sind leicht zu merken und ermöglichen die Berechnung der jeweils folgenden Zellenzahl, egal wo begonnen wird.
Von großem Vorteil ist, dass das Springerquadrat ein pandiagonales ist. Dadurch kann z.B. die Zelle 13 durch Versetzen von Zeilen und/oder Spalten an jede beliebige Stelle versetzt werden.
Nachfolgend werden 2 erprobte Varianten der Rechenkunst mit einem magischen Quadrat der 5. Ordnung und 4- bzw. 5-stelligen Vorgaben beschrieben.
Aufgrund der großen Vorgaben sind diese Experimente zusätzlich dem “Großen Hexen 1x1” zuzuordnen.
Mag will hier zeigen, dass auch mit großen Zahlen leicht gerechnet werden kann.
Dabei handelt es sich um Beispiele, die der Akteur je nach Können einschränken oder erweitern kann.
Variante 1 - Zellenvorgabe
Der Vorführende (künftig kurz Mag) bittet 3 Zuschauer als Jury seine Arbeit zu überprüfen. Einer soll die Zahlen einer beliebigen Zeile, ein Weiterer die einer Spalte und der Dritte die einer Diagonale addieren. Zur besseren Lösung dieser Aufgaben stellt Mag Taschenrechner zur Verfügung.
(Nur wenn keiner ein Smartphon besitzt.)
Mag bittet die Zuschauer um Nennung der Zelle, mit der er beginnen soll. Dann bittet er um die Nennung einer 4-stelligen Zahl.
Die Zuschauer nennen als Zahl 2761 und als erste Zelle die 4. in der 3. Zeile, in die Mag die Zahl 2761 einschreibt (nur hier grün markiert).
Sofort schreibt Mag über das Quadrat die Zahl 13805.
Danach setzt Mag in die nächste Zelle (die 5. in der 3. Zeile) die Zahl 3955 ein. Dann weiter mit der 1. Zelle in der 4. Zeile, in die er die Zahl 1766 schreibt.
Auch in die folgenden Zellen setzt er Zahlen ein. Nach der Zelle 5 in der 5. Zeile geht es weiter mit Zelle 1 in der 1. Zeile.
Nach dem Mag alle Zellen mit Zahlen versehen hat, weist er darauf hin, dass keine Zahl doppelt vorhanden ist und alle Zeilen, Spalten und die beiden Diagonalen die gleichen Summen von 13805 haben, die er zu Beginn über das Quadrat geschrieben hat. Damit ist das Quadrat ein magisches. (Sogar ein pandiagonales)
Die Richtigkeit dieser Aussage wird von der Jury bestätigt.
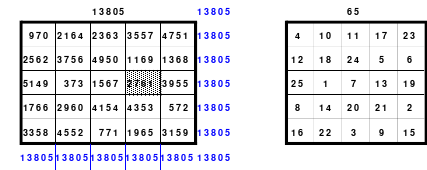
Die Lösung entspricht dem Verfahren wie beim Quadrat der 3. Ordnung. Dabei ist vom Vorteil, dass es sich beim Quadrat der 5. Ordnung um ein pandiagonales Quadrat handelt. Egal in welche Zelle die Vorgabe eingesetzt wird, für Mag ist es die Zelle 13. Das vorn gezeigte Quadrat hat sich in das Quadrat rechts verändert. Es bleibt ein pandiagonales magisches Quadrat mit der magischen Summe von 65.
Ein wichtiger Aspekt ist, dass die magische Summe von 65 das 5-fache von 13, der mittleren Zellenzahl, ist. Mag hat also nur die Vorgabe mit 5 multipliziert und über das Quadrat als künftige magische Summe geschrieben. Natürlich hat Mag die Multiplikation rationeller gelöst. Da 5 auch 10/2 ist, hat er die Vorgabe gedanklich durch anhängen einer Null mit 10 multipliziert und dann durch 2 dividiert. Durch diesen kleinen Trick wird die Zahl der magischen Summe zwangsweise von links nach rechts gebildet und so auch angeschrieben.
Als nächstes wird die Schlüsselzahl gebildet. Da die mittlere Zellenzahl 13 um 12 größer ist als die Zellenzahl 1, muss die Schlüsselzahl kleiner 1/12 der Vorgabe sein, das ist im Beispiel 2761: 12 = > 200. Mag hat hier die Schlüsselzahl mit 199, das ist auch (200 - 1) festgelegt.
Nun kann mit dem Einsetzen der Zahlen in die folgenden Zellen begonnen werden.
Da die 13 nicht durch 5 teilbar ist, ist die folgende Zellenzahl um 6 größer, folglich 13 + 6 = 19. In diese Zelle setzt Mag die Zahl aus Vorgabe plus das 6-fache der Schlüsselzahl, das ist 2761 + (200 - 1) x 6 = 2761 + 1200 - 6 = 3955 ein. Die um 1 reduzierte Zellenzahl 19 ist nicht durch 5 teilbar. Deshalb ist die Zellenzahl der 1. Zelle in der folgenden Zeile um 11 kleiner als 19, also Zelle 8. Die Zahl für diese Zelle ist um das 11-fache kleiner als die Zahl in Zelle 19. Es muss von dieser 11 x (200 - 1) abgezogen werden. Einfach dargestellt 3955 - 2200 + 11. Man zieht einfach 22 von 39 ab und erhält die ersten 2 Ziffern mit 17. Dann wird 55 um 11 auf 66 erhöht und die letzten beiden Ziffern sind gefunden. In der Zelle 8 steht nun die Zahl 1766. Aber Achtung! Auch hier gilt es zu prüfen ob das so einfach geht. Gegebenenfalls müssen vordere Ziffern um +/-1 erhöht oder vermindert werden.
Damit dürfte alles gesagt sein und weitere Erläuterungen sind nicht erforderlich.
Selbstverständlich ist es auch möglich die Vorgabe des Zuschauers auf eine 3-stellige Zahl zu reduzieren. Allerdings muss dann eine entsprechend kleinere Schlüsselzahl gewählt werden.
Variante 2 - Summenvorgabe
Mag lässt sich eine 4-stellige Zahl größer 6000, besser eine 5-stellige Zahl, nennen, die er sofort über das Quadrate schreibt. Eine Vorgabe kleiner 6000 hätte eine 2-stellige Schlüsselzahl und damit ein schwierigeres Rechnen zur Folge. Im Beispiel wird die Zahl 73843 genannt.
Des Weiteren bittet er um Nennung der Zelle in die er die erste Zahl schreiben soll. Die Zuschauer nennen die 2. Zelle in der 2. Zeile. In diese setzt Mag die Zahl 14768 ein. Die gewählte Zelle ist für Mag die Zelle 13. Das Quadrat der 5. Ordnung ist damit zu dem rechts abgebildeten umgestellt. (nächste Seite)
Die Zahl für die Zelle 13 hat Mag durch Division der Vorgabesumme durch 5 ermittelt. Da eine Division von vorn nach hinten gerechnet wird, kann das Ergebnis ebenfalls von links nach rechts geschrieben werden. Im Allgemeinen bleibt dabei ein Rest, der aber stets kleiner 5 ist. Im Beispiel ist es 3.
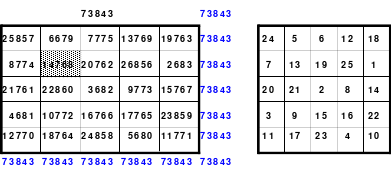
Der weitere Ablauf ist wie in Variante 1 beschrieben. Die Schlüsselzahl wird durch Division der Zahl in Zelle 13 durch 12 ermittelt. Im Beispiel hat Mag als Schlüsselzahl 999, das ist (1000 - 1) gewählt.
In die folgende Zelle, die 19, wird nun die um 6 x 999 erhöhte Zahl eingesetzt. Mag erhöht ganz einfach 14 um 6 und hat damit die ersten beiden Ziffern bereits ermittelt, die er auch gleich einschreibt.
Von der letzten Ziffer 8 zieht er 6 ab und kann so die begonnene Zahl mit 762 zur Gesamtzahl 20762 ergänzen.
Alles Weitere wird wie bekannt abgearbeitet. Allerdings muss der Rest von 3 noch den Zellen eines Blockes zugeschlagen werden. Mag hat die Zahlen für die Zellen 1 bis 5 um den Restbetrag erhöht. Da in jeder Zeile, Spalte und Diagonalen jeweils nur eine Zahl eines Blockes zu finden ist. werden alle Zeilen, Spalten Diagonalen um den Rest erhöht und so die magische Summe sichergestellt. Der Rest kann auch den Zahlen für den letzten Block, 21 bis 25, oder dem 2. Block, 6 bis 10, zugeschlagen werden. Nicht geeignet ist der 3. Block mit den Zellen 11 bis 15, da sich in diesem die Zelle 13 befindet.
Mag schließt seine Darlegungen zur “Hohen Schule” mit dem Königsquadrat ab und hofft, dass Sie auch die Prinzipien des Rechnens mit dem Königsquadrat erkannt haben und eventuell sogar nutzen können. Dabei können Sie selbstverständlich auch um kleinere Vorgaben bitten.
Eine Nachbetrachtung
Mag hat bei den Erläuterungen zum Königsquadrat sehr große Zahlen als Vorgaben gewählt, was auch entsprechend große Schlüsselzahlen erforderte.
Damit hat er seine Gepflogenheiten, kleine Zahlen für ein besseres Verständnis zu verwenden, verlassen. Das liegt daran, dass diese Ausführungen bereits vor Jahren entstanden sind. Er hat von einer Überarbeitung Abstand genommen, um zu zeigen, dass auch mit großen Zahlen rationell gerechnet werden kann.
Mag ist der Meinung, dass die Berechnungen beim Königsquadrat vorteilhafter mit großen Vorgaben sind. Durch die getrennte Berechnung der Hunderter und den 2-stelligen Rest werden zwar für jede Zahl 2 Berechnungen erforderlich, diese werden aber mit entschieden kleineren Zahlen berechnet. Das ist wesentlich leichter ist und erfordert kaum einen höheren Zeitaufwand.
Bei der 5-stelligen Summenvorgabe wurde die Zahl in Zelle 13 ebenfalls 5-stellig. Als Schlüsselzahl wurde 999 (1000-1) festgelegt. Um auch hier günstig zu rechnen, wurde die Zahl in Zelle 13 in eine Tausenderzahl und eine restliche 3-stellige Zahl geteilt. Die Tausenderzahl wurde u. a. um jeweils 6 erhöht und der Rest um 6 gekürzt.
In den Beispielen waren die Zahlen, die zur vorherigen addiert oder subtrahiert werden mussten 1*6=6, 1*11=11 und 2*6=12, sowie 2*11=22.
Bei kleineren Vorgaben werden Schlüsselzahlen von 9, 19, 29 usw. erforderlich. Das bedeutet, dass das 6- und 11-fachen dieser Schlüsselzahlen Größen von 54 bis 319 und noch größer zur Folge haben, mit denen nicht so leicht gerechnet werden kann. (Zumindest nicht schnell genug.)
Für die von Mag bevorzugte Variante sind Schlüsselzahlen der Größe 97-103,197 - 203 und 297 - 303 günstig. Die möglichen Vorgaben für Zelle 13 würden die Größen von rd. 1200 bis 3600 erfordern und für die Summenvorgaben 6000 bis 18000.
Die Schlüsselzahl 3
Natürlich ist es am einfachsten, die 3 als Schlüsselzahl zu wählen und die Vorgabe einer Zahl, auf eine größere 2-stellige (>40) zu beschränken. Die Vorgabe für die Summe sollte eine Zahl aus der 200er Reihe sein (>200). Diese Werte sind das Minimum. Die Vorgaben können auch ein Mehrfaches der Angaben sein, was lediglich eine größere Zahl für Zelle 1 zur Folge hat.
Mit einer 3 zu rechnen erfordert nur eine Berechnung statt zwei, wie bei großen Zahlen und die 3 ist auch eine kleine Zahl mit der leicht zu rechnen ist.
Zu beachten ist jedoch, dass der Rest gleich oder größer als die Schlüsselzahl sein kann und dann nicht den Zahlen des 1. Blockes zugeschlagen werden darf. Der Rest sollte bei einer 3 als Schlüsselzahl den Zahlen des letzten Blockes zugerechnet werden. Das sind die Zahlen 42 bis 49. Nachteilig ist, dass diese Zahlen nicht wie üblich hintereinander erreicht und berechnet werden können.
Die 3 als ungünstige Schlüsselzahl zu bewerten, weil die Zuschauer die Erhöhung bzw. Verminderung der Zahlen um 3 leicht erkennen können, gilt hier nicht, denn die folgende Zahl ist ja bei einer Schlüsselzahl 3 um 6*3=18 größer und bei Zeilenwechsel um 11*3=33 kleiner. Nur 7-mal wird die Folgezahl um 3 erhöht.
Der Zuschauer wird keine Veränderung um jeweils 3 erkennen können. Dazu müssten alle Zahlen verglichen werden. Er hat aber dazu kaum Zeit, weil Sie inzwischen zum nächsten Experiment übergegangen sind oder Ihre Darbietung beendet haben.
Zusammenfassend kann gesagt werden, dass dieses Rechenkunststück mit zu den schwierigsten zählt, das Mag Ihnen zumutet, jedoch nicht so schwierig, dass es unmöglich ist, es zu beherrschen. Wenn Mag dieses Experiment selbst nicht öffentlich vorgeführt hat, so hat er es aber im Selbsttest geprüft. Dabei hat er es fehlerfrei in ca. 12 Minute geschafft, was natürlich viel zu lange ist. Wer dieses Rechenkunststück vorführen will, muss es in weniger als 5 Minuten schaffen.
Aber bedenken Sie auch hier, dass Masse nicht mit Klasse verwechselt werden sollte. Es genügt vollkommen das Quadrat mit der Schlüsselzahl 3 zu gestalten. Der Zuschauer kann Ihre Darbietung besser verfolgen und auch mal rechnerisch überprüfen.
6.4.5. 5er Primzahlenquadrate *
Die 6-fache Vorgabe
Mag überlegte, ob es nicht doch möglich ist, ein 5er Primzahlenquadrat so zu gestalten, dass eine Vorführung wie mit dem 4er Topquadrat erfolgen kann. Er hat eine Lösung gefunden, die aber leider weniger attraktiv ist. Eine Lösung ist auch hier nur mittels Karten mit vorgegebenen Primzahlen möglich. Leider waren keine Primzahlenreihen mit 10 Zahlen zu finden, weshalb keine Blöcke zusammengefügt werden können. Es mussten Primzahlenreihen mit 5 Zahlen zum Einsatz kommen. Das bedeutet, dass neben der magischen Summe insgesamt 5 Primzahlen dem Vorführenden genannt werden müssen. Beim Topquadrat waren es neben der magischen Summe nur 2. Eine Vorführung mittels einer einfachen Springervariante ist nicht besonders geeignet, da die Lösung leicht erkennbar ist. Mag hat deshalb zwei halbwegs brauchbare Wege erarbeitet, mit denen eine Vorführung gewagt werden kann. In beiden Varianten ist die Berechnung einfach, erfordert aber eine hohe Konzentration. Trotz aller genannten Probleme hat Mag dieses Experiment in seine Ausführungen aufgenommen. In einer 3. Variante nutzt Mag alle bisher gewonnenen Erkenntnisse zur Gestaltung des Primzahlenquadrates “Varianten-Kombi”.
Variante 1 - “Halb gesprungen”
Auf der Tafel ist ein leeres Quadrat der 5. Ordnung abgebildet. Mit den Worten: ”Da es schwer ist, viele Primzahlen im Kopf zu behalten, habe ich diese Karten angefertigt. Auf denen sind in unterschiedlicher Anordnungen Primzahlen zu finden.”
Dazu zeigt er von 30 Karten einige und verweist auf die unterschiedlichen Primzahlen auf diesen.
Dann bittet er einen Gast um Mitwirkung bei diesem Experiment. Der Gast soll eine Karte auswählen und anschließend die große Zahl auf dieser nennen. Der Gast sagt die Zahl 1625, die Mag über das Quadrat schreibt. Dann bittet er um Nennung einer der kleineren Zahlen. Es wird 11 genannt, die Mag in ein Feld des Quadrates einsetzt. Dann folgen die Zahlen 137, 277, 359 und 541 die ebenfalls in das Quadrat geschrieben werden. Das linke Quadrat zeigt das Zwischenergebnis.
Anschließend setzt Mag in die leeren Zellen, ohne erkennbarer Ordnung, weitere Zahlen ein, bis das Quadrat ausgefüllt ist. Das rechte Quadrat ist fertig.
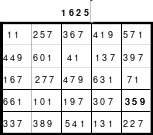
Mag erklärt abschließend, dass es ihm gelungen ist, trotz der Vorgaben, die er ja nicht einfach negieren kann, die richtigen Primzahlen gefunden zu haben und diese auch an die richtigen Stellen platziert hat.
(Mag will so suggerieren, dass es ohne die Vorgaben leichter gewesen wäre.)
Das so entstandene Quadrat ist magisch mit der magischen Summe 1625 entsprechend der Vorgabe. Alle Zahlen sind Primzahlen und keine kommt doppelt vor. Die Jury kann nach Prüfung diese Aussagen bestätigen.
Die Lösung
Die Primzahlen die eingesetzte werden sind natürlich keine beliebigen, sondern wie beim Topquadrat Zahlenreihen.
Mag ermittelte dazu Primzahlenreihen mit mindestens 5 Zahlen und mit einer Differenz von 30. Diese enden mit den Ziffern 1, 3, 7 oder 9. Mag reduzierte die Zahlen auf 3-stellige, wodurch nur Primzahlenreihen mit der Endziffer 1 und 7 zu finden waren. Lediglich 1 Reihe mit der Endziffer 9 konnten ermittelt werden und leider keine mit der Endziffer 3. Mag wollte aber die Zahlen nicht auf 4-stellige erhöhen und nahm dafür weniger attraktive Varianten in Kauf, wobei die Primzahlen mehrfach eingesetzt werden mussten, jedoch nie eine gleiche Kombination. Keine der magischen Summen ist doppelt. Mag hat 30 Kombinationen zusammengestellt. Sie sind, wie auch die Primzahlenreihen, nachfolgend aufgeführt.
Die Primzahlenreihen
Zahlenreihen mit der Endziffer 1 konnten nur 4 ermittelt werden. Mit der Endziffer 7 sind es 5 und nur eine mit der Endziffer 9. Jeweils 5 diese Primzahlenreihen sind die 5 Blöcke, die in das Pentaquadrat eingetragen werden.
5 der jeweils ersten Ziffern der Primzahlenreihen, verstärkt hervorgehoben, werden für die Karten, ca. Spielkartengröße, eingesetzt. Da Mag trotzdem wenigstens 30 Karten als erforderlich ansah, mussten die einzelnen Zahlen mehrfach verwendet werden. Mag war dabei bemüht, die Zahlen so zu kombinieren, dass keine doppelten magische Summen entstanden ist.
Die Zahlenkarten
Nachfolgen die 30 Primzahlenkarten, nach Größe der magischen Summen geordnet.
Die 5 mit kleinerer Schrift dargestellten Zahlen sind die jeweils ersten Zahlen der 5 Zahlenblöcke im 5er Pentaquadrat.
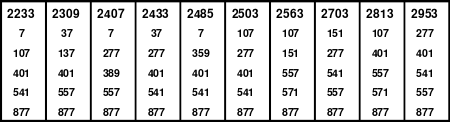
Halb gesprungen
Halb gesprungen bedeutet nicht, dass die Sprünge nur halb durchgeführt werden, sondern zuerst nur 2 Sprünge je Block und anschließend die restlichen 2 Sprünge. Damit soll die Regelmäßigkeit der Einordnung der Zahlen etwas verschleiert werden.
Links, das Pentaquadrat, entsteht durch springen innerhalb der Blöcke mit 2 nach rechts und 1 nach unten. Der Übergang zum nächsten Block ist 2 nach unten.
Die jeweils ersten Zellen des folgenden Blockes sind durch springen 2 nach links und 1 nach unten zu finden. Siehe dazu die fett gedruckten Zahlen. Diese Regel nutzt Mag für die Eintragung der vom Gast genannten Zahlen, nachdem die magische Summe als erste Zahl über das Quadrat geschrieben wurde.
Der Gast hat die Karte mit der magischen Summe 1625 und den Primzahlen 11, 137, 277, 359 und 541 gewählt.
Die Eintragung der 5 vorgegebenen Primzahlen ist im Quadrat 1 zu sehen.
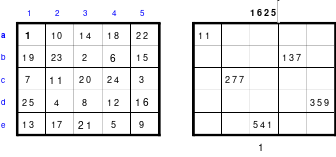
Nun kann das Springen beginnen. Von der 11 in Zelle 1a geht es zur Zelle 3b, in die 11 + 30 = 41 eingesetzt wird. Dann der 2. Sprung zur Zelle 5c in die 41 + 30 = 71 kommt. Es ist festzustellen, dass der 2. Sprung diagonal rechts/unten zur nächsten Vorgabe endet. Das trifft auch für alle weiteren Eintragungen zu, was aus dem Pentaquadrat auch erkennbar ist. Die nächste Vorgabe befindet sich folglich
diagonal nach links/oben. Von dort werden die nächsten 2 Sprünge vorgenommen. So wird weiter verfahren bis alle 2 ersten Sprünge erfolgt sind.
Das Quadrat 2 zeigt den Zwischenstand. Die hervorgehobenen Vorgaben dienen nur dem besseren Verständnis und sollten keinesfalls bei einer Vorführung verstärkt dargestellt werden.
Nun kann das Finale eingeläutet werden, die nächsten 2 Sprünge. Von der Vorgabe 11 nach recht/unten ist die 601, die Zahl des 2. Sprunges eines Blockes. Es ist völlig egal von welchem Block. Von dort aus werden die beiden weiteren Sprünge zu den Zellen 4c und 1d gemacht, in die die Zahlen 631 und 661 kommen.
Übrigens sind die Zahlenpaare aus Vorgabe und 2. Sprung des ersten Springens die einzigen die diagonal rechts/unten zueinanderstehen und somit leicht zu finden sind. Die nächste Zahl aus den 2 Sprüngen eines Blockes ist die 71 von der nach den
Zellen 2d und 4f gesprungen wird und die Zahlen 101 und 131 eingegeben werden. Die nächsten Sprünge gehen von der Zahl 197 aus zu den Zellen 5e und 2a in die die Zahlen 227 und 247 einzusetzen sind. Die nächsten Zahlen sind etwas schwieriger zu finden. Aber sie wissen ja Bescheid, wenn man unten ankommt, geht es einfach oben weiter und wenn man seitlich auf den Quadratrahmen stößt, geht es eben auf der anderen Seite einfach weiter. So ist das Finden der beiden restlichen Startzahlen 337 und 419 kein Problem. Sind die Sprünge der beiden letzten Startzahlen erfolgt, ist das Primzahlenquadrat mit der magischen Summe 1625 fertig und Sie können ihre Sprüche wie weiter vorn von sich geben, oder auch andere.
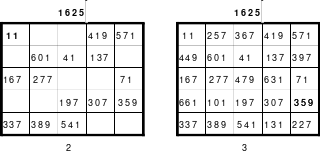
Das fertige Quadrat ist das Quadrat Nr. 3.
Eine Nachbetrachtung
Mag hat die einfache Variante vorgestellt. Es geht aber für den Zuschauer noch verwirrender, ist aber für Sie auch etwas schwieriger vorzuführen.
Bei der Eintragung der Vorgaben sind Sie nicht an eine Reihenfolge gebunden. Wichtig ist nur, dass die Abstände zueinander (2 links, 1 nach unten) eingehalten werden. Folglich ist der Gast nicht an eine Reihenfolge der Zahlenansage gebunden, er darf nur nicht eine Zahl 2-mal nennen. Aber das würden Sie ja gegebenenfalls selbst erkennen.
Weiter ist das Pentaquadrat ein pandiagonales und die Zelle 1a, in die in der Regel die erste Vorgabe eingesetzt wird, kann praktisch in jede andere Zelle durch Verschieben von Zeilen oder/und Spalten eingeordnet werden.
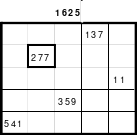
Deshalb ist es möglich, den Helfer zu bitten, die Zelle zu bestimmen, in die die erste Vorgabe eingesetzt werden soll.
Das linke Quadrat zeigt ein mögliches Beispiel einer Starsituation, die entsteht, wenn der Gast die zweite Zelle in der 2 Zeile bestimmt und als erste Zahl 277 nennt.
In diesem Fall ist es zur besseren Orientierung ratsam, die gewählte Zelle durch eine zusätzliche Umrandung zu kennzeichnen. Hat der Gast die Zelle genannt, zeigen Sie mit Ihrer Kreide auf die Zelle und fragen: “Diese hier?”. Nach der Bestätigung verstärken Sie den Rahmen dieser Zelle.
(Natürlich nur um diese unveränderlich festzuschreiben.)
Die nächste Zelle für eine Vorgabe ist auch mit 1 nach rechts und 2 nach unten zu finden, aber auch mit weiteren Springervarianten. Egal für welche Sie sich entscheiden, es sollte nur eine Variante genutzt werden.
Um die angewendeten Regeln nicht zu offensichtlich zu machen, hatte Mag die 4 Sprünge jedes Blockes in 2 mal 2 Sprünge aufgeteilt. Es ist aber auch möglich alle Sprünge einzeln durchzuführen. Dazu sind nur ein paar Regeln zu beachten. Der 1. Sprung von einer Vorgabe aus, endet immer in der Zelle links einer Vorgabe. Der 2. Sprung über einer Vorgabe, der 3. Sprung unter einer Vorgabe und der 4. Sprung in der Zelle rechts einer Vorgabe. Sie enden aber auch in den 4 diagonal zur Vorgabe befindlichen Zellen. Das rechte Quadrat zeigt das deutlich. Sie müssen sich für eine der Varianten entscheiden. Beherrschen Sie diese, können Sie ziemlich wahllos die Sprünge vornehmen. Die zweiten Sprünge gehen von jeder beliebigen Endzelle des ersten Sprunges aus, in der auch die zu erhöhende Zahl zu finden ist. Haben Sie mal einen Sprung übersehen und die Zelle z.B. für den Start des 2. Sprunges ist leer, so gehen Sie von der leeren Zelle zurück (mit 1 nach oben und 2 nach links) und finden so die Vorgabezahl von der aus Sie dann den Sprung nachholen.
Mag kann nicht alle Möglichkeiten aufführen, die sich aus diesem System ergeben. Es ist Ihre Entscheidung wie weit Sie Ihre Vorführungen qualifizieren wollen. Für alle Fälle gilt, Sie dürfen nur so weit gehen wie Sie es auch 100-prozentig beherrschen.
Variante 2 - “Nacheinander” **
Mag war mit der Lösung “Halb gesprungen” nicht ganz zufrieden, versuchte er doch stets auch eine Lösung zu finden, bei der die Zahlen Zeilenweise von links nach rechts eingetragen werden. Er hat eine solche gefunden.
Bei dieser Variante kommen die gleichen Primzahlenreihen und Karten wie in Variante 1 beschrieben zur Anwendung.
Wie bei “Halb gesprungen” entnimmt der Gast eine Karte mit 5 Primzahlen und der magischen Summe. Er nennt nach der Summe als 1. Zahl die 37. Mag schreibt diese in die erste Zelle der ersten Zeile. Werden die anderen 4 Zahlen genannt, schreibt Mag diese nicht in das Quadrat, sondern eine andere in die Zellen der ersten Zeile. Die Situation ist im linken Quadrat dargestellt. Nur die erste Zahl hat Mag übernommen. Die anderen 4 Zahlen 137, 151, 277 und 401 hat Mag durch die Zahlen 257, 241, 337 und 431 ersetzt. Eine solche Handlung wirft natürlich Fragen auf. Werden diese laut geäußert, erklärt Mag, dass er dazu zum Schluss eine Erklärung abgeben wird.
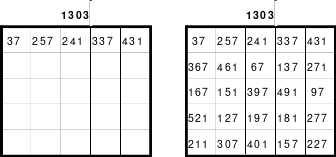
Mag schreibt anschließend zuerst Zahlen in die 2. Zeile, dann in die 3, weiter in die 4. und zum Schluss in die letzte, die 5 Zeile, und dass immer von links nach rechts.
Das fertige Quadrat ist rechts abgebildet. Es ist magisch, alle Zahlen sind Primzahlen, wovon keine doppelt vorkommt.
Auch hier kann Mag seine Erklärungen wie bei “Halb gesprungen” abgeben.
Weiter muss er natürlich die Frage nach den Zahlen in der 1. Zeile beantworten, auch wenn bei der Vorführung keine Frage nach dem Warum gestellt wurde.
Dazu erklärt er:
“Die genannten Zahlen konnte ich nicht in die obere Zeile einfügen, weil sie zusammen nicht die magische Summe von 1303 ergeben. Sie können das nachrechnen. Deshalb war ich gezwungen solche Primzahlen einzusetzen die die magische Summe von 1303 ergeben. Die genannten Zahlen musste ich an anderer Stelle einsetzen. was nicht ohne Schwierigkeiten bewältigt werden musste.”
Er zeigt auch, wo er diese eingesetzt hat.
Die Lösung
Die Lösung ist eigentlich ganz einfach und kann aus dem Pentaquadrat (1) abgeleitet werden.
Die Umsetzung der Regeln, um zum Ergebnis zu kommen, erfordert jedoch eine gewisse Konzentration. Diese ist aber beherrschbar. Die Regeln die zum Erfolg führen sind einfach zu verstehen und sicherlich Ihnen bekannt. Trotzdem geht Mag auf diese ein. Die Regeln sind:
Alle Zahlen eines Blockes werden im Springersystem, 2 nach rechts, 1 nach unten (vorwärts), eingesetzt. Springt man von der letzten Zahl eines Blockes weiter, kommt man auf die 1. Zahl des Blockes. Siehe dazu in (1) Sprung von 10 nach 6. Umgekehrt muss gesprungen werden, wenn man die letzte Zahl sucht, die um 1 erhöht werden soll. Also 2 nach links und 1 nach oben (rückwärts).
Das Pentaquadrat ist homogen, das heißt, in jeder Zeile befinden sich aus jedem Block eine Zahl und jeweils eine 1., 2., 3., 4. und 5. Zahl eines Blockes. Das trifft auch auf die 1. Zeile zu. Die 1 ist die erste Zahl des 1. Blockes, die 10 ist die 5 Zahl des 2. Blockes, die 14 ist die 4. Zahl des 3. Blockes, die 18 ist die 3. Zahl des 4. Blockes und die 22 ist die 2. Zahl im 4. Block.
Prüft man, wo sich die 1. Zahl des jeweiligen Blockes befindet, erkennt man als Regel, dass die Nummer der Zeile die gleiche Nummer der Spalte ist, in der sich die Ausgangszahl befindet. (Siehe dazu Quadrat 1.)
Beispiele: 10 in Spalte 2, 6 in Zeile 2 (blau); 14 in Spalte 3, 11 in Zeile 3 (grün);
18 in Spalte 4, 16 in Zeile 4 (rot); 22 in Spalte 5, 21 in Spalte 5 (gelb)
Weiter muss noch geklärt werden, in welcher Spalte sich die jeweils ersten Zahlen befinden. Das lässt sich leicht unter Beachtung der erfolgten Sprünge berechnen.
Um von der Zelle 2a (10) zur Zelle 4b (6) zu gelangen ist 1 Sprung erforderlich. Das heißt 2 Zellen nach rechts. Von der Zelle 3a (14) zur Zelle 2c (11) sind 2 Sprünge erforderlich, also 2 * 2 = 4 nach rechts, oder 1 nach links (5 - 4 = 1). Eine Zeile tiefer, in der 4. Zeile, ist die 1. Zahl für die 18 in der Zelle 4a zu finden. Das sind 3 Zeilen tiefer, wozu 3 Sprünge notwendig sind. 3 * 2 = 6, oder 6 - 5 = 1, rechts und dort ist die Zelle 5a. Genau so wird auch die Zelle mit der 21 für die Ausgangszahl 22 in Zelle 5a gefunden. 5. Zeile bedeutet 4 Sprünge. 4 * 2 = 8 - 5 = 3. Die richtige Zelle befindet 3 Zellen nach rechts, oder 2 Zellen nach links, ausgehend von der Spalte 5, wo sich die 22 befindet und man gelangt zur Zelle 3e für die erste Zahl im Block, die 21.
Wer nicht rechnen will, muss sich merken: 2 rechts, 1 links, 1 rechts, 2 links, was in der Abbildung 1 ersichtlich ist.
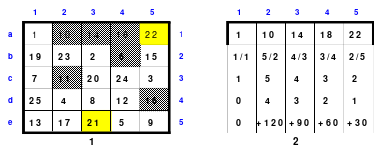
Die weiteren Betrachtungen beziehen sich auf die Abbildung 2. In der oberen Zeile befindet sich die 1. Zeile des Pentaquadrates. Darunter ist angegeben, die wievielte Zahl diese in welchem Block ist. Da die Blöcke nicht beachtet werden müssen, befinden sich in der 3 Zeile nur noch die wievielte Zahl im Block. In der nächsten Zeile ist dargestellt, um wie viel die Zahlen in der 1. Reihe gegenüber der 1. Zahl im Block erhöht ist. Diese Zahlenfolge 4 3 2 1 muss man sich immer vor Augen halten. Da die Differenzen zwischen den Primzahlen 30 sind, muss folglich die Erhöhung das 30-fache sein. Das bedeutet, die 2. Zahl in der 1. Reihe muss um 4 * 30 = 120 erhöht werden, die 3. um 3 * 30 = 90, die 4. um 2 * 30 = 60 und die 5. um 1 * 30.
Damit schließt Mag die theoretische Seite ab und kommt zur praktischen.
Der Gast hat die Karte mit der magischen Summe 1303 und den Primzahlen 37; 137; 151; 277 und 401 gewählt.
Der Gast nennt als erstes die “große Zahl”, die Mag als magische Summe über das Quadrat schreibt. Die nächste Zahl 37 schreibt Mag in die 1. Zelle der 1. Zeile. Nennt der Gast die nächste Zahl 137, so addiert Mag 4 * 30 = 120 dazu und erhält 257, die er in die nächste Zelle schreibt. In die nächste Zelle kommt 151 + 3 * 30 = 241. Die folgende Zahl 277 wird um 60 (2 + 30) auf 337 erhöht und die letzte Zahl 401 um 30 auf 431. (Jetzt wissen Sie, warum Sie sich die Zahlenfolge 4-3-2-1 merken sollten!) Das Zwischenergebnis ist im linken Quadrat ersichtlich.
Nun werden Zahlen von links nach rechts in die 2. Zeile eingetragen.
Dazu wird als erstes geklärt, wo sich die 1. Zahl des Blockes zur obersten Zahl der 2. Spalte befindet. Ein Sprung, 2 nach rechts und 1 nach unten, die 4. Zahl in der Reihe. Die erste Zahl in der 2. Reihe wird folgendermaßen berechnet. Von der Zelle wird rückwärts gesprungen, das ist 2 nach links und 1 nach oben, oder 3 nach rechts und 1 nach oben zur 337. Diese wird um 30 auf 367 erhöht und eingesetzt. In gleicher Weise wird die 2. Zahl in der Zeile gebildet, als 2 nach links oder 3 nach rechts und 1 höher zur 431 die um 30 auf 461 erhöht wird. (in der weiteren Folge spart sich Mag die Bemerkung “1 höher”, denn sie ist für alle Zeilen gültig.) Die 3. Zahl ist dann 37 + 30 = 67. In die 4. Zelle kommt die 1. Zahl des Blockes von der 2. Zahl in der 1. Zeile, die 257, von der die anfangs zugeschlagenen 120 wieder abgezogen werden und man erhält 137. Die letzte Zahl ist dann 241 + 30 = 271.
Wie in der 2. Zeile wird auch in den weiteren Zeilen verfahren. Zuerst wird die Zelle für die 1. Zahl des Blockes zur zugehörigen Zahl in der 1. Zeile ermittelt. Anschließend werden die Zahlen durch einen Rückwärtssprung zur vorhergehenden Zeile berechnet.
Der Rückwärtssprung zur darüber liegenden Zeile erfolgt immer 2 nach links oder 3 nach rechts. So braucht man die Begrenzung des Quadrates nicht zu überschreiten.
Die Zahlen für die 3. Zeile werden jetzt in Kurzfassung ermittelt.
Die 1. Zahl des Blockes für die 3. Zahl in der 1. Reihe befindet sich 2 * 2 = 4 Zellen weiter rechts, oder 2 Zellen nach links, das ist die 2. Zelle in der Zeile. In die 1. Zelle kommt - Rückwärtssprung zur 137 + 30 = 167. In die 2 Zelle 241 abzüglich der anfangs zugeschlagenen 90 = 151. Dann weiter mit 367 + 30 = 397, 461 + 30 = 491 und 67 + 30 = 97.
Zur 4. Zeile: Die 1. Zahl des Blockes für die 4. Zahl in der 1. Zeile 337 befindet sich 3 * 2 = 6 - 5 = 1 nach rechts, das ist die letzte Zelle in der 4. Zeile, in die später 337 - 60 = 277 eingesetzt wird. In die 1. Zelle kommt 491 + 30 = 521 und weiter 97 + 3 = 127, 167 + 30 = 197, 151 + 30 = 181 und in die letzte die bereits genannte Zahl 277.
Auch für die 5. Zeile gilt, dass zuerst die Zelle für die 5. Zahl in der 1, Zeile gefunden wird. Diese ist 4 * 2 = 8 - 5 = 3 rechts bzw. 2 links. Dort kommt später die Zahl 431 - 30 = 401 rein. In die 1. Zelle kommt 181 + 30 = 221 und weiter 277 + 30 = 307, dann die 401 und weiter 121 + 30 = 151 und die letzte Zahl 197 + 30 = 227.
Geschafft! Das Primzahlenquadrat ist fertig. Die Summen aller Reihen haben die magische Summe von 1303. Alle Zahlen sind Primzahlen und sind nur einmal vorhanden. Die Jury wird das nach Prüfung bestätigen.
Es bleibt noch die Erklärung, wo die vom Gast genannten 4 Zahlen geblieben sind. Die erste (37) ist ja in der 1. Zelle der 1. Zeile vorhanden.
Schauen Sie doch mal zu “Halb gesprungen”, dort werden ja die Zahlen des Gastes als erste in das Quadrat eingetragen. Das ist von der 1. Primzahl aus, im Beispiel 37, 3 nach rechts und 1 nach unten, oder 2 nach links und 1 nach unten. Dort finden Sie die Zahlen 37, 137, 151, 277 und 401.
Auch wenn die Erläuterungen vielleicht etwas schwierig erscheinen sollten, das Ganze ist nicht schwierig, sondern sehr einfach. Das erkennen Sie spätestens, wenn Sie die einzelnen Schritte zur Zahlenfindung anhand des rechten Quadrates verfolgen.
Trotzdem, es geht auch noch einfacher. Sehen Sie dazu in die Nachbetrachtungen von Mag.
Eine Nachbetrachtung
Eine Analyse zeigte, dass rd. 50 % der magischen Summen ebenfalls Prinzahlen sind. Das veranlasste Mag, nach weiteren Möglichkeiten zu suchen, mit dem Ergebnis, dass er 39 Zahlenkombinationen gefunden hat, deren magische Summen Primzahlen sind. Mag hat dies jedoch nicht zum Anlass genommen die Beschreibung zu “Halb gesprungen” zu überarbeiten.
Nachfolgend sind die 39 Primzahlenreihen abgebildet.
Dabei hat Mag Abstand genommen, die Zahlen zu sortieren. Er ist der Meinung, dass so eher eine Vielfältigkeit gesehen wird und auch die Primzahlen nicht nach einem Prinzip aufgebaut wirken. Trotzdem können die Zahlenreihen nicht befriedigen. Deshalb empfiehlt Mag die Anzahl der Karten auf 20 zu reduzieren, oder die Primzahlen zu erweitern. Doch auch hier sind Grenzen gesetzt, konnten doch nur 10 weitere Primzahlenreihen mit 5 Gliedern und gleicher Differenz aus Zahlen bis 10.000 gefunden werden.
Eine Erweiterung mit diesen Primzahlenreihen ist nicht ratsam, wenn die folgenden Ausführungen zur Anwendung kommen sollen.
Zu den Zahlenkarten:
Mag schlägt vor, auch die Primzahlen der magischen Summe zwischen den 5 übrigen Primzahlen unterschiedlich einzuordnen. Die Zahlen der magischen Summe sind Tausenderzahlen und damit leicht zu erkennen. Mag bittet den Gast die Zahlen in beliebiger Reihenfolge zu nennen, jedoch keine zweimal. 2- oder 3-stellige Zahlen werden nacheinander in die 1 Zeile eingeschrieben. Dabei werden die 2. bis 5. Zahl um die Beträge 120 bis 30 erhöht. Nennt der Gast die Tausenderzahl so schreibt Mag diese als magische Summe über das Quadrat.
Das Finden der Zelle für die 1 Zahl des Blockes:
Man muss dazu nicht von der entsprechenden Zahl in der 1. Zeile die erforderlichen Sprünge machen, sondern findet diese wie nun schon mehrfach erläutert. Das ist, ausgehend von der 1. Zahl in der 1. Zeile 3 nach rechts und 1 nach unten, bzw. 2 nach links und 1 nach unten zur 1. Zahl des Blockes, zu der die 2. Zahl in der 1. Zeile gehört. So geht es weiter - 3 nach rechts und 1 nach unten, jetzt besser 2 nach links 1 runter zur 1. Zahl des Blockes zu dem die 3. Zahl in der 1. Reihe gehört. Mit den gleichen Sprüngen erreicht man die Zellen für die weiteren 1. Zahlen. Diese Sprünge weichen von den üblichen Sprüngen 2 rechts, 1 nach unten ab. Um Missverständnisse auszuschließen nennt Mag diese Sprünge “Sondersprung”.
Die richtige 1. Zahl des Blockes ermittelt:
Vergessen Sie die Suche nach der zugehörigen Zahl in der 1. Zeile, von der Sie die anfangs unterschiedlichen zugeschlagenen Werte von 120 bis runter auf 30 abziehen müssen. Das können Sie einfacher haben. Wenn die Zelle für die 1. Zahl gefunden ist, geht man einfach einen Sprung rückwärts und zieht von der dort befindlichen Zahl 120 ab und man hat die 1. Zahl des Blockes.
Zum Beispiel:
Nach 2 Sondersprüngen von der Zelle 1a aus, kommt man auf die 2. Zelle in der 3. Zeile, Geht man nun einen normalen Sprung zurück, gelangt man zur 5. Zelle in der 2. Zeile. Dort befindet sich bereits die Zahl 271. Von dieser 120 abgezogen ergibt 151, die richtige Zahl.
Ebenso erhält man für die mittlere Zelle in der 5. Zeile 521 - 120 = 401.
Das ist ganz logisch. Denn nach einer letzten Zahl im Block kommt man mit einem, Sprung weiter, zur 1. Zahl des Blockes. Die letzte Zahl eines Blockes ist bekanntlich um 4, in unserem Fall 4 * 30 = 120, größer als die erste Zahl im Block.
Die erste Zahl:
Das eingesetzte Pentaquadrat ist ein pandiagonales. Das bedeutet, dass durch Versetzen von Zeilen und/oder Spalten das Quadrat immer ein magisches bleibt. Daraus kann abgeleitet werden, dass die 1. vom Gast genannte Primzahl in eine vom Gast oder anderem Zuschauer gewählte Zelle eingesetzt werden kann. Der Rechenkünstler kann um die Angabe der Zelle bitten, in die die erste genannte Primzahl eingetragen werden soll. Die weiteren Zahlen müssen dann in die gleiche Zeile eingeordnet werden. (Warum nicht auch diese in frei gewählte Zellen, fragt sich mancher Zuschauer.)
Mag rät jedoch davon ab. Es führt zu einer zusätzlichen Belastung die sich negativ auf das Tempo der Vorführung auswirkt. Auch die Möglichkeit eines Fehlers ist wahrscheinlicher. Mag ist der Meinung, dass der zusätzliche Effekt nicht in einem guten Verhältnis zum Aufwand steht.
Zum Schluss:
Zum Schluss der Beschreibungen kann festgestellt werden, dass die von Mag erarbeitete Lösung der 2. Variante der Vorzug zu geben ist. Sie ist eleganter und einfacher in der Ausführung. Es kann mit Sicherheit angenommen werden, dass die Zuschauer keinerlei Regeln erkennen können, nach denen die Bildung des Quadrates erfolgt.
Nachteilig ist die Vorgabe der magischen Summe und weiteren 5 Primzahlen, was aber auch geschickt als zusätzliche Erschwernis verkauft werden kann.
Dafür dürfte andererseits die Bildung eines Quadrates mit Primzahlen eine Ausnahme in der Rechenkunst mit magischen Quadraten sein.
Variante 3 - “Varianten-Kombi” * *
Bei der 1. Variante störte Mag die Springerei, bei der man sich schnell mal verheddern kann und bei der 2., die Suche nach der Zelle für die ersten Zahlen der Blöcke. Um eine noch einfachere Lösung zu finden, hat Mag die Vorteile der beiden Varianten kombiniert und die Probleme einfach ausgeblendet.
Auf die Idee ist Mag aber erst nach Fertigstellung der Varianten 1 und 2 gekommen. Mag hatte vor, nur die 3. Variante als die einfachste in seinen Ausführungen zu belassen. Davon hat er Abstand genommen. Er hätte sonst die ganzen Darlegungen neu überarbeiten müssen. Auch betrachtet Mag die Variante 2 als die qualitativ bessere.
Da Mag sich entschieden hat, die Varianten 1 und 2 zu belassen, geht er in der Variante 3 nur noch auf das Wesentliche ein. Es ist deshalb notwendig, sich vorher mit diesen beiden Varianten vertraut zu machen.
Ablauf der 3. Variante
Zum Einsatz kommen nur noch 21 Karten mit je 6 Primzahlen. Davon ist nur eine Tausenderzahl, die magische Summe. Diese ist in die übrigen 5 Primzahlen unsortiert eingesetzt.
Der Gast hat die Karte mit den Zahlen 277, 137, 571, 1303, 7 und 11 gewählt. Er nennt die Zahlen in beliebiger Reihenfolge und Mag setzt diese auch in beliebiger Reihenfolge in das Quadrat. Egal in welcher Reihenfolge der Gast die Zahlen nennt, Mag setzt die 1. Zahl in die 1. Zelle der 1. Zeile. Die 2. Zahl in die 4. Zelle der 2. Zeile. Um ein System der Einordnung zu verschleiern, setzt Mag die nächste Zahl in die mittlere Zelle der untersten Zeile, weil er weiß, dass dort auch eine der Zahlen eingesetzt wird. Dann folgen die weiteren 2 Zahlen, die er in die 2. Zelle der 3. Zeile und in die 5. Zelle der 4. Zeile eingeschrieben werden. (Die Folge der Einordnung wurde bereits mehrfach beschrieben.) Diese Reihenfolge unterbricht Mag nur, wenn der Gast die Tausenderzahl nennt, die er als die Magische Summe über das Quadrat schreibt. Dieser Zwischenstand entspricht der Abbildung 1.
Nun werden in alle leeren Zellen, Zeile um Zeile und immer von links nach rechts Primzahlen in das Quadrat eingesetzt, bis es fertig ist.
Das fertige Quadrat ist in Abbildung 3 zu sehen. Es ist magisch und pandiagonal. Alle Zahlen sind Primzahlen und keine kommt 2-fach vor.
Mag war es gelungen, trotz der Vorgaben, die in das Quadrat eingeordnet werden mussten, ein magisches Quadrat mit der vorgegebenen magischen Summe von 1303 zu bilden.
Welche Zahlen der Reihe nach einzusetzen waren, dürfte bekannt sein, wenn die Varianten 2, wie auch die 1., ausgewertet wurde. Trotzdem geht Mag nochmals darauf ein.
In die 2. Zelle der 1. Zeile wird die bereits eingetragene Zahl in der 2. Reihe um 120 erhöht und eingesetzt. Das ist 7 + 120 = 127.
In die 3. Zelle der 1. Zeile wird die bereits eingetragene Zahl in der 3. Reihe um 90 erhöht und eingesetzt. Das ist 571 + 90 = 661.
In die 4. Zelle der 1. Zeile wird die bereits eingetragene Zahl in der 4. Reihe um 60 erhöht und eingesetzt. Das ist 11 + 60 = 71 und
in die 5. Zelle der 1. Zeile wird die bereits eingetragene Zahl in der 5. Reihe um 30 erhöht und eingesetzt. Das ist 137 + 30 = 167.
Alle anderen Zahlen werden wie bekannt eingesetzt. Dazu wird die Zahl, die sich in der darüber liegenden Zeile, 2 Zellen nach links, oder 3 Zellen nach rechts befindet, um 30 erhöht und eingesetzt.
Das wäre für die 2. Zeile von links nach rechts 71+30=101, 167+30=197, 277+30=307, die folgende Zelle enthält bereits die Zahl 7. Deshalb weiter mit Zelle 5 in der 2. Zeile mit 661+30=691.
So wird Zeile um Zeile fertig gestellt, bis hin zur 5. Zeile, in die die Zahlen 601+30=631, 11+30=41, die 137 überspringen und weiter mit 367+30=397 und 67+ 30 =97 und fertig!
Schlussbemerkungen
Sie werden zugeben müssen, dass die 3. Variante die leichteste ist und ohne Schwierigkeiten vorgeführt werden kann, aber bitte nur, wenn sie das in weniger als 4 Minuten schaffen.
Der Variante 2 ist jedoch der Vorzug zu geben. Bei dieser Variante wird es selbst dem sachkundigen Zuschauer schwer fallen ein System des Quadrataufbaus zu erkennen.
6.4.6. Vorgabe einer Primzahl * * (Ein Experiment der ”Hohen Schule”)
Dieses Experiment ist analog der Beschreibung unter “Primzahlenquadrate der 4. Ordnung - Vorgabe einer Primzahl”.
Mag hat lange gezögert, das Experiment auf das Quadrat der 5. Ordnung zu übertragen, denn die Anforderungen sind wesentlich höher als beim Topquadrat. Waren beim Topquadrat 3 Primzahlen und deren Summe zu merken, sind es beim Pentaquadrat 4 Primzahlen und die Summe dieser. Beim Topquadrat konnten die Primzahlenreihen mit einer Differenz von 30 genutzt werden, wobei die Liste aus der ein Zuschauer eine Primzahl wählen konnte 26 Primzahlen enthielt. Bei Einsatz der 30er Reihen konnten nur 14 Zahlenreihen mit 5 Primzahlen ermittelt werden. Für eine Liste verblieben nur 10 Primzahlen. Es musste deshalb auf die Primzahlenreihen mit einer Differenz von 210 ausgewichen werden. Hier konnten 21 Primzahlenreihen gefunden werden. Da der Akteur 4 für sich beansprucht, verbleiben für eine Liste lediglich 17 Primzahlen. Das ist nicht attraktiv genug. Mag schlägt deshalb vor, eine Primzahlenliste einzusetzen, die alle ersten 5 Primzahlen der 210er Reihen enthält. (Siehe rot umrandete Primzahlen)
Die Primzahlenreihen mit einer Differenz von 210:
5 dieser Reihen enthalten mehr als 5 Primzahlen. Durch Nutzung aller Möglichkeiten können 21 Reihen mit je 5 Primzahlen gebildet werden (fett gedruckte Zahlen als erste der Reihen). Die blau schattierten Reihen beansprucht Mag für sich, weshalb nur noch 17 Primzahlen für eine Liste (1) verbleiben.
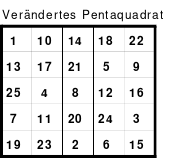
Die Berechnungen für das Quadrat erfolgen analog der Routine “Einfach Clever”. So kommt auch hier das in “Einfach Clever” eingesetzte veränderte Pentaquadrat zu Anwendung. Die Flexzahlen werden ersetzt durch die reservierten Primzahlen 23, 71, 157 und 353, die um das 1- bis 4-fache der Differenzzahl 210 erweitert werden. Die Erweiterung ist abhängig von der Einordnung in die oberste Zeile des Quadrates. Die Summe aller berechneten Einzelwerte ergibt den Festwert von 2704, der wie die Primärzahl eingesetzt wird. Siehe dazu nachfolgende linke Tabelle.
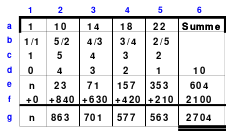
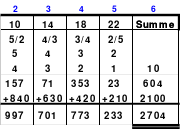
In der Zeile a sind die Zellenzahlen der obersten Reihe des veränderten Pentaquadrates zu finden. Die Zeile d gibt an, um wie viele mal die Schlüsselzahl / Faktor multipliziert werden muss. Sie entsprechen den Multizahlen bei “Einfach Clever”. Sie sind absteigend von 4 bis 1 eingeordnet und müssen gut gemerkt werden. Die Differenz zwischen den Primzahlen der Primzahlenreihen wird wie eine Schlüsselzahl bzw. Faktor behandelt. Er beträgt 210 und kann nicht verändert werden. In der Zeile e befinden sich die 4 Primzahlen, die bestens gemerkt werden müssen. Die einzige Veränderung die zulässig ist, ist die Einordnung der reservierten 4 Primzahlen in die Spalten 2 bis 5 der Zeile e. Die rechte Tabelle zeigt eine derartige Veränderung, die eine Veränderung der Einzelwerte, aber keine Veränderung aller anderen Zahlen und Werte zur Folge hat. Deshalb sollte auf derartige Veränderungen verzichtet werden. Sie bringen nur zusätzlichen Aufwand, der ohnehin schon ziemlich hoch ist.
Es müssen nämlich im Gedächtnis behalten werden:
Die 4 Primärzahlen 23, 71, 157 und 353
Der Festwert 2704 und die
absteigende Multizahlenreihe 4-3-2-1
Als weitere Erschwernisse sind zu nennen:
Die Berechnung der Einzelwerte, die den Flexzahlen in “Einfach Clever” entsprechen, wobei die Primzahlen um das 4- bis 1-fache von 210 erhöht werden.
Die Berechnung der magischen Summe durch Addition der Vorgabe zum Festwert 2704. und weitere.
All das ist für einen versierten Rechner kein Problem, dürfte aber für manchen Neuling vielleicht auf Ablehnung stoßen.
Wegen dieser Erschwernisse wurden dieser Routine 2 Sterne zuerkannt.
Bildung eines Quadrates
Ein Zuschauer wählt aus der ihm übergebenen Primzahlenliste (1) die Primzahl 467 aus. Ein weiterer Zuschauer nennt als Anfangszelle die 2. Zelle der 3. Zeile, in die Mag die Primzahl 467 einsetzt.
Anschließend schreibt er über das Quadrat die Zahl 3171, die magische Summe. Diese hat er mit 2704+467 = 3171 errechnet.
Hinter die Zuschauerzahl 467 schreibt Mag 863 (23+4*210) und weiter 701 (71+3*210), 577 (157+2*210) und in die 1. Zelle der gleichen Zeile 563 (353+1*210). Dieser Stand ist im linken Quadrat zu sehen.
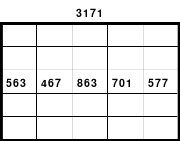
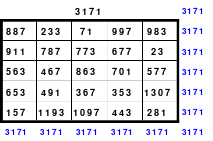
Weiter geht es mit der nächsten Zeile, links beginnend. Von dort 1 nach oben und 2 nach rechts. Dort steht die 863. 863-210=653, die in die 1. Zelle kommt. Zur nächsten Zelle und von dort wieder 1 nach oben und 2 nach rechts zur 701. 701-210=467, eintragen. So geht es weiter bis zur letzten Zelle in der Zeile. 1 nach oben 2 nach rechts. Dort steht die Vorgabe 467. Diese ist die 1. Zahl im Block, weshalb 210 nicht mehr abgezogen werden darf, sondern 4*210=840 zugerechnet werden muss. Das ist 1307.
Die unterste Zeile wird ebenso berechnet. In die 1. Zelle kommt 157 (367-210=157). Aber Achtung, von der 2. Zelle 1 nach oben und 2 nach rechts, dort steht 353. 353 ist eine der reservierten Primzahlen und gilt als 1. in ihrem Block. Deshalb muss diese um 4*210=840 auf 1193 erhöht werden.
Ein solcher Fall tritt in jeder Zeile einmal auf. Die Erkennung ist nicht wie bei “Einfach Clever” eine Null als letzte Ziffer, sondern eine der 4 Primzahlen die in die Einzelwerte eingehen.
Jetzt geht es mit der 1. Zeile weiter. Hier ist die unterste Zeile die Bezugszeile aus der die um 210 zu reduzierenden Zahlen und die um 840 zu erhöhende Zahl entnommen werden.
Das fertige Quadrat ist das rechte. Es ist magisch und pandiagonal. Alle Zahlen, außer der magischen Summe, sind Primzahlen, von denen jede nur einmal vorhanden ist. Die magische Summe ist 3171, wie es Mag vorher über das Quadrat geschrieben hat.
Das Ergebnis ist recht attraktiv, nicht aber die zu klein geratene Primzahlenliste.
Mag hat nach Möglichkeiten der Erweiterung der Liste gesucht und bietet 2 Alternativen an, die nachfolgend beschrieben werden.
Alternative Primzahlenlisten
Um größere Listen mit Primzahlen dem Zuschauer anzubieten, hat Mag die erweiterte (2) und die große (3) Primzahlenliste aufgestellt.
Die erweiterte Liste enthält zusätzlich 4-stellige Primzahlen. Diese sind die magischen Summen die durch Addition des Festwertes zu den Zahlen in Liste 1 entstanden sind. Leider konnten von diesen Summen nur 5 als Primzahlen ermittelt werden. Die List 2 ist deshalb nur unwesentlich größer als Liste 1.
Beim Einsatz der Liste 2 kann es zur Vorgabe einer 4-stelligen Primzahl kommen. In diesem Fall wird die Vorgabe als magische Summe über das Quadrat geschrieben. Durch Abzug des Festwertes von der Vorgabe erhält man die Zahl für die Zelle 1. Die Zahlen für die weiteren Zellen werden wie bekannt abgearbeitet.
Zum Schluss kann zusätzlich darauf hingewiesen werden, dass alle Zahlen, auch die magische Summe, Primzahlen sind.
Die Liste 3 enthält die anfangs gezeigten Primzahlenreihen, jedoch nur den rot eingerahmten Teil und ohne die von Mag beanspruchten Reihen. Die aus mehr als 5 Primzahlen bestehenden Reihen abgeleiteten weiteren Primzahlenreihen wurden nicht in die Liste aufgenommen, da diese zu doppelten Zahlen führen würden.
Die Gefahr, dass der Zuschauer erkennen kann, dass die Zahlen der einzelnen Reihen eine Differenz von 210 haben, ist nicht besonders groß. Und wenn es der Fall ist, kann er sicherlich mit der Erkenntnis nicht viel anfangen. Trotzdem sollte zur Sicherheit nur eine Liste an einen bereiten Zuschauer ausgegeben werden.
Die etwas attraktivere Liste hat aber eine zusätzliche Berechnung zur Folge.
Hat der Zuschauer seine Zahl gesagt, wird er gebeten die Spalte zu nennen, aus der er die Zahl entnommen hat. Leiter ist diese Frage nicht zu umgehen.
Nach der Wahl der Zelle mit der begonnen werden soll, trägt Mag die Vorgabe in diese ein.
Die leicht veränderten Berechnungen werden an einem Beispiel erläutert.
Zum besseren Verständnis nennt Mag die von ihm beanspruchten Primzahlen 23, 71, 157 und 353 Eigenzahlen.
Der Zuschauer nennt aus der Liste 3 die Primzahl 619 aus der 3. Spalte. Er, oder ein weiterer Zuschauer nennt für den Anfang die 3. Zelle in der 2. Zeile, in die Mag die Vorgabe 619 einsetzt. Da die 3. Spalte angegeben wurde, weiß Mag, dass die erste Primzahl der zugehörigen Reihe um 2*210=420 kleiner ist und das ist 619-420=199. Diese Primzahl sollte man sich möglichst merken. Die magische Summe errechnet Mag durch Addition der 199 zum Festwert 2704 und erhält 2903, die er über das Quadrat schreibt.
Wer Bedenken hat, die 199 im Gedächtnis zu behalten, sollte nach 2 Returnsprüngen, das ist 2*2 nach links und 2*1 nach unten, auch 1 nach rechts und 2 nach unten, heimlich ein Zeichen setzen. Denn dort wird nach 2-maligen Abzug von 210 die 1. Zahl der Primzahlenreihe stehen, von der nicht mehr 210 abgezogen werden darf, sondern um 840 zu erhöhen ist. Mag hat diese Zelle mit einem Punkt versehen.
Mag erinnert an die abfallenden Multizahlen 4, 3, 2, 1 und 0.
Die Multizahl 2 wird durch die Vorgabe gebunden. Deshalb setzt Mag in die Folgezelle eine Eigenzahl, hier 23+1*210=233 ein. Für die nächste Zelle gilt die Multizahl 0, weshalb er die unveränderte Eigenzahl 71 dort einschreibt. Rechts angekommen geht es links weiter. Nach der Multizahl 0 kommt die Multizahl 4. Deshalb ist die Zahl für diese Zelle die Eigenzahl 157+4*210=997. Die letzte Primzahl dieser 2. Zeile ist Eigenzahl 353+3*210=983.
Das linke Quadrat zeigt dieses Zwischenergebnis.
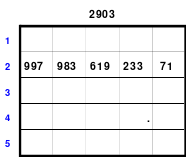
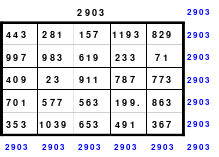
Weiter mit Zeile 3 nach dem bekannten Modus.
Von der 1. Zelle 1 nach oben und 2 nach rechts zur 619. 619-210=409, die in die 1. Zelle dieser Zeile eingetragen wird. In die nächste Zelle kommt 233-210=23. Von der 3. Zelle in Zeile 3 kommt man zur 71 und das ist eine Eigenzahl. Deshalb wird 71+840=911 in die 3. Zelle eingesetzt. So werden die Zahlen für alle anderen Zellen berechnet und eingesetzt. Von der 2. Zelle in Zeile 5 kommt man zur 199. Der Punkt verrät, dass es die 1. Zahl der Primzahlenreihe ist, aus der die Vorgabe stammt. Deshalb wird in die 2, Zelle der letzten Zeile 199+4*210=1039 eingesetzt.
Übrigens, den Punkt hätte Mag sich sparen können. Denn die Zahl 199 hatte er ja bei der Berechnung der magischen Summe ermittelt. Da von 199 keine 210 abgezogen werden kann, ist zu erkennen, dass es sich um eine 1. Zahl in den Primzahlenreihen handelt und als Erkennung genug ist. Der Punkt schadet nicht, außer er wäre notwendig und vergessen worden.
Das fertige Quadrat ist magisch mit der magischen Summe von 2903. Alle Zahlen sind Primzahlen und keine ist doppelt vorhanden.
Das die magische Summe auch eine Primzahl ist, ist reiner Zufall und auch nicht vom Akteur erkennbar.
Eine Nachbetrachtung
Durch die Anwendung des in “Einfach Clever” genutzten Systems, ist die Gestaltung eines Primzahlenquadrates bei Vorgabe einer Primzahl, eine realisierbare Möglichkeit, derartige Quadrate zu bilden.
Der Aufwand dazu steht positiv zum Ergebnis. Wann und wo wurden in öffentlichen Vorführungen derartige Experimente gezeigt? Mag sind keine bekannt.
Andererseits sollten die Nachteile nicht verschwiegen werden.
Als erstes muss auch hier die Frage nach den Möglichkeiten einer Vorführung genannt werden. Und wenn eine besteht, muss bedacht werden, dass manche Zuschauer nichts mit Primzahlen anfangen können und deshalb nicht gerade positiv zu derartigen Darbietungen stehen.
Die Liste 3 enthält Primzahlen die eine Differenz von 210 erkennen lassen. Auch wenn das als unbedenklich eingeschätzt werden kann, ein Schönheitsfehler bleibt es. Kleinere Listen sind aber als unzureichend abzulehnen.
Besonders negativ ist, dass eine Wiederholung des Experimentes nicht möglich ist. Wegen der feststehenden Eigenzahlen werden 80 % der Zahlen die der vorherigen Darbietung entsprechen. Ein Ausweg dazu wäre die Beherrschung weiterer Zahlenkombinationen, die eine einfache Berechnung sichern.
Nachfolgend einige Möglichkeiten.
Eigenzahlen 13, 23, 199 und 463 mit einem Festwert 2800-2
“ 23, 47, 199 und 396 “ “ “ 2500-4
“ 13, 23, 199 und 698 “ “ “ 2800-2
Mögliche Wiederholung von Zahlen sind mit diesen Eigenzahlen im geringen Umfang noch möglich, sind aber nicht mehr so auffällig und können in Kauf genommen werden.
Die Anwendung dieser Ausweichvarianten setzt allerdings auch voraus, dass diese 100%ig erlernt werden müssen, was eine zusätzliche Belastung ist. Des Weiteren erfordern sie veränderte Primzahlenlisten, die die jeweiligen Eigenzahlen nicht enthalten.
Weiter muss genannt werden, dass eine analoge Anwendung für das 7er Heptaquadrat ausgeschlossen ist, da die erforderlichen Primzahlenreihen dazu nicht zu finden sind.
Man kann über das Für und Wider diskutieren, Die gefundene Lösung ist beachtenswert, zumal es schwer ist, magische Quadrate aus Primzahlen zu bilden.
Wer sich zu einer Einordnung in sein Rechenprogramm berufen fühlt, kann es ja Übernehmen, allein die Wissenserweiterung zu den magischen Quadraten wird für den wahren Fan von Interesse sein und das ist ein Hauptanliegen von Mag, der mit diesen Worten den Abschnitt des Hexeneinmaleins mit Quadraten der 5. Ordnung abschließt.
6.4.7. Das rationelle 5er Quadrat
Mag ist der Meinung, dass die gezeigten Routinen im kleinen Hexen 1x1 eigentlich nicht mehr als klein bezeichnet werden können. Aufgrund der Größe des Pentaquadrates muss um größere Vorgaben als nur 2-stellige gebeten werden. Auch ist das Pentaquadrat wesentlich größer als das Lo-Shu- und Topquadrat, woraus sich auch ein größerer Zeitaufwand bei der Bildung eines solchen Quadrates ergibt. Um diesen zu minimieren, sind Möglichkeiten einer besseren Organisation des Ablaufes und einer einfacheren Berechnung der Zahlen zu nutzen. Dazu hat Mag in seinen Ausführungen bereits einiges aufgezeigt.
Mag wird nachfolgend weitere Beispiele zur Rationalisierung der Quadratbildung aufzeigen. Er setzt voraus, dass die vorangegangenen Ausführungen ausgewertet wurden. Das betrifft insbesondere die Berechnung eines Pentaquadrat bei Vorgabe einer Zahl oder der magischen Summe, sowie die Springer- und Dualmethode.
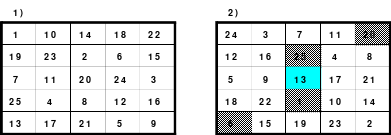
Das Quadrat 1 zeigt das Pentaquadrat. Durch Versetzen von Zeilen und Spalten befindet sich die Zelle 13, die mittlere Zahl der Zahlen von 1 bis 25 und mittlere Zahl des 3. Blockes in der Mitte. Unter der Zelle 13 ist die Zelle 1, die 1. Zahl des 1. Blockes zu finden. Über der Zelle 13 ist die Zelle 25, die letzte Zahl des 5. Blockes eingeordnet. Weiter von Bedeutung sind die Zellen 6 in der Ecke unten links und die Zelle 20 in der Ecke oben rechts. Die 6 ist die 1. Zahl des 2. Blockes und die 20 die 5. (letzte) des 4. Blockes. Die Zelle 20 wird durch einen Returnsprung von Zelle 25 ausgefunden und die Zelle 6 mit einem Linkssprung von Zelle 1 aus.
Die so gefundenen Zellen sind die Startzellen (SZ) von denen aus die restlichen Zahlen für die folgenden Zellen der Blöcke berechnet werden.
Diese Struktur der Startzellen ist im Quadrat 2 farblich hervorgehoben. Sie sind leicht zu merken, beziehungsweise durch die entsprechenden Sprünge schnell zu finden.
Nachstehen die anzuwendenden Sprünge
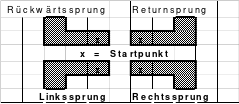
Die weiteren Erläuterungen gehen von einer Zahlenvorgabe von 742 aus. Sie ist eine 3-stellige Zahl aus dem oberen Bereich. Eine ähnliche Zahl könnte auch durch Vorgabe der magischen Summe, als 4-stellige Zahl aus dem unteren Bereich, entstehen.
Zum Quadrat 3
Die Vorgabe wird nach Nennung in die mittlere Zelle des Quadrates eingesetzt.
Die magische Summe wird wie bekannt durch Multiplikation der Zahlenvorgabe mit 5 errechnet. Rationell ist das auch: Vorgabe mal 10, indem eine Null angehängt wird, und anschließende Division durch 2.
Die berechnete magische Summe wird über das Quadrat geschrieben.
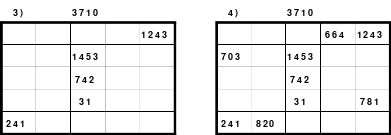
Das Startquadrat
Als erstes wird die Differenzzahl 1 (DZ1) gebildet. Diese ist eine Zahl kleiner als die Vorgabe 742 mit der ein leichtes Rechnen möglich ist. Im Beispiel wurde als DZ1 = 711 gewählt. Auch 689 (700-11) wäre eine Variante.
Mittels der DZ1 werden nun in einfacher Form die Zahlen für die Zellen 1 und 25 berechnet.
Die Zahl für Zelle 1 ist die Differenz zwischen der Vorgabe und der DZ1, das ist 742-711=31.
Die Zahl für die Zelle 25 ist das Doppelte der Vorgabe abzüglich der Zahl in Zelle 1, das ist 742*2=1484-31=1453 oder rationell gerechnet Vorgabe + DZ1 und das ist 742+711=1453 (richtig).
Nun könnten die Zahlen für die Zellen 2 bis 12 als aufsteigende und die Zahlen für die Zellen 24 bis 14 als absteigende Zahlenreihe eingetragen werden. Dazu muss die Schlüsselzahl mit DZ1/13, das ist 711/13 berechnet werden. Auch wenn diese Berechnung nicht schwierig ist, sie kostet Zeit. Nicht unbedingt vorteilhaft sind die stets gleichen Sprünge und gleichen Differenzen für die beiden Zahlenreihen, was bei größeren Quadraten auffälliger wird.
Günstiger ist es, vorher die Startzahlen für alle Blöcke zu berechnen. Die Berechnung ist einfacher und die Eintragungen der Zahlen können je Block getrennt erfolgen. Dabei muss keine Folge der Blöcke beachtet werden.
Die Berechnung der Startzahlen für die restlichen Blöcke, (beim 5er Quadrat nur noch 2, beim 7er Quadrat schon 4 und beim 9er Quadrat sogar 8), erfolgt mittels der Differenzzahl 2 (DZ2). Die Differenz zwischen den Zellen 1 und 13 entspricht rd. 2,5 Blöcke, oder Ordnungszahl/2 = OZ/2 = 5/2. 5/2 ist auch 10/4. Die Differenz zwischen den Zellen 1 und 13 ist die DZ1. Folglich wird die DZ2=DZ1*4/10= 711/10=71, rd. 70*4=280, gewählt 210. (211 wäre vielleicht günstiger gewesen!?)
Die Startzahl für die Zelle 6, der 1. im 2. Block, ist Zahl aus Zelle 1 plus DZ2. Das ist 31+210=241, die in die Zelle eingetragen wird, die mit einem Linkssprung von Zelle 1 ausgefunden wird.
Die Startzahl für die Zelle 20, der letzten im vorletzten, dem 4. Block ist, da absteigend, Zahl aus Zelle 25 minus DZ2 = 1453-210=1243. Die Zelle 20 wird mit einem Returnsprung von Zelle 25 aus erreicht.
Damit sind für alle 5 Blöcke die Startzahlen gefunden. Es sind im 3. Block die mittlere Zahl 13, im 1. und 2. Block die ersten Zahlen 1 und 6 sowie in den Blöcken 4 und 5 die letzten Zahlen 20 und 25.
Dieser erreichte Zwischenstand ist im Quadrat 3, dem Startquadrat, dargestellt.
Eine wichtige Erkenntnis ist, dass sich alle Startzahlen der aufsteigenden Zahlenreihen unterhalb der mittleren Zahl befinden und die der absteigenden oberhalb. Dabei befinden sich die jeweils letzten berechneten Startzahlen auf der 1. bzw. letzten Zeile. Man muss also die Anzahl der Startzahlen nicht abzählen, sie sind alle fertig ermittelt, wenn die Eintragung in der 1. bzw. letzten Zeile erfolgt ist.
(Das gilt für alle Quadratgrößen und erleichtert die Arbeit bei der Bildung größerer Quadrate!)
Um die restlichen Zellenzahlen zu berechnen ist noch die Schlüsselzahl (SZ) festzulegen. Geht man davon aus, dass jeder Block 5 Zahlen enthält, wobei 5 die Ordnungszahl ist, muss die Differenz zwischen den Blöcken (DZ2) durch die Ordnungszahl (O) dividiert werden. Die SZ wird im Beispiel 210/5= rd. 40, gewählt 39 (40-1) groß.
Im Quadrat 4 sind die Zahlen für den mittleren Block eingetragen. Von der mittleren Zahl 742 werden die aufsteigenden Zahlen durch Addition der Schlüsselzahl und nach einem Rechtssprung berechnet und eingetragen. Das sind die Zahlen 742+39=781 und 781+39=820. Auch trifft zu, dass sich die letzte aufsteigende Zahl des mittleren Blockes in der letzten Zeile befindet. Es muss nicht gezählt werden!
Analog werden die absteigenden Zahlen durch den jeweiligen Abzug der SZ und Rückwärtssprung ermittelt und eingeschrieben. Das sind die Zahlen 742-39=703 und 703-39=664. Auch hier befindet sich die zuletzt berechnete Zahl in der 1. Zeile.
Im Quadrat 5 wurden die aufsteigenden Blöcke bearbeitet. Von der Startzahl 31 in Zelle 1 ausgehend wurden die um jeweils der SZ erhöhten Zahlen nach Rechtssprüngen eingesetzt. Diese Zahlen sind 31+39=70+39=109+39=148+39=187. Springt man von Zelle 5 mit der Zahl 187 einen Rechtssprung weiter, gelangt man auf die Zelle 1 mit der Zahl 31. Das ist logisch, denn die Zahlen der Blöcke bilden in sich geschlossene Schlaufen. Damit entfällt auch hier das Zählen der Eintragungen. Der Block ist fertig, wenn es nicht mehr weiter geht.
In gleicher Weise wurden die Zahlen und Zellen für den 2. Block berechnet und ermittelt. Es sind die ausgehend von Zelle 6 mit der Startzahl 241 die Zahlen 280, 319, 358 und 397.
Die absteigenden Zahlen der Blöcke 5. und 4 wurden durch Abzug der SZ von den Startzahlen 1453 und 1243 aus beginnend berechnet und in Rückwärtssprüngen eingesetzt. Das sind ab der Startzahl 1453 in Zelle 25 die Zahlen 1453-39=1414 und weiter 1414-39=1375-39=1336-39=1297.
Auch hier kommt man mit einem weiteren Rückwärtssprung zur vorhandenen Startzahl 1453, womit der Block fertig berechnet ist. Mit der gleichen Abarbeitung werden die Zahlen des 4. Blockes ermittelt.
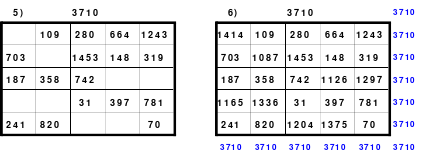
Das fertige Quadrat ist das Quadrat 6. Es ist magisch mit der als erstes berechneten magischen Summe von 3710 und pandiagonal.
Die Zahlen sind breit gestreut und zeigen keine Auffälligkeiten.
Hinweise
Einen Rest, der bei der Vorgabe der magischen Summe entstehen kann, wird zweckmäßig der berechneten Startzahl in der 1. Zeile zugeschlagen. Er wird dann der zuletzt berechneten Startzahl in Zeile 1 oder der untersten Zeile zugeschlagen. Er wird dann in jeder Zeile, Spalte und Diagonalen 1-mal wirksam.
Natürlich kann auch bei dieser Variante um die Nennung der Zelle gebeten werden, in die die erste Zahl eingesetzt werden soll. Voraussetzung ist, das Pentaquadrat wird gründlich beherrscht. Nachteilig ist dabei jedoch die Tatsache, dass dann die Eintragung der Startzahlen nicht in der 1. oder letzten Zeile enden. Deshalb sollte auf eine Vorgabe einer Anfangszelle verzichtet werden.
Nicht immer kann die DZ1 so günstig gebildet werden wie im Beispiel. Das trifft z. B. auf eine Zahl mit einer Null an letzter oder vorletzter Stelle zu. In solchen Fällen bietet sich eine DZ1 mit 09 als letzte Ziffern an. Sollten die letzten Ziffern der Vorgabe kleiner 09 sein, wird die Vorgabe um 100 reduziert und 99 für die letzten 2 Ziffern eingesetzt.
Mag hat der besseren Übersicht wegen erst die Auf- und dann die absteigenden Zahlenreihen bearbeitet. Besser ist eine abwechselnde Erstellung, weil dann ein Erkennen der Methode erschwert wird.
Mag hofft, dass er Sie von dieser rationellen Erstellung magischer Quadrate überzeugt hat. Sie gilt für alle Primquadrate und bei Triquadrate mit leichten Einschränkungen gleichermaßen.
Zwingend ist aber, dass die Quadrate als Springerquadrate mit einfachen Sprüngen, 2 rechts und 1 nach unten, gebildet werden. Die Übergänge von Block zu Block müssen einheitlich 2 nach unten sein.
6.5. Quadrat der 6. Ordnung
6.5.1. Der Sechser im Hexen 1x1 * *
Oft übt die Kritik, die von der Materie die geringsten Kenntnisse haben. Das musste auch Mag zur Kenntnis nehmen, als er wegen des fehlenden Quadrates der 6. Ordnung in der Rechenkunst des Hexen 1x1 kritisiert wurde. Und dass, obwohl er mehrfach begründet hat, dass das nahezu unmöglich ist. Trotzdem nahm Mag die Kritik zum Anlass, um nochmals nach einer brauchbaren Lösung zu suchen.
Er hat sie gefunden! Eine Lösung, die sicherlich auch Sie überrascht und ohne Schwierigkeiten realisierbar ist.
Ehe Mag die gefundene Lösung erklärt, möchte er beschreiben, wie es die Zuschauer erleben.
Die Vorführung
Der Vorführende bittet um eine Zahl kleiner 1000. Es wird 147 genannt, die er in die 1. Zelle der 2. Zeile schreibt. Nach einer kurzen Denkpause schreibt er über das Quadrat die Zahl 684. Anschließend, erst zögerlich, dann immer schneller, füllt er das Quadrat mit Zahlen aus. Keine Zahl ist doppelt und alle Zeilen, Spalten und die beiden Diagonalen haben die Summe von 684, die er anfangs über das Quadrat geschrieben hatte. Damit war dieses Quadrat der 6. Ordnung ein magisches. Es ist das unten abgebildete, das er in weniger als 5 Minuten erstellt hat.
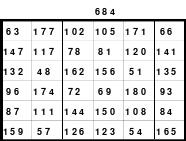
Die Idee
Mag ging davon aus, wenn man sich die Zahlenfolge im Hexaquadrat nicht oder nur sehr schwer merken kann, so muss ein 6er Quadrat gefunden werden, dass entsprechend einer leicht zu merkenden Struktur aufgebaut ist. Ein solches konnte Mag nicht finden. Er entschied sich deshalb, dass 6er Quadrat aus 4 Lo-Shu-Quadraten zusammenzufügen. Damit das Quadrat ein magisches wird, mussten alle 4 Lo-Shu-Quadrate gleiche magische Summen haben. Die Pendelmethode schied aus, da das Lo-Shu-Quadrat ein ungerades ist. Die Korrekturmethode kann nur angewendet werden, wenn eine ungerade Anzahl von Quadraten gebildet werden soll, was ebenfalls nicht zutrifft.
Die entscheidende Idee war, einfach 5 Korrekturquadrate zu bilden und davon nur 4 zu verwenden. Im 6er Ausgangsquadrat fehlen dann eben von den 45 Zahlen 9. Das ist aber bedeutungslos, weil die Zahlen im Hexen 1x1 ohnehin durch Multiplikation und/oder Addition verändert werden.
Diese Lösung erfordert aber, dass die Korrekturquadrate leicht gebildet werden können.
Auch dazu hat Mag eine einfache Lösung erarbeitet.
Die Anforderungen die sich aus dem gefundenen Lösungsweg ergeben sind je nach Vorgabengröße einfache Berechnungen die bewältigt werden können. Diese sind:
Man muss sich lediglich vier 3-stellige Zahlen, oder besser den logischen Aufbau der Matrix zur Bildung von Korrekturquadraten merken.
Des Weiteren eine 2-stellige Zahl mit 6 multiplizieren und zu einer 3- oder 4-stelligen, addieren können.
Alle weiteren Berechnungen sind bei kleinen Vorgaben einfach und werden deshalb erst in den weiteren Erläuterungen beschrieben.
Auch wenn das keine besonders hohen Leistungen sind, hat Mag dieser Routine 2 Sterne zuerkannt. Das erfolgt wegen den zusätzlichen sonstigen Anforderungen, insbesondere an ein logisches Denkvermögen und an das Gedächtnis, denn man muss sich einige Zahlen gut merken können.
Mag hat diese machbaren Bedingungen vorangestellt, weil die nachfolgenden Erläuterungen umfangreich und eventuell für manchen auch schwer verständlich sind. Das Ergebnis ist aber ein durchaus gangbarer Weg.
Und das Ergebnis ist das Entscheidende!
Der Lösungsweg
Wie bereits beschrieben entstehen die Korrekturquadrate durch den Austausch ganzer Blöcke zwischen den Wechselquadraten.
Die Wechselquadrate können sehr einfach gebildet und der Tausch der Blöcke aus einer einfach zu erstellenden Matrix entnommen werden.
Doch nun zu den Einzelheiten.
Die 5 Wechselquadrate
Nachfolgend sind 5 Wechselquadrate dargestellt.
Der Aufbau ist denkbar einfach. Begonnen wird im 1. Quadrat, bei dem in die Zelle 1 die Zahl 1 kommt. In die Zelle 1 des folgenden 2. Quadrates wird die 2 eingesetzt. So geht es weiter bis zum 5. Quadrat, wo in die Zelle 1 die 5 kommt.
Nun werden wieder von links nach rechts die folgenden Zahlen 6 bis 10 in die Zellen 2 eingesetzt. In gleicher Weise geht es weiter bis zur Zahl 45, die als letzte in die Zelle 9 des 5. Quadrates kommt.
Die Folge ist, dass in jedem Quadrat die Zahlen einen Abstand von 5 haben, was der Anzahl der Quadrate entspricht.
Es ist ein Leichtes, z. B. die Zahl in Zelle 7 des 4. Quadrates zu bestimmen:
In der Zelle 1 des 4. Quadrates befindet sich die 4.
7 ist im Originalquadrat um 6 größer als 1. Folglich ist die Zahl in Zelle 7 um 6*5 = 30 größer als die Zahl in Zelle 1. Das ist 4 + 30 = 34. Das trifft auf alle Quadrate zu. So ist die Zahl in Zelle 7 des 3. Quadrates 3 + 30 = 33.
Bei der Anwendung dieser Regeln werden nur die 1. Zahlen der Blöcke (1; 4 und 7) berechnet. Die Zahlen für die weiteren Zellen in den Blöcken werden einfach jeweils um 5 erhöht.
Die gebildeten 5 Quadrate sind zwar magisch, haben aber unterschiedliche magische Summen.
Um Quadrate mit gleichen magischen Summen zu erhalten, werden nach der Korrekturmethode Blöcke aus anderen Quadraten in das jeweilige Quadrat eingesetzt.
Dabei kommen nur Blöcke der gleichen Einordnung in Frage. Es wird zum Beispiel als 2. Block nur ein 2. Block eines anderen Quadrates zum Einsatz kommen.
Welcher Block aus welchem Quadrat in das jeweilige Quadrat eingesetzt werden muss, verrät eine einfach zu erstellende Matrix, die als Nächstes beschrieben wird.
Die Matrix
Nachstehend sind das Lo-Shu-Quadrat und die Matrix für die Bildung von 5 Korrekturquadraten abgebildet, wie sie bereits unter “Korrekturquadrate” beschrieben wurde.
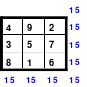
Dazu die Erklärung.
Die linken roten Zahlen stehen für die Quadrate 1 bis 5.
Die grünen Zahlen oben sagen um welchen Block es sich in den Quadraten handelt.
Die schwarzen Zahlen in dem grünen Feld geben Auskunft, aus welchem Quadrat der entsprechende Block eingesetzt werden muss.
Zum Beispiel: In das 3. Quadrat (rote Zahl 3) muss als 2. Block (grüne Zahl 2) der 2.
Block aus Quadrat 1 (schwarze Zahl 1) eingeordnet werden.
Von der Richtigkeit dieser Einordnungen können Sie sich anhand der folgenden Quadrate überzeugen.
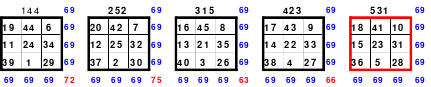
In der oberen Reihe befinden sich die 5 Wechselquadrate. In der unteren sind die entstandenen Korrekturquadrate abgebildet.
Über diesen sind die so genannten Kennzahlen zu sehen. Das sind die jeweils 3 Zahlen aus der Matrix für jedes Quadrat. So bedeutet die 144 über dem 1. (linken) Quadrat, dass der 1. Block der 1. aus dem 1. Quadrat (1; 6; 11) ist, der 2. Block der 2. Block aus Quadrat 4 (19; 24; 19) und als 3. Block der 3. Block ebenfalls aus Quadrat 4 (34; 39; 44) eingesetzt werden muss.
Diese Kennzahlen müssen beherrscht werden. Mag ist jedoch der Meinung, dass es besser ist, das System der Einordnung in der Matrix zu kennen. Dieses System gilt nämlich für alle Matrizes für die Korrekturquadrate.
Das System ist folgendes: (Vergleiche dazu die schwarzen Zahlen der Matrix.)
Für die 1. Blöcke sind die Zahlen von 1 bis 5 von oben nach unten eingeordnet.
Bei den 2. Blöcken beginnt die Eintragung ebenfalls von oben nach unten ab dem mittleren Quadrat (hier das 3.) mit der 1. Unten angekommen geht es von oben nach unten weiter.
Die Zahlen für die 3. Blöcke sind von unten nach oben eingetragen, wobei jede 2 Zahl übersprungen wird. Das ist für Quadrat 5 die 1, für das 4. Quadrat die 3 und für das 3., dass mittlere, die 5. Dann geht es weiter mit den geraden Zahlen 2 und 4 nach oben in die Quadrate 2 und 1.
Zurück zu den 5 Korrekturquadraten. Das 1. bis 4. Quadrat ist ein teilmagisches mit der einheitlichen magischen Summe von 69. Hier haben die fallenden Diagonalen nicht die magische Summe. Nur das 5. ist magisch, da auch hier die fallende Diagonale die Summe 69 hat.
Aus den Quadraten 1 bis 4 wurde das linke Ausgangsquadrat der 6. Ordnung gebildet. (Siehe weiter unten links)
Links oben befindet sich das Quadrat 1. Rechts daneben das Quadrat 2, darunter das 3. und von dort nach links das 4. Diese Reihenfolge ist nicht bindend. Mag wird sich aber in seine weiteren Erläuterungen auf diese beziehen.
Die Quadrate links oben und rechts unten wurden um die senkrechte Achse gedreht. Dadurch kommen die richtigen Diagonalen in die fallende Diagonale des Ausgangsquadrates.
(Diese Drehung ist auch zur Quadratbildung bei Vorgabe der magischen Summe für die Einordnung eines evtl. Restes wichtig.)
Das Ausgangsquadrat (links) ist magisch. Die magische Summe von 138 ist durch 6 teilbar.
Von besonderer Bedeutung sind die blau eingefärbten Zellen mit den Zahlen 1; 34 und 19. Diese sind im Lo-Shu-Quadrat die Zellen 1 (erste Zahl im 1. Block), 4 (erste Zahl im 2. Block) und 7 (erste Zahl im 3. Block).
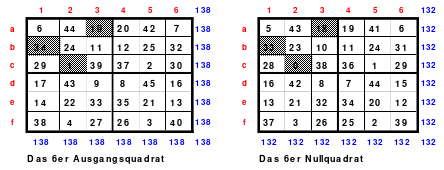
Um ein leichteres Rechnen bei der Quadratbildung zu erreichen, hat sich Mag für den Einsatz eines 6er Nullquadrates entschieden.
Ein Nullquadrat entsteht, wenn alle Zahlen im Ausgangs-, bzw. Basisquadrat um 1 reduziert werden, wodurch aus der bisher kleinsten Zahl 1 eine Null wird.
Die Zahl 34 in der Zelle 1b wird 33, und aus der 1 in der Zelle 2c wird 0. Von Bedeutung ist, dass die Zahl 19 zur 18 wird, was einer Reduzierung der Zahl in Zelle 1b um 15 entspricht.
Im Ergebnis der folgenden Arbeit fand Mag, dass eine weitere Erleichterung des Rechnens durch ein Basisquadrat möglich ist. Das Basisquadrat entstand durch die Multiplikation aller Zahlen mit der Schlüsselzahl 3 (unten links).
Die Zahl in Zelle 2c bleibt Null. Aus der Zahl 33 in Zelle 1b wird 99 und das ist auch 100-1 (!). Die Zahl in Zelle 3a wird 54, das ist auch 15*3=45 kleiner als 99 in Zelle 1b und kann leicht berechnet werden. (die 3 in 15*3=45 ist die Schlüsselzahl 3).
Die magische Summe erhöht sich ebenfalls um des 3-fache auf 396, das ist auch 400-4 und ist das 4-fache der Zahl in Zelle 1b (!).
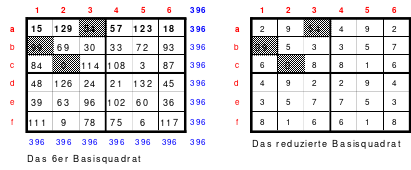
Mag schließt die bisherigen Erläuterungen ab und kommt zur praktischen Anwendung bei der Quadratbildung in Hexen 1x1, wobei Sie nur das reduzierte Basisquadrat (rechts) beachten müssen. Es enthält die 3 Startzahlen für die ersten Zahlen der 3 Blöcke des 1. Quadrates und die Zellenzahlen im Lo-Shu-Quadrat (kleine Zahlen zur Orientierung).
Des Weiteren müssen Sie die Struktur der Matrix beherrschen.
(Alle anderen vorangegangenen Erläuterungen und Berechnungen dienten lediglich der Findung einer optimalen Lösung und können vergessen werden.)
Die 3er Quadrate wurden durch verstärkte Striche kenntlich gemacht. Das dient dem besseren Verständnis und darf bei Vorführung nicht vorhanden sein.
Auch wenn das 5. Quadrat nicht Bestandteil des Ausgangsquadrates wurde, muss es bei den Berechnungen einbezogen werden.
Das Beispiel mit der Vorgabe 147
Zuerst werden die 1. Zahlen aller Blöcke berechnet. Siehe dazu das folgende linke Quadrat.
Die Vorgabe wird in Zelle 1b eingesetzt. In dieser Zelle steht im Basisquadrat die 99 (100-1). Die Differenz beträgt 147-99=48 (147-100+1=48). Um diese Differenz werden theoretisch alle Zahlen des Ausgangsquadrates erhöht, praktisch erfolgt dies ganz einfach.
Die magische Summe des Basisquadrates von 400-4 erhöht sich um das 6-fache der Differenz. Das ist 400-4+6*48=400+288-4=684 und wird über das Quadrat als die magische Summe geschrieben.
Schon ist der schwierigste Teil in der Quadratbildung erledigt!
In die Zelle 2c wird die Differenz 48 geschrieben und in die Zelle 3a 147-3*15=147-45=102 (blau schattierte Zellen).
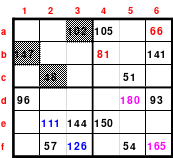
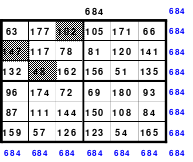
Die 1. Zahlen der 3 Blöcke in den 2.; 3. und 4. Quadrat werden unter Beachtung der Matrix durch Erhöhung um 1*3=3 bis 4*3=12 gefunden.
Die Zahlen für die 1. Blöcke sind jeweils um 1 größer, mal Schlüsselzahl 1*3=3. Folglich kommen in Zelle 5c 48+3=51, in Zelle 5f 51+3=54 und in Zelle 2f 54+3=57.
Die 1. Zahlen der 2. Blöcke sind:
Im Quadrat 2: 102+1*3=105; im Quadrat 3: 105-4*3=93; im Quadrat 4: 93+1*3=96.
Die 1. Zahlen der 3. Blöcke sind:
Im Quadrat 2: 147-2*3=141; im Quadrat 3: 141+3*3=150 und im Quadrat 4 150-2*3=144.
Diese Zahlen sind schwarz dargestellt.
(Die in Fettschrift gehaltenen Zahlen in den Formeln sind die Differenzen zwischen
den Blöcken, die der Matrix entnommen wurden.)
Alle von diesen abgeleiteten weiteren Zahlen in den Blöcken sind farblich dargestellt.
Sie erhöhen sich um jeweils 15. (Die 15 ergibt sich aus der Differenz der Zahlen in den Wechselquadraten (5) multipliziert mit der Schlüsselzahl (3).)
Im Quadrat 2 sind das die weiteren 2 Zahlen des 1. Blockes 51+15=66 und 66+15=81 (rote Zahlen).
Im Quadrat 3 sind es die 2 Zahlen des 3. Blockes 150+15=165 und 165+15=180 und im 4. Quadrat die weiteren Zahlen des 2, Blockes 96+15=111 und 111+15=126 (blaue Zahlen).
Das fertige Quadrat ist rechts abgebildet.
Sie werden zugeben, dass diese Lösung eine durchaus brauchbare ist.
Schlussfolgerungen aus der Lösung
Einige Fragen müssen noch beantwortet werden. Was ist zu tun, wenn eine größere Zahl z. B. 327 genannt wird? Denn in diesem Fall würde die Differenzzahl 228 sein, mit der nicht so leicht das 6-fache der Differenzzahl errechnet werden kann. Die Differenzzahl sollte möglichst 1- oder 2-stellig sein.
In diesen Fällen wird die Schlüsselzahl verändert und mit dieser die weiteren wichtigen Zahlen.
Diese Lösung ist einfach und wird unter Beachtung des folgend abgebildeten Quadrates und der daneben befindlichen Tabelle erklärt,
Das Quadrat ist das Basisquadrat, denn es bietet die Basis für alle anderen Vorgaben. Für die Berechnungen eines Quadrates wichtigen Zahlen sind die Vorgabe, die Zahl in Zelle 1b (Z1b), die zur Bildung der Differenzzahl von der Vorgabe abgezogen wird, weiter die Schlüsselzahl (SZ) mit Hilfe derer und der Matrix die weiteren 1. Zahlen der 12 Blöcke errechnet werden, die Multizahl (MZ) die zur Berechnung der Schlüsselzahl gebraucht wird und die magische Summe (MS), zu der das 6-fache der Differenzzahl addiert wird um die magische Summe des zu berechnenden Quadrates zu erhalten.
Diese Zahlen aus dem Basisquadrat sind die Basiszahlen (BZ) und in der 1. Zeile der Tabelle zu finden.
Die Berechnungen der erforderlichen Zahlen werden am Beispiel der genannten Vorgabe 327 erfolgen.
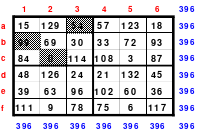
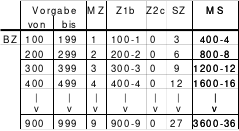
Die Vorgabe 327 gehört in die Zeile der Vorgaben 300 bis 399. Die Multizahl ist die hunderter Ziffer der Vorgabe, das ist 3. Deshalb wird die Basiszahl in Zelle 1b, das ist 99 oder auch 100-1 mit 3 multipliziert und man erhält die Zahl 300-3 die eigentlich in die Zelle 1b gehört, in der aber die Vorgabe eingesetzt wurde.
Durch Abzug (300-3) von der Vorgabe erhält man die Differenzzahl. Diese ist 327-300+3=30. Sie wird mit 6 multipliziert (30*6=180) und zur magischen Summe (1200-12) addiert. Das Ergebnis 1200+180=1380-12=1368 wird als die magische Summe über das Quadrat geschrieben. Die magische Summe 1200-12 ist die Multiplikation der Basis-MS 400-4 mit der Multizahl 3.
Die Differenzzahl wird nun in die Zelle 2c, die Nullzelle, eingegeben.
Von der Vorgabe in Zelle 1b wird 15*9=135 abgezogen und das Ergebnis 327-135=192 in die Zelle 3a eingesetzt.
Damit sind die ersten Zahlen der 3 Blöcke im Quadrat 1 vorhanden (blaue Zellen) und die übrigen 1. Zahlen der Blöcke können berechnet werden (schwarze Zahlen).
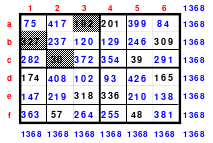
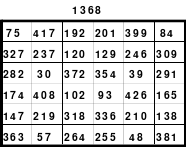
Diese Berechnung erfolgte unter Beachtung der Matrix und der Schlüsselzahl 9. Die blauen Zahlen sind die 2. und 3. Zahlen der Blöcke die um jeweils 45 (5*9) erhöht wurden.
Mit der Zunahme der Größe der Vorgabe werden auch die Berechnungen schwerer. Nicht das diese zu kompliziert wären um sie zu beherrschen, aber sie kosten mehr Zeit und das ist nicht sinnvoll. Mag hat deshalb eine Entscheidung zu dieser Frage getroffen.
Mag´s Entscheidung
Mag hat sich entschieden nur mit den Schlüsselzahlen 3; 6 und 9 zu arbeiten und entscheidet entsprechend der Größe der Vorgabe für eine der möglichen Varianten.
Er lässt sich eine Zahl kleiner 1000 nennen.
Ist diese kleiner 400, setzt er diese in die Zelle 1b ein und führt der Berechnungen wie bisher erläutert wurde aus.
Ist die Vorgabe größer 400 schreibt er diese über das Quadrat als die magische Summe und führt die Berechnungen einfach rückläufig durch. Mag wird dazu ein Beispiel bringen, da eine Vorgabe der magischen Summe an Bedingungen gebunden ist um eine Realisierung zu ermöglichen.
Eine Zahl kleiner 1000 kann auch eine 2-, oder auch eine 1-stellige Zahl sein! In diesem Fall wird die Vorgabe in die Nullzelle 2c eingetragen und als Differenzzahl behandelt. In die Zelle 1b wird die Vorgabe plus 99 (100-1) geschrieben. Alles andere läuft wie bei einer Vorgabe von 100 bis 199 ab.
Vorgabe einer magischen Summe
Mag wird die Bildung eines magischen Quadrates der 6. Ordnung bei Vorgabe der magischen Summe beschreiben. Das erfolgt jedoch in Kurzform und wahrscheinlich nur für jene verständlich, die auch die bisherigen Ausführungen verstanden haben.
Das Ausgangsquadrat ist magisch. Die magische Summe von 138 ist durch 6 teilbar. Jede Multiplikation mit einer beliebigen Schlüsselzahl ergibt eine durch 6 teilbare magische Summe. Die Differenz wird der magischen Summe 6-fach zugerechnet und ist damit ebenfalls durch 6 teilbar. Die Folge ist, dass die magische Summe insgesamt durch 6 teilbar sein muss, wenn kein Rest entstehen soll. Das ist bei der freien Wahl einer Zahl kleiner 1000 nur zufällig zu erwarten. Es wird meist ein Rest vorhanden sein.
Bei Bildung eines Quadrates der 6. Ordnung besteht das Problem in der Einordnung eines Restes. Das ist darin begründet, dass die Lösung nicht auf 6er Blöcken aufgebaut ist. Das zur Anwendung kommende sechser Quadrat besteht aus 4 Quadraten. Der gemeinsame Nenner von 4 und 6 ist 12. Es sind deshalb 12 Zellen in die Restverteilung einzubeziehen. Diese 12 Zellen müssen so eingeordnet werden, dass sie leicht zu finden sind. Sie müssen aber auch ohne große Berechnungen um den Rest erhöht werden können. Da die Lösung nur mit 12 Zellen zu erwarten ist, müssen in jede Reihe 2 dieser Zellen eingeordnet werden. Das bedeutet aber auch, dass der Rest eine gerade Zahl sein muss.
Die Lösung ist denkbar einfach. Sie musste nur gefunden werden!
Das linke Quadrat zeigt die Einordnung der zweiten Blöcke in die vier 3er-Quadrate.
Durch die um die waagerechte Achse gedrehten Quadrate 1 und 3 sind in jeder Reihe des 6er-Quadrates 2 Zahlen dieser Blöcke enthalten.
Eine der ersten Zahlen dieser Blöcke befindet sich in der Zelle 3a. Die Zahl für diese Zelle wird bekanntlich berechnet durch Abzug des Wertes 15*SZ, bei einer Schlüsselzahl 3 ist das 45. Alle anderen 1. Zahlen der 2. Blöcke werden von dieser Zelle rechnerisch abgeleitet. Es ist ein Leichtes bei der Berechnung der Zahl für Zelle 3a dieser den halben Rest zuzuschlagen. Er wird dann ohne weitere Beachtung in die anderen Zahlen der 2. Blöcke übertragen.
Es bleibt die Frage nach einer geraden Vorgabe.
Bei Nennung einer ungeraden Vorgabe wendet sich Mag an das Publikum und bittet mit den Worten “Machen wir das noch etwas komplizierter und addieren eine Primzahl dazu” um Nennung einer 1- oder 2-stelligen Primzahl. Findet sich keiner, so schlägt er ein paar zur Wahl vor und bittet einen Zuschauer die Auswahl zu treffen.
Primzahlen sind ungerade Zahlen und die Vorgabe wird damit eine gerade Zahl.
Wird eine gerade Zahl als Primzahl genannt, lehnt er diese als keine Primzahl ab.
Wird eine ungerade Zahl genannt die keine Primzahl ist, so spielt das keine Rolle.
Erkennt Mag, dass die Zahl keine Primzahl ist, so sollte er darauf hinweisen und trotzdem der Vorgabe zurechnen.
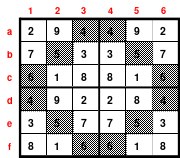
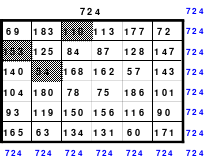
Die Bildung eines magischen 6er-Quadrates bei Vorgabe einer Summe ist denkbar einfach. Sie läuft praktisch rückwärts wie bisher gerechnet ab. Das kann am besten an einem Beispiel gezeigt werden.
Mag führt die Berechnungen grundsätzlich unter Nutzung des Basisquadrates mit der Schlüsselzahl 3 durch. Bei Vorgaben kleiner 1000 entstehen dabei bis auf sehr seltene Ausnahmen nur 2-stellige Differenzzahlen. Die größtmögliche Ausnahme wäre Vorgabe 999+97 als 2-stellige Primzahl mit dem Ergebnis 116 als Differenzzahl und 4 als Rest.
Als Vorgabe wurde 713 genannt Es wird um eine Primzahl gebeten. Es wird 11 gesagt. Die Vorgabe erhöht sich auf die gerade Zahl 713+11=724.
Von dieser wird die magische Summe des Basisquadrates in Höhe von 400-4 abgezogen und das Ergebnis ist 724-400+4=328.
Die 328 wird durch 6 dividiert und das Ergebnis ist 328/6=54-Rest 4. Die 54 wird in die Zelle 1c eingesetzt und der Rest 4 gemerkt. (Die Division erfolgt von links nach rechts. weshalb die Zwischenergebnisse zuerst 5, dann 4 sofort in die Zelle 2c eingetragen werden können.)
In die Zelle 1b wird der Wert aus Zelle 2c, das ist 54, um 100-1 erhöht und das Ergebnis 54+100-1=153 eingetragen.
Nun kann auch die 3. Startzahl für Zelle 3a berechnet werden. Sie ist um 45 kleiner als die Zahl in Zelle 1b. Dieser wird aber auch der halbe Rest von 4/2=2 zugeschlagen. Das Ergebnis ist 153-45+2=110.
Alle weiteren Berechnungen werden wie bei der Zahlenvorgabe für die Zelle 1b ermittelt.
Das fertige Quadrat ist oben rechts abgebildet.
Eine Nachbetrachtung
Dem aufmerksamen Zuschauer könnten die symmetrische Einordnung der Zahlen und deren Differenzen von 3 und 6 auffallen. (Haben Sie es auch erkannt?)
Das muss in Kauf genommen werden, wird aber bei Einsatz einer größeren Schlüsselzahl (6 oder 9) stark abgeschwächt. In der Regel wird als Zahl kleiner 1000 kaum eine Zahl kleiner 2- oder 3-hundert genannt.
Bei der Vorgabe der magischen Summe kann die Auffälligkeit durch Vorgaben größer 1000 verhindert werden. In diesen Fällen wird von der magischen Summe (800-8) und wenn sie größer 1200 ist auch (1200-12) abgezogen. Die Schlüsselzahl wird dann 6 bzw. 9 groß und die Zahl in Zelle 1b = Differenz+(200-2) bzw. +(300-3).
Bei einer Vorgabe von 100 bis 400 kann diese auch in die Nullzelle (2c) eingegeben werden. In die Zelle 1b wird dann eine um 100-1 größere Zahl eingesetzt. Durch diese Manipulation wird die Schlüsselzahl 6 oder 9.
Alle weiteren Veränderungen ergeben sich aus diesen Zahlen.
(Aber machen Sie es sich nicht schwerer als notwendig und begnügen Sie sich mit einer Vorgabe kleiner 1000 und variieren Sie nicht zwischen der Vorgabe in Zelle 1b oder 2c.)
Mag gefällt die Bildung einer geraden Vorgabe durch Addition einer Primzahl nicht. Sie kommt ihm etwas zu plump daher. Auch kann es zu Problemen mit der Primzahl kommen, denn nicht jeder kennt welche. Es steht auch die Frage „Was soll das?“ im Raum.
Mag bevorzugt deshalb eine bessere Variante, mit der auch eine Vorgabe größer 1000 leicht mit der Multiplikation einzelner Ziffern erreicht werden kann
Mag wendet sich an das Publikum mit den Worten:
„Ich benötige eine größere Zahl, die aber nicht einer von Ihnen nennen soll, sondern gemeinsam gebildet wird. Bitte nennen Sie mir eine Ziffer von 1 bis 9.“
Dazu fordert er einen Zuschauer aus der Mitte mit einer Handbewegung auf. Es wird 7 gerufen, die Mag an die Tafel schreibt und dahinter das Multiplikationszeichen (x). Dann wendet er sich nach links, wo als Ziffer 4 genannt wird. Auch diese schreibt Mag an die Tafel. Weiter werden die Ziffern 7, 5 und 3 genannt.
An der Tafel steht die Formel
7x4x7x5x3=2940
Mag hat das Ergebnis mit 2940 errechnet.
(7*7= (50-1) *4= (200-4) *5=1000-20) *3=3000-60=2940)
Er hätte auch einen Zuschauer bitten können, dies mittels seines Smartphon zu berechnen.
Bei dieser Form der Zahlenbildung spekuliert Mag darauf, dass folgende Regeln zum Tragen kommen:
Ist eine der Ziffern eine Gerade (2, 4, 6 oder 8) wird das Ergebnis eine gerade Zahl. Das wurde mit der 4 erfüllt. Die Erfragung von Ziffern hätte mit der 5 beendet werden können. Das Ergebnis wäre dann 980 gewesen. Mag wollte aber mehr erreichen mit der Regel:
Ist eine Ziffer die 6, oder wird eine gerade Ziffer (2, 4, 8) und eine durch 3 teilbare Ziffer (3, 6, 9) genannt, so ist das Ergebnis durch 6 teilbar und ein Rest wird ausgeschlossen. Das wurde mit den Ziffern 4 und 3 erreicht. Allerdings ist die Zahl 2940 groß, was aber beherrscht werden kann.
Um die Schlüsselzahl nicht größer als 9 festzulegen, ergeben sich die nachstehenden Berechnungen:
2940-(1200-12) = 1740+12 =1752, Differenzzahl = 1752/6=292, Rest = 0, Schlüsselzahl =9
Auch die nachfolgende Berechnung wäre möglich, allerdings auch etwas ungünstiger:
2940-(2400-24) = 540+24 = 564, Differenzzahl = 564/6=94, Rest =0, Schlüsselzahl =18
Natürlich kann auch wie vorgeschlagen mit der Schlüsselzahl 3 gerechnet werden, denn die Vorgabe ist ja größer 400-4. Das wäre folgende Berechnung:
2940-(400-4) = 2540+4 = 2544. Differenzzahl = 2544/6=424, Schlüsselzahl =3
Die beschriebenen Berechnungen bei der Quadratbildung erfolgten zum besseren Verständnis in einer logischen Reihenfolge. Bei Vorführungen sollten die Eintragungen in das Quadrat in einer nicht erkennbaren Ordnung erfolgen. So wäre z. B. nach Nennung einer Vorgabe für Zelle 1b und der Berechnung der magischen Summe eine sofortige Berechnung der Zahl für Zelle 7 im 3. Quadrat (4e) mit anschließender Eintragung der 2 weiteren Zahlen für die Zellen 8 und 9 im 3. Quadrat (6f und 5d) möglich. In dieser Art und Weise können Sie beliebig variieren.
Die von Mag gefundene Lösung bei der Berechnung eines Quadrates der 6. Ordnung im Hexen 1x1 muss als sehr gelungen bewertet werden. Besonders die Bildung des Quadrates bei Vorgabe der magischen Summe zeigt, dass die einzelnen Lösungswege eine in sich geschlossene und harmonische Einheit bilden. Die Berechnungen sind rationell überdacht und einfach. Sie sind ohne große mathematische Kenntnisse realisierbar. Ein großer Vorteil ist, dass die Vorgaben nach unten nicht begrenzt werden müssen.
Trotz der nicht erwarteten rationellen Lösung, wird Mag seine bisherigen Aussagen zu den 6er Quadraten nicht ändern.
Eine Überarbeitung würde weitere Zeit benötigen, die Mag nicht mehr aufbringen kann.
6.6. Quadrate der 7. Ordnung
6.6.1. Das Heptaquadrat
Auch wenn Mag mehrfach betont hat, dass sich die Rechenkunst mit magischen Quadraten auf Quadrate bis zur 5. Ordnung beschränken sollte wird er nachfolgend auch einige Beispiele aufzeigen, wie auch Quadrate der 7. Ordnung in die Rechenkunst einbezogen werden können, was aber nur begrenzt erfolgen sollte. Ein Quadrat der 7. Ordnung mit 49 Zellen hat praktisch die doppelte Anzahl von Zellen eines Quadrats der 5. Ordnung mit nur 25 Zellen. Folglich wird für deren Abarbeitung auch die zweifache Zeit gegenüber dem 5er Quadrat benötigt. Sogar noch mehr, da die Arbeit mit einem 7er Quadrat größere Vorgaben erfordern und eine wesentlich höhere Konzentration dem Vorführenden abverlangen.
Wenn Mag nun doch ein Quadrat der 7. Ordnung in seine Ausführungen aufnimmt, dann aus einigen Gründen.
Durch eine Darbietung “Klein gegen Groß” im Fernsehen, wo ein Quadrat der 8. Ordnung berechnet werden musste, ist das Interesse auch an großen Quadraten gewachsen und wird oft vom Rechenkünstler abgefordert. Deshalb hat Mag auch 2 Beispiele mit einem Quadrat der 8. Ordnung als gesonderten Abschnitt im Hexe 1x1 aufgenommen. Mit dem 7er Quadrat wird nun auch die Lücke nach dem 5er Quadrat geschlossen. Es fehlt dann nur noch das 6er Quadrat, was sich allerdings nicht für die Rechenkunst mit magischen Quadraten eignet.
Nochmals zur Festigung des Wissens, das Wesentliche zum Heptaquadrat, einem pandiagonalen Primquadrat der 7. Ordnung.
Das Heptaquadrat ist ein 49-zelliges Quadrat, das mittels der Springermethode erstellt wurde. Es besteht aus 7 Blöcken mit jeweils 7 Zahlen. Die Abstände zwischen den Zahlen innerhalb des Blockes sind 2 Zellen nach rechts und 1 Zelle nach unten. Der Übergang von Block zu Block ist 2 Zellen nach unten.
In jeder Reihe (Spalte, Zeile, Haupt- und gebrochene Diagonale) befindet sich je eine Zahl jedes Blockes. Dabei sind diese jeweils eine 1., 2. 3. ...... und 7. Zahl eines Blockes. Das Quadrat ist damit ein 100-prozentig homogenes.
Die mittlere Zellenzahl ist 25 und die magische Summe 175.
Da das Quadrat ein homogenes ist, können Zeilen und/oder Spalten beliebig versetzt werden, wobei das Quadrat immer ein magisches und pandiagonales bleibt.
Das bedeutet auch, dass jede Zahl im Quadrat jede Position innerhalb des Quadrates einnehmen kann.
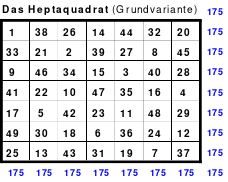
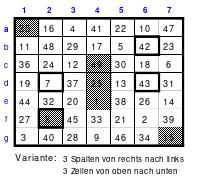
Eine Analyse
mit der Variante, die rechts abgebildet ist. Es wurden 3 Spalten von rechts nach links und 3 Zeilen von oben nach unten versetzt. Diese Veränderung erleichtert eine Analyse und lässt die Aussagen leichter erkennen.
Auf eine Besonderheit muss hingewiesen werden. Im Heptaquadrat befinden sich die größte Zahl 49, die mittlere Zahl 25 und die kleinste Zahl 1 in nur einer Spalte und das sogar zusammenhängend untereinander.
Eine weitere und wichtige Eigenschaft ist die Anordnung der Duos.
Beide Zahlen eines Duos befinden sich symmetrisch zur mittleren, der Zelle 25. So z. B. die 29 in Zelle 3b und die 21 in Zelle 5f.
Für das Hexen 1x1 sind neben dem Duo 1/49 vor allem die Duos 15/35, 8/42 und 7/43 wichtig. Diese Duos bestehen jeweils aus einer ersten und letzten Zahl eines Duos. (Siehe farbig eingerahmte Duos)
Noch bedeutungsvoller sind die schattierten Duos. Sie werden in einigen Fällen der Quadratbildungen benötigt und haben eine Signalfunktion. Sie befinden sich in der gleichen Zeile, Spalte oder Diagonalen in der sich auch die Zelle 25 befindet und können deshalb leicht lokalisiert werden.
(Dazu werden in den einzelnen Experimenten noch Aussagen getroffen)
Die Duosumme beträgt das 2-fache der mittleren Zahl 25, das ist 50. Das gilt auch, wenn die Zahl in Zelle 25 z. B. auf 72 erhöht wird. Dann muss die Duosumme 2*72 = 144 sein, damit es magisch bleibt.
Rechenexperimente mit dem Heptaquadrat
In allen Fällen, auch beim Experiment “Einfach Clever”, kann die Zelle vorgegeben werden, mit der begonnen werden soll. Das stellt keine nennenswert höheren Anforderungen an den Vorführenden und sollte deshalb genutzt werden. Aus der Sicht der Zuschauer bedeutet es eine weitere Erschwernis bei der Lösung der gestellten Aufgabe.
Mag wird Sie über folgende Rechenexperimente informieren:
Bildung eines magischen Quadrates bei Vorgabe einer mehrstelligen Zahl für eine Zelle.
Bildung eines magischen Quadrates bei Vorgabe einer mehrstelligen Zahl als magische Summe.
Bildung eines magischen Quadrates bei Vorgabe mehrerer Zahlen.
Bei den folgenden Experimenten der “Hohen Schule” werden die Zahlen zeilenweise eingetragen.
Es sind die Experimente:
Einfach Clever, eine leichte, raffinierte Lösung, wie sie bereits bei den Quadraten der 5. Ordnung zur Anwendung kam.
Das Königsquadrat, ein Rechenexperiment der besonderen Klasse mit zwei Sternen für das ein ganz besonderes 7er Quadrat gefunden werden musste. Die Anforderungen an das Rechnen sind höher als bei den vorangegangenen Exprimenten. Auch hier wird der gleiche Lösungsweg wie bei den Quadraten der 5. Ordnung genutzt.
6.6.2. Zahlenvorgabe *
Mag bittet um eine nicht zu kleine 3-stellige Zahl. Es wird 403 genannt.
Weiter bittet er um Angabe, mit welcher Zelle begonnen werden soll. Es wird die 3. Zelle in der vorletzten Zeile gewählt, in die Mag die 403 einträgt.
Anschließend schreibt er über das Quadrat die Zahl 2015.
Es ist die Startsituation wie im linken Quadrat gezeigt wird.
Danach schreibt er in die Zellen in einer scheinbar unregelmäßigen Ordnung Zahlen ein, bis das Quadrat fertig ist. Es ist die rechte Abbildung.
Das Quadrat ist magisch (und sogar pandiagonal).
Alle Reihen haben als Summe die magische Summe 2015, die Mag vorher über das Quadrat geschrieben hat.
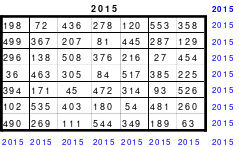
Die Lösung
Mag wird 2 möglich Lösungen beschreiben. Die Lösungsvariante 1 “Über Umwege” und die Lösungsvariante 2 - “Die Geradlinige”. Die Erstellung des rechten Quadrates erfolgte mittels der Variante 1, die Mag nachfolgend detailliert beschreibt.
Lösungsvariante 1 - Über Umwege
Im Allgemeinen wird bei Primquadraten die Tatsache genutzt, dass die magische Summe das O-fache der mittleren Zelle beträgt, wobei O die Ordnungszahl ist.
Das war beim Pentaquadrat: Mittlere Zelle 13*5 = 65, die magische Summe.
Beim Heptaquadrat, ein Quadrat der 7. Ordnung, ist das 25*7 = 175 als magische Summe.
Diese Regel wird in der Rechenkunst mit magischen Quadraten genutzt.
Bei Einsatz des Heptaquadrates wäre das als Beispiel:
Wird eine Zahl als magische Summe vorgegeben, so wird diese durch 7 geteilt und man erhält die Zahl für Zelle 25. Die Division erfolgt von links nach rechts.
Wird eine Zahl für eine Zelle vorgegeben, so wird diese in die mittlere Zelle 25 eingetragen und durch Multiplizierung mit der Ordnungszahl 7 die magische Summe errechnet. Beim Pentaquadrat wurde die Multiplikation durch einen kleinen Trick erleichtert. Die Zahl in Zelle 13 wurde mit 10 multipliziert und dann durch 2 dividiert, denn x*5 ist auch x*10/2. So war es möglich, die Summe von links nach rechts zu berechnen und auch so als magische Summe über das Quadrat zu schreiben.
Solch ein Trick ist beim Heptaquadrat nicht möglich. Folglich muss die Multiplikation im Kopf erfolgen. Das dürfte für einen guten Rechner keine Hürde sein, aber nicht jeder kann sich für einen solchen halten. Sie können sich ja testen, indem Sie für die Zahl 748 das 7-fache berechnen. Mehr als 10 sec. werden Ihnen nicht zugestanden, denn eine längere Pause sollte dem Publikum nicht zugemutet werden.
Bleibt nur die schulmäßige Berechnung von rechts nach links, was auch so angeschrieben wird.
Diese Form ist für einen “Rechenkünstler” nicht akzeptabel. Es kratzt an seinem Image.
Mag hat einen Weg gefunden, wie die Berechnungen in einer einfachen Art erfolgen können. Dieser Weg ist ein “Umweg”, der über die Zelle 35 führt. Mit weiteren Einzelheiten macht Sie Mag in einem Beispiel vertraut.
Vorher jedoch nochmals ein paar Bemerkungen zu den Starterzahlen und deren Einordnung.
Wie schon gesagt, wird mit der Zelle 35 begonnen. Da das Heptaquadrat ein pandiagonales ist, kann auch die Zelle bestimmt werden mit der begonnen werden soll. In diese wird die Vorgabe eingesetzt. Die anderen Starterzahlen werden in der Reihenfolge 25 - 15 - 1 - 8 - 49 berechnet. Diese können leicht gefunden werden. Von der Zelle 35 aus 3 Zellen nach rechts und 3 Zellen nach unten zur Zelle 25. Von dort wieder 3 Zellen nach rechts und 3 Zellen nach unten zur Zelle 15.
Das sind in beiden Fällen auch 3 Zellen diagonal nach rechts unten.
Die Zelle 15 befindet sich dann auch 1 Zelle nach links oben von Zelle 35, was einfacher ist.
Die Zelle 1 (die kleinste) befindet sich unter der Zelle 25 (der mittleren) und die Zelle 49 (die größte) über der Zelle 25. Diese Zahlen befinden sich aufsteigend in der gleichen Spalte.
Nach diesen einfach zu merkenden Regeln sind die entsprechenden Zellen auch in einem veränderten Quadrat leicht zu finden. Das rechte Quadrat ist ein verändertes, mit der 35 in der geforderten Position, 3. Zelle in der vorletzten Zeile. Das ist die Zelle 3f.
(Die blauen Zahlen und Buchstaben dienen nur der Erläuterung und werden bei Vorführungen weggelassen.)
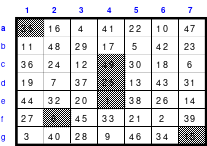
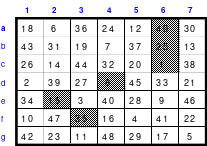
Die nächste Abbildung zeigt die Einordnung der Starterzahlen in die Duokette.
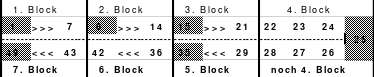Die Duokette
Die 35, in der sich die Vorgabe befindet, ist die letzte im 5. Block. Von dieser müssen in absteigender Form die Zellen 34 bis 29 berechnet werden.
Die mittlere Zelle 25 wird als erstes berechnet und befindet sich in der Mitte des 4. Blocks. Von dort müssen die Zahlen für die Zellen 23 bis 22 absteigend und die Zahlen für die Zellen 26 bis 28 aufsteigend berechnet werden.
Die 15 ist die 1. Zahl im 3. Block. Die Zahlen bis 21 sind aufsteigende.
Die Zahlen von 1 bis 7 und 8 bis 14 werden aufsteigend errechnet und
die Zahlen von 49 bis 36 absteigend.
Alle Duos haben die Duosumme 50, das ist das Doppelte von 25, der mittleren Zelle.
Doch nun zur Lösung
Mag bittet um eine 3-stellige Zahl größer 400.
(Es kann auch eine größere 3-steliige oder eine 3-stellige Zahl aus dem oberen Bereich erfragt werden. 400 ist die kleinstmögliche, aufgerundete Zahl, die den Einsatz der Schlüsselzahlen 9 und 7 zulässt.)
Es wird 403 gewählt.
Mag bittet um die Bestimmung der Zelle, mit der begonnen werden soll. Die 3. Zelle in der vorletzten Zeile wird gefordert, in die Mag die 403 einsetzt.
Sofort berechnet er die magische Summe.
Da 35 ein Fünftel von der magischen Summe des Grundquadrates, 175, ist, multipliziert er die 403 mit 5. Dabei wendet er den bekannten Trick an, indem er im Gedanken eine 0 anhängt und die 4030 durch 2 teilt. Die Teilung erfolgt von links nach rechts und Mag kann jede berechnet Ziffer sofort hintereinander über das Quadrat schreiben. Das ist 2..0..1..5 (2015), die magische Summe.
Nach Ortung der Zelle 25 berechnet er die Zahl für diese.
Da die mittlere Zahl 25 ein siebentel von 175 ist, dividiert Mag die magische Summe 2015 durch 7, was ebenfalls von links nach rechts erfolgt. So können die Ziffern auch hintereinander in die Zelle eingesetzt werden. Die fertige Zahl ist 287, Rest 6. Den Rest muss man sich merken.
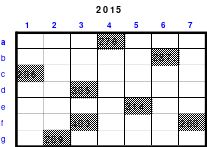
Es wird empfohlen, vor der Berechnung der weiteren Startzahlen die 3 auf- und 3 absteigenden Zahlen des Blockes 4 zu berechnen. Das dient der Übersicht und ist
zugleich eine Kaschierung der Anordnung der anderen Startzahlen, besonders der übereinander angeordneten Zahlen der 1., 25. und 49. Zelle.
Von der Zahl in Zelle 25 werden weitere Startzahlen abgeleitet. Um Verwechslungen zu vermeiden, ist eine heimliche Kennzeichnung dieser Zahl ratsam. Mag hat die mittlere Zahl 257 mit einem Punkt versehen.
Der erreichte Zwischenstand ist im linken Quadrat erkennbar. Die Schattierungen dienen dabei einem besseren Erkennen der Berechnungen.
Das rechte Quadrat zeigt die Situation, wie sie vom Publikum gesehen wird.
Jetzt folgt der schwerste Teil der Berechnungen, die der Zahl für Zelle 15.
Die 15 bildet mit der 35 ein Duo mit der Duosumme 50, was das Doppelte der mittleren Zelle 25 ist.
Es wird die Zahl in Zelle 25 verdoppelt und von diesem Ergebnis die Zahl in Zelle 35, die Vorgabe, abgezogen. Hier muss jeder seine eigene Methode anwenden.
Mag rechnet: 290*2 = 580 - 6 = 574 - 400 = 174 - 3 = 171
Die Zahl für Zelle 1 wird ganz einfach ermittelt. Da die 1 um 14 kleiner als die Zahl 15 ist, muss das 14+1 = 15-fache der Schlüsselzahl von der Zahl in Zelle 15 abgezogen werden. Die +1 sichert, dass die Zahl in Zelle 1 nicht Null wird. Es wird die Schlüsselzahl 9 oder 7 gewählt. Um nicht zu eng zu agieren und etwas Sicherheit zu haben, wird der Einfachheit halber mit 10 gerechnet.
Die Zahl für Zelle 1 wird damit 171-15*10 = 21. Dem Block 1 muss jedoch noch der Rest zugeschlagen werden, weshalb die Zahl für Zelle 1 = 21+6 = 27 wird.
Die Startzahl in Zelle 8 wird aus Sicherheit eingerichtet. Sie soll verhindern, dass bei der Eintragung der Zahlen in die aufsteigende Zahlenreihe der Blöcke 1 und 2 nicht versehentlich der Rest mit in den Block 2 übertragen wird.
Die Zahl für Zelle 8 wird von der Zahl in Zelle 1 abgeleitet. Sie ist um das 7-fache der Schlüsselzahl größer, jedoch muss der Rest wieder abgezogen werden.
Die Zahl für Zelle 8 ist dann 27+7*9 = 27+63 = 90, nach Abzug des Restes von 6 ist die Zahl mit 84 gefunden.
Die Zelle 8 befindet sich einen Linkssprung von Zelle 1 aus.
Der Linkssprung ist 2 nach links und 1 nach unten.
Nach dieser Regel können alle um die Ordnungszahl größeren Zellen gefunden werden. So führt der Linkssprung auch von der Zelle 8 zur Zelle 15, denn beide sind erste Zahlen ihrer Blöcke.
Das so erreichte Zwischenergebnis ist in den folgenden Quadraten zu erkennen.
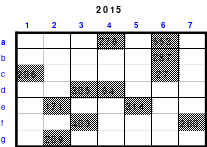
Damit sind auch die Hauptaufgaben erledigt.
Es kann mit der zügigen Eintragung aller restlichen Zahlen begonnen werden.
Die Abarbeitung der absteigenden Zahlen sollte als erstes vorgenommen werden, das sind die Startzahlen 403 in Zelle 35 (3f) und 553 in Zelle 49 (6a).
Von diesen aus wird im Rückwärtssprung (1 nach oben und 2 nach links) die Zelle mit der um 1 kleineren Zellenzahl angesteuert und eine um die Schlüsselzahl reduzierte Zahl eingesetzt. Das ist als Beispiel von der Startzahl 403 in Zelle 35 (3f) zur Zelle 34 (1e) in die 403-9 = 394 eingeschrieben wird. So wird weiter verfahren bis zur Zahl 349 in Zelle 5g. Von dort ist ein weiterer Sprung nicht möglich, da die Zelle 3f bereits belegt ist. Das ist das Signal, dass der Block fertig ist. (grün schattiert).
Genau so wird ab der Startzahl 553 verfahren. (Zyan schattiert) Nach erreichen der Zahl 499 in Zelle 1b kann ebenfalls nicht weiter gesprungen werden, denn die Zelle 6a ist belegt. Damit ist man informiert, dass der Block fertig ist und zum nächsten übergegangen werden muss. Das ist 2 Zellen nach oben zur Zelle 1g in die 490 kommt. Weiter in Rückwärtssprüngen bis zur Zelle 3a, von der aus nicht weiter gesprungen werden kann. Auch ein Übergang zum nächsten Block ist nicht möglich, da die Zelle 3f ebenfalls eine Zahl enthält. Alle Rückwärtssprünge sind erledigt und im linken Quadrat als Zwischenergebnis dargestellt.
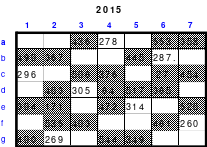
Mag hat bewusst die Ausführungen sehr ausführlich gemacht, obwohl die Regeln bereits aus den vorangegangenen Erläuterungen bestens bekannt sein müssten. Er hat es getan, um nochmals zu zeigen, dass Sie sich keinerlei Zellenzahlen merken müssen, auch nicht die blauen Zellenbezeichnungen in den linken Quadraten.
Was Sie wissen müssen, ist die Einordnung der Startzahlen zueinander und die Berechnung der Startzahlen. Alles andere läuft nach den bekannten Regeln ab. Sie müssen auch nicht mitzählen, ob der Block fertig ist. Sie erhalten dazu stets die erforderlichen Informationen in Form bereits belegter Zellen. Daraus sollen Sie erkennen. dass die Bildung größerer Quadrate keine wesentlich höheren Anforderungen an den Vorführenden stellen und damit auch für Sie von Interesse sein dürfte.
Als nächstes sind die restlichen Zahlen der aufsteigenden Zahlenreihen zu bearbeiten. Die Zellen werden im Normalsprung, 2 nach rechts und 1 nach unten, gefunden. Das ist ab der Startzahl 171 (Zelle 15) und 27 (Zelle 1).
Ab Startzahl 171 endet die Eintragung mit der Zahl 225. Von dort kann nicht weiter gesprungen werden und auch kein Übergang erfolgen. Der Block ist fertig. (blau schattiert)
Ab der Startzahl 27 geht es bis zur Zahl 81. Von dort kann nicht mehr gesprungen werden, denn die entsprechende Zelle ist mit der Zahl 27 belegt.
Auch ein Übergang ist nicht machbar, weil diese Zelle die 84 enthält. Für Sie ist das die Erinnerung daran, dass ab der Zelle mit der Zahl 84 ein neuer Block beginnt, der nicht mehr mit den Rest 6 belastet werden darf. Das ist auch daran zu erkennen, dass die Zelle nach einem Sprung von der 84 aus, leer ist. In diese kommt dann die Zahl 84+9= 93. Nach Fertigstellung dieses letzten Blockes (gelb schattiert) ist das Quadrat fertig.
Es ist magisch mit der magischen Summe von 2015.
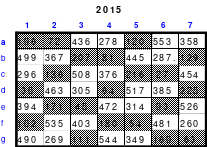
Eine Nachbetrachtung
Die folgende Tabelle zeigt die einzelnen Rechenoperationen zur Berechnung der Startzahlen, bei einer Schlüsselzahl von 9 und grenzwertigen Vorgaben von geforderten 3-stelligen Zahlen größer 400.
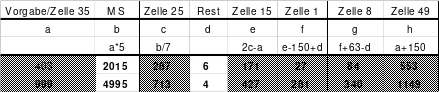
Die Zahlen für die magische Summe, Zelle 25 und 15 werden aus der Vorgabe abgeleitet und sind deshalb unveränderlich. Die Zahl für Zelle 49 ist nach oben offen und kann aus der Betrachtung ausgeklammert werden. Nicht so die Zahl für Zelle 15. Von dieser muss 10-mal die Schlüsselzahl abgezogen werden, das ist rd. 150 bei der Schlüsselzahl 9.
Die Ergebnisse mit der Vorgabe 403 zeigen, dass eine kleinere Vorgabe nicht möglich ist.
Bei der Vorgabe 999 erlauben die Ergebnisse auch den Einsatz einer größeren Schlüsselzahl z. B. 19. Die Differenz zwischen den Zellen 25 und 15 ist 10 und lässt eine Differenz zwischen den Zahlen von 10*19 = 190, aufgerundet 200 zu.
Auch der Abzug von 15*19 = 281, rd. 300 von Zelle 15, zur Ermittlung der Zahl für Zelle 1, ist möglich.
(Die in der Tabelle angegebenen +-150 (Spalte f und h) stellen das Minimum bei Verwendung der Schlüsselzahl 9 dar und müssen nicht zwingend erhöht werden.)
Die 7 als Schlüsselzahl ist unbedenklich einsetzbar.
Eine analoge Berechnung ist der Umweg über die Zelle 7. Wenn 25*7 die magische Summe ist, dann ist sie es auch mit 7*25. Wird die Zahlenvorgabe in die Zelle 7 eingesetzt, so ist das 25-fache der Vorgabe die magische Summe. Anstelle der 25 wird mit 100/4 gerechnet. An die Vorgabe werden gedanklich 2 Nullen angehängt und durch 4 geteilt.
Aus einer Vorgabe von 101 wird die magische Summe 10100/4 = 2525 errechnet und die mittlere Zahl für Zelle 25 mit 2525/7 = 360, Rest 5.
Wird über die Zelle 7 gerechnet, muss nicht um eine “nicht zu kleine 3-stellige Zahl” gebeten werden, sondern nur um eine 3-stellige, denn bei der kleinsten 3-stelligen Zahl kann 9 als Schlüsselzahl eingesetzt werden.
(Für die Zelle 1 verbleibt mindestes 100-6*9 = 37.
Ehe die übrigen Zellen mit Zahlen versehen werden, muss noch die Zahl für die 2. Partnerzelle des Duos 7/43 berechnet werden. Die 2. Duozelle ist die Zelle 43, die erste im letzten, den 7. Block. Die Zahl für Zelle 43 ist Duosumme minus Zahl in Zelle 7.
Die Zelle 7 ist die letzte im 1, Block, weshalb die restlichen Zahlen des Blockes absteigend berechnet werden müssen. Die Zahlen für die übrigen Zellen werden, ausgehend von der Zelle 25, absteigend bis Zelle 8 und aufsteigen bis Zelle 42 berechnet.
Einem der aufsteigenden Blöcke muss der Rest zugeschlagen werden. Günstig ist der letzte Block mit der getrennt zu berechnenden Zahl für Zelle 43, die 1. im 7., den letzten Block.
Vorteilhaft ist, dass zwischen den Umwegzellen 7 oder 35 gewählt werden kann. So wird bei einer Vorgabe größer 400 die Zelle 35 für den Umweg festgelegt, ansonsten die Zelle7.
2. Variante 2 - Die Geradlinige
Man lernt nie aus, auch Mag nicht!
Hatte er doch die Variante 1 vor allem deshalb entwickelt, weil die Multiplikation einer 3-stelligen Zahl mit 7 angeblich nur schwer durch Kopfrechnen zu lösen sei.
Bei der Variante 1 hatte Mag die 403 als Vorgabe einer Zahl für eine Zelle gewählt. Er wollte demonstrieren, dass mit einer Vorgabe 400 eine Berechnung eines 7er Quadrates noch möglich ist, ohne dass doppelte Zahlen entstehen und eine zufrieden stellende Verteilung der 49 Zahlen bei einer Schlüsselzahl 9 erfolgt.
Als er die Vorgabe 403 in die Zelle 35 einsetzte und die magische Summe mit der Formel Vorgabe * 10 / 2 = 403 * 10 = 4030 / 2 = 2015 berechnete, erkannte er, dass das Ergebnis auch erreicht werden kann, wenn 4*5 = 20 und 3*5 = 15 zur Zahl 2015 zusammengefügt wird. Das geht auch mit dem Faktor 7. Bei Einsatz der 403 in die Zelle 25 würde die magische Summe 4*7 = 28 und 3*7 = 21 zusammen 2821 ergeben.
Das Ganze ist natürlich keine großartige Erkenntnis und allgemein bekannt. Auch geht das nur, wenn die mittlere Ziffer der 3-stelligen Zahl eine Null ist. Eine solche Vorgabe wird sehr wahrscheinlich äußerst selten, wenn überhaupt, genannt. Also was soll das?
Ganz einfach! Mag hat darin eine leichte Berechnung der magischen Summe bei Einsatz einer Vorgabe in die Zelle 25 erkannt, die sicherlich auch nichts Neues ist.
Hier die Erklärung dazu:
Als Vorgabe wurde 748 genannt, die in eine gewählte Zelle eingesetzt wurde.
Diese Zelle ist für Mag die Zelle 25 und die magische Summe das 7-fache von 748.
Mag rechnet: Erste Ziffer 7*7 = 49 und dritte Ziffer 8*7 = 56 zusammengefügt 4956. Davon wird die letzte Ziffer abgekoppelt und es verbleibt 495.
Zu dieser wird das 2-stellige Produkt aus der mittleren Ziffer 4*7 = 28 addiert und man erhält 495+28 = 523, die über das Quadrat geschrieben wird, jedoch wird noch die abgekoppelte Ziffer 6 als letzte Ziffer angehängt und die magische Summe ist mit 5236 gefunden.
Diese Art zu rechnen ist bestimmt nicht schwerer als die mit mehreren 3-stelligen Zahlen in Variante 1.
Es muss dabei beachtet werden, dass die Multiplikation der letzten Ziffer mit 7 ein 2-stelliges Ergebnis sein muss. Bei einer letzten Ziffer 0 wird 0*7 = 00 und bei einer 1 wird 1*7 = 07.
Auf eine bildliche Darstellung eines 7er Quadrates mit der Vorgabe 748 in eine beliebige Zelle wird verzichtet. Die Regeln dazu wurden bereits mehrfach beschrieben.
Im Beispiel wäre das: Über das Quadrat wird die magische Summe wie berechnet
von 5236 geschrieben.
Die gewählte Zelle ist die Zelle 25 mit der Vorgabe 748
Die max. Schlüsselzahl ist 7*4 = 28 >> gewählt 19
(7 sind die Hunderter der Vorgabe 748. Die 4 ergibt sich aus 100/25, wobei 25 die mittlere Zellenzahl ist.)
Ausgehend von der Zelle mit der Vorgabe, werden die auf- und absteigenden Zahlen nacheinander berechnet und nach den Springerregeln eingesetzt.
6.6.3. Summenvorgabe
Die Vorgabe einer magischen Summe und die Bildung eines magischen Quadrates der 7. Ordnung, mit der vorgegebenen magischen Summe, wurde bereits im Abschnitt 2. “Zahlenvorgabe” ausführlich beschrieben.
Mag wird deshalb nur eine kurze Erläuterung als Erinnerung abgeben.
Zum Ablauf:
Mag lässt sich eine 4-stellige Zahl nennen, die allerdings größer 2000 sein sollte. Es genügt also, um eine größere 4-stellige Zahl zu bitten.
Diese schreibt Mag über das noch leere Quadrat.
Anschließend trägt er in alle Zellen Zahlen ein, bis das Quadrat fertig ist und er die Erklärung abgibt:
“Das Quadrat ist ein magisches, denn alle Reihen haben die gleiche Summe, die der Vorgabe entsprechen. Dabei ist keine Zahl doppelt.”
Die Jury wird nach Prüfung diese Aussage bestätigen.
Dazu ein paar kurze Bemerkungen:
Die Vorgabe sollte größer 2000 sein?
Geht man von einer Schlüsselzahl 9 aus, so muss von der Zahl in Zelle 25 die Schlüsselzahl 25-mal abgezogen werden, um zur Zelle 1 zu gelangen und in dieser noch eine positive Zahl verbleibt.
Damit muss die Zahl in Zelle 25 eine Zahl von mindestens 25*9 = 225 enthalten.
Die magische Summe ist das 7-fache der Zahl in Zelle 25. Das wäre 225*7 = 1575,
auf Tausender aufgerundet ist das 2000.
Bei einer Schlüsselzahl 7 ist das genau 1225 und aufgerundet ebenfalls 2000.
In der Praxis rechnet man, 9 aufgerundet = 10*175, die magische Summe des Grundquadrates, ergibt 1750, aufgerundet 2000.
Die Zahl für Zelle 25, die sich in der gewünschten Stelle befindet, erhält man durch Division der Summenvorgabe durch die Ordnungszahl.
Das ist bei der kleinstmöglichen Vorgabe von 2001 = 2001/7 = 285, Rest 6.
und bei einer maximal möglichen Vorgabe von 9999 = 9999/7 = 1428, Rest 3.
Bei einer so großen Zahl für Zelle 25 sollte bedacht werden, dass bei Verwendung der Schlüsselzahl 9, die kleinste Zahl 1428-24*9 = 1212 würde und die größte 1428+24*9 = 1644, was nicht gerade günstig wirkt.
In diesen Fällen sollte eine größere Schlüsselzahl gewählt bzw. berechnet werden.
Da die Zahl in Zelle 1 nicht Null werden darf, wird die Schlüsselzahl so groß gewählt, dass das 25-fache der Schlüsselzahl von der Zahl in Zelle 25 abgezogen werden kann. Die Schlüsselzahl muss gleich oder kleiner sein als der Quotient aus Zahl in Zelle 25 dividiert durch 25, Da 25 auch 100/4 ist werden einfach die Hunderter mit 4 multipliziert. Das ist bei der im Beispiel errechneten Zahl 1428 = 1428*4/100 = 14*4 = 56. Als Schlüsselzahl könnte 49, das ist auch 50-1, gewählt werden. Die mit dieser Schlüsselzahl berechneten Zahlen hätten dann die Größe von 252 bis 2604, was einer breiten Streuung entspricht.
Ein Vorteil, den eine größere Schlüsselzahl mit sich bringt, ist, dass das Publikum die Zahlenbildung nur schwer erkennen kann.
Nach der Festlegung der Schlüsselzahl kann dann, ausgehend von der Zahl in Zelle 25, die auf- und absteigenden Zahlen nacheinander berechnet und nach den Springerregeln eingesetzt werden.
Die Zahlen eines Blockes müssen zusätzlich um den Rest erhöht werden.
6.6.4. Mehrfach-Vorgaben * *
Auch die Mehrfach-Vorgaben können aus den bisherigen Ausführungen abgeleitet werden.
Trotzdem wird Mag, wegen der vielfältigen Regeln die dabei zur Anwendung kommen, ausreichende Beschreibungen mit einem Beispiel erläutern.
Wegen der Schwierigkeiten, die insbesondere in den etwas komplizierten Berechnungen bestehen, wurden diesen Rechenexperimenten zwei Sterne zuerkannt.
Der Ablauf
Als Beispiel hat Mag eine 3-fach-Vorgabe gewählt, wobei die magische Summe und 2 Zellenzahlen vorgegeben werden.
Mag bittet einen Zuschauer um Nennung einer mittleren 4-stelligen Zahl, die er über das noch leere Quadrat der 7. Ordnung schreibt. (Im Beispiel 4371)
Danach bittet er um eine 3-stellige Zahl kleiner 200, die er in eine Zelle einsetzt.
(Im Beispiel 175)
Ein 3. Zuschauer wird um eine 2-stellige Zahl gebeten, die er ebenfalls in eine Zelle des Quadrates einträgt. (Im Beispiel 64)
Diese Anfangssituation zeigt das Quadrat 1)
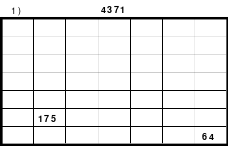
Im Anschluss trägt Mag in die noch leeren Zellen Zahlen ein, bis alle Zellen eine enthalten. Das Endergebnis ist das Quadrat 2)
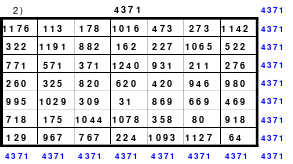
Das fertige Quadrat ist magisch. (und auch pandiagonal)
Die Summen aller Zeilen. Spalten und Diagonalen, auch der gebrochenen, entsprechen der vorgegebenen magischen Summe von 4351.
Die Zahlen sind gut gestreut. In den einzelnen Hunderter Zahlenreihen sind jeweils mindestens 2 vorhanden.
Die Lösung
Grundlage ist das Heptaquadrat, bei den Zeilen und Spalten so versetzt wurden, dass die mittlere Zelle 25 in der Mitte eingeordnet ist. Das ist nicht zwingend, jedoch vorteilhaft bei der Bestimmung der anderen Zellen und sollte auch nicht verändert werden, z. B. durch Vorgabe der Zelle mit der begonnen werden soll.
Die Zelle 1 befindet sich unter der Zelle 25 und ist die 1. im 1. Block. Die 1. Zahl im nächsten, den 2. Block, ist die 8. Die Zelle 8 befindet sich 2 Zellen nach links und 1 nach unten. Dieser Sprung ist ein Linkssprung, mit dem auch die anderen 1. Zellen in den Blöcken gefunden werden. So findet man die Zelle 15, die 1. Zelle des 3. Blockes, durch einen Linkssprung von der Zelle 8 aus. Mit weiteren Linkssprüngen gelangt man zu den 1. Zellen der weiteren Blöcke, das sind die Zellen 22, 29, 35 und 43. Diese werden aber nicht für den Einsatz von Vorgaben genutzt. Die Zelle 22 gehört zum 4. Block mit der Zelle 25, die frei bleiben muss, da diese aus der Summenvorgabe berechnet wird. Die anderen größeren Zellenzahlen sind die zweiten Duozahlen der Zellen 1, 8 und 15 und dürfen deshalb auch nicht mit einer Vorgabe belastet werden. Die zweiten Duozahlen sind leicht zu finden. Sie befinden sich symmetrisch zur mittleren, der Zelle 25. (Siehe Zellen mit gleicher Schattierung)
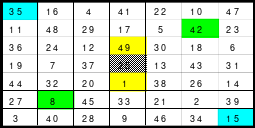
Mit diesen Kenntnissen ausgerüstet, kann die Berechnung aller übrigen Zahlen erfolgen.
Zuvor noch eine Erklärung. Die Zelle 1 sollte nicht mit einer Vorgabe belastet werden. Sie wird auf 0 gesetzt. Das hat den Vorteil, dass die Zahl in Zelle 49 ohne Abzug das Doppelte der Zahl in Zelle 25 wird. In die Zelle 1 wird der Rest eingesetzt und auch eine Reduzierung der Zahl in Zelle 25, um mit dieser besser rechnen zu können. Auf letzteres kann verzichtet werden, aber auch nur, wenn ein Rest entsteht, denn sonst würde eine Null in Zelle 1 stehen.
Was bei den Manipulationen für Zelle 1 zu beachten ist, wird im weiteren Text beschrieben.
Als erstes muss die Zahl für Zelle 25 berechnet werden. Das ist 4371/7= 624, Rest 3. In die Zelle 25 wird jedoch nur 620 eingesetzt. Damit sollen die folgenden Berechnungen etwas erleichtert werden.
In die Zelle 1 wird das 7-fache der abgezogenen 4, das ist 4*7=28, + Rest 3 = 31 geschrieben. Da alle Zahlen aus der Zahl in Zelle 25 abgeleitet werden, werden auch alle Zahlen um 4 reduziert. Das bedeutet, dass die Summen aller Reihen um 7*4 = 28 kleiner werden als die vorgegebene magische Summe. Um diese Reduzierung auszugleichen wird das 7-fache der Reduzierung, das ist 7*4=28, mit in die Zelle 1 eingesetzt.
Ist die letzte Ziffer der mittleren Zahl eine 0 und auch kein Rest vorhanden, was sehr unwahrscheinlich ist, muss eben 10 von dieser abgezogen werden und in die Zelle 1 wird 7*10=70 eingesetzt.
Es folgt die Berechnung der Zahl für Zelle 49. Alle Duosummen sind 620*2=1240 groß, auch die für das Duopaar 1/49. Da die Zelle 1 mit 0 belegt wurde, muss in die Zelle 49 die ungekürzte Duosumme mit 1240 eingetragen werden.
Als letztes werden die zweiten Duozahlen der Vorgaben berechnet. Das ist stets die Duosumme abzüglich der Vorgaben, somit 1240-175 = 1065 und 1240-64 = 1176.
Den erreichten Zwischenstand zeigt das Quadrat 3.
Mag hat als Schlüsselzahl 49 ermittelt. (Näheres in der Nachbetrachtung)
Nach erfolgter Überprüfung mit dem Ergebnis, dass die Differenzen zwischen den Vorgaben 175 und 64, sowie der berechneten Zahl 31 in Zelle 1, nicht durch die Schlüsselzahl 49 teilbar sind, können zum Abschluss die übrigen Zahlen berechnet und in die noch leeren Zellen eingesetzt werden.
Die kleinen Zahlen 31, 64 und 175 sind erste Zahlen ihrer Blöcke. Die weiteren Zahlen werden als aufsteigende Zahlenreihe mit +49 von Zahl zu Zahl berechnet.
(49 ist auch 50-1.)
Die großen Zahlen 1176, 1065 und 1240 sind die letzten Zahlen in ihren Blöcken. Deshalb werden hier die Zahlen absteigend mit -49 von Zahl zu Zahl gebildet.
Das so fertig gestellte Quadrat ist das am Anfang gezeigte Quadrat 2.
Eine Nachbetrachtung
Die maximal möglichen Vorgaben können nach der Formel
x = (O+1) /2+1
berechnet werden. Das sind beim 7er Quadrat x = (7-1) /2+1 = 4 und beim 5er Quadrat x = (5-1) /2+1 = 3. Das ergibt sich aus der Tatsache, dass für jede Zellenzahl als Duozahl eine Zahl als Partnerzahl berechnet werden muss, die
ebenfalls einem Block angehört. Somit bindet jede Zahlenvorgabe 2 Blöcke. Lediglich der mittlere Block benötigt keine Duopartnerzahl.
Die magische Summe kann nur vorgegeben werden, wenn die mittlere Zelle keine Vorgabe enthält und umgekehrt.
Günstiger ist es, die Anzahl der Vorgaben auf 1 weniger zu begrenzen, beim 7er Quadrat bleiben dann noch 3 Vorgaben. Dadurch kann die Zelle 1 frei bleiben und für die Aufnahme des Restes und anderer Manipulationswerte genutzt werden.
Auf die Vorgabe einer Zelle, in die eine Vorgabe einzugeben ist, sollte verzichtet werden, da eine solche nur für eine der Zellenzahlen möglich ist und die Übersichtlichkeit, und damit eine zügige Abarbeitung, nennenswert einschränken würde.
Für die Berechnung der Schlüsselzahl kann nur schwer eine genaue Lösung gefunden werden. Ein Überdecken der einzelnen Zahlenreihen ist immer möglich. Um sie zu vermindern sollte eine Zahl eingesetzt werden, die gleich oder kleiner 1/25-tel der kleinsten berechneten Duozahlen ist. Diese befindet sich im oberen Zahlenbereich des Quadrates und von ihr kann deshalb auch 1/25-tel abgezogen werden, ohne dass negative Zahlen entstehen.
Da die Betrachtungen zu den Begrenzungen der Vorgaben mit der Schlüsselzahl 9 erfolgten, kann diese natürlich auch eingesetzt werden. Allerdings ist dann die Streuung der Zahlen nicht optimal.
Das Quadrat 4) wurde mit der Schlüsselzahl 9 berechnet. Es ist nur bedingt vorzeigbar. Es fehlen 3-, 4-, 7-, 8- und 9-hunderter Zahlen. Auch erkennen die Zuschauer das ständige Zu- oder Abrechnen von 9 leichter als bei einer größeren Schlüsselzahl.
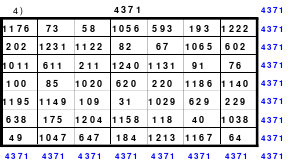
Mag berechnete aus der Zahl in Zelle 49 mit 12,4*4=49 eine mögliche Schlüsselzahl. Mit dieser berechnete er die Zahlen im Quadrat 2, das anfangs als fertiges Quadrat gezeigt wurde. Doppelte Zahlen konnten nicht auftreten, da die Differenzen zwischen den Zahlen in den Zellen 1, 8 und 15 nicht durch 49 teilbar sind. Dies Differenzen sind 175-31=144, 175-64=111 und 64-31=33.
Bei der Schlüsselzahl 9 war die Differenz 144 durch 9 teilbar, was an der Quersumme von 9 leicht erkannt wird. Da die Differenz 144 jedoch größer 7*9 = 63 ist, können doppelte Zahlen ausgeschlossen werden.
6.6.5. Einfach Clever * * (ein Experiment der “Hohe Schule”)
Eine Vorbemerkung
Die Routine zu “Einfach Clever” hatte Mag als erstes für ein Quadrat der 7. Ordnung erarbeitet und später bei den Quadraten der 4. und 5. Ordnung angewendet. Deshalb sind die folgenden Ausführungen sehr umfassend.
Beim 5er Quadrat war eine gekürzte Beschreibung mit Bezugnahme auf das 7er Quadrat nicht sinnvoll, da die Abhandlungen zu den 7er Quadraten erst später erfolgen.
Mag hat auf eine Überarbeitung der Beschreibungen zum 7er Quadrat mit Bezugnahme auf das 5er aus Zeitgründen verzichtet.
Er bittet um Verständnis, wenn vieles, dass aus den Erläuterungen zum 5er Quadrat bereits bekannt ist, wiederholt wird.
Denken Sie einfach daran, dass die Wiederholung die Mutter der Weisheit ist.
Einfach Clever mit einem Quadrat der 7. Ordnung
In der hohen Schule des Hexen 1x1 werden die zu bildenden Quadrate durch zeilenweise Eintragung der Zahlen erstellt. Das ist nicht so ohne weiteres machbar, denn das Erlernen der Zahlenfolge in einem Quadrat der 7. Ordnung ist kaum zu schaffen, zumal eine derartige Vorführung nur selten möglich ist. Es galt folglich Lösungen zu finden, die diesen Weg nicht erforderlich machen, eine Lösung die man sich kurzfristig ins Gedächtnis rufen kann und die auf Logik aufbaut.
Um eine einfache, leicht zu realisierende Lösung zu finden, hat Mag die Variante “Einfach Clever” gestaltet. Sie ist einfach und ohne Schwierigkeiten machbar. Sie hat allerdings einen kleinen Schönheitsfehler. Es kann dabei zu doppelten Zahlen kommen, was normalerweise nicht sein soll. Deshalb ist diese Variante auch mehr für Laien und weniger für den Profi geeignet.
Allerdings ist die Möglichkeit doppelter Zahlen sehr gering. Die Wahrscheinlichkeit kann bei 2-stelligen Vorgaben mit rd. 1 zu 20 und bei 3-stelligen Vorgaben mit nur noch 1 zu 100 eingeschätzt werden. Maximal können nur 6 Zahlen doppelt sein.
Nach Fertigstellung des Quadrates sollte deshalb die Aussage: ”... und keine Zahl ist doppelt” unterlassen werden.
Sollte ein Zuschauer eventuell auf doppelte Zahlen aufmerksam machen, so erklären Sie einfach, dass dies durch die Vorgabe, die Sie ja nicht gemacht haben, begründet ist und übrigens das Quadrat 49 Zellen hat und nur 90 2-stellige Zahlen verfügbar sind. Bei diesem Gedränge können doppelte Zahlen nicht ganz ausgeschlossen werden. Deshalb mussten Sie z. T. auch auf 3-stellige Zahlen ausweichen.
Eine Zahlenvorgabe
Auf der Tafel ist ein 7*7 = 49-zelliges Quadrat aufgezeichnet.
.Mag bittet einen Zuschauer um Nennung einer 2-stellige Zahl: Dieser nennt die Zahl 73, die Mag in die erste Zelle des Quadrates einschreibt. Sofort schreibt er über das Quadrat die Zahl 472. (linke Quadrate)
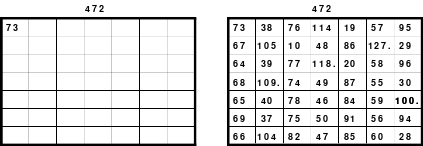
Anschließend füllt er zeilenweise alle Zellen des Quadrates mit Zahlen aus, wozu er keine 5 Minuten benötigte. Das fertige Quadrat ist magisch, mit der magischen Summe von 472, die er vorher über das Quadrat geschrieben hat. (rechtes Quadrat)
Die Lösung
Eine kurze Abhandlung was Mag wirklich macht:
Nach der Eintragung der Vorgabe 73 in die Zelle 1, addiert Mag zur Vorgabe die Primärzahl 399, das ist auch 400-1 und erhält so die magische Summe von 472, die er über das Quadrat schreibt. Die Primärzahl muss sich Mag merken, sie kann aber auch leicht berechnet werden. Anschließend schreibt er in die folgenden 6 Zellen die Zahlen 38, 76, 114, 19, 57 und 95. Diese Zahlen muss Mag sich nicht merken, denn sie sind ganz leicht zu berechnen. Diese 6 Zahlen bezeichnet Mag als Flexzahlen. (Diese sind flexibel)
(Sie ergeben sich aus 2*9+2*10=38, oder 4*9+4*10=76 bis zur letzten Zahl in Zeile 1 mit 5*9+5*10=95 - warum, wird in der detaillierten Beschreibung erläutert.)
Damit ist die 1. Zeile fertig. Die Summe aller 7 Zahlen ergibt die magische Summe von 472, die Mag vorher über das Quadrat geschrieben hat.
Nun folgt die 2. Zeile, beginnend mit der 1. Zelle in dieser. Dazu geht Mag 1 Zelle nach oben und 2 nach rechts. Dort ist die Zahl 76, von der er 9 abzieht und das Ergebnis 67 in die 1. Zelle der 2. Zeile einschreibt. Dann folgt die nächste Zelle. Auch hier 1 nach oben und 2 nach rechts und von der 114 wird 9 abgezogen was 105 ergibt, die er einsetzt. (9 ist die festgelegte Schlüsselzahl). So werden die Zahlen für alle weiteren Zellen berechnet und eingetragen.
Lediglich von der jeweils 1. Zahl im Block darf keine weitere 9 abgezogen werden, Hier muss 54 (6*9) zugezählt werden. Das ist bei der vorletzten Zelle in Zeile 2 der Fall. 1 nach oben, 2 nach rechts und man kommt auf die Zelle mit der Vorgabe und das ist ja die 1. Zahl im 1.Block. Von dieser darf nicht mehr die 9 abgezogen werden, sondern diese muss um 54 erhöht werden und die Zahl für die vorletzte Zelle in der 2. Zeile ist 73+54=127. Dies trifft auch auf die anderen 1. Zahlen der Blöcke zu. Diese erkennt Mag an der 0 als letzte Ziffer. Das ist z. B. in der 3. Zelle der 2. Zeile mit der Zahl 10 der Fall, weshalb in die 1. Zelle der 3. Zeile nicht 10-9=1, sondern 10+54=64 einzusetzen ist.
Das fertige Quadrat ist pandiagonal mit der magischen Summe von 472 in jeder Spalte, Zeile und Diagonalen.
Auf weitere, aber geringfügige Probleme wird später eingegangen.
Mag hat diese Handlungen der detaillierten Beschreibung vorangestellt, um zu zeigen, dass es sich um eine wirklich sehr leichte Lösung handelt. die ohne weiteres beherrscht werden kann und damit für Anfänger bestens geeignet ist.
Doch nun zu den Details der Lösung
Die Grundlage für dieses Experiment sind einmal das Heptaquadrat, ein Quadrat der 7. Ordnung und zum anderen ein alternatives Heptaquadrat. Das alternative Quadrat entstand durch wenden des Haptaquadrates um die waagerechte Achse und versetzen der unterste Zeile nach oben.
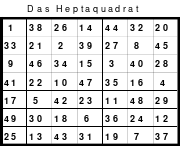
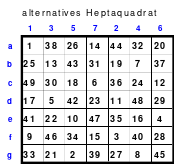
Das alternative Heptaquadrat ist ebenfalls ein Springerquadrat, wobei die Sprünge innerhalb eines Blockes 2 nach rechts und 1 nach oben sind. Der Übergang von Block zu Block ist 2 nach oben. Daraus ergibt sich die Situation, dass die vorangegangene Zahl, die ja um 1 größer ist, in der Regel durch 1 Zelle nach oben und 2 Zellen nach rechts zu finden ist.
Damit ist die Berechnung der 2. bis 7. Zeile erklärt.
Die wichtigen Flexzahlen und die Primärzahl sind noch zu erklären.
Dazu ist die grün schattierte Tabelle zu beachten.
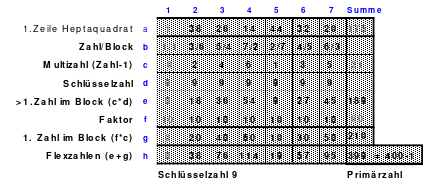
Die erste Zeile der Tabelle (a) enthält die Zellenzahlen der 1. Zeile des Heptaquadrates. Analysiert man diese Zahlen, so ist die Zahl 38 die 3. Zahl des 6 Blockes, die 26 die 5. des 4. Blockes usw. Diese Angaben für alle 6 Zahlen (38, 26, 134, 44, 32 und 20 sind in Zeile 2 (b) dargestellt. Die 3. Zahl im Block ist um 2 größer als die 1. Zahl des Blockes. Die 5. um 4 größer usw. Diese Zahlen nennt Mag Multizahlen (c), denn sie werden mit der Schlüsselzahl (d), im Beispiel die 9, multipliziert und man erhält so die Werte die dem Wert der 1. Zahl im Block zugeschlagen werden müssen. Diese Werte sind in der 5. Zeile (e) zu finden. Nun müssen noch die Werte für die 1. Zahlen der Blöcke gefunden, bzw. bestimmt werden. Hier geht Mag den einfachsten Weg, indem er die zugehörigen Multizahlen mit den Faktor 10 multipliziert. Diese Werte sind in Zeile 7 (g) enthalten. Durch die Multiplikation mit 10 haben alle Zahlen als letzte Ziffer eine Null und können dadurch wie vorn beschrieben leicht erkannt werden. Werden die Zahlen der 5. und 7. Zeile addiert, so erhält man die Flexzahlen (h), die in das zu berechnende Quadrat übernommen werden.
Die einfache Berechnung der Flexzahlen kann schnell erfolgen, weshalb diese nicht gemerkt werden müssen. Allerdings müssen die Multizahlen erlernt sein, was ziemlich leicht ist. Denn zuerst kommen die geraden Zahlen 2, 4 und 6 in aufsteigender Reihe und anschließend ebenfalls aufsteigend die ungeraden Zahlen 1, 3 und 5.
Die sehr kleine Pause die bei der jeweiligen Berechnung entsteht ist gewollt, weil sie so dem Zeitaufwand zu den Berechnungen der übrigen Zellenzahlen entspricht.
Die Addition der 6 Flexzahlen ergibt die Summe von 399, was auch 400-1 ist. Diese Zahl ist die Primärzahl mit deren Hilfe die magische Summe berechnet wird.
Sollten in der Berechnung noch Unklarheiten bestehen, empfiehlt Mag den Abschnitt “Eine kurze Abhandlung was Mag wirklich macht” nochmals auszuwerten.
Leider ist diese einfache Lösung nicht ganz ohne Probleme.
Eines ist die Möglichkeit, dass doppelte Zahlen vorkommen können, was nur durch eine ungünstige Vorgabe entstehen kann und eine Verhinderung fast unmöglich ist, da zur Prüfung umfangreiche Berechnungen notwendig sind.
Schnell geprüft werden kann aber, ob die Vorgabe gleich einer Flexzahl ist, was zu doppelten Zahlen bereits in der 1. Zeile führen würde. Das betrifft allerdings nur Vorgaben mit den Endziffern 4 bis 9 Hier wird einfach die letzte Ziffer der Vorgabe von 10 abgezogen und der ermittelte Wert wie eine Multizahl zur Berechnung einer gedachten Flexzahl genutzt. Ist dieser errechnete Wert gleich der Vorgabe, so ist die Vorgabe gleich einer der 6 Flexzahlen, das heißt, eine der von Mag eingesetzten Flexzahl entspricht der Vorgabe.
Als Beispiel die Prüfung der Vorgabe 76: 10-6=4 >> 4*9+4*10=76. Damit ist die errechnete Flexzahl gleich der Vorgabe und entspricht der 2. Flexzahl in der Tabelle.
In diesem Fall sollte auf die Schlüsselzahl 7 ausgewichen werden.
Dazu finden Sie die erforderlichen Parameter in der nachfolgenden gekürzten Tabelle.
Hier sind die Flexzahlen gleich 44, 78, 112, 27, 61 und 95.
Die Primärzahl ist 417 = 400+17.
Die Differenzen zwischen den Zahlen innerhalb eines Blockes ist 7.
Bei Erreichen der Zahlen mit Endziffer 0 wird nicht 7 abgezogen, sondern 6*7=42 zugeschlagen. (Dieser Wert ist bei der Schlüsselzahl 9 = 6*9=54.)
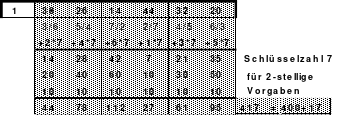
Abweichend zur Tabelle zur Schlüsselzahl 9 ist die zusätzliche Erhöhung der Zahlen für die ersten Zellen mit 10. Dadurch konnte die Primärzahl mit 417 erreicht werden, die sonst 357 betragen hätte.
Ein weiteres Problem ist die Erhöhung bei Erreichung der 1. Zahl des Blockes, was durch eine Null erkennbar ist. Hier wird nicht 9 oder 7 abgezogen, sondern 54 oder 42 zugezählt. Es kann passieren, dass im 1. Block, der mit der Vorgabe beginnt, ein Zwischenergebnis mit einer Endziffer Null vorkommt, der natürlich nicht um 54 bzw. 42 erhöht werden darf. Das ist bei der Schlüsselzahl 9 u. a. bei einer Vorgabe mit den Endziffern 2, 3, 4, 5 und 6 möglich. Ein Beispiel ist im anfangs berechneten Quadrat mit der Vorgabe von 73 vorhanden. Hier befindet sich in der letzten Zelle der 5. Zeile die Zahl 100. Um Irrtümer auszuschließen hat Mag die Zahlen des 1. Blockes, die mit der Vorgabe beginnen, durch einen Punkt kenntlich gemacht. Das kann auch durch eine weniger auffallende Kennzeichnung erfolgen, welche, bleibt Ihnen überlassen.
Eine weitere Reduzierung möglicher Doppelzahlen auf etwa 1% ist die Vergrößerung der 1. Zahlen der Blöcke, z. B. durch Multiplikation der Multizahlen mit den Faktor 100.
Nachfolgend sind dazu die Tabellen mit den Parametern für die Schlüsselzahlen 9 und 7 abgebildet. Auch hier sind bei der Schlüsselzahl 7 die 1. Zahlen der Blöcke zusätzlich um 10 erhöht.
Zur Anwendung dieser Flexzahlen und Primärzahlen ist keine weitere Erklärung notwendig.
Als Beispiel hat Mag ein Quadrat der 7.Ordnung nach der letzten Tabelle mit einer 3-stelligen Vorgabe von 367 gebildet. Die Schlüsselzahl ist 7. Die magische Summe wurde mit 367+2300+7= 2674 ermittelt.
Das Quadrat ist magisch mit der magischen Summe 2674 und auch pandiagonal.
Keine Zahl ist wegen der viel geringeren Wahrscheinlichkeit doppelt.
Vorgabe der magischen Summe *
Nach dieser Methode ist auch die Erstellung eines magischen Quadrates bei Vorgabe der magischen Summe möglich. In diesem Fall erfolgt die Berechnung im umgekehrten Sinn, d. h. von der Vorgabe wird die Primärzahl abgezogen und man erhält die Zahl für die Zelle 1. Die weiteren Berechnungen erfolgen dann wie bisher bei Vorgabe einer Zahl für Zelle 1 beschrieben.
Allerdings ist die Bildung eines magischen Quadrates bei Vorgabe der magischen Summe schwerer zu lösen als dies bei der Vorgabe einer Zahl für Zelle 1 ist. Mag wird anhand eines Beispiels das zusätzliche Problem sichtbar machen.
Er hat aber auch Wege gefunden, um dieses Problem zu beherrschen. Diese Lösungen sind jedoch schwerer zu realisieren, weshalb Mag den Rat gibt, auf die Lösung entsprechend dem “Kleinen Hexen 1x1”, oder dem “Königsquadrat“
auszuweichen. Das gilt besonders für 4-stellige Vorgaben die mit einer Schlüsselzahl von nur 9 oder 7 nicht erstellt werden sollten, da die Streuung der Zahlen völlig unbefriedigend ist.
3-stellige Vorgaben sollten möglichst auf die Schlüsselzahl 9 beschränkt werden.
Nun ein Beispiel.
3-stellige Vorgaben
Mag hat um eine 3-stellige Vorgabe aus dem oberen Bereich, größer 500, gebeten.
(Aus dem oberen Bereich deshalb, da nach Abzug der Primärzahl von 399 eine positive Zahl für Zelle 1 übrigbleiben muss!)
Nachfolgend ein Beispiel mit der Vorgabe der 3-stelligen magischen Summe von 978.
Die Berechnung erfolgt mit der Schlüsselzahl 9 bei der die Primärzahl 399 ist.
Mag hat von 978 erst 400 abgezogen und dann um 1 erhöht, das ist eine Reduzierung um 399 was der Primärzahl entspricht und damit 978-400=578+1=579 erhalten, die in die Zelle 1 eingesetzt wurde.
Alle weiteren Schritte erfolgen in der bekannten Weise.
Auch hier wurden alle Zahlen des 1. Blockes mit einem Punkt versehen.
Das entstandene Quadrat ist magisch mit der magischen Summe von 978, was der Vorgabe entspricht. Es ist auch pandiagonal.
Allerdings gibt es hier neben den bereits genannten Problemen ein weiteres, das mit der Vorgabe von 978 kenntlich gemacht wird.
Es ist auffallend, dass neben den vorwiegend nur 2-stelligen Zahlen 3-stellige Zahlen, größer 500 im Quadrat vorhanden sind, was durch die hohe Vorgabe bedingt ist.
Um diese Zahlen zu reduzieren, müssen die übrigen Zahlen logischerweise vergrößert werden. Das ist möglich durch Erhöhung des Faktors der ja durch Multiplikation mit der Multizahl zu einer größeren ersten Zahl im Block und damit auch aller anderen Zahlen des Blockes führt.
Die Erhöhung erfolgt dabei in 10er Schritten, jedoch nur bei den Multizahlen 2 bis 6. also nicht für die Multizahl 1. Der Grund ist, dass die Multizahlen von 2 bis 6 in ihrer Summe 20 ergeben. Wird 10 mit 20 multipliziert, erhält man 200 und damit eine Zahl, mit der nicht nur einfacher gerechnet werden kann, sondern auch eine Null als wichtiges Erkennungsmerkmal als Endziffer hat.
Nach diesen Regeln wird als Beispiel eine Neuberechnung mit der Vorgabe 978 erstellt.
Geht man davon aus, dass eine Vorgabe größer 500 gefordert wird, reicht die bisherige Berechnung der Flexzahlen aus, um Vorgaben bis 700 zu berechnen. Wird
die Vorgabe jedoch größer, müssen die Flexzahlen entsprechend erhöht werden. Die nächste Stufe wäre dann größer 700 und die übernächste größer 900.
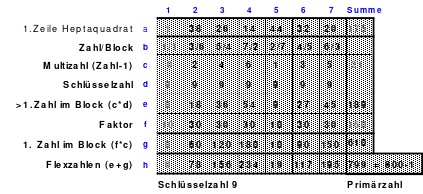
Die Vorgabe mit 978 ist rd. um 400 größer als 500, der geforderten Mindestgröße. (Es wird einfacher nur mit den Hunderten gerechnet!)
4/2 = 2, folglich sind die Faktoren (außer für die Multizahl 1) um 2*10=20 auf 30 zu erhöhen.
Die Veränderungen der Flexzahlen und der Primärzahl sind in der Tabelle ersichtlich. Das mit diesen Werten neu berechnete Quadrat sieht viel gefälliger aus, denn die Differenzen zwischen den Zahlen sind jetzt ausgeglichener. Wie nach der Regel zu erwarten war, sind keine doppelten Zahlen vorhanden.
In der gleichen Art und Weise können die Quadrate mit der Schlüsselzahl 7 erstellt werden. Beachten Sie dazu die Tabelle.
Einige Änderungen sind vorhanden. So wurde wie bei Schlüsselzahl 9 nicht nur die Erhöhung des Faktors für Multizahl 1 weggelassen, sondern auch der Zuschlag von 10. Dadurch konnte eine weitere Verbesserung der Primärzahl erreicht werden, was für die Berechnung günstiger ist. So wurde die Primärzahl 607 und nicht 617 groß.
Bei einem Zusatzfaktor von 0 in allen Spalten wird die Primärzahl 417 groß, das ist eine um ~200 kleinere Zahl.
Auch hier eine Quadratbildung mit der Vorgabe von 792 als Beispiel.
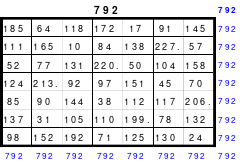
Auch dieses Quadrat hat keine doppelten Zahlen.
4-stellige Vorgaben der magischen Summe
Auch wenn Mag die Bildung magischer Quadrate, insbesondere mit 4-stelligen Vorgaben der magischen Summe, nicht als sinnvoll erklärt hat, so geht er jetzt darauf ein umso auf die schwierigere Lösung als bisher beschrieben aufmerksam machen zu machen, was besonders für Anfänger gilt.
Grundsätzlich scheidet eine Schlüsselzahl von 9 aus. Das würde zu Zahlen führen die nur kleine Differenzen aufweisen und die 7 Zahlen jedes Blockes, die auch Tausender Zahlen sein können, würden mit einer Differenz von nur 9 annähernd gleich sein. Um eine günstige Verteilung der Zahlen zu erreichen ist eine größere Schlüsselzahl notwendig. Mag empfiehlt eine Schlüsselzahl von 109.
Es soll ein Quadrat mit der magischen Summe von 9013 gebildet werden.
In der nachfolgenden Tabelle ist die Bildung der dafür benötigten Werte aufgezeigt. Sie gleicht den Tabellen für 3-stellige Vorgaben, wobei die Faktoren 100 groß sind. Auch die Zahlen in der 4. Zeile sind durch den Einsatz der Schlüsselzahl 109 größer.
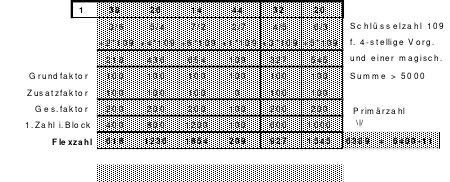
Bei der Grundvariante mit einem Zusatzfaktor 0, würde die Primärzahl 4389 groß sein. Das bedeutet, dass um eine Vorgabe >5000 gebeten werden muss. Mit der Grundvariante können Vorgaben bis 7000 berechnet werden. Für größere Vorgaben, wie im Beispiel müssen die Faktoren für die Multizahlen um weitere 100 auf 200 erhöht werden.
Mit den berechneten Flexzahlen und der Primärzahl kann das Quadrat gebildet werden.
Zur Erinnerung:
Die Zahl für Zelle 1 wurde berechnet mit 9013-6400+11=2624.
Die Zahlen für die anderen Zellen wurden berechnet, indem von der Zahl in 1 nach oben und 2 nach rechts 109 abgezogen wurde.
Ausnahmen sind Zahlen, deren letzte Ziffer eine 0 ist und kein Kennzeichen (.) hat. Hier musste 6*109=654 zugeschlagen werden.
Ebenfalls um 654 muss die Zahl aus Zelle 1 erhöht werden. Die Zelle in die dieser erhöhte Wert eingesetzt werden muss, ist 2 nach links und 1 nach unten.
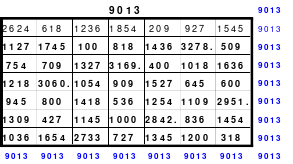
Das Quadrat ist magisch und pandiagonal mit der Vorgabe 9013 als magische Summe.
Die Zahlen sind breit gestreut. Es sind 19 Zahlen unter 1000, 23-mal 1000er, 4-mal 2000er und 3-mal 3000er.
Eine noch bessere Strukturierung kann erreicht werden, wenn die Zusatzfaktoren mit 50 festgelegt werden. Denn 50*20=1000. Mag wird aber nicht weiter darauf eingehen, da er dies als nicht notwendig betrachtet und die Berechnungen zusätzlich erschwert.
Auffallend sind die Zahlen mit 2 und sogar 4 Nullen als letzte Ziffern. In jeder Zeile ist eine davon vorhanden. Das kann, wenn gewünscht, geändert werden. Dazu ist die zu berechnende Zahl für die Zelle 1 um ein durch 6 teilbare Zahl zu kürzen und dafür die Flexzahl um 1/6 der Kürzung zu erhöhen. Vorteilhaft wäre die 30, um die die Zahl für Zelle 1 gekürzt wird und zum Ausgleich die Flexzahlen um 5 erhöht werden. Die erste Zeile würde dann der Abbildung entsprechen.
Alle Hunderten Zahlen würden eine 5 als letzte Ziffer haben. Das führt allerdings auch dazu, dass die ersten Zahlen der Blöcke, die um das 6-fache der Schlüsselzahl erhöht werden müssen, mit einer 5 als Kennzeichen enden.
Die Frage ist berechtigt, ob sich der zusätzliche Aufwand wirklich lohnt. Das muss jeder für sich entscheiden.
Bestimmung der Zelle mit der begonnen werden soll
Mag hat mehrfach betont, dass die erstellten Quadrate pandiagonal sind. Das bedeutet, dass die Zelle 1 an jeder Stelle des Quadrates eingeordnet werden kann. Das nutzt Mag dazu, dass er von den Zuschauern bestimmen lässt, mit welcher Zelle begonnen werden soll. Es ist egal welche Zelle bestimmt wird, für Mag ist es die Zelle 1, in die er die Vorgabe oder Differenz zur Vorgabe bei magischen Summen, einsetzt. Im Anschluss werden die Flexzahlen eingetragen. Wird der rechte Rand erreicht, geht es links weiter. Wichtig ist dabei, dass auch die Zelle 1 mit dem Kennzeichen (.) versehen wird. Auch eine Einrahmung als Bestätigung der Zelle 1 ist denkbar. Dann geht es weiter mit der 3. Zeile in die von links nach rechts die Zahlen eingesetzt werden. Bei der Ausfüllung der obersten Zeile wird auf den untersten Bezug genommen.
Das zuletzt gebildete Quadrat mit der Vorgabe der magischen Summe von 9013 würde dann wie folgt Gestalt annehmen, wenn der Zuschauer die 3. Zelle in der 2, Zeile als Anfang bestimmt. Mag Hat diese Zelle nochmals umrahmt.
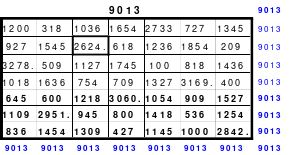
Mit diesem Quadrat schließt Mag seine Ausführungen zu “Cleveres für Anfänger” ab.
Eine Nachbetrachtung
Die letzten Ausführungen zu Quadraten mit 4-stelligen Vorgaben sind als eine erweiterte Betrachtung der Grundvariante zu bewerten. Sie dürften für Vorführungen in Programmen als Rechenkünstler ungeeignet sein.
Die mehrfachen und oft auch uneinheitlich vorgenommenen Änderungen, können zu einem Verlust der Übersicht führen.
Es wird auf die Ergänzungsvarianten 1 bis 4, die im 5er Quadrat “Einfach Clever” enthalten sind, verwiesen. Sie entstanden nach den Erläuterungen zum 7er Quadrat und sind deshalb nicht vollständig in dieser enthalten.
Dort wird beschrieben, wie gesichert wird, dass keine doppelten Zahlen auftreten, wie bei Wiederholungen zu verfahren ist und dass die Zuschauer bestimmen können, mit welcher Zelle zu beginnen ist, denn das alternative Heptaquadrat ist ein pandiagonales. (Letzteres wurde im 7er Quadrat beschrieben.)
In der weiteren Folge wird er das “Königsquadrat” vorgestellt, dass nicht nur eine höhere Qualität hat, sondern auch schwieriger in der Anwendung ist, weshalb es auch 2 Sterne erhalten hat.
6.6.6. Das 7er Königsquadrat * * (Ein Experiment der hohen Schule)
Im Abschnitt “Hexen 1x1 mit Quadraten der 5. Ordnung” hat Mag das Königsquadrat ausführlich beschrieben. Deshalb wird zum 7er Königsquadrat nur auf Nennenswerte eingegangen und auf Beispiele verzichtet.
Das 7er Königsquadrat hat Mag mit den Parametern des 5er Königsquadrates gebildet.
Diese sind:
Abstand zwischen den Zahlen innerhalb der Blöcke ist 3 Zellen nach rechts und 1 nach unten. Der Übergang von Block zu Block ist 1 nach rechts.
Das so entstandene Königsquadrat ist magisch und pandiagonal. Die magische Summe ist 175. Die mittlere Zelle ist die Zelle 25. Die magische Summe ist das 7-fache der mittleren Zahl 25.
Da das Königsquadrat ein pandiagonales ist kann auch die Zelle 25 als 1. der 1. Zeile eingeordnet werden. Das so entstandene rechte Quadrat wurde ebenfalls zwecks einer Analyse gesperrt dargestellt. Die Analyse dieses Quadrates ergab, dass dieses nach ähnlichen Regeln wie das 5er Königsquadrat aufgebaut ist.
Diese sind:
In der Zeile ist die folgende Zellenzahl um 8 größer. Außer bei Zellenzahlen, die durch 7 teilbar sind (7, 14, 21, 28,..... 42, 49). Hier ist die folgende Zellenzahl nur um 1 größer.
Die erste Zellenzahl der folgenden Zeile ist um 15 kleiner als die letzte Zellenzahl der vorhergehenden Zeile. Außer bei Zellenzahlen, die nach Abzug von 1 durch 7 teilbar sind (1, 8, 15, 22, ....43). Hier ist die erste Zahl der folgenden Zeile nur um 8 kleiner.
In allen Fällen gilt: Ist die errechnete Zellenzahl größer 49, so muss 49 abgezogen werden. Ist sie kleiner 1, so muss 49 zugezählt werden.
Gleichzeitig muss von der berechneten Zahl auch das 49-fache der Schlüsselzahl abgezogen oder zugerechnet werden.
Diese Regeln sind leicht zu merken und ermöglichen die Berechnung der jeweils folgenden Zellenzahl, egal wo begonnen wird.
Der Vergleich der Regeln des 5er mit dem 7er Königsquadrat zeigte, dass die nach den Regeln ermittelten Parameter mathematisch berechenbar sind und in empirischen Formeln dargestellt werden können. Das zeigt die folgende Tabelle.
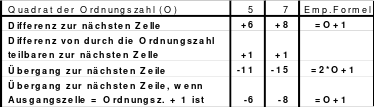
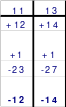
Auf diesen Erkenntnissen aufbauend können die Parameter auch für weitere Primzahlquadrate errechnet werden. Siehe dazu die Zahlen für das 11er und 13er Quadrat, die an die Tabelle in blauer Schrift angehängt wurden. Diese Zahlen wurden mittels der empirischen Formeln berechnet.
Interessant dürfte dabei das 11er Königsquadrate sein. Hier wird an den Zellenzahlen erkannt, ob die letzte Zellenzahl durch die Ordnungszahl teilbar ist. Diese Zahlen bestehen aus 2 gleichen Ziffern (11, 22, 33, ... 99, ausgenommen 110 und 121). Auch die um 1 größeren Zellenzahlen sind zu erkennen (12, 23, 34, usw.).
Zurück zum 7er Königsquadrat
Die Schlüsselzahlen für das 7er Quadrat müssen gleich oder kleiner sein als berechnet. Diese erfolgt durch Division der Vorgabe in Zelle 25 durch 25. Da 100/4 auch 25 ist, wird rationell die Vorgabe durch 100 geteilt (gedanklich das Komma 2 Stellen nach links gesetzt) und mit 4 multipliziert.
Bei Vorgabe der magischen Summe muss als erstes die Zahl für Zelle 25 durch Division der Vorgabe durch 7 berechnet werden.
Ist beabsichtigt, die Schlüsselzahl wie beim 5er Quadrat, mit 100 bis 300 +/- bis 3 festzulegen, müssen die Zahlenvorgaben größer 2500 sein und die Summenvorgaben größer 17500.
Selbstverständlich kann auch beim 7er Königsquadrat mit der Schlüsselzahl 3 gerechnet werden. Hier genügen Zahlenvorgaben >75 “Eine Zahl aus der Einhunderterreihe” und Summenvorgaben >525 “Eine 3-stellige Zahl aus dem oberen Bereich”.
Die Zelle 25 kann durch Versetzen von Zeilen und/oder Spalten an jede beliebige Stelle versetzt werden. Das ermöglicht, dass vom Publikum die Zelle genannt werden kann, mit der begonnen werden soll.
Damit dürfte das Wichtigste zum 7er Königsquadrat gesagt sein und weitere Erläuterungen sind nicht erforderlich.
Die Berechnungen zur Bildung eines Quadrates auf der Grundlage von Vorgaben wird analog der Beschreibungen zum 5er Königsquadrat abgearbeitet.
6.6.7. Das rationelle 7er Quadrat
Die in den Ausführungen zum Hexen 1x1 mit Quadraten der 5. Ordnung beschriebene rationelle Rechenmethode kann auch auf andere Primquadrate übertragen werden.
Damit rückt das 7er Heptaquadrat möglicherweise in den Bereich der für Vorführungen noch geeignete Quadrate, was aber nur eine Ausnahme sein darf.
Dabei sollte jedoch nur die Vorgabe der magischen Summe als 4-stellige Zahl aus dem oberen Bereich erfolgen. Auf eine Zahlenvorgabe ist wegen der etwas schwierigeren Berechnung der magischen Summe nach Möglichkeit zu verzichten. Allerdings entsteht bei Vorgabe der magischen Summe meist ein Rest, der der Startzelle in Zeile 1 zugeschlagen werden muss.
Auch sollte aus Orientierungsgründen auf die Vorgabe einer Anfangszelle verzichtet werden.
Voraussetzung ist, dass Sie sich mit den Beschreibungen im Abschnitt “Hexen 1x1” mit “Quadraten der 5. Ordnung” vertraut gemacht haben.
Zur Erinnerung nochmals die anzuwendenden Sprünge
Wie beim Pentaquadrat befinden sich die mittlere Zahl 25 in der Mitte des Quadrates und die 1 unterhalb von dieser. Die größte Zahl, hier die 49, befinde sich oberhalb der mittleren Zahl 25.
Auch werden die entsprechenden Zellen 42 (letzte Zelle im 6. Block) und 35 (letzte Zelle im 5. Blockes) durch Returnsprünge von Zelle 49 ausgefunden und die Zellen 8 (1. Zelle im 2. Block) und 15 (1.Zelle im 3. Block) mit Linkssprüngen von Zelle 1 aus.
Die so ermittelten Startzellen sind in der folgenden Abbildung klar zu erkennen.
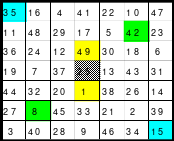
Die Bildung der DZ1 (Differenzzahl 1) erfolgt analog wie beim Pentaquadrat.
Die DZ2 wird dann DZ1/3,5 (3,5=Ordnungszahl/2), wobei rd. DZ1/10 (Streichung der letzten Ziffer) und dann *3 gerechnet werden kann. Das Ergebnis ist zwar 5 % größer als der genaue Wert, wird aber durch die Abrundungen ausgeglichen,
Die Schlüsselzahl ist DZ2/7 (7=Ordnungszahl) und ist auf eine leicht zu handhabende Zahl zu reduzieren.
Die Berechnung der Startzellen und auch die Zellen der einzelnen Blöcke werden analog der Berechnung des 5er Quadrat vorgenommen.
Dabei entsteht ebenfalls eine leicht zu merkende Einordnung. Alle Zellen, von denen aus den Zahlen in absteigender Folge berechnet werden, befinden sich oberhalb der Mittleren Zelle und die von denen aus der Berechnung aufsteigend erfolgt unterhalb.
Auch befinden sich die letzten zu berechnenden Startzahlen in der 1. bzw. letzten Zeile.
Alle Regeln aus dem 5er Quadrat gelten auch im 7er.
Dazu ein Beispiel
Links ist das Heptaquadrat, ein Primquadrat der 7. Ordnung, abgebildet. Die Spalten und Zeilen wurden so verschoben, dass die mittlere Zahl 25 in die Mitte des Quadrates zu liegen kam.
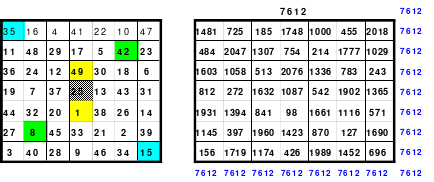
Das rechte Quadrat wurde durch folgende Berechnungen gebildet:
Mittels der SZ wurden die Zahlen für die restlichen Zellen wie im 5er Quadrat berechnet und eingesetzt.
Das fertige Quadrat ist magisch mit der vorgegebenen MS = 7612 und pandiagonal.
6.7. Quadrate der 8. Ordnung
6.7.1. Das Meisterquadrat
Eine Vorbemerkung
Das folgende Rechenexperiment hat Mag damals nicht so vorgeführt, sondern entsprechend der alternativen Variante, wobei er damals die Multimethode zur Berechnung des Quadrates nutzte. In die folgenden Erläuterungen sind seine späteren Erkenntnisse eingeflossen, wobei die Grundvariante erhalten blieb.
Nach weiteren Betrachtungen erkannte Mag, dass die alte Variante durchaus beachtet werden sollte, zumal sie keine Forderung nach einer geraden Vorgabezahl stellt.
Zum Meisterquadrat
Eigentlich hatte Mag nicht vor das Meisterquadrat im Hexeneinmaleins zu beschreiben. Es handelt sich dabei um ein Quadrat der 8. Ordnung, in das nach einer von den Gästen genannten Summe unterschiedliche Zahlen eingesetzt werden, deren Summen der vorgegebenen entsprechen. Es grenzt fast an eine Frechheit mit welchen Tricks Mag hier arbeitet. Das bedeutet allerdings nicht, dass das Rechnen ganz einfach ist.
In der Öffentlichkeit ist eine Vorführung kaum gegeben. Im kleinen Kreis ist es jedoch durchaus machbar, wenn daran ein Interesse besteht.
Die Idee wurde von Mag anlässlich einer Geburtstagfeier im kleinen Familienkreis geboren. Dabei kam sein Hobby ins Gespräch und die Bitte etwas zu zeigen. Nachdem er ein Quadrat der 3. Ordnung mit einer vorgegebenen Summe gebildet hatte, wurde er gefragt, ob er das auch mit richtig großen Quadraten machen könne. Mag war es gewohnt Vorführungen mit kleinen Quadraten zu gestalten. Er überlegte, mit welcher Ausrede er antworten sollte, als ihm die Idee einer Lösung in den Kopf schoss und er antwortete, dass er das natürlich kann und bat um ein Blatt Papier und Bleistift.
Nachdem er ein 8 mal 8 Felder großes Quadrat aufgezeichnet hatte, bat er um Nennung einer geraden 4-stelligen Zahl. Es wurde die Zahl 1694 genannt. Diese schrieb Mag über das Gesamtquadrat.
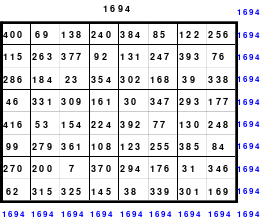
Anschließend füllte er die einzelnen Zellen der ersten Zeile mit Zahlen aus. Dann folgte die zweite Zeile, die dritte usw. bis das Quadrat nach ca. 10 Minuten fertig war.
Mag erklärte, dass das gebildete Quadrat ein Quadrat der 8. Ordnung ist und die Summen aller Reihen der vorgegebenen Summe von 1694 entsprechen. Damit ist das Quadrat ein magisches, wobei keine Zahl doppelt vorhanden ist.
Danach kontrollierten die Gäste einige Reihen und konnten sich davon überzeugen, dass die Summen der Reihen die der Vorgabe von 1694 haben, wozu diese natürlich einen Taschenrechner oder Smartphon benutzten.
Zweifler bescheinigten Mag, dass er tatsächlich ein Meister des magischen Quadrates ist, weshalb Mag diese Variante auch den Namen “Meisterquadrat” gab.
Wie hatte Mag das gemacht?
Da Mag die Zahlen eines 8er Basis-Quadrates nicht im Kopf hat, konnte er auch kein solches errechnen. Er griff zu einer List. Mag hat ganz einfach gedanklich 4 Topquadrate zu einem 8 mal 8 großen Quadrate zusammengefügt, wobei jedes eine magische Summe haben muss, die der halben Vorgabe entspricht. Natürlich konnten nicht 4 gleiche Quadrate gebildet werden. Der Trick war, dass nur das erste, links oben, normal berechnet wurde. Die übrigen 3 wurden durch Veränderungen der Zahlen gebildet. Voraussetzung dafür ist die Tatsache, dass in jeder Reihe und Diagonalen je 2 gerade und 2 ungerade Zahlen zu finden sind. Mag ging nun davon aus, dass die Summe wieder stimmt, wenn die geraden Zahlen um eine Größe reduziert und zum Ausgleich dazu die ungeraden Zahlen um die gleiche Größe erhöht werden.
Durch die Umstellung des Topquadrates, wie es die linke Abbildung zeigt, wurde erreicht, dass die 1. Zelle die Zelle 16 ist. In diese wird die Duosumme abzüglich der Schlüsselzahl für Zelle 1, eingesetzt. Die Berechnung wird dadurch übersichtlicher.
Als erstes mussten die für die Berechnung notwendigen Werte ermittelt werden.
Die Schlüsselzahl ist 8 * 3 = 24 --> gewählt 23. (8 sind die Hunderter der halben Vorgabe. 3 ist rd. 100 / 34, wobei 34 die magische Summe des Topquadrates ist.)
Die Zahl für Zelle 16 ist 1694 / 4 = 423, Rest 2. 423 - 23 (Schlüsselzahl) = 400. (Der Divisor 4 gilt für ein 8er Quadrat, da ja die Vorgabe auch für ein solches gilt.
Der Rest von 2 entfällt auf 2 Topquadrate, d. h. je Quadrat ist der Rest 1, der in einen Block eingesetzt werden muss. Gewählt: Block 3 mit den Zellen 9 bis 12)
Als günstiger Summand für die Veränderung der Zellenzahlen für das 2. und 4. Teilquadrat wird 23 * 2/3 = rd. 16 gewählt und für Teilquadrat 3 wird 23 / 3 = rd. 8 eingesetzt. (Das Dritteln der Schlüsselzahl sichert eine gleichmäßige Streuung der Zahlen und vermeidet Doppelzahlen.)
Als Subtrahenden müssen die gleichen Werte (16 und 8) für die entsprechenden Teilquadrate eingesetzt werden, um so einen Ausgleich zu erreichen.
Zur Ergänzung: Die absteigende Duoreihe wird in die Zellen 16 bis 9 und die aufsteigenden in die Zellen 1 bis 8 eingesetzt. Die Zahlen in den geraden Zellen des Teilquadrates 2 werden um den Wert 16 reduziert und die Zahlen in den ungeraden Zellen um 16 erhöht.
Die Berechnung der Zahlen im Teilquadrat 4 erfolgt in umgekehrter Weise durch Tausch von + und -. Beim 3. Teilquadrat erfolgt die Berechnung wie im Teilquadrat 2, jedoch mit den Werten +/- 8.
Nun kann die erste Zeile des Topquadrates berechnet werden:
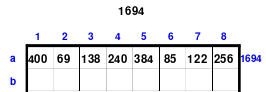
In die Zelle 16 wird der berechnet Wert 400 (1694 / 4 = 423 - 23 = 400) eingesetzt.
Die Zahl für Zelle 3 ist 23 * 3 = 69 und die für Zelle 6 das 2-fache von Zelle 3, das ist 69 * 2 = 138, oder auch 6 * 23 = 138. In die Zelle 9 wird 400 - (16 - 9) * 23 = 239 zu der noch der Rest 1 addiert werden muss, was 240 ergibt.
(Die Berechnung für Zelle 9 dürfte die schwierigste Rechenaufgabe in diesem Experiment sein!)
Jetzt geht es weiter mit der 1. Zeile im 2. Teilquadrat.
Die Zelle 5a ist die Zelle 16, eine gerade, in die 400 - 16 = 384 kommt.
Die nächste Zelle (3), ist eine ungerade und folglich wird hier der Wert 69 + 16 = 85 eingetragen. Dann in Zelle 7a, Zelle 6, eine gerade, 138 - 16 = 122 und in die Zelle 8a, Zelle 9, eine ungerade, 240 + 16 = 256.
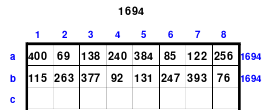
Bei der Berechnung der 2. Zeile im Ausgangsquadrat wird vereinfacht auf die Werte in Zeile 1 zugegriffen.
Die Zelle 1b ist die Zelle 5 und um 1 mal 23 kleiner als die Zahl in Zelle 3a, der Zelle 6. Es wird gerechnet: 138 - 23 = 115.
Die Zelle 2b, die Zelle 10 ist um 1 größer als Zelle 9 in 4a. Folglich 240 + 23 = 263 für Zelle 2b.
Aber Achtung!
Die Zelle 4a und jetzt auch 2b enthalten zusätzlich den Rest und dürfen deshalb nur für die Zahlen der Zellen des 3. Blockes (9 bis 12) herangezogen werden.
Weiter zur Zelle 3b, die Zelle 15 mit der Zahl 400 - 23 =377 und
Zelle 4b, die Zelle 4 im Basisquadrat, ist um 1 größer als die 3 in Zelle 2a. Es ist zu rechnen 69 + 23 = 92.
Jetzt können die Zahlen in das Teilquadrat 2 eingetragen werden.
Die Zelle 5b ist die Zelle 5, eine ungerade, deshalb 115 + 16 = 131.
Zelle 6b, Zelle 10, gerade, 263 - 16 = 247.
Zelle 7b; Zelle 15, ungerade, 377 + 16 = 393 und
Zelle 8b, Zelle 4, gerade, 92 - 16 = 76.
So wird weiter verfahren, bis die Zeilen a bis d ausgefüllt sind.
Beim Übergang zum 4. Teilquadrat wird aus + 16 jetzt - 16, wobei auf die Zahlen im 1. Teilquadrat Bezug genommen wird.
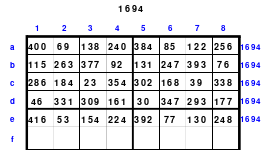
Nachfolgend die Berechnungen in gekürzter Form:
In Zelle 1e (Zelle 16, gerade) 400 + 16 = 416.
In Zelle 2e (Zelle 3, ungerade) 69 - 16 = 53.
In Zelle 3e (Zelle 6, gerade) 138 + 16 = 154 und
in Zelle 4e (Zelle 9, ungerade) 240 - 16 = 224.
Für die Berechnung der Zahlen für das Teilquadrat 3 stehen mehrere Varianten zur Verfügung. Es kann gewählt werden zwischen gerade Zellen + 8 und ungerade Zellen - 8, oder umgekehrt. Als Bezugsquadrat kann zwischen den Teilquadraten 1; 2 und 4 gewählt werden.
Mag hat gewählt: Gerade Zellen + 8, ungerade - 8 und als Bezugsquadrat das Teilquadrat 2.
Daraus ergeben sich folgende Zahlen für die 1. Zeile im Teilquadrat 3:
Für Zelle 5e (16 gerade, Bezug zu 5a) 384 + 8 = 392,
für Zelle 6e (3 ungerade, Bezug 6a) 85 - 8 = 77,
für Zelle 7e (6 gerade, Bezug 7a) 122 + 8 = 130 und
für Zelle 8e (9 ungerade, Bezug 8a) 256 - 8 = 248.
In gleicher Weise werden die Zahlen für die Zeilen f; g und h berechnet.
Das fertige Quadrat ist magisch mit der magischen Summe 1694 entsprechend der Vorgabe.
Es ist das am Anfang auf der ersten Seite abgebildete Quadrat.
Eine Analyse
Nach einer Betrachtung des Ergebnisses stellte Mag fest, dass die Eigenschaften des Topquadrates trotz der Manipulationen erhalten geblieben sind.
So haben die blau gekennzeichneten 2 mal 2 = 4 Zellen großen Quattros die magische Summe eines Teilquadrates von 847. Lediglich die rot dargestellten Quattros haben nicht die magische Summe von 847. Deren Summen weichen mit +1 und -1 davon ab. Das ist verständlich, wenn man das links abgebildete Topquadrat betrachtet. Im linken roten Quattro sind mit 10 und
11 zwei Zellen vorhanden, zu denen der Rest von 1 zugeschlagen wurde. Im rechten Quattro ist dagegen keine Zelle des 3. Blockes (Zellen 9 bis 12) enthalten.
Die in den einzelnen Teilquadraten gekennzeichneten Quattros treffen auf alle 4 Teilquadrate zu.
Schlussfolgerung daraus ist, wenn es möglich ist, Reste zu vermeiden, dann haben alle möglichen Quattros innerhalb der Teilquadrate als Summe die magische Summe der Teilquadrate, auch die rot gekennzeichneten.
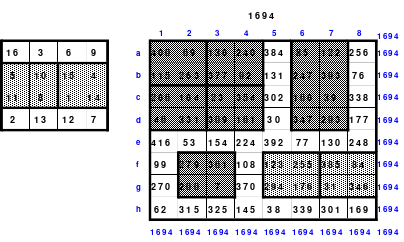
Diese Erkenntnisse lassen die verworfene Ursprungsvariante in einem neuen Licht erscheinen und es ergeben sich annehmbare Varianten durch Nutzung in leicht veränderter Form. Die Ursprungsvariante erläutert Mag in der folgenden “Alternative”.
Eine Alternative
Mag stellt die Ursprungsvariante vor, die er damals zur Familienfeier erdacht hatte. Da es fast unmöglich ist, nach einer brauchbaren Regel einen Rest in das Quadrat der 8. Ordnung einzuarbeiten, musste die Vorgabe unbedingt eine gerade Zahl sein. Mag bat um eine größere 3-stellige Zahl, die er über das linke Teilquadrat schrieb.
Angenommen es war die Zahl 847. Danach schrieb er über das Gesamtquadrat die Zahl 1694, das ist das Doppelte von 847. Damit war die magische Summe des 8er Quadrates eine gerade Zahl.
Die Berechnungen erfolgten wie im Meisterquadrat beschrieben.
Nach der Fertigstellung des Quadrates erklärte Mag, dass alle 4 Teilquadrate die vorgegebene Summe von 847 haben und dass diese magisch sind. Denn alle waagerechten und senkrechten Reihen und auch die Diagonalen haben alle die gleiche Summe von 847 und sind damit magisch. Diese 4 Teilquadrate ergeben zusammen ein magisches Quadrat der 8. Ordnung mit der magischen Summe von 1994.
Später fand er diese Form der Ausführung als kritisch.
Die Erklärung, dass die 4 Teilquadrate auch magisch sind verrät schon halb das Geheimnis der Lösung. Auch eine lineare Unterteilung in die 4 Teilquadrate sollte vermieden werden. Es sollte ausschließlich der Eindruck bestehen, dass nur ein Quadrat der 8. Ordnung erstellt wird. Folglich sollte ein Verweis auf die magischen Teilquadrate nicht erfolgen. Auch sollte die Vorgabe die des Gesamtquadrates sein, da die Frage gestellt werden kann, weshalb nicht gleich die Vorgabe für das 8er Quadrat erbeten wird.
Diese Bedenken kann man zerstreuen. Dazu müssen nur die Quattros in den Mittelpunkt gestellt werden. Nach Fertigstellung eines Quattros weist man daraufhin, dass dieser als Summe der Vorgabe entspricht. Das wird bei weiteren Quattros mehrfach betont. Es muss der Eindruck entstehen, dass es um die Bildung der Quattros geht. Ist ein Teilquadrat fertig, kann darauf hingewiesen werden, dass auch die 4 Zahlen jeder waagerechten und senkrechten Reihe dieses Teilquadrates ebenfalls die Vorgabe als Summe haben. Dabei sollte nicht darauf hingewiesen werden, dass es sich um magische Quadrate handelt. Nach Fertigstellung wird auch darauf verwiesen, dass auch die Reihen des 4 mal 4 großen Quadrates in der Mitte (Spalten 3 bis 6 und Zeilen c bis f) die Summe der Vorgabe haben.
Erst zum Schluss wird dann auf das magische Quadrat der 8. Ordnung eingegangen, so als wäre es ein Ergebnis der Quattrobildung.
Um die Quattros stärker in den Fokus zu rücken, hat er die Bildung eines Quadrates erdacht, bei dem das Quadrat der 8. Ordnung deutlich aus Quattros erstellt wird. Diese Variante nennt Mag “Das Mosaikquadrat”
Das Mosaikquadrat
In den vorangegangenen Darlegungen wurde immer die 1. Zeile des Ausgangsquadrates berechnet und dann weiter die gesamte 1. Zeile des 8er Quadrates. So wurde das 8er Quadrat Zeile um Zeile aufgebaut.
Im Mosaikquadrat werden nacheinander 2 mal 2 Zellen große Quattros mit Zahlen ausgefüllt, wobei deren Summen stets die Größe der Vorgabe haben. Die Reihenfolge der Eintragungen scheint dabei nicht nach einer Regel zu erfolgen. So wird ein Quattro nach dem anderen gebildet, bis das gesamte Quadrat der 8. Ordnung fertig gestellt ist.
Zum besseren Verständnis hat Mag die Parameter der vorangegangenen Berechnungen übernommen. Lediglich die Vorgabe hat er um 1 reduziert, um so eine gerade 3-stellige Vorgabe zu erhalten. Dadurch können Sie sich davon überzeugen, dass alle Quattros der 4 Teilquadrate als Summe die Vorgabe haben.
Die Parameter für die Berechnungen werden ausschließlich aus der Vorgabe gebildet.
So ist die Schlüsselzahl 8 * 3 = 24, gewählt 23. (Diese Zahl muss man sich merken.)
Die Plus/Minus-Werte sind für die Teilquadrate 2 und 4, 2 * 23/3 = rd. 16 und für das Teilquadrat 3 ist der Wert +/-8. (Diese Werte ebenfalls merken.)
Die Bezugsquadrate werden wie gehabt gewählt. Das ist für Teilquadrat 2 +/- 16 der Werte aus dem Ausgangsquadrat, dem Teilquadrat 1, für das Teilquadrat 4 -/+16 gegenüber dem Ausgangsquadrat und für das Teilquadrat 3 +/-8 gegenüber dem Teilquadrat 2.
Grundlage der Berechnungen ist das unveränderte Topquadrat wie es links abgebildet ist. Das rechte Quadrat zeigt eine mögliche Reihenfolge der Quattrobildung. Sie ist nicht verbindlich. Es gilt der Grundsatz, dass vorher das entsprechende Quattro im Bezugsquadrat berechnet wurde. (Ist doch logisch!).
Die Wahl der Reigenfolge sollte jedoch so gewählt werden, dass nicht ständig 2 Quattros weiter gegangen wird. Es ist nicht notwendig, sich eine Reihenfolge zu merken. Die Entscheidungen dazu können operativ gefällt werden.
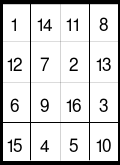
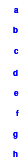
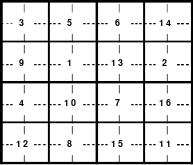
Doch nun zum Beispiel
Mag soll der Akteur sein. Die Vorgabe 846 schreibt Mag über das Quadrat, Dann dahinter die Zahl 1692, das doppelte der Vorgabe, und setzt diese Zahl in Klammern. Damit will er andeuten, dass diese 1692 eine nebensächliche Zahl ist. (Zumindest vorerst.)
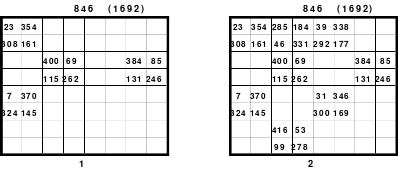
Begonnen wird mit Quattro 1, das sind die Zellen der Spalten 3 und 4, sowie den Zeilen c und d. Im Topquadrat entsprechen diese den Zellen 16; 3; 5 und 10.
In die Zelle 16 wird die Duosumme abzüglich der Schlüsselzahl eingesetzt. Das ist 846/2 = 423, abzüglich 23 = 400. In die Zelle 3 kommt 3 * 23 = 69 und in die Zelle 5 5 * 23 = 115. Die Zelle 10 dürfte die an der schwersten zu berechnenden Zelle sein, jedoch nicht schwierig für einen Rechenkünstler. Die Zellenzahl 10 ist um 6 kleiner als die Zellenzahl 16. Folglich muss von der Zahl in Zelle 16 das 6-fache der Schlüsselzahl abgezogen werden, Das ist 400 – 6 * 23 = 400 - 138 = 262.
(Kommen Sie keinesfalls auf den Gedanken, in die Zelle 10 das doppelte der Zahl aus Zelle 5 einzugeben!)
Mit der Fertigstellung des 1. Quattros bittet Mag die Zuschauer ihre Smartphons zu nehmen, die Rechner-App zu aktivieren und seine Behauptung, dass die Summe der 4 Zahlen der Vorgabe entspricht, zu kontrollieren.
(Damit werden die Zuschauer in die Aktionen einbezogen und Mag erhält evtl. Hinweise zu Fehlern, die er natürlich nicht machen darf!)
Das gebildete Quattro 1 ist nun die Grundlage für die Berechnung des Quattro 2. Das ist für Zelle 7c (16) 400 - 16 = 384, für Zelle 8c (3) 69 + 16 = 85, für Zelle 7d (5) 115 + 16 = 131 und für Zelle 8d (10) 262 - 16 = 246.
Mit der Bildung des Quattro 3 kann auch das Quattro 4 berechnet werden. Die Werte sind für Zelle 1; 23 - 16 = 7, für Zelle 14; 354 + 16 = 370; Zelle 12; 308 + 16 = 324 und für Zelle 7; 161 - 16 = 145.
Der jetzt erreichte Zwischenstand ist im Quadrat 1 festgehalten.
Weiter geht es mit Quattro 5, in das die berechneten Zahlen 285; 184; 46 und 331 eingesetzt werden. In den Spalten 3 und 4 sind erstmals 2 Zahlenreihen mit je 4 Zahlen entstanden. Auch diese Zahlenreihen haben als Summe 846, was die Zuschauer wieder kontrollieren dürfen. Nach Berechnung von nunmehr 8 Quattros ist der erreichte Zwischenstand im Quadrat 2 zu sehen.
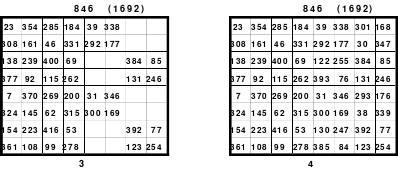
Nach der Fertigstellung des 9. Quattro sind auch in den Zeilen c und d, 2 waagerechte Reihen mit je 4 Zahlen entstanden, deren Summen ebenfalls 846 ist. Wieder können die Zuschauer das kontrollieren.
Das Quadrat 3 zeigt eine Realisierung von 75 %. und das Quadrat 4 das fertige.
(Bitte nicht ständig auf die Summe 846 verweisen mit der Bitte der Kontrolle. Es genügen 2-mal bei einem Quattro und je 1-mal bei einer waagerechten und senkrechten Zahlenreihe.
Bitte sprechen Sie auch nicht von Quattros, sondern von “kleinen Quadraten”.)
Zum Abschluss
erklärt Mag, dass er alle kleinen Quadrate mit einer Summe von 846, wie es die Vorgabe war, gebildet hat.
Es gibt aber auch Weitere, so z. B. dieses, dieses und dieses.
(Dabei umfährt Mag die blauen Quattros. Das trifft für die Quattros in den Spalten 4
und 5, sowie Spalten 7 und 8 nur zu, wenn die Vorgabe eine gerade Zahl ist!!!) Auch die Zahlenreihen mit 4 Zahlen, deren Summen ebenfalls 846 waren, sind nicht die einzigen. Es gibt davon viel mehr. So zum Beispiel die waagerechten und senkrechten Reihen des mittleren 4 mal 4 großen Quadrates, (Auch hier umfährt Mag das rot eingerahmte Quadrat.)
Weiter erklärt Mag, dass es ihm gelungen ist, auch mehrere aus 4 Zahlen bestehenden Reihen mit gleicher Summe, wie gefordert von 846, zu bilden. Es ergeben jeweils 2 dieser Reihen eine Reihe mit 8 Zahlen, die die doppelte Summe, das ist 1692 haben. Wie ich es anfangs über das Quadrat geschrieben habe.
Aber nicht nur alle Spalten und alle Zeilen des Quadrates haben die Summe von 1692, sondern auch die beiden großen Diagonalen.
Damit ist das Quadrat ein magisches Quadrat der 8. Ordnung, in dem keine Zahl doppelt vorkommt.
(Mag hat wissentlich nicht erwähnt, dass auch die 4 Teilquadrate magische Quadrate mit der magischen Summe von 846 sind.)
So, oder auch anders, kann der Abschluss gestaltet werden, was jedem überlassen bleiben sollte. Auch ein Anfang mit einem anderen Quattro ist denkbar.
Mag ist der Auffassung, dass das Mosaikquadrat sehr attraktiv und effektvoll ist und dabei verhältnismäßig leicht erstellt werden kann.
Nicht gerade vorteilhaft ist jedoch die Frage nach einer größeren geraden Zahl. Das kann umgangen werden, indem mehrere Zuschauer um 3- und auch 2-stellige Vorgaben gebeten werden, die zur Gesamtvorgabe addiert werden. Dabei wird zuerst um eine größere 3-stellige Zahl gebeten. Danach um 2-stellige bis die Summe erkennbar eine gerade Zahl wird. Sollte das wider Erwarten nicht der Fall sein, so machen Sie es “noch schwerer”, indem Sie um eine 1- oder 2-stellige Primzahl bitten. Einer Ihrer Zuschauer wird hoffentlich dazu in der Lage sein, anderenfalls helfen Sie nach, in dem Sie einige zur Auswahl nennen. Da Primzahlen immer ungerade Zahlen sind, wird das Ergebnis garantiert ein gerades.
Damit schließt Mag seine Beschreibungen zum Meisterquadrat ab und erklärt, dass er diese Quadrate der 8. Ordnung selbst nicht vorgeführt hat, außer wie gesagt, das Ursprungsquadrat und das nur einmal in einem kleinen familiären Kreis.
6.7.2. Ein gesprungenes Quadrat der 8. Ordnung * *
In einer Fernsehshow (“Klein gegen Groß”) sollte folgende Aufgabe gelöst werden:
In ein Quadrat der 8. Ordnung sollen Zahlen so eingesetzt werden, dass die magische Summe einem vorgegebenen Wert entspricht.
Dabei wurde die Zelle, mit der begonnen werden soll, vorgegeben.
Alle folgenden Eintragungen sollten im Rösselsprung vorgenommen werden.
Der Spieler musste die jeweilige Zellenangabe und die einzusetzende Zahl mit verbundenen Augen nennen.
Seine Angaben wurden elektronisch in ein riesiges Quadrat eingegeben.
Diese Aufgabe wurde von einem 13 Jahre alten Mädchen zügig und fehlerfrei gelöst.
Mag hat sich längere Zeit damit beschäftigt hinter das Geheimnis der Lösung zu kommen. Er hat zwar einige sehr komplizierte Regeln beim Springen gefunden, aber die komplette Lösung blieb ihm verschlossen. Deshalb stellte sich Mag die Aufgabe zumindest eine ähnliche Lösung zu finden. Er hat sie gefunden, allerdings mit qualitativen Einschränkungen. Dafür aber sehr einfach und mit wenigen Rechenkenntnissen lösbar. Auch das Verbinden der Augen wäre möglich, erfordert aber eine sehr hohe Konzentration und Gedächtnisleistung, weshalb Mag von einer derartigen Vorführung abrät.
Eine angenommene Vorführung
Mag erhielt die Aufgabe, ein magisches Quadrat der 8. Ordnung mit einer magischen Summe von 3283 zu erstellen. Das schaffte er in weniger als 10 Minuten. (Am Schreibtisch, denn Mag hat das Quadrat nie vorgeführt!)
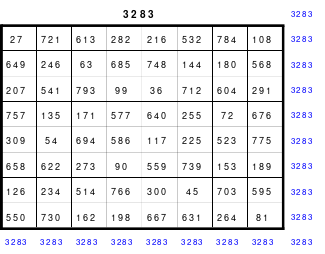
Das gebildete Quadrat ist magisch. Die magische Summe entspricht mit 3283 der Vorgabe. Alle Zahlen sind nur einmal vorhanden. Die kleinste Zahl ist 27 und die größte 793.
Dass das Quadrat nicht pandiagonal ist, hat in diesem Fall keine Bedeutung
Der Ablauf
Nachfolgend eine Beschreibung des Ablaufes, wie es der Zuschauer sieht.
Auf der Tafel befindet sich ein Quadrat der 8. Ordnung, jedoch ohne Zahlen.
Mag bittet um Nennung einer 4-stelligen Zahl. Es wird 3283 genannt, die er über das Quadrat schreibt.
Dann setzt er in die 1. Zelle der 1. Zeile die Zahl 27 ein, in die 3. Zelle der 3. Zeile 793 und anschließend füllte er zügig alle weiteren Zellen mit unterschiedlichen Zahlen aus.
Zum Abschluss erklärt Mag, dass keine der Zahlen doppelt vorkommt und die Summen aller Zeilen, Spalten und Diagonalen der vorgegebenen Zahl 3283 entsprechen. Damit ist das Quadrat ein magisches.
Die Jury kann diese Aussagen nach Kontrolle bestätigen.
Die Berechnungen
Mag wird sich in seinen Ausführungen mehrfach auf das Topquadrat und seine Einordnung in das Quadrat der 8. Ordnung beziehen. Zu ihrer Information ist es nachfolgend dargestellt. (Bei der Vorführung bitte ohne Zahlen und Quadratteilung!)
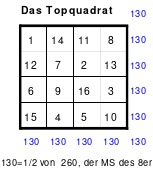
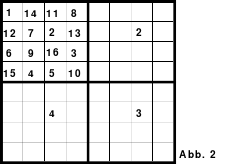
Mag will mit der Darlegung der einzelnen Berechnungen zeigen, wie einfach die Lösung ist und kaum über das kleine Einmaleins hinausgeht. Er will damit Ihr Interesse wecken, sich mit der Materie näher zu beschäftigen. Eine Begründung zu den Rechenschritten erfolgt erst später im Abschnitt “Der Lösungsweg”.
Die einzelnen Rechenschritte beziehen sich nur auf das gezeigte Beispiel:
Mag berechnet die Schlüsselzahl mit 3*4=12 und wählt 9 als die bessere Schlüsselzahl.
Er setzt in die Zelle 1 des 1. Teilquadrates (oben/links) die Zahl 27 ein.
Mag berechnet die Duosumme mit 3283 / 4 = 820 und Rest 3, der gleichzeitig der Endrest ist. Er zieht von der Duosumme die Zahl aus Zelle 1 = 27 ab und erhält 793, die er in die Zelle 16 einsetzt.
Jetzt kann mit der Eintragung weiterer Zahlen in das Quadrat begonnen werden.
Alle folgenden Zahlen werden im Uhrzeigersinn eingetragen. Links oben ist das Quadrat 1, das Starterquadrat. Rechts davon das Quadrat 2, darunter das 3. Quadrat und links davon das Quadrat 4. Von dort geht es nach oben wieder zum Quadrat 1, dem Starterquadrat. Dabei sind die Schritte von Quadrat zu Quadrat nicht einheitlich. Von den Quadraten 1 nach 2 und von 3 nach 4 geht es im Doppelsprung, 4 waagerecht und 2 senkrecht und von den Quadraten 2 nach 3 und 4 nach 1 geht es im Langsprung, 4 senkrecht und nur1 waagerecht. Dabei gelten folgende Regeln. Beim Doppelsprung wird die Bewegung 2 senkrecht zur Außenlinie vorgenommen. Sind keine 2 Zellen Abstand bis zur Außenlinie vorhanden, so erfolgt die Bewegung nach innen. Analog verhält es sich bei den Langsprüngen. Hier wird die waagerechte Bewegung 1 nach außen vorgenommen. Ist das nicht möglich, geht es 3 nach innen. Werden alle Eintragungen entgegen dem Uhrzeigersinn vorgenommen, ändern sich bei den Langsprüngen die waagerechten Bewegungen zu 3 nach außen und im Verhinderungsfall 1 nach innen.
Die ersten 32 Zahlen werden als absteigende arithmetische Reihe eingetragen. Das sind die Zellen 16 bis 9. Die Differenz zwischen den Gliedern der Reihe beträgt entsprechend der Schlüsselzahl 9.
Begonnen wird mit Zelle 16 des 1. Quadrates, dem Starterquadrat. Dort ist bereits die 793 eingetragen. Von dort geht es im Doppelsprung in das 2. Quadrat wo die um 9 reduzierte Zahl 784 geschrieben wird, Dann weiter im Langsprung zum 3. Quadrat wo eine 9 kleinere Zahl, also 775 eingesetzt wird. Weiter im Doppelsprung zum 4. Quadrat mit der Zahl 766. Von dort geht es im Langsprung zurück zum Starterquadrat. Da hier die Zelle bereits eine Zahl enthält geht es zur nächsten niederen Zelle, der Zelle 15 im Topquadrat, in die 757 einzusetzen ist. Von dort wie gehabt zu den Quadraten 2, 3 und 4, in die nacheinander die Zahlen 748, 739 und 730 eingetragen werden. So wird weiter verfahren, bis alle Zellen von 16 bis 9 abgearbeitet sind.
Die nächsten 32 Zahlen werden als aufsteigende arithmetische Reihe mit der gleichen Differenz von jetzt plus 9 eingesetzt. Begonnen wird in Zelle 1 des Starterquadrates in der sich bereits die Zahl 27 befindet. In die im Springen erreichten Zellen in den Quadraten 2, 3 und 4 werden die jeweils um 9 erhöhten Zahlen 36, 45 und 54 eingeschrieben. Jetzt erfolgt das Gleiche mit der Zahl 63 für Zelle 2 des Starterquadrates. In die Quadrate 2, 3 und 4 werden nach Doppel- oder Langsprung die Zahle 72, 81 und 92 geschrieben. So wird weiter verfahren, bis alle Zellen eine Zahl enthalten.
Aber Achtung!
Beim Übergang von der Zelle 6 in die Zelle 7 beginnt die zusätzliche Erhöhung um den Rest 3. Dazu wird die Zahl für Zelle 7 des Starterquadrates zusätzlich um 3 erhöht. Das ist, ausgehend von der letzten Zahl für Zelle 6 im 4. Quadrat = 234, 234 + 9 + 3 = 246. Die weiteren Zahlen werden dann nur noch um 9 erhöht.
Damit ist das magische Quadrat der 8. Ordnung fertig. Es ist magisch, aber wegen der Einordnung des Restes nicht pandiagonal.
Wie eingangs erwähnt, ist die Berechnung sehr einfach und ohne Probleme lösbar. Das Schwierigste dürfte dabei lediglich das Erlernen der Zahlenfolge des 4er Topquadrates und das Beherrschen der richtigen Sprünge sein, was aber ohne weiteres machbar ist.
Allerdings ist ein hohes Maß an Konzentrationsfähigkeit Bedingung. Wenn bei der Subtraktion oder Addition des Wertes 9 von den vorherigen 2- bis 4-stelligen Zahlen ein Fehler gemacht wird, pflanzt sich der Fehler bis zum Ende der jeweiligen arithmetischen Reihe fort. Damit ist die Erstellung des magischen Quadrates gescheitert! Eine Fehlerfindung und Korrektur sind äußerst schwierig!
Eine weitere Schwierigkeit dürfte die Einordnung des Restes sein, der ja in jeder Reihe einmal enthalten sein muss.
Der Lösungsweg
Mag war sich im Klaren, das eine Lösung mit einem Quadrat der 8. Ordnung nur schwer zu realisieren ist. Es müssten nämlich alle 64 Zellen und ihre Einordnung bestens beherrscht werden. Deshalb suchte er von Anfang an nach einer Lösung mit dem Topquadrat, einem magischen Quadrat der 4. Ordnung. Es musste 2 * 2 = 4-mal zu einem Quadrat der 8. Ordnung zusammengestellt werden. Dabei ist Bedingung, dass diese 4 Teilquadrate alle die gleiche magische Summe haben müssen. Das bedeutet, dass die magische Summe der Teilquadrate halb so groß ist als beim 8er Quadrat.
Bei den Methoden zur Bildung magischer Quadrate wird Mag die Methode des Pendelns beschreiben, mit der gleichgroße magische Quadrate gebildet und zu größeren Quadraten zusammengefügt werden können. Mag war überzeugt, dass nach dieser Methode, in Verbindung mit der Duomethode, in einer abgewandelten Form eine Lösung zu finden sein müsste, was sich auch bestätigte! Nachfolgend vorab eine Beschreibung der Pendelmethode.
Es werden 4 Topquadrate nebeneinander angeordnet. In die Zellen 1 werden von links nach rechts die Zahlen 1 bis 4 eingesetzt. In die Zellen 2 werden von rechts nach links die nächsten Zahlen 5 bis 8 geschrieben. Dann wieder von der Zelle 3 des 1. Quadrates nach rechts die Zahlen 9 bis 12 und wieder zurück und in die Zellen 4 die Zahlen 13 bis 16 eingeben. So wird fortgefahren bis alle Zellen eine Zahl enthalten. Die magische Summe dieser 4 Quadrate beträgt einheitlich 130, die Hälfte eines Quadrates der 8. Ordnung mit der magischen Summe von 260. Die Quadrate sind magisch und pandiagonal, d. h. auch die geteilten Diagonalen haben 130 als magische Summe.
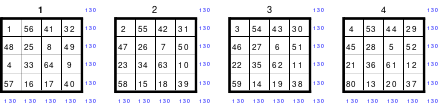
Insgesamt wurde die Hälfte aller Zahlen (32) von links nach rechts und die andere Hälfte von rechts nach links eingesetzt. Folglich muss es auch möglich sein, die 1. Hälfte aller Zahlen von links nach rechts und die 2. Hälfte von rechts nach links einzuschreiben. Das Ergebnis ist das Gleiche, wie nachstehen gezeigten Quadrate es beweisen.
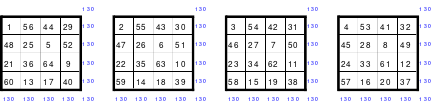
Die Anordnungen der Zahlen entsprechen einer Duoreihe mit 32 Gliedern. Die Duosumme beträgt 1 + 64 = 65.
Um eine bestimmte Größe der Duoglieder zu erreichen müssen die aufsteigenden und absteigenden Zahlenreihen um einen entsprechenden Betrag erhöht werden.
Mag hat ausführlich die Duomethode in der Einführung zum Hexen 1x1 beschrieben.
Bei der Bildung magischer Quadrate ist zwingend erforderlich, dass die Differenzen zwischen den Zahlen eines Blockes einheitlich groß sind. Demzufolge müssen auch die Differenzen zwischen den Zahlen der Duoreihen gleich sein.
Ein wichtiger Hinweis muss jedoch noch gegeben werden. Die Eintragungen erfolgen zuerst von links nach rechts. Betrachtet man die eingesetzten Zahlen, so entsprechen diese einer aufsteigenden Zahlenreihe. Die andere Hälfte wird von rechts nach links eingetragen. Betrachtet man auch die eingesetzten Zahlen von links nach rechts, so entsprechen diese einer absteigenden Reihe. Das bedeutet, dass bei Nutzung der Duomethode, bei der ja die Hälfte aller Zahlen als aufsteigende und die andere Hälfte als absteigende Zahlenreihe zum Einsatz kommen, dass sowohl die aufsteigende als auch die absteigende Zahlenreihe der Duokette, in gleicher Richtung eingetragen werden müssen. Entweder von links nach rechts oder umgekehrt.
Die Schlüsselzahl
Um eine Schlüsselzahl, die ja den Differenzen entsprechen soll, zu berechnen, müsste theoretisch die Vorgabe durch die magische Summe des Basisquadrates geteilt werden. Mag geht einen kürzeren Weg. Er multipliziert die Tausender der Vorgabe mit 4. Das ist möglich, da 1000/260 = rd. 4 ist. Da aber 260 um 10 größer als 250 ist, zieht er vom Ergebnis 1 als Sicherheit ab.
So wird bei einer Vorgabe von 3283 die Schlüsselzahl 3*4-1 gleich 11 ermittelt. Die genutzte Schlüsselzahl kann dann kleiner sein, um ein leichteres Rechnen zu erreichen. In diesem Fall bietet sich die 9 als endgültige Schlüsselzahl an.
Bei einer Vorgabe von z. B. 6178 würde eine günstige Schlüsselzahl 6*4-1=23, gewählt 19 sein.
Natürlich können auch andere Schlüsselzahlen gewählt werden. Das ist abhängig von den möglichen Rechenleistungen jedes Einzelnen. Denkbar wären z. B. Schlüsselzahlen mit den Endziffern 1; 3 oder auch 7.
Die Duosumme
Die Duosumme muss genauestens berechnet werden. Das bedeutet, dass die Vorgabe durch die Hälfte der Ordnungszahl geteilt werden muss. Im Beispiel ist das 3283 / 4 = 820. Es verbleibt ein Endrest von 3. Diese Duosumme ist auf die Zellen 1 und 16, die kleinste Zellenzahl und die größte, zu verteilen. Dabei kann die Zahl für die Zelle 1 größer sein als die Schlüsselzahl. Allerdings auch nicht zu groß, denn dann kann es zu doppelten Zahlen kommen. Sie kann auch kleiner sein, jedoch mindestens 1.
Kontrolle
Wie bereits beschrieben werden die Zahlen der aufsteigenden Reihe durch ständige Addition der Schlüsselzahl zur vorherigen berechnet, das ist 31-mal. Bei der absteigenden Reihe muss die Schlüsselzahl 31-mal von der vorausgehenden subtrahiert werden. Fehler werden dann bis an das Ende mitgeschleppt.
Eine Kontrolle sollte hier die Fehler rechtzeitig erkennen lassen und so eine evtl. Korrektur ermöglichen.
Die Starterzahlen im Starterquadrat können zur Kontrolle berechnet werden. Zum Beispiel ist bei der aufsteigenden Reihe die folgende Zellenzahl um 4-mal die Schlüsselzahl größer als die vorherige. Bei der absteigenden Reihe muss von der vorherigen das 4-fache der Schlüsselzahl abgezogen werden.
Natürlich ist auch die direkte und damit genauere Berechnung möglich, aber etwas aufwendiger.
So für die aufsteigende Zahlenreihe: Zn = Z1 + (ZNn - 1) * 4 * SZ
und für die absteigende Zahlenreihe: Zn = Z16 - (16 - ZNn) * 4 *SZ
Es bedeuten: Zn = Zellenzahl für die Zelle n
Z1 / Z16 = Zahl in Zelle 1 bzw. 16
ZNn = Zellennummer der Zelle n
SZ = Schlüsselzahl
Das Quadrat
Das weiter vorn abgebildete 8er Quadrat (Abb. 2) zeigt die 4 Topquadrate, die zu einem Quadrat der 8. Ordnung zusammengesetzt sind. In dieser Form kann das Quadrat jedoch nicht verwendet werden. Die Bewegungen von Quadrat zu Quadrat würden stets die Umrundung eines Quadrates sein. Je 4 Zellen waagerecht und 4 senkrecht. Doch das ist nicht das Hauptproblem. Dieses ist die Verteilung des Restes! Es gibt dafür keine Regel, wie bei dem Top- oder Pentaquadrat, wo der Rest den Zahlen des letzten Blocks zugeschlagen werden kann. Eine Lösung stellt die blau markierten Zellen dar, die aber in einer Vorführung keinesfalls von Nutzen ist.
Mag löste das Problem, indem er die Quadrate 2, 3 und 4 umstellte. Im Quadrat 2 verschob er 2 Zeilen von oben nach unten, im Quadrat 4 verschob er die rechte Spalte nach links und im Quadrat 3 übernahm er die Veränderungen von den Quadraten 2 und 4. Die Veränderung ist im Quadrat 2 dargestellt.
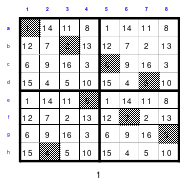
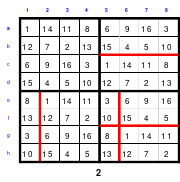
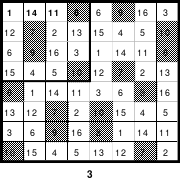
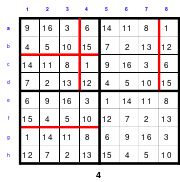
Das Quadrat 3 zeigt das Ergebnis dieser Veränderung. Insgesamt sind 4 Zahlenpaare zu finden, die auf jeder Reihe wirksam werden. Davon sind die Zahlenpaare 7 mit 8, sowie 10 mit 9 von Bedeutung. 7 und 8 sind die letzten Zahlen der aufsteigenden Duo-Zahlenreihe. Der Rest wird nur einmal der Zahl für Zelle 7 des Starterquadrates zugeschlagen. Danach geht es bis zur Abarbeitung der Zellen 8 nur mit der Addition der Schlüsselzahl weiter. Da die Zellen 8 die letzten in der aufsteigenden Reihe sind, entfällt eine Zurücksetzung des Restes.
Genauso verhält es sich mit dem Zellenzahlen 10 und 9. Diese Zellen sind die letzten zu berechnenden Zellen der absteigenden Duo-Zahlenreihe. Bei diesen Zellen wird nicht nur die Schlüsselzahl abgezogen, sondern auch der Rest zugeschlagen bzw. nur die um den Rest reduzierte Schlüsselzahl abgezogen. Diese Manipulation wird nur bei der Berechnung der Zahl für Zelle 10 des Starterquadrates vorgenommen. In der Folge wird nur die unveränderte Schlüsselzahl abgezogen. Die Zellen 9 der Teilquadrate sind zugleich die letzten Zellen der absteigenden Zahlenreihe.
Die Veränderungen der Teilquadrate bringen einen weiteren Vorteil. Die Bewegungen von Quadrat zu Quadrat sind nicht mehr nur 4 gerade, sondern sind wie bereits beschrieben Doppelsprung in der waagerechten und Langsprung in der senkrechten Bewegung.
Machen Sie sich mit den Bewegungen im Quadrat 3 vertraut.
Die Umstellung der Quadrate müssen Sie sich nicht merken. Dafür aber die Sprünge. Werden diese richtig vorgenommen, ergibt sich die Veränderung automatisch. Das trifft auch dann zu, wenn ein anderes Quadrat als Starterquadrat eingesetzt wird. Im Quadrat 4 wurde das Teilquadrat 3 als Starterquadrat gewählt.
Eine Nachbetrachtung
Die gestellte Aufgabe, ein magisches Quadrat der 8. Ordnung mit einer vorgegebenen magischen Summe und unterschiedlichen Zahlen zu bilden wurde erfüllt. Das Ergebnis ist beachtlich (zumindest für den Außenstehenden) und verbietet eigentlich jede Kritik. Es geht auch nicht um eine Kritik am Quadrat, sondern um das Problem einer Nutzung des Wissens. Betrachten Sie das Nachfolgende mehr als Bemerkungen zum Thema.
Es fällt auf, dass im Beispiel Zahlen der 400er Reihe fehlen. Der Grund ist, dass die grob ermittelte Schlüsselzahl 11 ist, aber aus rechentechnischen Gründen die 9 gewählt wurde.
Das könnte vermieden werden, in dem die Duosumme auf die Zellenzahlen 8 und 9 des Starterquadrates verteilt wird. Im Beispiel könnte 820/2-9=401 für die 8. Zelle und 820/2+9=419 für die 9. Zelle gewählt werden.
Auf diese Variante kann man verzichten und nimmt den kleinen Schönheitsfehler, den ohnehin kaum jemand erkennt, in Kauf. Allerdings sollte die Schlussfolgerung sein, die Schlüsselzahl nicht zu klein wählen.
Sie sollte aber auch nicht zu groß sein, um die Gefahr von doppelten Zahlen auszuschließen.
Wer es genauer machen will, der teilt die Duosumme durch 2 und erhält den Mittelwert. Zieht man von diesem Mittelwert 32-mal die gewählte Schlüsselzahl ab, so erhält man einen besseren Wert für die Zelle 1. Die Zahl für die Zelle 16 ist dann Duosumme abzüglich Zahl für Zelle 1.
In den Beispielen wäre das 820/2=410 Weiter 410-32*9=122 für Zelle 1 und 820-122=698 für Zelle 16. Die größte Zahl der aufsteigenden Reihe wäre dann 122+31*9=401 und die kleinste der absteigenden Reihe 698-31*9=419.
Damit ist die Zahlenlücke bis auf eine Differenz von 18 geschlossen.
(Lohnt sich dieser Aufwand überhaupt?)
Die ständige Erhöhung oder Verminderung der Zahlen um jeweils 9 ist leicht zu erkennen. Deshalb sollte eine größere Schlüsselzahl das Ziel sein. Bei der Bitte um eine 4-stellige Zahl, sollte um eine höhere 4-stellige Zahl gebeten werden. Ab einer Vorgabengröße 5000 kann die Schlüsselzahl mit 19 und größer gewählt werden.
Eine Alternative
Mag kann verstehen, dass die Lösung für manchen noch als schwierig betrachtet wird. Er hat deshalb eine alternative Lösung erarbeitet, die weniger kompliziert ist.
Ist die Vorgabe durch 4 teilbar, dann fällt kein Rest an. Daraus ergeben sich nicht nur rechnerische Vorteile, sondern weitere, da nicht mehr berücksichtigt werden muss, dass das Topquadrat nur teilhomogen ist. Mag wird diese Vorteile noch nennen. Ziel ist es folglich, eine durch 4 teilbare Vorgabe zu erhalten. Die Bitte, eine Vorgabe mit 4 zu multiplizieren, kommt etwas zu plump daher.
Zwar auch nicht ganz seriös, aber noch annehmbar, ist folgender Vorschlag:
Man bittet um eine höhere 3-stellige Zahl.
Mit den Worten: “Heute fühle ich mich gut drauf und könnte eigentlich mal was größeres versuchen. Machen wir doch aus der 3-stelligen Zahl eine 4-stellige.” wird eine Ziffer an die 3-stellige Zahl angehängt. Diese wird so gewählt, dass eine durch 4 teilbare Zahl entsteht. Sollte die Vorgabe bereits durch 4 teilbar sein, so ist sie mit der 4 oder 8 zu ergänzen, da eine nur 3-stellige Zahl für das Experiment zu klein ist.
Die Vorteile der so manipulierten Zahl sind:
Es fällt kein Rest an und erleichtert so die Berechnungen.
Der Zuschauer kann eine Zelle bestimmen, mit der begonnen werden soll. Damit bestimmt der Zuschauer das Starterquadrat und eine Umstellung dieses durch notwendige Verschiebungen von Zeilen und/oder Spalten. Das setzt natürlich eine beste Kenntnis des Topquadrates voraus.
Der fehlende Rest ermöglicht auch die Anwendung einfacher umgestellter Teilquadrate. Dabei werden im Gegensatz zum weiter vorn dargestellten Quadrat 2 das Teilquadrat 2 senkrecht und das Teilquadrat 4 waagerecht geteilt. Das Teilquadrat 3 wird sowohl waagrecht, als auch senkrecht halbiert. Siehe hierzu das Quadrat 5.
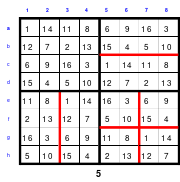
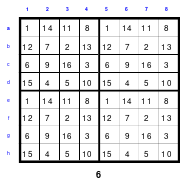
Das Wichtigste dieser Veränderung ist der Wegfall des Langsprunges. Alle Sprünge werden nur noch als Doppelsprung vorgenommen.
Rein theoretisch könnte auf die Umstellung der Teilquadrate verzichtet werden und das Quadrat in Abbildung 6 einsetzen. In diesem Fall würde die richtige Zelle im folgenden Teilquadrat durch ein Weiterrücken um 4 Zellen in gerader Linie erreicht. Eine solche Variante lehnt Mag als zu primitiv ab.
Schlussbemerkung
Oft wird die Frage gestellt: “Lohnt sich überhaupt der Aufwand, da eine Vorführung in einem größeren Kreis (Bühne) ohnehin kaum möglich ist?” Es fehlt beispielsweise an
einer entsprechend großen Tafel. Diese müsste ca. 2,5 mal 2 m groß sein, um die 8 mal 8 = 64 Zellen wenigstens in der Größe eines A4-Blattes darstellen zu können.
(Und wenn eine solche vorhanden ist, sind auch die Arme lang genug?)
Des Weiteren dürfte das Interesse an einer derartigen Darbietung kaum vorhanden sein. Oft ist das Publikum überfordert. Selbst wenn Sie zügig arbeiten, dauert die Vorführung mindesten 10 Minuten und kann dadurch langweilig werden.
Dazu sagt Mag:
“Ein Auftritt mit einem so großen Quadrat muss ja nicht sein.
Es ist doch schön zu wissen, wie so etwas gelöst werden kann. Oder nicht?”
6.7.3. Fantastisch * *
Mag hat mit dem “Meisterquadrat” und “Gesprungenes 8er Quadrat” zwei akzeptable Lösungen für Quadrate der 8. Ordnung im Hexen 1x1 beschrieben.
Mag war damit nicht ganz zufrieden, denn sie waren nicht so attraktiv wie die Darbietung in der TV-Sendung ”Klein gegen Groß”. Mag hat nach weiteren, besseren Lösungen gesucht und eine weitere gefunden, die zwar nicht der Darbietung in ”Klein gegen Groß” entspricht, aber qualitativ dieser durchaus gleich zu stellen ist.
So kann, als eine der möglichen Varianten dieser Routine, der Akteur sich abseits mit verbundenen Augen befinden und lässt sich nur die Zellen nennen, in die die nächste Zahl eingesetzt werden soll. Er findet die richtige Zahl für diese Zelle und lässt sie dort einsetzen. So wird verfahren, bis das Quadrat fertig ist. Es ist magisch und die magische Summe entspricht der Vorgabe.
Als Einführung in diese Routine zeigt Mag als erstes die Bildung eines Quadrates der 8. Ordnung, dass aus einer Zahlenvorgabe erstellt wurde.
Dazu bat der Akteur um eine 2-stellige Zahl. Es wurde die 48 genannt, die der Akteur in die erste Zelle einsetzte. Nach einem kleinen Moment schrieb er über das Quadrat die Zahl 636. Anschließend füllte er alle Zellen zeilenweise mit unterschiedlichen Zahlen aus, bis das Quadrat fertig war. Es ist ein magisches Quadrat mit der magischen Summe von 636, wie sie zuerst über das Quadrate geschrieben wurde.
Diese Aufgabe wurde in weniger als 10 Minuten gelöst und dürfte sogar in 5 Minuten zu realisieren sein.
Das Quadrat ist auch pandiagonal, was aber nicht erwähnt wurde.
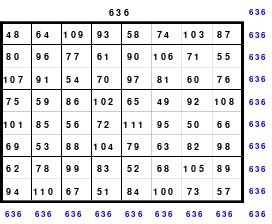
Als Mag im Abschnitt “Kleine Schule” die Fusionsmethode einarbeitete, kam ihm die Erkenntnis, dass sich die Fusionsquadrate hervorragend für das Hexen 1x1 eignen, zumindest die nicht allzu großen.
Die Fusionsquadrate sind magische Quadrate deren Zellen durch weitere, zu Wechselquadraten umgestaltete Quadrate, ersetzt werden, wobei die einzufügenden Wechselquadrate keine magische sein müssen. Selbst die 4-zelligen Quattros sind dafür geeignet. Die Bildung solcher Quadrate wurde im Abschnitt “Fusionsmethode” behandelt.
Mag´s Idee war, 16 Quattros zu Wechselquadrate umzubilden und in das Topquadrat einzusetzen. Dabei wurden die Quattros so eingesetzt, dass deren Nummer mit der Zellenzahl übereinstimmte.
Bei der Bildung von Fusionsquadraten mussten immer die Hälfte der Zeilen- und Spaltenpaare gewendet werden, um so die richtigen Zeilen- und Spaltensummen zu erhalten. Dabei mussten bei den einfach geraden Quadraten die Hälfte von Quattros gewendet werden, was zur Auflösung deren Struktur führte.
Diese Strukturen sind aus den folgenden Abbildungen ersichtlich.
Die kleinste Zahl entspricht der Zellenzahl im Topquadrat. Alle folgenden Zahlen sind um jeweils 16, der Ordnungszahl des Topquadrates, größer. Die Zahlenanordnung entspricht einem Z (als Eselsbrücke).
Die beiden Diagonalen im Quattro sind gleich groß, weshalb es gewendet werden kann. Das hat Bedeutung beim Einsatz eines Quattros in die Hauptdiagonalen.
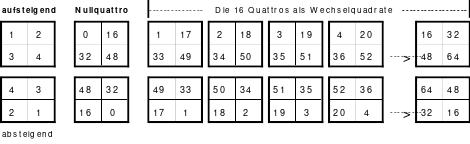
Im 8er Quadrat entspricht die Hälfte der Zellen in den Zeilen und Spalten die zu wenden wären 4, was mit 2 Quattros abgesichert werden kann.
Mag hat sich entschieden, die geraden Quattros um beide Achsen zu wenden, um so die magische Summe zu sichern. Die untere Reihe der Quattros zeigt die gewendeten. Die Zahlenfolge ist die Gleiche, jedoch als absteigende Zahlenreihe, ebenfalls in Z-form.
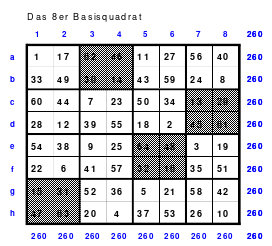
Die Quattros wurden in die Zellen des Topquadrates eingesetzt und das Basisquadrat war geschaffen. Es ist pandiagonal mit der richtigen magischen Summe von 260. Alle Zahlen von 1 bis 64 sind vorhanden und keine Zahl ist doppelt.
Hat man diese Struktur verinnerlicht, so kann jede Zelle bestimmt und berechnet werden. Dazu muss nur das Topquadrat einwandfrei beherrscht werden. Soll z.B. die Zahl in Zelle in 5d berechnet werden, so weiß man, dass es sich um das Quattro 2, ein gewendetes Quattro handelt. Weiter wird erkannt, dass es die 2. Zelle im gewendeten Quattro ist und die Zahl 2+16=18 groß ist.
Weitere zu beachtenden Regelmäßigkeiten, die eine Vereinfachung der Berechnungen zulassen, werden im Beispiel der Zahlenvorgabe von 48 erklärt.
Die 48 wird in die erste Zelle eingesetzt. In dieser steht normalerweise die 1, die folglich um 47 größer wurde. Diese 47 wird als Summand allen Zellen zugeschlagen.
Die magische Summe wird dadurch um 8*47=40*8=320+7*8=56=376 größer, das ist 260+376=636, was als magische Summe über das Quadrat geschrieben wird.
Anschließend werden die Zahlen für alle Zellen zeilenweise berechnet und eingetragen.
Das ist als nächste Zelle die Zelle 2 im 1. Quattro. Diese ist 1+1*16=17+47=64 groß.
Es folgt das Quattro 14, ein gewendetes mit der größten Zahl dieses Quattro (denken Sie an das Z!) Die Zahl ist 14+3*16=14+48=62+47=109. Die nächste Zelle gehört noch zum Quattro 14 und hat die Zahl 14+2*16=14+32=46+47=93. Weiter geht es mit Quattro 11, ein nicht gewendetes, mit den Zahlen 11+47=58 und 11+1*16=27+47=74. Das letzte Quattro in dieser Zeile ist das gewendete Quattro 8 mit den Zahlen 8+3*16+47=103 und 8+2*16+47=87. So kann Zeile um Zeile abgearbeitet werden bis das Quadrat mit Zahlen ausgefüllt ist. Das Quadrat ist magisch mit der magischen Summe von 636.
Mag hat bewusst die einzelne Berechnung jeder Zelle vorangestellt, weil sie bei der schwierigsten Variante notwendig wird. Bei den leichteren Varianten können Vereinfachungen der Berechnung genutzt werden, diese sind:
Jede 2. Zahl in der Zeile ist im angewendeten Quattro um 16 größer. Bei den gewendeten Quattros sind diese um 16 kleiner.
In der 2. Zeile sind die Zahlen um 32 größer oder kleiner als die Zahl in der darüber befindlichen Zeile, je nach dem es sich um gewendete oder nicht gewendete Quattros handelt.
Im Grunde genommen reichen die Berechnungen der 1. und 3. Zahl in der 1. Zeile aus, um die Zahlen für alle anderen Zellen zu ermitteln. So sind die Zahlen im Quattro 11 um 10 größer als im Quattro 1 (11-1=10). Beide sind angewendete Quattros. Im Quattro 9 sind sie um 9-1=8 größer als im Quattro 1, oder auch um 2 kleiner als im Quattro 11, dass ja ebenfalls ein angewendetes ist. Gleiches trifft auf die gewendeten Quattros zu. So sind die Zahlen im Quattro 8 um 6 kleiner als in Quattro 14 und im Quattro 12 um 4 größer als im Quattro 8 oder um 2 kleiner als im Quattro 14.
Aber Achtung!
Bei Entstehung eines Restes, der den Quattros 13 bis 16 zugeschlagen werden muss, kann die Bezugnahme nur zwischen Quattros ohne oder mit Restzurechnung erfolgen. Deswegen müssen die Quattros 8 und 13 komplett berechnet werden. Diese sind das erste gerade Quattro ohne Restzuschlag bzw. das erste ungerade mit Restzuschlag in der Reihenfolge.
Die Grundvariante ist ausreichend erläutert und es kann zu weiteren Varianten übergegangen werden.
Variante 2
Um ein leichteres Rechnen zu ermöglichen, kann der Summand zu einer günstigeren Zahl manipuliert werden. Das erfolgt in der Regel durch Reduzierung der Vorgabe auf eine Zehnerzahl und Einsatz dieser in das Quattro, das der Reduzierung entspricht. Das wäre im Beispiel mit der Vorgabe 48 die Reduzierung auf eine Vorgabe 40 und Einsatz der 40 als kleinste Zahl in das Quattro 8. Die magische Summe wird dann 40*8+260=580.
Das Quattro 8 ist jedoch nicht günstig. Die Zahl 8 befindet sich im gewendeten Quattro nicht in der 1., sondern der 4. Zelle und kann damit nicht als Zelle 1 gelten, es sei denn man nimmt eine Auflösung des Quattro 8 und weitere in Kauf. Das ist zwar möglich, denn das Quadrat ist ja ein pandiagonales, aber hat ein unerwünschtes Umdenken des Systems zur Folge, was verhindert werden sollte. Es ist deshalb besser, die Reduzierung so vorzunehmen, dass der manipulierte Summand in ein nicht gewendetes, also ungerades Quattro eingesetzt wird. Das wäre mit einer Reduzierung der Vorgabe um Endziffer +/-1 gegeben. Im Beispiel 48-7=41 (40+1) oder 48-9=39(40-1), Mit diesen Summanden kann ebenfalls einfacher gerechnet werden. Der Summand wird dann in die 1. Zelle des Quattro 7 oder 9 eingesetzt. Die magische Summe muss neu berechnet werden. Sie ist um 8 größer oder kleiner 580.
Variante 3
Bei dieser Variante erfolgt die Eintragung der Zellenzahlen nicht zeilenweise, sondern in von den Gästen bestimmte Zellen. Dazu sind die Zeilen und Spalten mit den Zahlen von 1 bis 8 zu kennzeichnen. Die Zahlen für die Zellen müssen einzeln berechnet werden, da ein Bezug auf bereits berechnete Zellenzahlen unmöglich ist.
Diese Variante kann mit der Variante 2 gekoppelt werden, was aber zu einer zusätzlichen Belastung führt.
Wird die Vorgabe genannt, so wird sie um 1 reduzieret und als Summand für alle Berechnungen eingesetzt. Als Erstes wird die magische Summe errechnet. Die Eintragung in die Zelle 1 erfolgt erst bei Aufforderung dazu.
Variante 4
Die Variante 4 ist die Variante 3 mit einer einfachen Veränderung. Wenn man schon die Zellenzahlen einzeln berechnen muss, kann man das auch ohne Einsicht auf das Quadrat vornehmen und die Eintragung einem Gast übertragen. Der Akteur kann Abseits des Quadrates mit oder ohne Augenbinde die Zellenzahlen für die geforderte Zelle berechnen und zur Eintragung nennen.
Vorgabe einer magischen Summe
Bei einer Vorgabe der magischen Summe erfolgt die Berechnung in umgekehrter Reihenfolge wie die Berechnung bei Vorgabe einer Zellenzahl.
Dabei treten jedoch einige Probleme auf, die vorher genannt und gelöst werden sollten.
Ein Rest wird im Topquadrat den Zellen 13 bis 16 zugerechnet. Das sind beim 8er Quadrat die Quattros 13 bis 16. Da die Quattros 2*2=4 Zellen haben, befinden sich in jeder Reihe 2 davon. Daraus ergibt sich, dass der Rest den 4 Zellen nur zur Hälfte zugeschlagen werden kann. Der Rest muss folglich durch 2 teilbar sein und weiter, die magische Summe muss eine gerade Zahl sein. Mag schlägt vor, wie im 6er Quadrat beschrieben, um eine 2-stellige Primzahl zu bitten, um die die Vorgabe erhöht wird.
Bei der Erhöhung der Zahlen der Quattros 13 bis 16 um den Rest, kann es zu doppelten Zahlen kommen. Der Grund ist, dass die größten Zahlen der Quattros 1 bis 12 größer sind als die kleinste Zahl 13, der der Rest zugerechnet wird. Die größte Zahl der Quattros, denen der Rest nicht zugeschlagen wird, ist 12+3*16=60, die damit um 60-13=47 größer ist, als die kleinste Zahl 13, die um den Rest erhöht wird.
Doppelte Zahlen werden ausgeschlossen, wenn der halbe Rest größer als 47 ist. Der Gesamtrest muss 47*2=94 rd. 100 betragen.
Um das zu sichern, wird nicht nur die magische Summe von der Vorgabe abgezogen, sondern zusätzlich 100, zusammen 360, oder rd. 400.
Durch die Erhöhung nicht aller Zahlen um den Rest, ist das Quadrat, wie auch das Topquadrat, nicht mehr pandiagonal. Dadurch kann die Variante 2, wie bei der Vorgabe einer Zellenzahl, nicht auf die Quadratbildung bei einer Summenvorgabe übernommen werden. Das Basisquadrat kann nicht durch Versetzen von Zeilen und/oder Spalten verändert werden und auch kein anderes Quattro als 1. im Basisquadrat eingeordnet werden.
Die Probleme sind aus der Welt und die Quadratbildung mit einer vorgegebenen Summe kann erfolgen.
Die Vorgabe soll 746 sein und wird über das Quadrat geschrieben.
Nun müssen der Summand und der halbe Rest berechnet werden.
Von der Vorgabe wird 400 abgezogen und von der verbleibenden Summe 746-400=346 der Summand ermittelt. Dieser sollte eine durch 80 teilbare Zahl sein, damit ein Summand in Zehnergröße entsteht, mit dem besser gerechnet werden kann. Es bietet sich die Zahl 320 an. Der Summand wird dann 320/8=40.
Ausgehend vom Summanden wird der Rest und dessen Hälfte berechnet.
Von der Vorgabe 746 wird die magische Summe 260 und das 8fache des Summanden, das ist 320 und zusammen 260+320=580 abgezogen.
Das Ergebnis ist 746-580=166 als Rest und 166/2=83 der Endrest um den die Zahlen der Quattros 13 bis 16 zusätzlich zu erhöhen sind.
Der Endrest ist mit 83 größer als der notwendige Mindestwert von 50 und damit in Ordnung.
Die Quadratbildung kann erfolgen. Alle Zahlen des Basisquadrates werden, wie bei der Vorgabe einer Zellenzahl, um den Summanden 40 erhöht. Den Zahlen der Quattros 13 bis 16 wird jeweils der Endrest 83 zusätzlich zugerechnet.
Das fertige Quadrat ist das folgende.
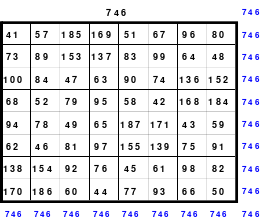
Das Quadrat ist magisch. Alle Reihen haben die Summe 746 entsprechend der Vorgabe. Keine Zahl ist doppelt vorhanden. Alle Zahlen sind gut verteilt, eine Regel ist nicht zu erkennen.
Da die Berechnung des Quadrates die gleiche ist, wie bei der Vorgabe einer Zellenzahl können auch die dort vorgestellten Varianten eingesetzt werden. Das trifft allerdings nicht auf die Variante 2 zu. Der Grund ist nicht nur die aufgehobene Pandiagonalität, sondern auch die Unveränderlichkeit des Summanden.
Die Variante 4 stellt den Höhepunkt mit einem guten Showwert dar und dürfte der Attraktivität der Darbietung in “Klein gegen Groß” in nichts nachstehen
Eine Nachbetrachtung
Die beschriebene Lösung ist wirklich fantastisch. Neben einer einfachen Berechnung muss hervorgehoben werden, dass praktisch jede Zelle des 8er Quadrates unabhängig von vorhergegangenen Zellen berechnet werden kann. Durch diese Form wird eine Falschberechnung, die eigentlich unzulässig ist, nicht auf folgende Zellenzahlen übertragen. Auch ist eine Fehlerbeseitigung problemlos möglich.
Größere Vorgaben sollten nicht zum Einsatz kommen, auch wenn die erhöhten Anforderungen problemlos gelöst werden können. 3- und 4-stellige Vorgaben führen zu einem ungünstigeren Zahlenbild. Wer trotzdem größere Vorgaben anstrebt, der müsste dann die Zahlen zusätzlich durch Multiplikation mit Schlüsselzahlen bilden.
Die Bestimmung jeder einzelnen Zelle und deren Berechnung, unabhängig von anderen Zellenzahlen, eröffnen interessante Möglichkeiten zu einer Qualitätsverbesserung der Vorführung, falls es einmal zu einer solchen kommen sollte.
Dazu hat Mag Varianten vorgeschlagen. Weitere sind möglich wie z.B. folgende:
Die Vorführung erfolgt durch ein Rechenkünstler-Duo, indem 2 Akteure im Wechsel die Zahlen ansagen. (Dadurch wird Zeit gewonnen bzw. die Vorführung geht flotter von der Hand.)
6.8. Quadrat der 9. Ordnung
6.8.1. Das rationelle 9er Quadrat
Gleich vorweg, ein 9er Quadrat ist nicht für Vorführungen geeignet. Es ist einfach zu groß. Natürlich könnte man mit Hilfe der Technik, zum Beispiel einen Beamer das Problem lösen, aber nur halb, denn die Größe erfordert einen höheren Zeitaufwand der nicht zu empfehlen ist. So ist das 9er Quadrat bereits um 65 % größer als das 7er und gegenüber dem Lo Shu Quadrat sogar um 800 %.
Wenn Mag trotzdem ein 9er Quadrat in das Hexen 1x1 aufnimmt, dann nur um zu zeigen, dass die rationelle Methode der Quadratbildung auch bei Triquadraten anwendbar ist. Allerdings bestehen dabei einige Schwierigkeiten mit den Vorgaben.
Diese Schwierigkeiten sind:
Triquadrate sind nicht homogen. Damit ist die Einordnung eines Restes nur sehr schwer zu realisieren. Folglich muss die Vorgabe einer magischen Summe durch die Ordnungszahl (im Beispiel 9) teilbar sein, was bei einer freien Wahl der MS unwahrscheinlich ist.
Die Vorgabe einer Zellenzahl muss mit der Ordnungszahl (z.B. 9) multipliziert werden um die magische Summe zu erhalten. Die Lösung, die Vorgabe durch gedankliches anhängen einer Null mit 10 zu multiplizieren und von dieser Zahl die Vorgabe abziehen, ist nur schwer fehlerfrei zu realisieren, zumal das Anschreiben der MS von links nach rechts erfolgen sollte.
Triquadrate sind nicht pandiagonal, weshalb die Vorgabe einer Anfangszelle nicht möglich ist.
Die Lösung
Eine allgemein gültige Lösung für die Triquadrate konnte nicht gefunden werden. Sie muss für die gewählte Größe jedes Mal erarbeitet werden.
Mag wird deshalb nur auf das von ihm gewählte 9er Triquadrat eingehen.
Zu 1.:
Hier sollte der Trick mit der Bildung von Zahlen mit den Ziffern von 1 bis 9 zur Anwendung kommen. Die Addition der Zahlen von 1 bis 9 ergibt die durch 9 teilbare Zahl 45. Dazu lässt man eine 4-stellige, 3-stellige und eine 2-stellige Zahl bilden, wobei jede Ziffer nur einmal eingesetzt werden darf. Dabei können die Ziffern beliebig eingeordnet werden.
(Zur Vermeidung eines wiederholten Einsatzes einer Ziffer sind diese nach Anwendung jeweils zu streichen.)
Die Addition der 3 Zahlen ist durch 9 teilbar. Die 4-stellige Zahl sollte dabei eine aus dem oberen Bereich (möglichst >4000) sein. Ist das nicht der Fall, so lässt man auch die 2. Zahl als 4-stellige bilden. Die Zahlen 1 bis 9 könnten dabei als Lo Shu Quadrat angeboten werden. (Das macht die Sache noch etwas interessanter.)
Zu 2.:
Auf die Vorgabe einer Zahl für die mittlere Zelle sollte verzichtet werden. Wer nicht darauf verzichten möchte, dem empfiehlt Mag die oben genannte Berechnung anzuwenden. Notfalls mit Anschreiben der MS von rechts nach links.
Zusammenfassend bleibt praktisch nur die Bildung einer magischen Summe aus Zahlen, die alle Ziffern 1 bis 9 enthalten übrig.
Mag wird ein Beispiel zur Bildung eines 9er Triquadrates zeigen, dass einer vorgegebenen magischen Summe entspricht.
Das folgende Quadrat der 9. Ordnung ist ein gesprungenes Triquadrat. Die Zelle 41 wurde durch Verschiebung von Zeilen und Spalten in der Mitte eingeordnet.
Nach den Regeln aus den 5er und 7er Primquadraten wurden die Starterzellen ermittelt und farblich dargestellt. Es sind die Zellen 41, 1 und 81, sowie die Zellen 10, 19. 28, 72, 63 und 54. Die Aufzählung entspricht der Reihenfolge der Bildung.
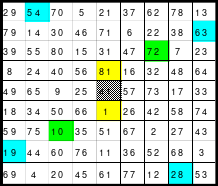
Drei Personen bildeten aus den Ziffern 1 bis 9 die Zahlen 6129, 543 und 87 deren Summe 6759 ist und als magische Summe über das Quadrat geschrieben wurde.
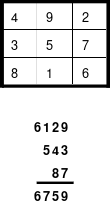
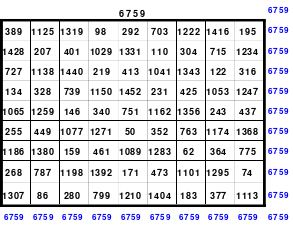
Es wurden folgende Berechnungen vorgenommen: (Die Kenntnisse aus den 5er und 7er Quadraten werden vorausgesetzt!)
MS/O = 6759/9 = 751 für Zelle 41
DZ1 gewählt 701 (711 wäre wegen der Zahlen 50, 751 und 1452 besser)
Zahl für Zelle 1 = 751-701 = 50
Zahl für Zelle 81 = 751+701 = 1452
DZ2 = DZ1/(O/2) =~ 701/5 =~ 140 gewählt 109
Startzahl für Zelle 10 = 50+109 = 159
19 = 159+109 = 268
28 = 268+109 = 377
72 = 1452-102 = 1343
63 = 1343-109 = 1234
54 = 1234-109 = 1125
SZ = DZ2/O = 109/9 = 12
Ausgehend von den Startzahlen wurden die auf- und absteigenden Zahlenreihen durch stetige Addition bzw. Subtraktion der Schlüsselzahl 12 berechnet.
Das fertige Quadrat ist ein magisches. Alle Spalten, Zeilen und die beiden Diagonalen haben alle die richtige Summe der Vorgabe von 6759.
Die Zahlen sind breit gestreut und zeigen keine Auffälligkeiten.
Das Quadrat ist jedoch nicht pandiagonal. Es können aber jeweils 3 Spalten und/oder Zeilen versetzt werden, wobei das Quadrat ein magisches bleibt.
6.8.2. Fantastisch * *
Bei diesem Experiment kommt ein Quadrat der 9. Ordnung zum Einsatz. Mag lässt sich eine 2-stellige Zahl größer 50 nennen. Es wird 83 genannt. Diese setzt er in die 1. Zelle ein. Nach einem kurzen Moment schreibt er über das Quadrat die Zahl 837. Anschließend füllt er Zeile um Zeile alle Zellen mit Zahlen aus. Das fertige Quadrat ist ein magisches mit der magischen Summe von 837, wie er es anfangs über das Quadrat geschrieben hat.
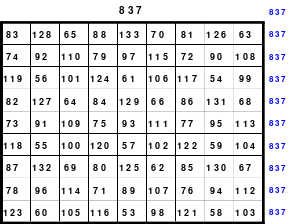
Mag hat das Ergebnis als erstes erläutert, um Ihnen Zeit zu lassen, eventuelle Regeln über den Quadrataufbau zu erkennen. Sie müssen zugeben, dass dies kaum möglich ist.
Bei diesem Experiment handelt es sich wie beim 8er Quadrat um ein Fusionsquadrat. Es entstand aus 9 Wechselquadraten des Lo-Shu-Quadrates, die in das Lo-Su-Quadrat eingesetzt wurden.
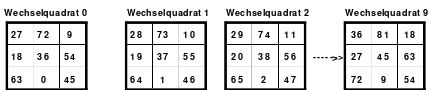
Am Wechselquadrat 1 ist zu erkennen, dass jede folgende Zellenzahl um 9 größer ist, was der Anzahl der Wechselquadrate entspricht. In jedem folgenden Wechselquadrat sind die Zellenzahlen um 1 größer als im vorangegangenen. Daraus abgeleitet ergibt sich ein Wechselquadrat 0, dass um 1 kleinere Zellenzahlen als Wechselquadrat 1 hat.
Diese Erkenntnisse sind ausreichend um ein Basisquadrat der 9. Ordnung zu bilden und vor allem um jede Zelle zu bestimmen und zu berechnen können.
Im folgendem Basisquadrat sind die 9 Wechselquadrate, auch Teilquadrate genannt, in das Lo-Shu-Quadrat eingeordnet. Da das Lo-Shu-Quadrat ein magisches ist, entsteht so ebenfalls ein magisches Quadrat, wobei kein Wenden oder dergleichen notwendig wird. Alle Zahlen von 1 bis 81 sind lückenlos vorhanden. Keine Zahl ist doppelt. Die magische Summe ist 369 (370-1). Wie das Lo-Shu-Quadrat, ist dieses 9er Basisquadrat auch nicht pandiagonal.
Um den logischen Aufbau des Basisquadrat zu erkennen, wurden die 3er Quadrate mittels Trennlinien abgegrenzt. Diese Abgrenzungen dürfen im Original natürlich nicht verwendet werden. Das trifft auch auf die Spalten- und Zeilenzahlen zu, es sei denn, diese werden zur Benennung von Zellen benötigt.
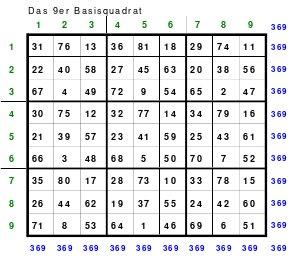
Wird die Zelle in Spalte 6 und Zeile 5 gewählt, so wissen Sie, dass es sich um die Zelle 7 im Quadrat 5 handelt. Dazu ist die gute Kenntnis des Systems erforderlich, was aber als unschwer eingeschätzt werden kann. Die Zellenzahl kann berechnet werden durch 5 (Nummer des Wechselquadrates) + 7 (Zellenzahl)-1) *9 (Ordnungszahl) = 5+54=59.
Die Lösung
wird am Beispiel der Vorgabe 83 erklärt. Die Zahl 31 in Zelle 1/1 muss man sich gut merken. Wird die Vorgabe genannt, wird diese in die Zelle 1/1 eingetragen. Die Vorgabe ist um 83-31=52 größer. Diese 52 muss allen Zellen zugeschlagen werden. Die magische Summe wird damit um 9*52=520-52=468 größer und das ist 369+468=837, die über das Quadrat geschrieben wird.
Nun könnte jede in der Zeile folgende Zelle ermittelt und berechnet werden. Mag geht aber einen rationelleren Weg.
Die nächste Zelle ist im Lo-Shu-Shu-Quadrat die Zelle 9. Diese ist um 5 größer als die Startzelle 4. Deshalb erhöht er die Zahl in Zelle 1 um 5*9=45. Das ist 83+45=128.
Die nächste Zelle ist die Zelle 2, die um 2 kleiner als Zelle 4 ist. Deshalb wird von 83 2*9=18 abgezogen. Das ist 65.
Nun folgen die Zellen des 9. Wechselquadrates und hier sind die Zahlen um 9-4=5 größer als die Zahlen im Wechselquadrat 4. Damit werden die 3 folgenden Zahlen 83+5=88, 128+5=133 und 65+5=70 groß.
Genau so wird mit Wechselquadrat 2 verfahren. 2 ist um 2 kleiner als 4, weshalb die nächsten 3 Zahlen die Größe 83-2=81, 128-2=126 und 65-2=63 haben. Natürlich kann auch vom Wechselquadrat 9 aus berechnet werden, wo die Differenz -7 ist. Das Ergebnis ist das Gleiche.
Jetzt geht es in die nächste Zeile. Hier ist die 1. Zelle eine Zelle 3, die um 1 kleiner als Zelle 4, die Startzelle, ist. Deshalb wird von der Vorgabe 83 1mal 9 abgezogen und das Ergebnis 83-9=74 in diese Zelle eingetragen. Von dort geht es zur Zelle 5, in die eine 5-3=2*9=18 größere Zahl, das ist 74+18=92 kommt. Die 3. Zahl in dieser Zeile wird dann 7-5=2*9=18 größer, das ist 92+18=110. Die nächsten Zahlen sind wieder 5 größer, das sind die Zahlen 79, 97 und 115. Dann folgen die um 2 kleineren Zahl, verglichen mit den Zahlen im 4. Wechselquadrat. Das sind die Zahlen 81, 126und 108.
So geht es weiter, bis in allen Zellen der oberen 3 Wechselquadrate eine Zahl steht.
Für die folgenden Wechselquadrate kann die Berechnung wie bei den Wechselquadraten 9 und 2 vorgenommen werden. Alle Zahlen anderer Wechselquadrate sind um +/- der Differenz zwischen diesen größer oder kleiner. Das wird sehr deutlich im Vergleich der Teilquadrate 3 und 4. Im Teilquadrat 3 sind alle Zahlen um 1 kleiner als im Teilquadrat 4, oder um 1 größer als im Teilquadrat 2.
Mag hofft, dass Sie diese rationelle Berechnung verstanden haben. Sie können sich durch die Berechnung aller weiterenn Zellenzahlen von der Richtigkeit überzeugen.
Es ist jedoch ratsam ab und zu eine richtige Berechnung vorzunehmen, um so durch Vergleich die Richtigkeit zu bestätigen.
Die Berechnung ist total einfach. Dafür sind die Anforderungen an das Denken im System der Quadratgestaltung höher, aber ohne Probleme beherrschbar.
Variante 2
Hier werden die Zahlen nicht zeilenweise eingeschrieben, sondern in einer scheinbaren Unregelmäßigkeit.
Dazu wird nacheinander für jedes Teilquadrat eine Zelle und deren Zahl berechnet und eingetragen. Die Reihenfolge der Quadrate und der Zellen sollten nicht gleichmäßig sein, um so keine Regel erkennen zu lassen.
Von diesen Zellen aus, können dann die anderen Zellen in ihrer Folge durch +/-9 ermittelt werden. Dabei soll nicht ein Teilquadrat nach dem anderen fertiggestellt werden, sondern in einer Unregelmäßigkeit immer eine beliebige, noch leere Zelle.
Dazu ein Beispiel. Nach Eintrag der Vorgabe und der magischen Summe werden in jedes Teilquadrat und in einer beliebigen Zelle eine Zahl berechnet und eingesetzt.
Das könnte wie folgt geschehen:
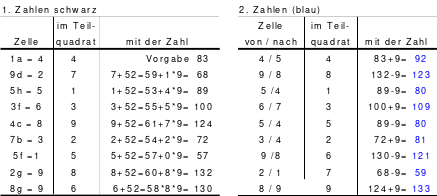
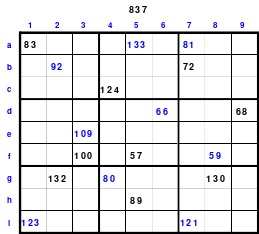
So wird weiter verfahren bis das Quadrat fertig ist.
Variante 3
Nach der Eintragung der Vorgabe und der magischen Summe bestimmen die Gäste in welche Zellen die nächsten Zahlen geschrieben werden sollen.
Das bedeutet, dass der Akteur jede Zelle ermitteln und jede Zahl berechnen muss.
Variante 4
Der Akteur befindet sich Abseits, mit oder ohne Augenbinde und nennt einem Helfer die Zahlen, die in die Zellen einzutragen sind.
Die Eintragungen können zeilenweise wie in Variante 1 oder in von Gästen bestimmten Zellen, entsprechend der Variante 3 erfolgen.
Zum besseren Verständnis sind die Zeilen nicht mit Buchstaben, sondern ebenfalls mit Zahlen zu versehen.
Vorgabe einer magischen Summe
Als erstes muss auf ein Problem hingewiesen werden. Das Lo-Shu-Quadrat ist nicht homogen, weshalb ein Rest keinem Block zugeordnet werden kann. Um das Problem zu lösen muss die Vorgabe der magischen Summe eine durch 9 teilbare Zahl sein. Sie muss eine Zahl größer als die magische Summe des Basisquadrates mit 369 sein.
Mag hat dazu bereits Lösungen aufgezeigt, wiederholt aber nochmals die Variante mit den Ziffern von 1 bis 9. Es werden von den Gästen 3-, 2- auch 1-stellige Zahlen gebildet, wobei jede Ziffer nur 1mal eingesetzt werden darf. Die Summe dieser Zahlen ist die magische Summe, wenn die Quersumme oder die Summe der noch nicht eingesetzten Ziffern durch 9 teilbar ist.
Mag bittet als erstes um eine 3-stellige Zahl. Ist diese größer 369 und deren Quersumme durch 9 teilbar, kann diese als magische Summe eingesetzt werden. Ist sie größer 369, aber deren Quersumme nicht durch 9 teilbar, bittet Mag um weitere 2-stellige Zahlen, bis die Quersumme aller eingesetzten Ziffern oder die Summe der noch nicht verwendeten Ziffern durch 9 teilbar ist.
Sollte die 3-stellige Zahl kleiner 369 sein, wird um eine weitere 3-stellige Zahl gebeten. Anhand der der noch nicht eingesetzten 3 Ziffern ist zu erkennen, ob die Summe durch 9 teilbar ist. Wenn nicht, werden weitere Zahlen erbeten, notfalls bis alle Ziffern eingesetzt sind. Ist die magische Summe gefunden, wird diese über das Quadrat geschrieben und die weiteren Berechnungen vorgenommen.
Von der Vorgabe wird die magische Summe des Basisquadrates von 369 abgezogen und der Rest durch 9 dividiert und der Summand ist gefunden. Um diesen sind alle Zahlen des Basisquadrates zu erhöhen. Das erfolgt in der gleichen Art und Weise wie bei der Vorgabe einer Zellenzahl. Auch die dort genannten Varianten sind möglich.
Im Beispiel ist die magische Summe 792, deren Quersumme 18 ist durch 9 teilbar. Nach Abzug von 369 verbleibt ein Rest von 792-370+1=423. Durch 9 dividiert ergibt 47 als Summand. Die Zahl in Zelle 1/1 wird als Beispiel 31+47=78 groß.
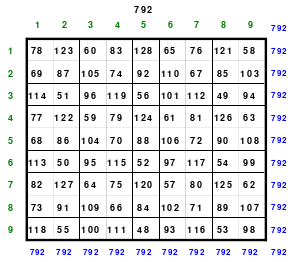
Eine Nachbetrachtung
Sie werden sicherlich auch der Meinung sein, dass die gefundene Lösung einfach “Fantastisch” ist. Die Rechenleistungen sind nicht nennenswert und die Beherrschung des Systems des Quadrataufbaues und die Bestimmung jeder einzelnen Zelle eine machbare Angelegenheit. Bedauerlich ist, dass ein Quadrat der 9. Ordnung zu groß für eine Vorführung im größeren Rahmen ist. Auch ein kleiner Kreis Interessierter wird selten zu finden sein.
Der wirkliche Fan wird sich sicherlich trotzdem damit beschäftigen und vielleicht den Wunsch haben, größere Vorgaben einzusetzen, was möglich, aber schwerer ist. Denn dann muss die Berechnung nach der Multimethode vorgenommen werden.
Selbst eine kleinere Erhöhung der Vorgaben, z. B. auf 3-stellige Zahlenvorgaben kleiner 300, oder 4-stellige Summenvorgaben kleiner 2000 sind nicht günstig. Sie können zu einem schlechten Zahlenbild führen. Der Grund ist die lückenlose Zahlenreihe der Zahlen von 1 bis 81. Würde z.B. eine Zahlenvorgabe von 247 gemacht, würde der Summand 247-31=216 groß und alle Zahlen dann 217 bis 297, nur Zahlen der 200er Reihe sein.
Wenn Mag seine Ausführungen hier beendet, ist noch nicht Alles betrachtet und bietet für den Fan interessante Fragen zur Klärung. Das könnte die Frage nach der Gestaltung der nächsten Größe, einem 12er Fusionsquadrat sein. Ist die Variante 3er Wechselquadrate in das Topquadrat einzuordnen günstiger als umgekehrt? Ist eine der Varianten evtl. auch pandiagonal wie das 8er? Oder wenigstens die Verschiebung von jeweils 3 Reihen und/oder Spalten möglich?
Aber auch das 8er - und 9er Quadrat bieten sicherlich Stoff für Überlegungen. Das könnte die Frage nach einer tauglichen Lösung sein, die Summenvorgaben nicht auf 2 oder 9 teilbare zu begrenzen
6.9. Nachtrag
6.9.1. Und 10 ist keins * *
Wie heißt es doch in Goethes Hexeneinmaleins? “Und 10 ist keins.”
Daran hat sich Mag auch gehalten und mit dem Quadrat der 9. Ordnung das Hexen 1x1 abgeschlossen.
Seine Meinung, dass zu fast allen Quadrattypen eine Lösung im Hexen 1x1 erläutert wurde, musste er im Nachhinein korrigieren. Eine größere Gruppe von Quadrattypen sind die einfach geraden Quadrate wie das Quadrat der 6. Ordnung. Die Lösung zum 6er Quadrat im Hexen 1x1 ist jedoch nicht auf andere einfach gerade Quadrate übertragbar. Die Lösung setzte beim 6er Quadrat das Wissen der Zahleneinordnung im Lo-Shu-Quadrat voraus, was aber bei größeren Quadraten wie das 10er, 14er usw. kaum zu machen ist.
Mag hat sich deshalb entschieden, auch für ein Quadrat der 10. Ordnung einen Lösungsweg auszuarbeiten der für weitere einfachgerade Quadrate anwendbar ist. Auch hier gilt, dass eine Vorführung höchstens am Stammtisch von Interessierten möglich ist, obwohl der gefundene Lösungsweg unschwer erlernt werden kann.
Wenn Mag diesem Experiment 2 Sterne zuerkannt hat, erfolgt dies wegen der Größe eines 10er Quadrates und der erhöhten Anforderungen an das Systemdenken. Die Rechenleistungen sind nicht erheblich, aber merken muss man sich Einiges. Das Schwierigste dürfte die abgeforderte hohe Konzentration sein, die insbesondere beim Einsetzen der 2. bis 5. Zahlen der Blöcke zwingend erforderlich ist.
Die Lösung baut im Wesentlichen auf Komponenten auf, die in den vorangegangenen Experimenten beschrieben wurden. Mag wird deshalb auf eine umfassende Erläuterung verzichten. dafür das Wesentliche jedoch ausführlich erklären.
Das 10er Quadrat im Hexen 1x1
Der Lösungsweg:
Grundlage der Berechnungen ist eine leicht erweiterte Matrix für Korrekturquadrate der 5. Ordnung, z. B. dem gewählten Pentaquadrat, denn das 10er Quadrat besteht aus 4 von 5 Korrekturquadraten der 5. Ordnung.
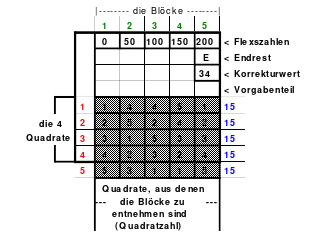
Die Erweiterungen sind:
1. Flexzahlen:
Diese wurden in einer Größe gewählt, die doppelte Zahlen ausschließen und ein leichtes Rechnen erlauben. Sie ersetzen praktisch die Berechnungen der 1. Zahlen für die Blöcke nach der Formel Zn=(Bn-1) *A*O*SZ.
Darin bedeuten: Zn = 1. Zahl im Block Bn
Bn = Block für den die erste Zahl berechnet werden soll
A = Anzahl der zu bildenden Korrekturquadrate (in diesem Fall 5)
O = Ordnungszahl der Teilquadrate (in diesem Fall 5)
SZ = Schlüsselzahl (in den aufgeführten Experimenten 1)
Qn = Quadrat aus dem der Block zu entnehmen ist. (wird der Matrix entnommen)
Die Berechnung der Zahlen für die 1. Zellen der Blöcke erfolgt jedoch viel einfacher durch Addition von Flexzahl plus Quadratzahl. Zum Beispiel für den 3. Block im 4. Quadrat = 100+3=103. Nach der genannten Formel würde, dass sein: Zn= (3-1) *5*5*1+4=55
Die Flexzahl hätte demzufolge auch 60 sein können. Die Reserve von 45 kann für eventuelle Manipulationen genutzt werden.
2. Endrest:
Ein Endrest kann bei Vorgabe der magischen Summe entstehen. Er wird den letzten, den 5er Blöcken, zugeschlagen und wird in jeder Reihe des 10er Quadrates 2mal wirksam, weshalb auch hier die magische Summe eine gerade Zahl sein muss.
3. Korrekturwert:
Der Korrekturwert wird der magischen Summe zugerechnet, damit diese für die Berechnungen leichter zu handhaben ist. Im konkreten Fall 34, wodurch die magische Summe von 1130 um 2*34 auf 1198 erhöht wird, was auch 1200-2 ist.
4. Vorgabenteil:
Der Vorgabenteil ist die Differenz zwischen Vorgabe und Zellenzahl in die die Vorgabe eingesetzt wird. Wird die Vorgabe, z. B. 135, in die erste Zelle von Block 3 im Quadrat 1 eingesetzt, in der sich die Zahl 104 normalerweise befindet, so ist der Vorgabenteil 135-104=31.
Die nachfolgende Abbildung zeigt die Einordnung der Pentaquadrate in das Gesamtquadrat der 10. Ordnung.
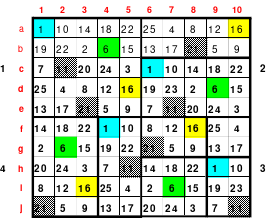
Das Quadrat 1 ist das unveränderte Pentaquadrat.
Beim Quadrat 2 wurden die unteren 2 Zeilen nach oben versetzt.
Beim Quadrat 4 wurden die 2 vorderen Spalten nach hinten verschoben und
im Quadrat 3 wurden Umgestaltungen entsprechend Quadrat 2 und 4 vorgenommen.
Die Folge dieser Einordnung ist, dass die Zellen für die 1. Zahlen der Blöcke mit einem Sondersprung erreicht werden. Dieser geht jeweils 5 Felder zum nächsten Quadrat und dann im rechten Winkel 3 Felder nach außen. Ist das nicht möglich muss 2 Felder nach innen gegangen werden. Dadurch wird die Eintragung der Zahlen nicht immer in gleichmäßiger und auffälliger quadratischer Ordnung vorgenommen.
Auch zeigt die Abbildung die Regel zum Finden der 1. Zelle des folgenden Blockes. Zu diesem gelangt man durch einen Linkssprung (2 Felder nach links und 1 Feld nach unten), sowie die Regel zur Findung der 1. Zelle im vorherigen Block durch einen Returnsprung (2 Felder nach rechts und 1 Feld nach oben).
Das Ausgangsquadrat
Nach den genannten Regeln wurde das Ausgangsquadrat gebildet.
Links ist die auf das notwendigste reduzierte Matrix und rechts das Ausgangsquadrat.
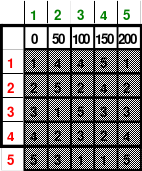
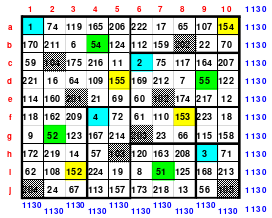
Die ersten Blöcke in den 4 Quadraten sind blau hinterlegt, grün die zweiten, rot die dritten, gelb die vierten und grau die fünften Blöcke. Die Zahlengröße ergibt sich aus Flexzahl plus Quadratzahl. Die magische Summe ist 1130.
Der Aufbau des Ausgangsquadrates ist leicht nachvollziehbar. Dazu eine kurze Erläuterung zu den zweiten Blöcken in den grünen Zellen.
Von der Zelle 1a gelangt man mit einem Linkssprung zur Zelle 4b in die die erste Zahl des zweiten Blockes eingesetzt wird. Das ist 50+4=54 für das 1. Quadrat. Nach einem Sondersprung kommt man zur Zelle 9d im 2. Quadrat, in die 50+5=55 kommt. Nach einen weiteren Sondersprung kommt man zur Zelle 7i im 3. Quadrat. Hier wird 50+1=51 eingesetzt. So geht es weiter bis mit den 4. Sondersprung die Ausgangszelle 4b wieder erreicht wird. Von hier aus geht es mit Linkssprung zur Zelle 2c, in die die erste Zahl des 3 Blockes 100+4=104 geschrieben wird. So werden alle 1. Zahlen der 20 Blöcke gefunden und die entsprechende Zahl eingesetzt. Von diesen ausgehend werden in Rechtssprüngen
(2 nach rechts 1 nach unten) die weiteren 4 Zellen der Blöcke gefunden. In diese werden jeweils um 5 erhöhte Zahlen eingesetzt.
Wichtig ist, dass dabei das entsprechende Quadrat nicht verlassen wird! So darf nicht von Zelle 4b zur Zelle 6c gesprungen werden, sondern zur Zelle 1c, in die die Zahl 54+5=59 kommt.
Das so entstandene Quadrat ist magisch, aber nicht pandiagonal.
Die magische Summe ist 1130. Sie ergibt sich ausfolgender Berechnung:
Das Basisquadrat
Man muss nicht, aber kann die magische Summe so verändern, dass ein leichteres Rechnen erreicht wird. Im vorliegenden Fall wurde die magische Summe auf 1198, das ist auch 1200-2 verändert. Dazu wurde ein Korrekturwert von 34 eingesetzt, der in jeder Reihe des Basisquadrates 2mal wirksam wird und dadurch die magische Summe um 68 erhöht. Das so veränderte Quadrat ist das Basisquadrat und ist Grundlage für die Berechnung von Quadraten bei Vorgabe einer Zellenzahl oder der magischen Summe.
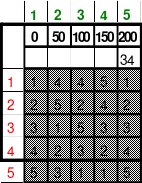
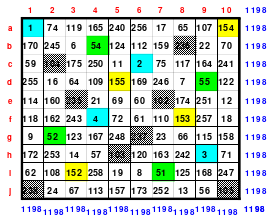
Die eingesetzten Pentaquadrate bleiben trotz der Umbildung zu Korrekturquadraten, Verschiebung von Zeilen und/oder Spalten und der Zuschläge (Flexzahlen, Endrest, Korrekturwert und Vorgabenteil) pandiagonal und homogen. Das bedeutet auch, dass jede Zelle innerhalb des ersten Quadrates jede Position einnehmen kann, so auch die Zelle 1a.
Die Schlussfolgerung ist, dass auch jede 1. Zahl der 5 Blöcke diese Zelle einnehmen kann und damit die Vorgabe grundsätzlich in die Zelle 1a eingesetzt werden sollte. An den Sprüngen ändert sich nichts, auch nicht beim Übergang von Block 5 zu Block 1. Dieser ist gleich den Sprüngen wie zu den folgenden Blöcken.
Diese Aussage trifft nur auf das Quadrat 1 zu. Ein Start aus einem anderen Quadrat ist nicht möglich, da sich der Sondersprung verändern kann.
Beim nachfolgenden Quadrat wurde die 1. Zahl des 5ten Blocks des 1. Quadrates, die 235, in die Zelle 1a eingesetzt. Von dort aus erfolgte der Aufbau des Quadrates bei Anwendung unveränderter Sprünge.
Das Quadrat ist magisch und mit der richtigen magischen Summe von 1198 geblieben.
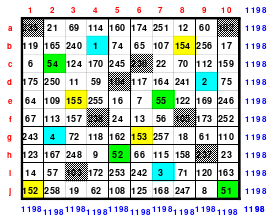
Die schwerste Aufgabe dürfte die richtige Einordnung der 2. bis 5. Zahlen der Blöcke sein. Grundsätzlich müssen die Sprünge zu den 4 restlichen Zahlen der Blöcke innerhalb der Teilquadrate erfolgen. Das setzt voraus, dass die Begrenzungen der Quadrate beachtet werden müssen. Das kann schwierig werden, da ja die in den Beispielen gezeigten Trennungen normalerweise nicht vorhanden sein dürfen. Um wenigstens einen Anhaltspunkt zu haben, sollte die Mitte möglichst unauffällig markiert werden.
Bevor es zur praktischen Anwendung der Erkenntnisse kommt, erachtet Mag ein paar mathematische Betrachtungen zur Flexibilität des Basisquadrates als sinnvoll.
Um größere Vorgaben zuzulassen sind 4 Wege möglich. So können 1. nur die Flexzahlen oder 2. alle Zahlen der Matrix mit einer Schlüsselzahl vergrößert werden. Eine solche Maßnahme sollte aber gut überlegt werden. Auch auf die 3. Möglichkeit sollte verzichtet werden. Bei dieser werden größere Vorgaben zugelassen ohne eine Veränderung der Matrix vorzunehmen. Die Folge sind unter Anderem bis zu 3-stellige Vorgabenteile und große Zahlenlücken zwischen den Blöcken. Als 4. können 3-stellige Vorgabenteile zugelassen werden, was ebenfalls keine gute Idee ist. Denn dann fehlen im Quadrat 1- und 2-stellige Zahlen und mit jedem Hunderter größer weitere 100. In fast allen Möglichkeiten kommt es zu einem schlechteren Zahlenbild und zu einer zusätzlichen Belastung durch das Merken weiterer Zahlen und höhere Rechenleistungen, was nicht notwendig ist.
Mag schätzt deshalb das vorgeschlagene Basisquadrat als eine günstige Lösung ein. Die Vorgaben für die Zellenzahlen sollten nicht größer 300 und die Vorgaben für die magischen Summen 4-stellig kleiner 2000 sein, was völlig ausreichend ist.
Als zweckmäßig erweist sich lediglich die im Rahmen der Reserve gerade noch mögliche Reduzierung der Flexzahlen auf die Werte 30 bis 120, aber nur bei Vorgaben der magischen Summe von kleiner 1200. Warum, erfahren Sie im Abschnitt “Vorgabe einer magischen Summe”.
Doch nun zu den praktischen Anwendungen des erworbenen Wissens.
Vorgabe einer Zellenzahl
Die Vorgabe sollte nicht größer 300 sein und wird in die Zelle 1a eingetragen. Im Beispiel ist die Vorgabe 187.
Danach wird festgelegt, welche 1. Zahl eines Blockes dieser Zelle zugeordnet werden muss, wenn der Vorgabenteil nicht größer als 2-stellig werden soll. Dazu wird vereinfacht geprüft welche Flexzahl von der Vorgabe abzuziehen ist. 200 kann von 187 nicht abgezogen werden, aber 150. Damit sind es die 4. Blöcke. Daraus ergibt sich, dass in der Zelle 1a normalerweise 150+5=155 stehe müsste. Das sind 187-155=32 mehr. Dies ist der Vorgabenteil um den alle Zahlen im Quadrat erhöht werden müssen.
Da es sich um ein Quadrat der 10. Ordnung handelt, muss der magischen Summe des Basisquadrates das 10-fache des Vorgabenteils zugeschlagen werden. Das ist 32*10+1200-2=1518 und wird sofort über das Quadrat geschrieben.
Denkbar ist auch der Einsatz der Vorgabe als 1. Zahl der 3. Blöcke. Dann wird der Vorgabenteil 187-104=83 und die magische Summe 83*10=830+1200=2030-2=2028 groß. Eine weitere Abstufung ergibt 3-stellige Vorgabenteile. So bei Einsatz als 1. Blöcke. Hier wird der Vorgabenteil 187-1=186 groß und die magische Summe 186*10=1860+1200=3060-2=3058.
Diese Berechnungen zeigen, dass bei Vorgaben der magischen Summe von rd. kleiner 2000, 2-stellige und bei Vorgaben größer 2000, 3-stellige Vorgabenteile entstehen.
Die genaue Abgrenzung ist 99*10+1200-2=2188 bzw. 199*10+1200-2=3188, letztere bei Vorgaben als magische Summe die einen Vorgabenteil kleiner 200 ergeben. Größere Werte werden nicht empfohlen, da dann die Zahlenstreuung ungünstig wird.
Bei Einsatz eines Korrekturwertes muss beachtet werden, dass dieser der 5ten Flexzahl zugerechnet werden muss. Im Beispiel ist das 200+34=234. Ist die Vorgabe kleiner, kann diese nicht den 5ten, sondern muss den 4ten Blöcken zugeordnet werden,
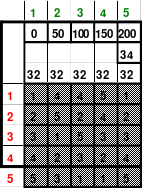
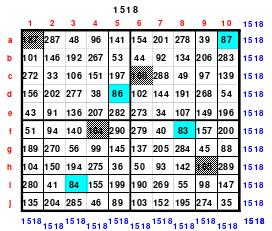
Die Entscheidung war, Einsatz der Vorgabe 187 in die Zelle 1a, als 1. Zahl der 4. Blöcke.
Von dort geht es im Sondersprung zur Zelle 6e im 2. Quadrat. Nach der Matrix ist die 1. Zahl des 4. Blockes im Quadrat 2 um 1 kleiner, also 186, die in die Zelle 6c kommt. Weiter mit Sondersprüngen zu den Zellen 9h und 4f im 3. und 4. Quadrat in die 185 und 184 einzusetzen sind. Von dort kommt man mit einem weiteren Sondersprung zurück zur Zelle 1a. (Siehe grüne Zellen)
Von dort gelangt man mit einem Linkssprung zur Zelle 4b, der 1. Zelle des 5. Blockes. Hier ist die Zahl 200+34+32+1=267 einzutragen. In die folgenden Quadrate werden die Zahlen im Gegensatz der 4. Blöcke immer um 1 kleinere Zahlen eingesetzt.
Nach einem weiteren Sprung zurück zur Zelle 4b, geht es im Linkssprung zur Zelle 2c in die 32+1=33 eingeschrieben wird. Die Zahlen in den folgenden Quadraten sind ebenfalls jeweils um 1 größer.
Für die 2. Blöcke ist die Zahlenfolge nicht gleichmäßig +1 oder -1, sondern entsprechend der Matrix +1, -4 und +1. Die Zahlen für die einzelnen Quadrate sind für das 1. Quadrat 50+32+4=86, 2. Quadrat 87, 3. Quadrat 83 und 4. Quadrat 84. (siehe blaue Zellen)
Die ersten Zahlen für die 3. Blöcke sind, ausgehend von der Zahl in der Zelle 3e im 1. Quadrat von 100+32+4=136 für die Quadrate 2, 3 und 4 folgende: -2=134, +3=137 und -2=135, wie es in der Matrix aufgeführt ist.
Mit einen weiteren Sondersprung gelangt man zurück zur Zelle 3e und mit einem Linkssprung zur Zelle 1a, in der sich die Zahl 187 befindet und damit anzeigt, dass alle 1. Zahlen der 20 Blöcke eingetragen sind.
Wichtig ist, dass alle Sprünge, außer den Sondersprüngen, nur innerhalb der 5er Quadrate erfolgen dürfen. Das bedeutet, dass der letztgenannte Linkssprung von Zelle 3e nicht zur Zelle 1f gelangt, sondern zur Zelle 1a. Diese Regel gilt auch für die Rechtssprünge bei der Eintragung für die noch leeren Zellen, was der nächste Schritt ist.
Ausgehend von den ersten Zahlen der 20 Blöcke, Mag nennt sie Startzahlen, werden die restlichen 4 Zahlen der Blöcke eingesetzt. Dazu werden nach Rechtssprüngen jeweils um 5 größere Zahlen in die Zellen geschrieben. Das wird am Beispiel der Startzahl 84 in der Zelle 3i beschrieben..
Von der Startzahl 84 in Zelle 3i wird im Rechtssprung zur Zelle 5j gegangen und die um 5 größere Zahl 89 eingetragen. Weiter mit Rechtssprung zur Zelle 2f (nicht zur Zelle 201!) in die 89+5=94 kommt. Weiter zur Zelle 4g mit der Zahl 99 und dann zur Zelle 1h (nicht zur Zelle 6h!) in die die Zahl 104 geschrieben wird. Mit einem weiteren Rechtssprung kommt man zur Zelle 3i zurück. Die dort vorhandene Zahl 84 signalisiert, dass der Block fertig ist und der nächste bearbeitet werden kann.
In der gleichen Art und Weise werden die restlichen Blöcke vervollständigt.
Das fertige Quadrat ist magisch mit der magischen Summe von 1518, wie sie anfangs über das Quadrat geschrieben wurde. Alle Zahlen kommen nur einmal vor, keine ist doppelt.
Ein Hinweis darauf, dass die 4 Quadrate der 5. Ordnung ebenfalls magisch und sogar pandiagonal sind, sollte unterlassen werden, weil es sonst zur Annahme kommt, dass ganz einfach nur 4 Quadrate wie bekannt erstellt und zusammengefügt wurden.
Die Nummerierung der Spalten und Kennzeichnung der Zeilen, wie auch die Summenangaben und die Unterteilung in 4 Quadrate dienen lediglich zum besseren Verständnis der Erläuterungen. Falls ein Gast Ihrer Quadratgestaltung zusehen sollte dürfen sie nicht vorhanden sein.
Das trifft auch auf die Matrix zu, die nur in Ihrem Gedächtnis existieren darf.
Bitte beachte Sie auch die weiteren Hinweise und Ratschläge in der Nachbetrachtung.
Vorgabe einer magischen Summe
Bei einer Vorgabe der magischen Summe erfolgt die gleiche Berechnung wie bei der Vorgabe einer Zellenzahl, nur dass die Berechnungen rückläufig ausgeführt werden. Allerdings treten dabei einige zusätzliche Besonderheiten auf, die jedoch kein Problem darstellen.
Als Vorgabe sollte eine 4-stellige Zahl kleiner 2000 erbeten werden. Größere Vorgaben sind möglich, haben allerdings 3-stellige Vorgabenteile und ein schlechteres Zahlenbild zur Folge.
Der Rechnungsablauf wird mit einer Vorgabe von 1734 erklärt.
Von der Vorgabe wird die magische Summe das Basisquadrates abgezogen und man erhält 1734-1200=534+2=536. Dieser Wert muss anteilig den Flexzahlen zugeschlagen werden. Da die Reihen im 10er Quadrat 10 Zahlen enthalten ist das 536/10=53 als Vorgabenteil und 6 als Rest. In jeder Reihe befinden sich jeweils Zahlen von zwei 5er Blöcken weshalb der Rest von 6 diesen zur Hälfte zugeschlagen werden muss. Der Endrest ist damit 6/2=3.
Aus rationellen Gründen wird als erstes die 1. Zahl der 1. Blöcke mit 53+1=54 berechnet und in die Zelle 1a eingesetzt. Als nächstes wird die 1. Zahl der 5er Blöcke mit 200+3+34+53+1=291 gebildet und in die Zelle 3e geschrieben. Diese Zelle erreicht man mit einem Returnsprung (2 rechts,1 nach oben).
Mit diesem kleinen Trick kann der Wert des Vorgabenteils vergessen werden. Man kann diesen ja jederzeit aus der Zelle 1a nach Abzug von 1 abrufen. Auch die Einordnung des Endrestes hat sich erledigt. Er wird automatisch in die restlichen Zellen der 5er Blöcke übernommen.
Die Berechnung der weiter 18 Startzahlen und deren Eintrag in die Zellen erfolgt wie bei der Vorgabe einer Zellenzahl. Das trifft auch auf die restlichen Zahlen der Blöcke zu.
Das fertige Quadrat ist magisch mit der einheitlichen Summe aller Reihen von 1734, was der Vorgabe entspricht und keine Zahl ist doppelt vorhanden.
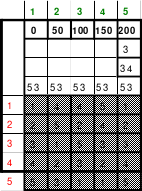
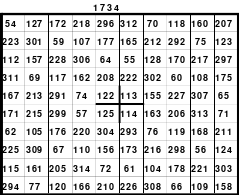
Auch hier sollte auf einen Hinweis, dass die 4 Quadrate der 5. Ordnung ebenfalls magisch sind, verzichtet werden.
(Die links abgebildete Matrix existiert nur in Ihrem Gedächtnis!)
Im Gegensatz zur Lösung bei der Vorgabe einer Zellenzahl, bestehen einige Probleme, die nachfolgend, sowie deren Behebung beschreiben werden.
Diese sind:
Da der Rest halbiert wird, muss dieser eine gerader Zahl sein und damit auch die Vorgabe. Bei einer ungeraden Zahl als Vorgabe sollte diese um eine Primzahl, wie bereits beim 6er Quadrat beschrieben, erhört werden. Das mag keine elegante Lösung sein, aber eine bessere hat Mag nicht gefunden.
Eine 4-stellige Zahl kleiner 2000 kann auch eine Zahl kleiner 1198 sein. Von dieser kann die magische Summe des Basisquadrates mit 1198 nicht abgezogen werden. Hier bieten sich, neben Anderen, 2 Lösungen an:
Mit den Worten “Nicht so zaghaft, etwas größer darf sie sein” (oder ähnlich) wird um eine größere Zahl gebeten, was allerdings unbeholfen wirkt. Hat aber Berechtigung, wenn es sich gleichzeitig um eine ungerade Vorgabe handelt, die zu einer geraden verändert werden muss.
Die bessere Lösung ist die Reduzierung der Flexzahlen auf | 0 | 30 | 60 | 90 | 120 |, was die Reserve noch zulässt. Die magische Summe des Basisquadrates wird dadurch um -200 auf 998 verkleinert. Diese Variante setzt allerdings voraus, dass es sich um eine gerade Vorgabe handelt.
Eine Nachbetrachtung
Haben Sie bei den Quadraten erkannt, dass diese 5 Zahlenreihen mit je 20 Zahlen enthalten, wobei die Zahlen bis auf wenige Fälle nur einen Abstand von 1 haben? Wenn nicht, werden es auch Ihre Gäste nicht erkennen. Sollte es ein Gast bemerken und äußern, was wahrscheinlich nie der Fall sein wird, so erklären Sie, dass dies mathematisch bedingt ist und weisen nochmals darauf hin, dass keine Zahl doppelt vorkommt und dass dies das Wichtigere ist.
Der Grund dieser Differenz von nur 1 erklärt sich aus den Abständen der Quadratzahlen.
Abhilfe könnte erreicht werden, durch eine Schlüsselzahl mit der alle Quadratzahlen multipliziert werden. Diese kann auch eine gerade Zahl sein, da die Folgezahlen in den Blöcken jeweils um 5 erhöht werden. Diesen zusätzlichen Aufwand an Berechnungen und Zeit sollte vermieden werden. Hinzu kommt, dass auch die magische Summe des Basisquadrates neu berechnet werden muss. Auch kann es zu doppelten Zahlen kommen.
Die Differenz zwischen den ersten Zahlen der Blöcke betragen natürlich auch meistens nur 1, was beim Eintragen der Zahlen sehr leicht erkannt wird. Deshalb sollte bei der Eintragung der Blockzahlen nicht sofort mit Sondersprung zum nächsten Quadrat gegangen werden, sondern 1 oder 2 Folgezellen mit Zahlen versehen werden. Diese sind im Rechtssprung zu erreichen und sind jeweils um 5 größer. Danach kann die Eintragung der 1. Zahlen der Blöcke fortgesetzt werden. Ein Vorteil dieses Verfahrens ist auch die Folge ungleicher Sprünge.
Diese Vorauseintragung stört die spätere Zahleneingabe in die restlichen Zellen der Blöcke nicht. Nach erfolgter Einsetzung aller 1. Zahlen der Blöcke erfolgt die Eingabe der Zahlen in die noch leeren Zellen. Dabei kann von jeder leeren Zelle ausgegangen werden. Man findet nach 2 bis höchstens 4 Rückwärtssprüngen eine Zelle mit Zahl. Von dieser aus können dann die weiteren Eintragungen fortgesetzt werden bis man auf eine Zelle mit Zahl gelangt, was die Fertigstellung dieses Blockes anzeigt.
Um größere Vorgaben zuzulassen sind 4 Wege möglich. So können 1. nur die Flexzahlen oder 2. alle Zahlen der Matrix mit einer Schlüsselzahl vergrößert werden. Eine solche Maßnahme sollte aber gut überlegt werden. Auch auf die 3. Möglichkeit sollte verzichtet werden. Bei dieser werden größere Vorgaben zugelassen ohne eine Veränderung der Matrix vorzunehmen. Die Folge sind unter Anderem bis zu 3-stellige Vorgabenteile und große Zahlenlücken zwischen den Blöcken. Als 4. können 3-stellige Vorgabenteile zugelassen werden, was ebenfalls keine gute Idee ist. Denn dann fehlen im Quadrat 1- und 2-stellige Zahlen und mit jedem Hunderter größer weitere 100. In fast allen Möglichkeiten kommt es zu einem schlechteren Zahlenbild und zu einer zusätzlichen Belastung durch das Merken weiterer Zahlen, was nicht notwendig ist.
Wer die Reduzierung der Flexzahlen bei Vorgaben der magischen Summe kleiner 1200 als zusätzliche Belastung ausschließe möchte, kann generell die Flexzahlen mit einer Differenz von 30 einsetzen. Allerdings können dann bei der Vorgabe einer Zellenzahl nur Vorgaben kleiner 200 abgefragt werden, wenn der Vorgabenteil 2-stellig bleiben soll.
Auf eine Wiederholung mit einer Vorgabezahl sollte verzichtet und dafür die Vorgabe einer magischen Summe angeboten werden. Der Grund ist, dass sich die gleiche magische Summe ergeben kann, was allerdings nur zu 2 % wahrscheinlich ist. Das trifft zu, wenn die Differenz zwischen 2 Vorgaben ganzzahlig durch 50 teilbar ist. Zum Beispiel bei Vorgaben 123 und 173. In beiden Fällen wird der Vorgabenteil 23 sein. Dem kann zwar abgeholfen werden, in dem z. B. beide Vorgaben den gleichen Blöcken zugeordnet werden. Dann werden die Vorgabenteile 23 und 73 groß und ergeben damit unterschiedliche magische Summen. Bei einer zweiten Vorgabe, die auch eine 2-stellige Zahl sein kann, bekommen Sie Probleme, wenn diese zufällig dem 2-stelligen Vorgabenteil einer vorherigen Vorgabe entspricht.
So können auch weitere zu vermeidenden Situationen entstehen. Das könnte z. B. eine größere magische Summe bei kleinerer Zahlenvorgabe sein. Bei der Vorgabe einer magischen Summe kann es zu einem völlig gleichen Quadrat kommen, obwohl die Vorgabe nicht der entstandenen magischen Summe einer vorangegangener Zahlenvorgabe entspricht.
Allgemein ist festzustellen, dass bei einem guten Verständnis des Systems zur Bildung eines 10er Quadrates im Hexen 1x1, auch andere Situationen erkannt und durch entsprechende Manipulationen ausgeschlossen werden können.
Trotzdem ist Mag der Meinung, dass keine Wiederholung und keine Veränderung des Basisquadrates die bessere Entscheidung sind!
Lediglich der Einsatz von Flexzahlen mit 30 als Differenz, ist bei der Vorgabe einer magischen Summe kleiner 1200 besser, als die fast peinliche Bitte um eine größere Zahl.
Bei der Vorgabe einer ungeraden Zahl als magische Summe wurde vorgeschlagen diese um eine Primzahl zu erhöhen. In diesem Fall sollte um eine 2-stellige Primzahl gebeten werden, weil eine 1-stellige auch die 2 sein kann und eine 3-stellige schwerer zu überprüfen ist. Ein Rechenkünstler muss wissen, ob die genannte Zahl auch eine Primzahl ist, sonst ist er unglaubwürdig. Die Prüfung ist ganz einfach.
Die Methode zur Ermittlung der Primzahlen wird als “Sieb des Eratosthenes” bezeichnet. Eratosthenes war ein alexandrinischer Gelehrte und lebte von 276 bis 194 v. Chr.. Die Methode besagt, dass eine Primzahl nicht durch eine Primzahl teilbar ist, die kleiner ist,
als die Wurzel aus der zu prüfenden Zahl.
Die Wurzel aus 100 ist 10. Die Primzahlen <10 sind 2, 3, 5 und 7.
Damit scheiden alle Zahlen als Primzahl aus,
die eine gerade Zahl sind,
deren Quersumme durch 3 teilbar ist und
die als letzte Ziffer eine 5 haben.
Bleibt nur die Prüfung auf eine Teilbarkeit durch 7 übrig, was bei 2-stelligen Zahlen nur das kleine 1x1 mit 7 erfordert.
Bei 3-stelliegen Vorgaben müsste die Prüfung um die Primzahlen <31,6, das sind 11, 13, 17, 19, 23, 29 und 31 erweitert werden, was nicht mehr so leicht in kurzer Zeit zu realisieren ist.
Zusammenfassung
Die gefundene Lösung kann durchaus als eine realisierbare eingestuft werden. Es werden keine hohen Anforderungen an die Rechenleistungen gestellt.
Auch das Merken der magischen Summe (1200-2), sowie der Aufbau der Matrix wird als realisierbar eingestuft. Dabei kann noch auf eine leichte Vereinfachung der Matrix hingewiesen werden. So können die Quadratzahlen für die Blöcke 2 und 3 als Blöcke 1 und 2 eingesetzt werden. Bei den folgenden Blöcken sind die Quadratzahlen 1 bis 5 abwechselnd ab - und aufsteigend eingeordnet.
Auch die Sprünge sind zu beherrschen, fanden diese doch insbesondere bei den vorangegangenen Experimenten mit den Springerquadraten Anwendung. Wie bereits erklärt, erfordern diese jedoch die volle Aufmerksamkeit, da die 5er Quadrate nicht verlassen werden dürfen.
Die Aussagen zur Matrix gelten für alle einfach gerade Quadrate, außer dem 6er. So auch für ein Quadrat der 14. Ordnung, dass aus 4 Korrekturquadraten der 7. Ordnung gebildet wird. Dabei können die Flexzahlen mit Abstand 50 beibehalten werden, weil 5*7=35 kleiner 50 ist! Allerdings müssen die magische Summe des 14er Basisquadrates und die Sondersprünge neu berechnet bzw. bestimmt werden. Nachfolgend der Kernteil der Matrix für 7er Korrekturquadrate.
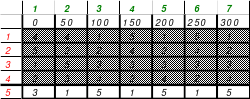
Das war nur eine theoretische Betrachtung, die zeigen soll, dass mit der erarbeiteten Lösung auch ein Quadrat der 14. Ordnung im Hexen 1x1 eine lösbare Aufgabe wäre. Allerdings sind hier die Multiplikation und Division mit 14 und nicht mit 10 erforderlich.
Es kann festgestellt werden, dass die Lösung für das 10er Quadrat ähnlich ist, wie die für das 6er Quadrat. Der wesentliche Unterschied besteht lediglich darin, dass die erlernte Zahleneinordnung im Lo-Shu-Quadrat beim 10er Quadrat durch erlernbare Sprünge und die Übergänge zwischen den Blöcken durch die Flexzahlen ersetzt werden. Des Weiteren wurde die Matrix für das 10er Quadrat etwas erweitert.
Mag schließt diesen Beitrag mit der Annahme ab, dass er nicht das Interesse aller Fans finden wird. Aber den Wenigen, die sich damit befassen werden, wünscht Mag viel Erfolg bei der Erweiterung Ihres Wissens über die magischen Quadrate.
6.9.2. Das Nullquadrat
Mag hat stets Quadrate mit den Zahlen von 1 bis n als Grundquadrate verwendet. Die 0 (Null) kam nicht vor. Das war der Tradition geschuldet. Die Null nicht in den magischen Quadraten einzusetzen, hat historische Gründe.
Das Lo-Shu-Quadrat ist das älteste bekannte Quadrat, denn es wurde bereits 1200 v. Chr. dokumentiert. Es kann angenommen werden, dass in diesem Zeitraum, oder danach, auch weitere Quadrate entstanden sind, zu einer Zeit, wo die Null nicht bekannt war. Erst um 700 n. Chr. wird in Indien das Zeichen der Null und damit das Positionsrechnen eingeführt. Im 9. Jahrhundert übernehmen die Araber die Null und das Positionsrechnen. Es dauert bis zum 12. Jahrhundert, bis das "Rechenbuch Muhammeds“ übersetzt und damit die Stellenschrift der Zahlen im Abendland eingeführt wird. Das ist der Grund, weshalb in allen aus früheren Zeiten übermittelten magischen Quadraten keine Null zu finden ist.
(Auch in den römischen Zahlen gibt es deshalb keine Null.)
Mag ist der Meinung, dass die Null auch in den magischen Quadraten Verwendung finden sollte, was in einigen Beispielen im Internet bereits zu erkennen ist. Negative Zahlen lehnt er dagegen strikt ab. Die Zuschauer können im Allgemeinen mit Null rechnen, das haben sie von Anfang an in der Schule gelernt. Rechnen mit negativen Zahlen fällt dagegen manchem schwer und kann das Interesse an der Vorführung mindern.
Die Null einzusetzen, bringt beim Top- und Pentaquadrat Vorteile.
Nachstehend die Nullquadrate des Top- und Pentaquadrat. Alle Zahlen in den Zellen wurden um 1 reduziert. Dadurch wird die Zelle 1 zur Zelle 0. Die magischen Summen verändern sich beim Topquadrat von 34 auf 30 und im Pentaquadrat von 65 auf 60.
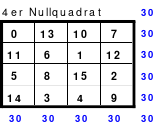
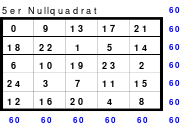
Mit diesen magischen Summen ist ein leichteres rechnen möglich, besonders bei Anwendung der Multimethode. Hier wird der Multiplikator durch Division der vorgegebenen magischen Summe durch die magische Summe des Grundquadrates errechnet. Eine Division durch 30 (3) bzw. 60 (6) ist leichter als die Division durch 34 bzw. 65.
Im Umkehrverfahren wird die magische Summe durch die Multiplikation des aus einer Zahlenvorgabe ermittelten Multiplikators mit der magischen Summe des Grundquadrates berechnet. Auch hier ist die Multiplikation mit 30 (3) bzw. 60 (6) leichter als mit 34 bzw. 65.
Auch bei der Anwendung der Duomethode können Vorteile genannt werden, die besonders beim 5er Nullquadrat hilfreich sind. Die ermittelte halbe Duosumme wird hier in die Zelle 12 (jetzt die mittlere) eingetragen. Der Rest kommt in die darunter befindliche Zelle 0. Ist kein Rest vorhanden, dann eben die Null. In die über der
mittleren Zelle 12 befindliche Zelle 24 (jetzt die größte) wird die volle Duosumme durch Multiplikation der Zahl in Zelle 12 mit 2 (*10/5) eingesetzt. Ein Abzug für die Zelle 1 entfällt.
Beim Topquadrat kann ebenfalls die volle Duosumme in die Zelle 15 (alt 16) eingesetzt werden und in die Zelle 0 gegebenenfalls die 0.
Im Einzelfall, wie bei der Routine “Start mit 2 Duos” im Abschnitt “Quadrate der 4. Ordnung” unter “Kleine Hexen 1x1”, kann der Vorteil jedoch nicht genutzt werden.
Auf weitere Details und Beispiele wird verzichtet. Sie können aus den bisher gemachten Ausführungen problemlos abgeleitet werden.
6.9.3. Rechnen mit Positionsblöcken
In den bisherigen Beschreibungen wurden mehrfach kleine Schlüsselzahlen wie 9, 7 oder gar 3 als weniger geeignet bezeichnet, da diese vom Zuschauer erkannt werden können. Der Einsatz größerer Schlüsselzahlen erfordern größere Vorgaben und damit eine erhöhte Rechenleistung, die wiederum eine längere Bearbeitungszeit erfordert. Auch wenn diese gering sein sollte, so ist zu bedenken, dass viele kleine Zeitverlängerungen am Ende eine spürbare werden kann.
Der Einsatz von “großen Schlüsselzahlen” können auch bei kleinen Vorgaben verwendet werden..
Die Beschreibungen werden am Beispiel des Pentaquadrat vorgenommen und können auf andere Primquadrate übernommen werden. Auch beim Topquadrat ist das möglich, wobei die Besonderheit des Topquadrates beachtet werden muss.
Die Lösung ist das Rechnen mit Positionsblöcken, kleinen und großen Schlüsselzahlen und einem verändertes Pentaquadrat.
Das muss im Einzelnen erläutert werden.
Das veränderte Pentaquadrat
Die Möglichkeit des Rechnens mit den Positionsblöcken hat Mag erkannt, als er das Pentaquadrat auswertete. Mag wird nicht auf Einzelheiten der Analyse eingehen, sondern nur auf die Ergebnisse, die das Rechnen mit Positionsblöcken (künftig P-Blöcke genannt) ermöglichen.
Aus den bisherigen Erläuterungen sind der Rösselsprung (Rechtssprung) und der Rückwärtssprung bei der Bildung und Berechnungen von Primquadraten bekannt. Zum besseren Verständnis der folgenden Erklärungen werden noch Linkssprung und Returnsprung genannt. Um was es sich dabei handelt ist in der Skizze zu erkennen.
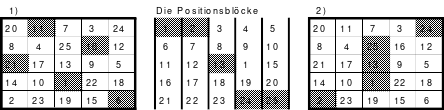
Das Quadrat 1 ist das um seine senkrechte Achse gedrehte Pentaquadrat.
Wird von Zelle 1 aus mit Rechtssprüngen zu den anderen Zellen gegangen, so kommt man durch die Drehung des Quadrates zu den Zellen 6, 11, 16 und 21 (grün Schattiert). Springt man weiter, kommt man zur Zelle 1, von der gestartet wurde.
Die Zellenzahl 1, 6, 11. 16 und 21 sind die ersten in den Blöcken 1 bis 5.
Genauso gelangt man zu den 2. Zahlen der Blöcke, wenn man von der Zelle 2 aus im Rechtssprung springt. Das trifft auch auf alle anderen zu und ist in der mittleren Tabelle dargestellt. Der 1. P-Block enthält alle ersten Zahlen der Blöcke 1 bis 5. der 2. P-Block alle zweiten, der dritte alle dritten usw. bis zum 5 P-Block mit den letzten Zahlen der 5 Blöcke.
Die Differenzen innerhalb der P-Blöcke sind einheitlich, die Ordnungszahl 5.
Diese Regeln ermöglichen es, mit diesen zu rechnen. Die oberen Zahlen 1 bis 5 sind die Startzahlen von denen aus den folgenden Zahlen aufsteigend berechnet werden. Von den unteren Zahlen 21 bis 25 werden die Zahlen der P-Blöcke absteigend berechnet.
Die Startzahlen werden ganz leicht gefunden. Da die Zelle 13 als mittlere u. a. bei der Berechnung der Größe aus der Summenvorgabe von Bedeutung ist, muss von dieser aus der mittlere P-Block berechnet werden. Unter der Zelle 13 ist die Zelle 1, die die Startzahl für die aufsteigenden Zahlen des 1. P-Blockes ist. Die Startzahl 2, die 1. Zahl im aufsteigend zu berechnenden 2. P-Block, findet man durch einen Linkssprung von der Zelle 1 aus. Um nach der Duomethode den Ausgleich zwischen den Zahlen zu erreichen, müssen die restlichen 2 P-Blöcke als absteigend zu berechnende gefunden werden. Die 25 ist eine solche und sie befindet sich über der Zelle 13. Zur Startzahl 24 gelangt man durch einen Returnsprung von der Zelle 25 aus. Damit sind für alle 5 P-Blöcke die Ausgangszahlen ermittelt und die Berechnung des Quadrates kann erfolgen. Siehe Quadrat 2.
Die zur Berechnung notwendige Schlüsselzahl wird wie bekannt berechnet, indem die Zahl in Zelle 13 durch 13 dividiert wird. Diese wird in dieser Routine als kleine Schlüsselzahl (kS) genannt. Da die Differenz zwischen den Zahlen der P-Blöcke der Ordnungszahl entspricht wird die kS mit der Ordnungszahl zur großen Schlüsselzahl (gS) multipliziert.
Doch nun zu einem praktischen Beispiel.
Mag lässt sich eine größere 2-stellige Zahl nennen. Es wird 53 genannt, die Mag in die von den Zuschauern bestimmte Zelle, die mittlere, einsetzt.
Die 53 multipliziert er mit 5 (bzw.10/2) und schreibt das Ergebnis 265 über das Quadrat.
Die Schlüsselzahl berechnet er mit 53/13 = 4 und wählt 3. Der Rest wird nicht weiter beachtet. Diese Schlüsselzahl ist die kleine. Die große Schlüsselzahl erhält Mag durch Multiplikation der kleinen mit der Ordnungszahl. Das ist 3*5 = 15.
Die weiteren Schritte der Berechnung sind:
Berechnung der Zahlen für den mittleren P-Block. Dazu wird 53+15=68 errechnet und nach einem Rechtssprung in die erreichte Zelle eingesetzt. Es folgt 68+15=83, die ebenfalls nach einem Rechtssprung eingetragen wird.
Die absteigenden 2 Zahlen werden mit 53-15=38 und 38-15=23 ermittelt und in Rückwärtssprüngen eingesetzt. (Siehe blaue Zahlen im Quadrat 3).
Die 53 wird durch Verdopplung (53*2=106) zur Duosumme berechnet. Von dieser hat Mag 17 für Zelle 1 (unter der 53), abgezogen und die verbliebenen 89 in die Zelle über der 53 geschrieben. Von dort ging es mit Rückwärtssprüngen zu den Zellen des 5. P-Blockes, in die die um jeweils 15 reduzierte Zahlen 74, 59, 44 und 29 eingesetzt wurden. Mit einem weiteren Rückwärtssprung gelangt man zurück zur Startzahl 89. Von dieser wird die kS = 3 abgezogen und nach einem Returnsprung in die erreichte Zelle als Startzahl für den P-Block 4 eingesetzt. Von dieser aus werden wieder in Rückwärtssprüngen die um jeweils 15 reduzierten Zahlen 71, 56, 41 und 26 eingetragen.
Die unter der 53 befindlichen 17 ist die Startzahl des 1. P-Blockes, dessen Zahlen um jeweils 15 zu erhöhen sind und nach Rechtssprüngen eingetragen werden. Gelangt man am Ende der Sprünge auf die mit 17 belegte Zelle, weiß man, dass der 1. P-Block fertig ist. Die 17 wird um die kS erhöht, das ist 17+3=20, die nach einem Linkssprung in die erreichte Zelle kommt. Es ist die Startzahl des 2. P-Blockes. Von dieser aus können in Rechtssprüngen die restlichen Zellen gefunden werden, in die ebenfalls die um jeweils 15 reduzierten Zahlen kommen.
Das Quadrat ist fertig. Es ist das Quadrat 4. Es ist magisch mit der magischen Summe von 265.
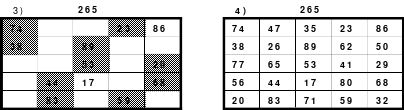
Wenn Sie alle Sprünge und Eintragungen entsprechend nachvollziehen, werden Sie erkennen, dass das System der Berechnung mit den Positionsblöcken eine leichte und übersichtliche Sache ist.
Durch die Bildung der großen Schlüsselzahl und deren Anwendung bei der Erhöhung und Reduzierung der Zahlen, wird es für den Zuschauer schwerer sein, diese Regel zu erkennen.
Eine Nachbetrachtung
Bei Vorgabe der magischen Summe wird die Zahl für Zelle 13, bzw. die mittlere Zelle, durch Division der Vorgabe durch die Ordnungszahl ermittelt. Alles Weitere läuft wie beschrieben ab. ein evtl. anfallender Rest wird in die Zelle 1 schrieben. Bei der Errechnung der Startzahl für den 2. P-Block muss der natürlich abgezogen werden.
Vorteilhaft ist, dass der Aufbau des Pentaquadrates nicht bekannt sein muss. Alle Schritte werden wie beschrieben durchgeführt. Das trifft auch auf größere Primquadrate zu.
Dieses System kann bei allen Primquadraten angewendet werden. Voraussetzung ist, dass diese nach der einfachen Springermethode gebildet wurden Danach müssen die laufenden Zahlen nach Rechtssprüngen, 2 nach rechts und 1 nach unten, eingesetzt werden. Die Übergänge von Bock zu Block sind 2 nach unten.
Diese Quadrate haben alle gemeinsam die Anordnung der Zelle 1 unter und die der letzten Zelle über der mittleren Zelle.
Die Startzahlen werden genauso gefunden, wie es im Pentaquadrat beschrieben ist. Von der vorangegangenen Startzahl, wird die kleine Schlüsselzahl abgezogen oder zugeschlagen und das Ergebnis nach einem Links- oder Returnsprung in die erreichte Zelle eingesetzt.
Die Primquadrate sind 100%ig homogen. Deshalb kann auch die Zelle, mit der begonnen werden soll vorgegeben werden.
Das Topquadrat ist kein Primquadrat. Deshalb muss dieses System angepasst werden. Die Kenntnis des Quadrataufbaus muss allerdings einwandfrei vorhanden sein, denn in diesem Fall sind die einzelnen Schritte zur Findung der richtigen Zelle nicht nach einem System möglich.
Die Zahlenvorgabe wird in die Zelle 16 eingetragen und in die Zelle 1 Null oder eine kleine Zahl. Die magische Summe ist das Doppelte der Summe aus beiden Zahlen.
Die kleine Schlüsselzahl (kS) wird wie üblich gebildet. Durch Multiplikation dieser mit 4 erhält man die große Schlüsselzahl (gS).
In die Zelle 2 wird die um die kleine kS erhöhte Zahl aus Zelle 1 eingesetzt und in die Zelle 15 eine um die kS verminderte Zahl aus Zelle 16. Von den Zellen 1 und 2 werden die restlichen 3 Zahlen als aufsteigende Zahlenreihe mit der Differenz der großen gS eingesetzt. Dabei ist die nächste Zelle die um 4 größere. Von Zelle 1 geht es zu den Zellen 5, 9 und 13. Diese sind die 1. in ihren Blöcken. Bei den Zellen 16 und 15 werden die Zahlen als absteigende Zahlenreihe ermittelt und in die jeweils um 4 kleinere Zellen eingetragen. Das wäre z. B. von Zell 15 aus, die Zellen 11, 7 und 3.
Ein Beispiel soll das Gesagte verdeutlichen, wobei die Reihenfolge zu Gunsten einer logischeren Vorführung leicht verändert wurde.
Als Zahl wurde 74 vorgegeben, die Mag in die Zelle 16 einsetzt.
Er addiert zu dieser 3 und multipliziert die Summe 77 mit 2 und schreibt das Ergebnis 154 über das Quadrat. (Siehe Startposition)
Er hat 3 für die Zelle 1 gewählt, weil diese im Gegensatz zur 74 eine ungerade Zahl ist, wodurch auch eine gerade Schlüsselzahl möglich ist.
Die kS errechnet er mit (74-3) /16 = 71/16 = 4,44 und wählt 4.
Die gS wird 4*4 = 16
Erst jetzt schreibt er in die Zelle 1 die 3 ein und berechnet die Zahlen des 1. P-Blockes durch Addition von 16 und setzt diese in die um 4 größeren Zellen ein. Das ist in Zelle 5 = 19, Zelle 9 = 35 und Zelle 13 = 51.
Anschließend werden die absteigenden Zahlen von der 74 in Zelle 16 aus bearbeitet. Das ist in Zelle 12 = 58; Zelle 8 = 42 und Zelle 4 = 26.
Nun wird die 3 in Zelle 1 um die kS auf 7 erhöht und in Zelle 2 eingesetzt, von wo die Berechnung des 2. P-Blockes erfolgt.
Zum Schluss wird 74-4=70 in die Zelle 15 geschrieben und der 3. P-Block analog erarbeitet.
Das Quadrat ist fertig und als das rechte abgebildet. Es ist magisch mit 154 als magische Summe.
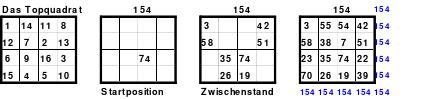
Bei einer Zahlenvorgabe entfällt ein Rest, weshalb in diesem Fall auch die Startzelle vorgegeben werden kann. Das ist bei einer Vorgabe der magischen Summe nur möglich, wenn die Vorgabe eine gerade Zahl ist.
Es ist möglich, dass Sie die Beschreibungen zu den Positionsblöcken verwirrend finden. Ist es aber nicht. Sie sollen aus den vielen Einzelberechnungen das System erkennen und erlernen. Dann wird auch diese Methode Ihr Gefallen finden.
6.9.4. Zum System “Einfach Clever”
Das System “Einfach Clever” hat Mag als Alternative zum 7er Königsquadrat erarbeitet. Später hat er es auf das Pentaquadrat übertragen und dort auch für die Routine “Vorgabe einer Primzahl” eingesetzt.
Das System baut auf das alternative Heptaquadrat auf. Das wurde durch Wenden des Haptaquadrates um die waagerechte Achse und anschließender Versetzung der untersten Zeile nach oben gebildet.
Das Ergebnis war eine aufsteigende Folge der Multizahlen und die Berechnung der Zahlen für die Zellen durch Abzug der Schlüsselzahl von der Zahl, die sich in der Zelle befindet, die 1 Zelle nach oben und 2 Zellen nach rechts zu finden ist.
Für das Pentaquadrat wurde als Ausgangsquadrat ebenfalls das um die waagerechte Achse gedrehte Pentaquadrat mit der Versetzung der unteren Zeile nach oben eingesetzt. Dadurch konnte ein gleiches Ergebnis erzielt werden, bis auf die Multizahlen, die jetzt absteigend angeordnet sind.
Eine aufsteigende Anordnung ist leicht erreichbar, indem das Pentaquadrat sowohl um die waagerechte, als auch um die senkrechte Achse gedreht wird und anschließend die unterste Zeile nach oben und die letzte Spalte nach vorn verschoben wird. Das so entstandene alternative Pentaquadrat ist das abgebildete.
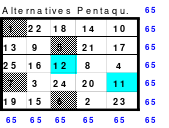
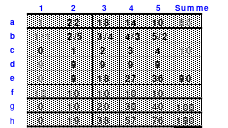
Die daneben abgebildete Tabelle zeigt die Veränderungen. Die Multizahlen sind von 0 bis 4 aufsteigend eingeordnet. Die Flexzahlen sind die gleichen, haben jedoch die Positionen getauscht. Auch die Primärzahl ist die gleiche.
Eine grundlegende Veränderung ist die Zuordnung der Zahlen im alternativen Quadrat. So ist die vorangegangene Zahl nicht mit 1 nach oben und 2 nach rechts zu finden, sondern 1 nach oben und 2 nach links. (Siehe farblich schattierte Zellen.)
Zweckmäßig ist, dass Sie sich für eine Option entscheiden. Wenn Sie vorwiegend mit dem Pentaquadrat arbeiten, ist die aufsteigende Variante vielleicht die bessere. Mag hat es in seinen Ausführungen bewusst bei der im Heptaquadrat angewendeten Version belassen, um so die Ausführungen zu vereinheitlichen.
6.9.5. Das Supereinfache (für Anfänger)
Die Berechnungen magischer Quadrate können einem Neuling anfangs evtl. wegen fehlender Übung schwerfallen. Das trifft bei Anwendung der Multi- und Duomethode sowie von “Einfach Clever” gleichermaßen zu.
Um Neulingen einen ersten Erfolg zu ermöglichen geht Mag einen Kompromiss ein und beschreibt zwei verhältnismäßig leichte Varianten zur Bildung eines Quadrates der 4. Ordnung bei Vorgabe einer 2- oder 3-stelligen Zahl.
Allerdings ist ein gefestigtes Wissen der Zahlenfolge im Topquadrat Voraussetzung!
Variante 1
Zur Vorführung
Vorgabe einer 2-stelligen Zahl
Mag bittet um eine 2-stellige Zahl aus dem oberen Bereich. Es wird 73 gewählt.
Mag schreibt die 73 in die Zelle 1. Über das Quadrat schreibt er 365 als die magische Summe. Anschließend füllt er zügig alle Zellen der Reihe nach mit Zahlen aus.
Das fertige Quadrat ist ein magisches.
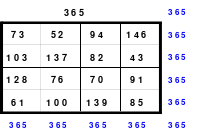
Die Lösung
Die Vorgabe 73 wird mit 5 multipliziert indem gedanklich eine Null angehängt und die 730 dann durch 2 geteilt wird. Das Ergebnis 365 ist die magische Summe.
Mag bildet einen Operator der etwa 1/3 von 73 ist. Er wählt 21,
(Der Operator darf nicht durch 9 teilbar sein, anderenfalls kann es bei einer Schlüsselzahl = 9 zu doppelten Zahlen kommen.)
Er setzt in die Zelle 14 die Zahl 73-21=52 und 73+21=94 in die Zelle 11 ein. In Zelle 8 setzt er die Zahl 73*2=146.
(Damit ist die Summe in der oberen Zeile 5*73!)
Die obere Zeile ist fertig und bietet die Grundlage für die Berechnung aller restlichen Zahlen. Als Schlüsselzahl wählte Mag die 9.
Das ist für Zeile 2: Zelle 12: gehört zum Block 3 wie die 11 und ist um 1 größer. Folglich ist die Zahl für Zelle 12 = 94+9=103.
Zelle 7: 1 kleiner als Zelle 8 = 146-9=137
Zelle 2: 1 größer Zelle 1 = 73+9=82
Zelle 13: 1 kleiner Zelle 14 = 52-9=43
In gleicher Weise werden die Zahlen für die Zeilen 3 und 4 berechnet.
Weitere Erklärungen sind nicht erforderlich, wenn die Ausführungen zur Bildung eines magischen Quadrates der 4. Ordnung und dessen Einsatz im Hexen 1x1 ausgewertet wurden. Das trifft auch auf die Berechnung des Quadrates bei Vorgabe einer 3-stelligen Zahl als magische Summe zu.
Vorgabe einer 3-stelligen Zahl
Es wird um Nennung einer größeren 3-stelligen Zahl gebeten. Es wird 783 genannt.
Mag bildet daraus das nachstehende magische Quadrat.
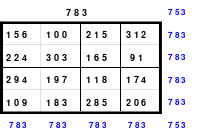
Lösung
Die Vorgabe wird durch 5 geteilt und ergibt 783/5=156 für Zelle 1 und einen Rest 3.
Als Operator wurde rd. 1/3 von 156 z. B. 59 (60-1) gewählt.
Der weitere Ablauf entspricht dem vorangegangenen mit der 2-stelligen Vorgabe, wobei lediglich der Rest 3 der Zelle 14 zugeschlagen wird.
Damit kommt in Zelle 14: 156-59+3= 100
Zelle 11: 156+59=215
und in Zelle 8: 156*2=312
Die Zahlen für die übrigen Zellen werden wie bereits beschrieben berechnet.
Variante 2
Vorgabe einer 2-stelligen Zahl
Einem Neuling kann es anfangs noch schwerfallen, die Zahlenfolge in den Zeilen einwandfrei zu beherrschen und damit auch die Quadratbildung entsprechend der „Hohen Schule“ wie bei Variante 1. Die Zahlen von 1 bis 16 in ihrer Reihenfolge (1, 2, 3, …. 16) einzusetzen wird bei dieser Variante vorausgesetzt.
Darbietung
Mag bittet um eine 2-stellige Zahl größer 30. Es wird 54 genannt, die in die Zelle 1 eingesetzt wird. Über das Quadrat schreibt Mag die Zahl 264. Anschließend füllt er alle weiteren Zellen mit Zahlen aus. Das so entstandene Quadrat ist magisch. Die magische Summe beträgt 264.
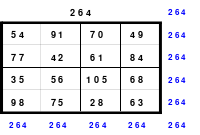
Lösung
Das Topquadrat wird als Nullquadrat eingesetzt. Alle Zellenzahlen werden um 1 kleiner. Aus Zelle 1 wird Zelle 0 und aus Zelle 5 die Zelle 4. Die magische Summe des Nullquadrates ist 30.
Die Quersumme der Vorgabe 54 ist 9 und folglich durch 9 teilbar. Zur Vermeidung von doppelten Zahlen scheidet deshalb 9 als Schlüsselzahl aus. Es wird 7 als Schlüsselzahl bestimmt.
Die magische Summe wird mit 30*7+54=264 berechnet und eingesetzt.
Nun folgen die übrigen Zellenzahlen. In Zelle 1/2 (neu/alt) wird die um 7 erhöhte Zahl 54, das ist 54+7=61 eingesetzt. In Zelle 2/3 kommt 61+7=68 und in Zelle 3/4 68+7=75.
Achtung: In Zelle 4/5 wird nicht eine weitere um 7 erhöhte Zahl eingesetzt, sondern 4*7=28. In den weiteren Zellen wird dann wieder eine um jeweils 7 erhöhte Zahl eingeschrieben. Das ist in Zelle 5/6 28+7=35. So wird weiter verfahren bis zur Zelle 15/16, für die 105 berechnet wurde. Zur Kontrolle: 15*7=105 - Richtig, keinen Fehler gemacht!
Vorgabe einer 3-stelligen Zahl
Die Vorgabe ist 738. Die Schlüsselzahl wird stark vereinfacht ermittelt. Dazu wird die letzte Ziffer weggelassen und die verbleibende Zahl 73 durch 3 (die 10er Ziffer der magischen Summe 30) geteilt und ergibt 73/3=24.
Es wird als Schlüsselzahl 19 gewählt.
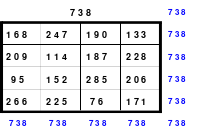
Die magische Summe für das Nullquadrat ist Schlüsselzahl*30, das ist 19*30, einfacher auch (20-1) *30=600-30=570. Diese wird von der Vorgabe abgezogen und man erhält 738-570= 738-600+30 =168 die in die Zelle 0/1 eingesetzt wird.
Alle weiteren Berechnungen erfolgen wie bei der Vorgabe einer Zahl für Zelle 0/1, jedoch mit der Schlüsselzahl 19.
6.10. Das Genie
6.10.1. Das Superhirn
Bei diesem Rechenexperiment wird kein magisches Quadrat gebildet. Es beruht aber auf der Grundlage eines teilmagischen Quadrates, weshalb sich Mag entschieden hat, es mit aufzunehmen.
Es ist schon Jahre her als Mag folgende Vorführung eines Rechengenies erleben durfte:
Der Rechenkünstler ließ bereits vor seinem Auftritt Karten im Publikum verteilen auf denen mehrstellige Zahlen (Multiplikand) vermerkt waren und die Bitte, diese mit einer vom Zuschauer frei gewählten mehrstelligen Zahl (Multiplikator) zu multiplizieren.
Dann kam sein Auftritt.
Mit der Frage, wer seiner Bitte nachgekommen sei, wandte er sich an einen sich meldenden Zuschauer und bat diesen, die von ihm vorgegebene Zahl und die vom Zuschauer gewählte Zahl zu nennen.
Nach kurzer Überlegung nannte er das Ergebnis (Produkt) dieser Rechnung. Er hatte also zwei mehrstellige Zahlen innerhalb von Sekunden im Kopf multipliziert.
Einem anderen Zuschauer nannte er das Ergebnis in Form der einzelnen Ziffern vorwärts und auch rückwärts gelesen.
Beim nächsten Zuschauer nannte er auch die Zwischenprodukte, die sich beim Multiplizieren der vorgegebenen Zahl mit den Einern, Zehnern usw. ergeben haben. Einmal nannte er die Zwischenergebnisse als komplette Zahlen, das andere Mal die Ziffern aus denen sich das Zwischenergebnis zusammensetzt in der Reihenfolge vorwärts und auch rückwärts.
Dann ließ er sich das Ergebnis (Produkt) nennen und seine Vorgabezahl. Sofort konnte er die vom Zuschauer gewählte Zahl (Multiplikator) nennen.
Er hatte das vielstellige Ergebnis durch die mehrstellige Vorgabezahl im Kopf in einer unfassbar kurzen Zeit dividiert.
Hatte ein Zuschauer einen Fehler in seinen Berechnungen, so fand der Meister diesen sofort heraus und nannte das richtige Ergebnis. Nach einer erneuten Berechnung durch den Zuschauer bestätigte dieser dann das richtige Ergebnis des Meisters.
So ging es ohne Langweile aufkommen zu lassen etwa 20 bis 30 Minuten. Er spielte mit den Zahlen wie ein Klaviervirtuose mit den Tasten seines Klaviers.
Selbst Mag, in Sachen Rechenkunst nicht unwissend, war von der Darbietung stark beeindruckt. Sie war genial und unerklärlich. Kein Wunder, wenn die Presse u. a. von einem Mann mit “Superhirn” sprach.
Mag war von der Darbietung so fasziniert, dass er vergaß Notizen zu machen. Heute weiß er, dass diese ihm nicht viel geholfen hätten. Oder können Sie aus den Zahlen (z. B.) 142857, 13571415, 857142, 2714283 und 9285705 eine Lösung ableiten? Es wird Ihnen wohl kaum gelingen.
Allerdings fragte sich Mag, warum der Rechenkünstler Zahlen vorgegeben hat und nicht auch diese vom Zuschauer hat frei wählen lassen? Auch erinnert er sich, dass der Rechenkünstler, nachdem ein Zuschauer die Zahlen genannt hatte, diesen einfach überging und sich dem nächsten Zuschauer zuwandte.
Das waren aber zu wenig Anhaltspunkte um eine brauchbare Lösung zu erarbeiten.
Bei den Recherchen zu den magischen Quadraten fand Mag im Nachschlagewerk “Schlag nach Natur”, Herausgeber VEB Bibliographisches Institut Leipzig, Ausgabe 1953 ein ganz besonderes teilmagisches Quadrat. Leider gab es keine Hinweise wann und von wem dieses gefunden, erdacht, bzw. errechnet wurde.
Nachstehend der Originaltext:
Wie ein Blitz aus heiterem Himmel kam Mag die Erkenntnis, dass er hier das Geheimnis des Rechenkünstlers mit dem Superhirn entdeckt hatte. Es ist nicht eindeutig die richtige Lösung, aber eine, mit der die gleichen Effekte erreicht werden.
Eine Analyse der Basiszahl
Die Ziffernfolge der Basiszahl 142857 ist stets die gleiche. Durch die Multiplikation der letzten Ziffer 7 erhält man die letzte und damit auch die erste Ziffer des Ergebnisses.
Beispiel: 142857 x 4 = 571428
Die erste Ziffer ist eine 5. In der Basiszahl steht links von der 5 die Ziffer 8. Also endet die Zahl mit einer 8. Die 8 am Ende bedeutet, dass die Basiszahl mit 4 multipliziert wurde, denn nur 7 x 4 ergibt eine Zahl mit der 8 als Einer.
Diese Aussage trifft auf alle Zahlen zu, die durch Multiplikation der Basiszahl mit den Zahlen von 1 bis 6 entstehen.
Auch bei der Multiplikation der Basiszahl mit Zahlen größer 6 gelten einfache Regeln. Auch dazu ein Beispiel:
142857 x 27 = 3.857.139
Da die Multiplikation der Basiszahl mit 7 = 999.999, oder auch (1.000.000 - 1) ist, wird der Multiplikand, auch Faktor genannt, durch 7 geteilt und man erhält so die Zahl für die Millionen. Im Beispiel 24 durch 7 = 3, Rest 6. Das Ergebnis beginnt folglich mit 3 Millionen.
Anschließend wird der Rest berechnet. Dazu wird die letzte Ziffer der Basiszahl (7) mit dem Rest = 6 multipliziert und man erhält als letzte Ziffer 2 (von 42). Rechts von der 2 steht in der Basiszahl die Ziffer 8. Folglich beginnen die Tausender mit 8. Und da sie die Basiszahl kennen ist der Rest des Ergebnisses 857.142.
Doch Halt! Die Basiszahl x 7 ist doch nicht 1 Million groß, sondern um 1 kleiner! Also muss vom Ergebnis noch 3-mal die 1 abgezogen werden. Die letzten 3 Ziffern werden dann 142 - 3 = 139 groß.
Das Ergebnis ist mit 3.857.139 gefunden!
Und damit auch das Geheimnis des Superhirns!
Nun zur praktischen Anwendung
Sicherlich wollen Sie kein Profi werden und sicherlich haben Sie nur selten die Möglichkeit sich als Rechenkünstler zu profilieren. Deshalb beschränken sich folgenden Erläuterungen nur auf die Anwendung von Vorgaben, die das 1- bis 6-fache der Basiszahl betragen. Die Vorgaben werden künftig (fälschlicherweise) auch als Zufallszahlen bezeichnet. Des Weiteren werden die vom Zuschauer frei gewählten Zahlen (Gastfaktor) auf zweistellige begrenzt.
Die erforderlichen Berechnungen, die Sie einwandfrei beherrschen müssen, sind dann:
Die Basiszahl muss vollkommen bekannt sein. So muss ohne nachzudenken das Wissen vorhanden sein, welche Ziffer vor oder hinter einer Ziffer der Basiszahl steht.
Das Einmaleins mit der 7 muss beherrscht werden. Nicht nur dass man das berechnen kann, sondern man z. B. wissen muss, dass die Zahl 56 das 8-fache von 7 ist, und die letzte Ziffer, im Beispiel 6 nur vorhanden sein kann, wenn eine Zahl mit Endziffer 7 mit 8 multipliziert wurde.
Die Division einer bis zu 3 Stellen großen Zahl durch die Zahlen 1 bis 7 muss zügig vorgenommen werden können.
Auch die Multiplikation einer 2-stelligen Zahl mit den Zahlen 1 bis 6 muss beherrscht werden
Das sind keine großen Rechenleistungen und können von einem “Rechenkünstler” ganz einfach erwartet werden.
Beispiel einer Darbietung
Nachdem der Rechenkünstler, nennen wir ihn Mag, Zettel und Bleistifte an Gäste, die sich für das Experiment bereit erklärt haben, verteilt hat, erläutert er was zu tun ist. Er bittet die Gäste, die auf dem Zettel notierte Zufallszahl mit einer frei gewählten 2-stelligen Zahl zu multiplizieren und das Ergebnis, sowie die 2-stellige Zahl auf den Zettel zu notieren. Nachdem eine kurze Pause zum Rechnen abgewartet wurde, kann die Vorführung beginnen.
Mag bittet einen der Gäste um Nennung der vorgegebenen Zufallszahl. Dieser nennt 571.428. Als nächstes bittet er ihn, die 2-stellige Zahl, mit der er die Zufallszahl multipliziert hat zu sagen. Er nennt die Zahl 59.
Nach einem nur wenige Sekunden dauernden Moment sagt Mag: “Das Ergebnis ist 33.714.252”, was der Zuschauer als richtig bestätigt.
Wie hat Mag das so schnell gelöst?
Ehe er das erklärt ein paar Begriffe, damit künftig Klarheit besteht, was gemeint ist:
Die Basiszahl 142857 ist ihnen bereits bekannt.
Der Faktor mit dem die Basiszahl multipliziert wird ist der Vorgabefaktor
Die Zahlen, die durch Multiplikation der Basiszahl mit dem Vorgabefaktor entstehen sind die Vorgaben, den Gästen gegenüber oft auch als Zufallszahl bezeichnet.
Die vom Gast gewählte 2-stellige Zahl ist der Gastfaktor
Die Multiplikation des Vorgabefaktors mit dem Gastfaktor ergibt den Gesamtfaktor.
Die Division des Gesamtfaktors durch 7 ergibt den Miofaktor und den Endrest.
Die Multiplikation des Endrestes mit der Basiszahl ist die Grundzahl. Die Grundzahl entsteht bei der Multiplikation des Gesamtfaktors mit der Basiszahl und entspricht der Multiplikation des Endrestes mit der Basiszahl, wobei die letzten Ziffern meist nicht der Ziffernfolge der Basiszahl entsprechen, weil von der Grundzahl der Miofaktor abgezogen werden muss.
Doch nun zur Berechnung
Während der Zuschauer die gesamte Zahl nennt, ermittelt Mag bereits den Vorgabefaktor mit dem die Basiszahl zur Vorgabe multipliziert wurde. Da die erste Ziffer der Zufallszahl die 5 ist, ist die letzte Ziffer die 8, und das heißt, die Basiszahl wurde mit 4 multipliziert. Den Vorgabefaktor 4 merkt sich Mag. Nennt nun der Zuschauer seine 2-stellige Zahl, den Gastfaktor, mit 59, multipliziert Mag diese mit seiner gemerkten 4 und erhält den Gesamtfaktor 236.
Diese 236 teilt er durch 7 und erhält: 236 / 7 = 33 als Miofaktor und den Endrest 5.
Sofort beginnt er auch schon zu sprechen:
“Das Ergebnis ist 33 Millionen“. Jetzt muss der Rest des Ergebnisses, die Grundzahl ermittelt werden. 5 x 7 (Endrest 5 x letzte Ziffer der Basiszahl 7) ist 35. Davon merkt er sich nur die letzte Ziffer, die 5. Wenn die letzte Ziffer der Vorgabe eine 5 ist, muss die 1. Ziffer eine 7 sein und die folgenden Ziffern 14, zusammen 714 und Mag spricht weiter: “714 Tausend”.
Der letzte Teil der Grundzahl müsste 285 sein. Von dieser Zahl muss jedoch noch der Miofaktor, die Millionenzahl, im Beispiel 33, abgezogen werden. Das ist 285 - 33 = 252 und Mag beendet seine Aussage mit: “und 252”
Auf den ersten Blick sieht das Ganze recht kompliziert aus, ist es aber nicht.
Wenn Sie sich richtig mit der Mathematik vertraut gemacht und die vorgeschriebenen Angaben gelernt haben, dann sehen Sie das Ganze als eine realisierbare Sache an.
Natürlich müssen Sie üben, üben und nochmals üben. Auch müssen Sie schon einige Voraussetzungen im Kopfrechnen mitbringen. Ohne dem geht garantiert nichts.
Nachdem Mag das Ergebnis eines weiteren Gastes erfolgreich berechnet hat, wendet er sich dem 3. Gast zu und lässt sich Vorgabezahl sowie Gastfaktor nennen.
Statt das Ergebnis zu berechnen, wendet er sich an den Gast mit den Worten:
“Das Ergebnis sieht nicht gerade attraktiv aus. Das können wir unseren
Gästen nicht zumuten“,
Dabei macht er eine wegwischende Handbewegung und wendet sich an den nächsten Gast.
Warum das? Was ist passiert?
Der Gast hat als Gastfaktor 42 genannt! 42 ist ganzzahlig durch 7 teilbar und das Ergebnis besteht dann fast nur aus der Ziffer 9.
Das Ergebnis wäre 142857 x 42 = 5.999.994 (42/7=6 ---> 6x (1.000.000-1) =6.000.000-6). An dieser Situation ändert sich nichts durch den Vorgabefaktor. Wäre dieser z. B. 3, so wäre dann das Ergebnis 17.999.982 (42x3=126 ---> 126/7=18, ---> 18 x (1.000.000 - 1) = 18.000.000 - 18 = 17.999.982).
Zurück zum 3. Gast. Vielleicht fällt Ihnen eine bessere Ausrede ein. Zum Beispiel mit den weiteren Worten: “Ziehen Sie doch bitte die Unglückszahl 13 von Ihrer 2-stellige Zahl ab und berechnen das Ergebnis neu. Ich werde später auf Sie zurückkommen”, was Sie auch machen sollten.
Weiter geht es mit dem 4. Gast.
Dieser nennt die Vorgabezahl 285.714, worauf sich Mag sofort an seine Gäste wendet und sagt:
“Bis jetzt habe ich große Zahlen multipliziert und das Ergebnis richtig berechnet. Nun werde ich die gewählte 2-stellige Zahl errechnen. Das ist ganz einfach. Man muss dazu nur das 1- oder gar 2-stellige Millionenergebnis durch die 6-stellige Zufallszahl dividieren.” (So ein Schwindler!)
Er bittet den 4. Gast um das Ergebnis seiner Berechnung. Dieser nennt als Ergebnis 9.714.276. Nach einem kurzen Moment nennt Mag die vom Gast gewählte 2-stellige Zahl mit 34.
Lösung:
Mag hat gewartet, bis ein Gast eine Vorgabezahl mit dem Vorgabefaktor 1 oder 2 nennt, denn dann ist die Berechnung leichter. Das war beim 4. Gast mit der Zufallszahl 285.714 der Fall.
Nennt der Gast die Vorgabezahl, weiß Mag auch schon den Vorgabefaktor.
Nennt der Gast das Ergebnis, errechnet er sofort den Gesamtfaktor. Diesen teilt er durch den Vorgabefaktor und hat damit den Gastfaktor, die 2-stellige Zahl des Gastes errechnet!
Im Beispiel: Vorgabezahl = 285.714 🡪 der Vorgabefaktor ist 2
Ergebnis = 9.714.276 🡪 1. Teil des Gesamtfaktors=9x7=63
Die 1. Ziffer der Grundzahl = 7..... 🡪 2. Teil des Gesamtfaktors = 5, denn wenn 1. Ziffer 7, dann letzte Ziffer 5 und die ergibt sich nur aus 5x7=35!
Der Gesamtfaktor (1. + 2. Teil) = 63 + 5 = 68
Dividiert durch Vorgabefaktor = 68 / 2 = 34 der Gastfaktor!
Auch hier hat Mag nur auf die Millionenzahl 9 und auf die erste Ziffer der Grundzahl, die 7, gehört, denn der Rest ergibt sich aus diesen Werten!
Zum Abschluss noch ein paar praktische Hinweise
Wahrscheinlich werden Sie nur wenige Möglichkeiten haben als Rechenkünstler zu agieren. Selbst Mag kann sich nur noch auf weniger als 10 Auftritte erinnern. Unbeschadet dessen, sollten Sie sich mit der Materie vertraut machen. Ergibt sich die Möglichkeit einer Darbietung, genügt es in der Regel ein paar Tage vorher mit täglich 10 bis 15 Minuten die Rechenregeln aufzufrischen.
Bereiten Sie Ihren Auftritt gut vor. Fragen Sie ihre Gäste, wer einen Taschenrechner oder ein Smartphon mit Rechner-App dabeihat. Informieren Sie, dass lediglich 2 Zahlen miteinander zu multiplizieren sind. Erst dann fragen Sie wer bereit ist, Ihnen bei der Vorbereitung des folgenden Experiments zu helfen. Denen, die bereit sind, übergeben Sie einen Briefumschlag (A6). Dieser enthält einen Zettel und einen kleinen Bleistift oder ein anderes Schreibutensil. Der Zettel enthält die Information an den Gast, was zu tun ist. Wie der aussehen könnte, ist nachstehend abgebildet.
Die Vorgabezahl sollte unbedingt per Hand eingeschrieben werden. So ist der kleine Schwindel mit der “Zufallszahl” etwas glaubwürdiger. Da oft eine geeignete Schreibunterlage fehlt, kleben Sie den Zettel (oben mit 3 Punkten) auf ein gleichgroßes Stück Pappe.
Überbrücken Sie die Zeit, die die mitwirkenden Gäste zum Rechnen benötigen mit einem anderen Rechenkunststück welches Sie kennen und können.
Von weiterer Bedeutung sind auftretende Fehler und der Umgang mit diesen. Dabei geht es nur um Fehler die der Zuschauer macht. Sie dürfen sich keine erlauben. Haben Sie einen Zuschauer gebeten wegen eines Fehlers das Ergebnis neu zu berechnen, so müssen Sie später zu diesem Zuschauer zurückkehren, um sich die Richtigkeit Ihrer Rechnung bestätigen zu lassen. Anderenfalls bleibt nämlich offen, ob nicht Sie den Fehler gemacht haben.
Eine zwar selten mögliche Situation ist das Auftreten gleicher Ergebnisse. Das ist der Fall, wenn das Produkt aus Vorgabefaktor und Gastfaktor nicht nur einmal auftreten.
So ergibt 571.428 (Vorgabefaktor 4) x 36 (Gastfaktor) = 20.571.408.
Das gleiche Ergebnis erhält man aus 857.142 (Vorgabefaktor 6) mal 24 (Gastfaktor).
In beiden Fällen ist der Gesamtfaktor 144 (4 x 36) bzw. (6 x 24) gleich.
Da ein solcher Zufall wahrscheinlich sehr selten eintritt, kann er vernachlässigt werden.
Als letztes möchte Mag den Rechenkünstler mit dem Superhirn bescheinigen, dass er trotz des vereinfachten Lösungsweges ein “Genie” war, denn er hat die Vorgaben auch in Millionenhöhe vorgegeben, das bedeutet 2-stellige Vorgabefaktoren und die Zuschauer durften 3-stellige Zahlen als Multiplikator wählen.
7. Helfer PC
7.1. Kontrollquadrat
7.1.1. Das Kontrollquadrat
Bevor Mag diese Excel-Anwendung “Kontrollquadrat” erarbeitet hatte, musste er zur Prüfung der Richtigkeit eines magischen Quadrates alle Zeilen, Spalten und Diagonalen mühsam mit dem Taschenrechner berechnen. Als er endlich, und das ziemlich spät, über einen Computer verfügte, konnte er die Quadrate in ein Arbeitsblatt einordnen und für die Zeilen und Spalten die “Auto-Summen” bilden. Trotzdem mussten die Diagonalen immer noch mit dem Taschenrechner berechnet werden, was sehr umfangreich werden konnte, wenn es um die Frage nach der Pandiagonalität ging. Mag erkannte, dass ein richtiges Programm zur Prüfung der erarbeiteten Quadrate hermusste. Mag hat deshalb die Excel-Anwendung “Kontrollquadrat” aufgebaut, was allerdings nicht einfach war, sondern teilweise sehr aufwändig und auch kompliziert, was jetzt nach der Fertigstellung nicht mehr so erkennbar ist. Jedenfalls hat Mag diese Datei mehrfach überarbeitet.
Doch nun zur Datei “Kontrollquadrat”.
Die Datei gliedert sich in 5 Bereiche:
Eingabe- und Ausgabebereich,
Kontrollbereich,
Bereich zur Bildung der fallenden Diagonalen
Bereich zur Bildung der steigenden Diagonalen
Bereich zur Bildung der Info-Sätze
In ein 20-mal 20 Zellen großes Quadrat (in der Abbildung nur 8 x 8) wird oben links das zu prüfende Quadrat, in der Regel mittels Kopierung, eingegeben. Im Beispiel ist es das Pentaquadrat. Sofort wird textlich mitgeteilt, ob ein Fehler vorliegt. Liegt kein Fehler vor, erfolgt die Aussage ob das Quadrat ein magisches ist. Wenn es magisch ist, erfolgt auch die Anzeige ob es pandiagonal und wie groß die Quadratsumme ist. Die Quadratsumme ist die Summe aller im Quadrat enthaltenen Zahlen. Sie ist unter anderem für die Bewertung von bestimmten Quadraten erforderlich.
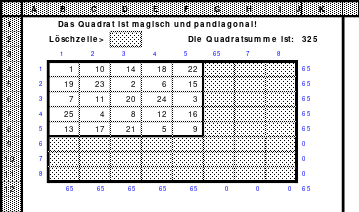
Zum Vergleich wird die normale Quadratsumme mit angegeben. Des Weiteren sind die Summen der Zeilen rechts neben dem Eingabefeld ausgewiesen und die Summen der Spalten sind unterhalb des Eingabefeldes zu sehen. Die Summe der fallenden Diagonale steht in der Zelle K12 und die der steigenden für ein Quadrat der 5. Ordnung in der Zelle G3. Sie sehen, das Quadrat wird ohne weitere Aktivitäten umfassend geprüft und das Ergebnis übersichtlich angezeigt.
Die eingegebenen Quadrate müssen nicht nur die Zahlen von 1 bis n enthalten. Es können auch Quadrate mit größeren Zahlen, wie sie u. a. bei den Multiquadraten oder Primzahlenquadraten entstehen, zur Prüfung eingegeben werden.
Für die Zellen des Eingabenbereiches hat Mag die Höhe 18 und die Breite 6 gewählt. Dieses Zellenformat ermöglicht die Darstellung des gesamten Kontrollquadrates auf einer Monitorseite. Die Breite lässt bei einem Schriftgrad von 10 bis zu 5-stelligen Zahlen zu. Die Zellen für die Zeilensummen, die fallende Diagonale und die Quadratsumme konnte eine Breite von 8 gewählt werden, was die Ausgabe von 8-stelligen Zahlen im Schriftgrad 8 ermöglicht. Derart große Zahlen werden bei Primzahlenquadraten oft anfallen. Werden in das Kontrollquadrat größere Zahlen als 5-stellig eingegeben, oder sind die Summenzahlen größer als 8-stellig, kommt es zur Ausgabe von Rautenzeichen (#####).
Mag empfiehlt in diesem Fall eine Änderung der Zellenbreite vorzunehmen. Dazu muss der Schreibschutz nicht aufgehoben werden.
Aus den Tabellen können auch weitere Informationen, u. a. über die Reihen, die nicht der einheitlichen Summe entsprechen, entnommen werden. Ob das Quadrat magisch ist oder nicht, wird im Kontrollbereich ermittelt und im Bereich “Bildung der Info-Sätze” als Infosatz formuliert. Gleiches erfolgt mit dem Kontrollergebnis zur Pandiagonalität, der Quadratsumme und Fehlerermittlungen. Einzelheiten sind im 5. Bereich zur Bildung der Info-Sätze enthalten. Die Ergebnisse aus diesem Bereich werden im Ein- und Ausgabebereich übernommen. Im Original sind das die Zellen B2 für die Fehleraussage, G2 für die Aussage ob magisch, H2 für die Aussage ob pandiagonal, Q1 und W1 für die Angabe der Quadratsumme und Q2 und W2 für die Ausgabe der normalen Quadratsumme. Dabei werden nicht alle Angaben zugleich ausgegeben. Liegt z. B. ein Fehler vor, so werden die anderen Angaben nicht angezeigt. Werden die genannten Zellen markiert, so kann die eingegebene Formel in der Bearbeitungszeile und die Formatierung der Zelle in der Symbolleiste eingesehen werden.
Über dem Kontrollquadrat sind die Spaltennummern angegeben. Wird ein Quadrat zur Kontrolle eingegeben, so erscheint in der Zelle rechts oberhalb des Quadrates die Summe der steigenden Diagonalen. Im Beispiel die Zahl 65 in der Zelle G3. Im Kontrollbereich wird die Ordnungszahl des zu prüfenden Quadrates ermittelt und in den Zellen N3 (für 3. Ordnung) bis N8 (für 8. Ordnung) durch 1 für Ja und 0 für Nein abgelegt. Unter Nutzung dieser Daten und der im Bereich 4 ermittelten und in Zelle AZ12 gespeicherten Summe der steigenden Diagonalen erfolgt die Eintragung derselben in die entsprechenden Zellen. Im Beispiel wurde in die Zelle G3 die Funktion =wenn (N3=1; AZ12;6) eingegeben mit dem Ergebnis, dass nur in der Zelle G3 die Summe der steigenden Diagonalen mit 65 ausgegeben wird. Wäre N3=0, so würde die 6 in dieser Zelle erscheinen.
Das Löschen der in den Eingabebereich eingegebenen Daten kann wegen der Sperrung nicht mit den Befehlen “löschen” oder “ausschneiden” erfolgen, sondern muss mithilfe der Löschzelle erfolgen. Dazu wird diese markiert und “kopieren” angeklickt. Danach wird der zu löschende Bereich markiert und mit dem Befehl “einfügen” wiederhergestellt.
Die Löschung wird in dieser Form nicht erforderlich, wenn nur 1 Quadrat geprüft werden soll. Dann kann beim Schließen der Datei die Frage “Änderung speichern?” mit “nein” beantwortet werden.
Sicherheit
Zur Gewährleistung der Sicherheit der Excel-Anwendung “Kontrollquadrat” ist die gesamte Datei schreibgeschützt, außer den Eingabebereich und der Löschzelle. Dieser Schreibschutz sollte nicht ohne zwingenden Grund aufgehoben werden, weil eine versehentliche Fehleingabe zu schweren Störungen des Programms führen können. Eine Fehlerbeseitigung ist dann äußert schwer zu realisieren.
Aus gleichem Grund sind die Spalten AC bis CZ, die die Berechnungen enthalten ausgeblendet.
Speziell für Fans - Der Lösungsweg
Aus technischen Gründen konnte dieser Bereich der Erläuterungen nicht hier übernommen werden. Er ist als gesonderte Datei “Erl. für Fans” vorhanden.
7.1.2. Speziell für Fans - der Lösungsweg (Für die Berechnungen im “Kontrollquadrat”)
1. Kontrollbereich
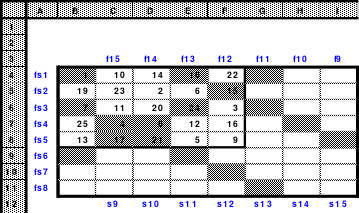
Nach erfolgter Analyse von Quadraten mit unterschiedlichen Ordnungszahlen erkannte Mag bestimmte Regelmäßigkeiten, die eine Bestimmung der zu einer geteilten Diagonale zugehörigen Teildiagonalen erleichtern. So sind in einem Quadrat einer bestimmten Ordnung die Differenzen zwischen 2 Teildiagonalen stets gleich. Diese Differenz kann als Konstante für fallende Teildiagonalen wie folgt ausgewiesen werden:
Kfn = Ok * 2 - 1 - Op. Dabei ist Kfn die Konstante für die fallenden Teildiagonalen eines Quadrates der n-ten Ordnung,
Ok die Ordnungszahl des Kontrollquadrates und
Op die Ordnungszahl des zu prüfenden Quadrates.
Dabei kann der Teil Ok * 2 - 1 als Konstante K für das Kontrollquadrat zusammengefasst werden.
Im Beispiel wird K = Ok * 2 - 1 = 8 x 2 - 1 = 15 und Kf5 = 15 - 5 = 10. Die fallende geteilte Diagonale F3 (gelb) setzt sich zusammen aus den fallenden Teildiagonalen f3 und f13 und 3 + 10 ist 13! Noch günstiger ist die Konstante bei den steigenden Teildiagonalen Ksn. Sie ist gleich der Ordnungszahl des zu prüfenden Quadrates. Im Beispiel also Ks5 = 5. Die steigende geteilte Diagonale F1 (blau) setzt sich zusammen aus der steigenden Teildiagonalen f1 und f6 und 1 + 5 ist 6!
Um zu prüfen ob das Quadrat ein magisches ist, muss nur festgestellt werden ob alle Zeilen, Spalten und Diagonalen eine einheitliche Summe haben. Ein Quadrat ist pandiagonal, wenn alle Diagonalen und geteilten Diagonalen ebenfalls die gleichen Summen ausweisen. Dazu müssen aber die Diagonalen und geteilten Diagonalen gebildet werden. Als erstes werden alle fallenden und steigenden Teildiagonalen durch Summierung der zugehörigen Zellen ermittelt. Die geteilten Diagonalen sind dann durch Addition der zugehörigen Teildiagonalen zu bilden. Dabei muss gesichert werden, dass nur die Diagonalen und geteilten Diagonalen des zu prüfenden Quadrates in den Kontrollbereich übernommen werden. Die richtige Auswahl erfolgt unter Nutzung der ermittelten Ordnungszahl.
Es ist nicht möglich und auch nicht erforderlich, alle in die Zellen eingegebenen Formeln aufzuführen. Mag beschränkt sich nur auf Beispiele, die durch Fettdruck im Text hervorgehoben sind. Damit Sie sich trotzdem über die Formeln informieren können, hat Mag in den folgenden Bereichen alle mit Formeln belegten Zellen hellblau schattiert. Sie brauchen nur eine solche Zelle zu markieren und können in der Bearbeitungsleiste die eingegebene Formel ablesen.
Den weiteren Lösungsweg können Sie den Erläuterungen zu den Bereichen 2 bis 5 entnehmen.
2. Kontrollbereich
Als erstes erfolgt hier die Ermittlung der Ordnungszahl für das zu prüfende Quadrat. Diese ist Ihnen sicherlich bekannt, aber aus ihr wird eine der wichtigsten Variablen gebildet, die für die weiteren Berechnungen notwendig ist. Die Ermittlung der Ordnungszahl macht die Eingabe derselben nicht erforderlich.
Die Tabelle dazu ist die linke. Die Ordnungszahlen wurden zweckmäßig so positioniert, dass die Ordnungszahl der Zahl des Datensatzes entspricht. Die zutreffende Ordnungszahl wird mit einer 1 gekennzeichnet, alle anderen mit 0. Dazu werden die Summen der Zeilen mit der jeweils nachfolgenden verglichen. Wenn die aktuelle Zeilensumme größer 0 ist und die folgende gleich 0, so ist die Ordnungszahl gefunden. Die Funktion dazu ist in unserem Beispiel für die Ordnungszahl 5 =wenn(und(K8>0; K9=0);1;0). Diese Formel wurde in die Zelle N5 eingegeben. Da K8=65 ist und K9=0, wird in der Zelle N5 die 1 ausgewiesen.
In der mittleren Tabelle erfolgt die Prüfung des Quadrates ob es ein magisches ist. Die Zeilensummen sind aus den Zellen K4 bis K11 in die Zellen Q4 bis Q11 zu übernehmen. Das erfolgt zum Beispiel mit der Summe der 3. Zeile mit der Formel =K6, die in die Zelle Q6 eingeschrieben wird. Analog werden die Summen der Spalten aus den Zellen B12 bis I12 in die Zellen T4 bis T11 übernommen.
Danach erfolgt der Vergleich mit der fallenden Diagonale des zu prüfenden Quadrates. Die fallende Diagonale wird im 3. Bereich gebildet und in der Zelle AN4 gespeichert. Von dort wird sie mit der Formel =AN4 in die Zelle X4 (blau umrandet) kopiert. Der Vergleich erfolgt z. B. mit der Zeilensumme in Q7 mit =WENN(UND(Q7>0; Q7<>X4);1;0), was in die Zelle R7 erscheint. Besteht Gleichheit, so wird in die jeweiligen Zellen R4 bis R11 eine 0 ausgewiesen, ansonsten eine 1. Gleiches geschieht mit den Summen der Spalten. Auch die steigende Diagonale muss verglichen werden. Die in den Zellen R4 bis R11 und U4 bis U11, sowie U13 enthaltenen Werte werden addiert und in der Zelle U14 ausgewiesen. Ist dieser Wert 0, so ist das Quadrat magisch.
Genau so wird mit den Diagonalen verfahren. Die fallenden Diagonalen werden im 3. Bereich berechnet und in den Zellen AN4 bis AN11 ausgewiesen. Die Berechnung der steigenden Diagonalen erfolgt im 4. Bereich und sind in den Zellen AZ4 bis AZ11 abgelegt. Die fallenden Diagonalen werden automatisch in die Zellen X4 bis X11 im Kontrollbereich übernommen und die steigenden in die Zellen AA4 bis AA11. Auch hier erfolgt der Vergleich mit der Summe der fallenden Diagonalen in Zelle X4. Das Ergebnis wird mit 0 für gleich und 1 für ungleich in die Zellen Y4 bis Y11 und AB4 bis AB11 eingesetzt. Ist das Ergebnis der anschließenden Addition 0, so ist das Quadrat auch pandiagonal.
3. Bereich zur Bildung der fallenden Diagonalen
Als erstes ist die Bildung der fallenden Teildiagonalen f1 bis f15 notwendig. Dabei werden alle Zellen der Teildiagonalen erfasst, ohne Beachtung der später zur Prüfung vorgesehenen Quadrate. Nicht vom zu prüfenden Quadrat mit Zahlen belegte Zellen enthalten den Wert 0 und beeinflussen die Summe der Teildiagonalen somit nicht.
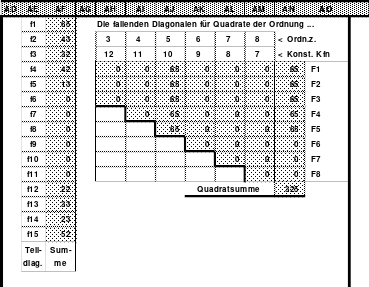
Die Summen der Teildiagonalen werden in den Zellen AF1 bis AF15 ausgewiesen. Die Einordnung der Reihe f1 bis f15 in die Datensätze 1 bis 15 erfolgte aus praktischen Gründen. Dadurch kann z. B. die Summe der fallenden Teildiagonalen f3 aus der Zelle AF3 und die von f13 aus der Zelle AF13 entnommen werden.
Die Summenbildung der fallenden Teildiagonale f3, als Beispiel, erfolge mit der in die Zelle AF3 eingegebenen Funktion =B6+C7+D8+E9+F10+G11 und die von f13 mit =E4+F5+G6+H7+I8 in Zelle Af13. Für das zu prüfende Quadrat der 5. Ordnung wird f3 =7+4+21+0+0+0=32 und f13 =18+15+0+0+0=33. Beide Teildiagonalen ergeben die fallende Diagonale F3 mit f3+f13=32+33=65 und das ist richtig.
Im rechten Bereich der Abbildung erfolgt das Zusammenfügen der Teildiagonalen zu den geteilten Diagonalen, wobei sich die fallende Diagonale F1 allein aus der Teildiagonalen f1 ergibt.
Es werden alle fallenden Diagonalen für alle Quadrate der 3. bis 8. Ordnung berechnet. Durch Multiplikation der Summen mit der zur Ordnungszahl gehörenden Variablen N3 bis N8 werden alle Summen der fallenden Diagonalen 0, wenn die Variable auch 0 ist. Ist sie 1, so werden die Summen angezeigt. Die Berechnungen erfolgten durch entsprechende Formeln in den blau schattierten Zellen. Mag zeigt die Formeln für das eingegeben Quadrat der 5. Ordnung, die sich in den Zellen AJ4 bis AJ8 befinden.
Durch Bildung der Auto-Summen in den Zellen AN4 bis AN11 werden die Summen aus den Zellen AJ4 bis AJ8 in diese übernommen. Des Weiteren wird die Auto-Summe von diesen Werten in der Zelle AN12 als Quadratsumme abgelegt.
4. Bereich zur Bildung der steigenden Diagonalen
Die Bildung der steigenden Diagonalen erfolgt wie die fallenden. Zuerst sind die Teildiagonalen zu bilden. So wird die Teildiagonale s1 in der Zelle AR1 mit der Formel =B4 gebildet und die Teildiagonale s5 mit der Formel =B8+C7+D6+E5+F4 in der Zelle AR5. Im Beispiel des 5er Quadrates ist das die steigende Diagonale F5 mit der Summe 13+4+20+6+22=65.
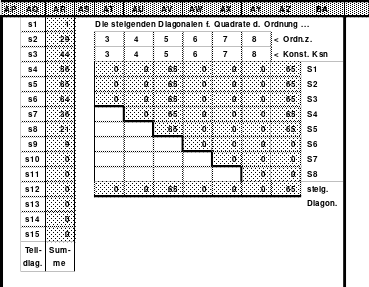
Die Berechnungen erfolgen durch entsprechende Formeln in den blau schattierten Zellen. Mag zeigt die Formeln für das eingegeben Quadrat der 5. Ordnung, die sich in den Zellen AV4 bis AV8 befinden.
Die Summe der ungeteilten steigenden Diagonale eines Quadrates befindet sich stets in der letzten Zelle der Summen für das jeweilige Quadrat. Für das 5er Quadrat in der Zelle AV8, für das 3er in der Zelle AT6, für das 7er in der Zelle AX10 usw., also in unterschiedlichen Zeilen. Eine Bildung der Summe mit der Funktion Auto-Summe ist deshalb nicht möglich. Mag übernimmt deshalb diese Summen in die Zellen AT12 bis AY12. Für das 5er Beispielquadrat wird in die Zelle AV12 die Formel =AV8 eingegeben. Für das 7er Quadrat ist die Formel =AX10 in die Zelle AX12 einzugeben. Die Summe der steigenden Hauptdiagonalen wird dann durch die Auto-Summe in Zelle AZ12 gebildet.
5. Bereich zur Bildung der Info-Sätze
Insgesamt werden folgende Info-Sätze gebildet, wobei sich der Satz über magisch und pandiagonal aus 2 Satzteilen zusammenfügt:
FEHLER! Quadrat < 3. Ordnung!
FEHLER! Kein Quadrat!
FEHLER! Falsche Eingabe!
Das Quadrat ist nicht magisch!
Das Quadrat ist magisch, aber nicht pandiagonal!
Das Quadrat ist magisch und pandiagonal! Die Quadratsumme beträgt: 9999
Im Beispiel ist die Aussage: Das Quadrat ist magisch und pandiagonal! Die Quadratsumme beträgt: 325
Die Satzbildung erfolgt von der weniger wichtigen zur höher wichtigen Aussage. Dabei wird, wenn zutreffend, der wichtigere anstelle des weniger wichtigen Satzes gebildet. Wenn nichtzutreffend, wird die weniger wichtige Aussage übernommen. Dieses k.o.-System wendet Mag an, weil die Funktionen in den Formeln nur 2 Aussagen zulassen. Richtig oder falsch.
Zum Fehlersatz
Um einen Fehler zu erkennen hat Mag eine Tabelle erstellt. In dieser werden alle mit Zahlen belegten Zeilen mit 1 angezeigt. Ansonsten mit 0. Gleiches geschieht mit den Spalten (Siehe nächste Seite). in den Zellen BD11 und Be11 werden diese Zahlen summiert.
Ist die Summe in BD11<3, so ist das Quadrat kleiner als das Miniquadrat der 3. Ordnung. Der Satz “FEHLER! Quadrat < 3. Ordnung!” wird gebildet.
Sind die Summen in BD11<>BE11, so wurde kein Quadrat eingegeben. Denn bei einem Quadrat ist die Anzahl der Zeilen gleich der Anzahl der Spalten. Der Satz lautet: “FEHLER! Kein Quadrat!”.
Wurde das Quadrat nicht wie vorgeschrieben in die Ecke oben links eingegeben, so ist die 1. Zeile oder die 1. Spalte gleich 0, bzw. beide zusammen kleiner 2. Hier wird der Satz: “FEHLER! Falsche Eingabe!”.
Diese Aussagen sind jedoch falsch, wenn im Kontrollquadrat überhaupt keine Zahl enthalten ist. Deshalb wird geprüft, ob die Summen in BD11 = 0 ist. Ist das der Fall, so wird kein Satz in der letzten Zelle zur Bildung des Fehlersatzes, in GB6, ausgewiesen.
Magisch oder nicht.
Im Kontrollbereich wurde geprüft, ob das Quadrat magisch ist. Es ist nicht magisch, wenn in der Zelle U14 eine Zahl größer 0 steht. Der Satz lautet dann: “Das Quadrat ist nicht magisch!”.
Steht aber in der Zelle eine 0, so ist das Quadrat magisch und der Satz ist dann: “Das Quadrat ist magisch”
Auch bei diesen Aussagen wird der Satz gelöscht, wenn eine Fehleranzeige erfolgt, oder keine Zahl im Kontrollquadrat eingegeben wurde.
Pandiagonal oder nicht
Des Weiteren wird im Kontrollbereich geprüft, ob das Quadrat pandiagonal ist. Es ist nicht pandiagonal, wenn in der Zelle AB13 eine Zahl > 0 steht. Es wird der Satz: “, aber nicht pandiagonal!” gebildet.
Ist die Zahl = 0, so heißt der Satz: “und pandiagonal!”.
Wurde ein Fehler festgestellt, oder ist das Quadrat nicht magisch, so entfällt dieser Satzteil. Ein Quadrat das nicht magisch ist, kann auch nicht pandiagonal sein.
Zur Quadratsumme
Liegt kein Fehler vor und wird eine Aussage zum Quadrat getroffen, so wird der Satz: “Die Quadratsumme beträgt:” gebildet.
Von dieser Aussage wird die Angabe der in Zelle AN12 enthaltenen Summe gemacht.
Die Formeln zur Bildung der Sätze können Sie der folgenden Übersicht entnehmen.
Die angegebenen Zellen beziehen sich dabei auf das Beispiel mit dem Kontrollquadrat der 8ten Größe. Im Original, dem 20er Kontrollquadrat, sind diese natürlich andere. Informationen dazu erhalten Sie durch Anklicken der blau eingefärbten Zellen. Die Ausgabe erfolgt dann in der Bearbeitungsleiste. Deshalb hat Mag auf die Beschreibung der Formeln und der betreffenden Zellen im Original verzichtet.
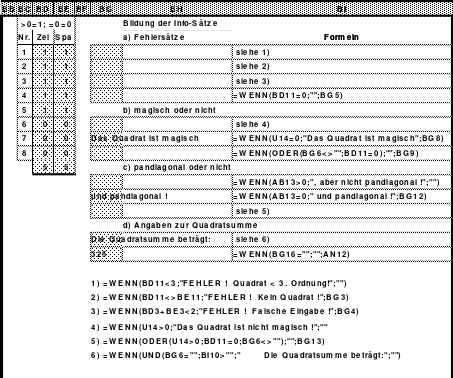
Natürlich hätte Mag auf die Bildung der Sätze in die Zellen BG6, BG10, BG14, BG16 und BG17 verzichten und die Formeln direkt in die Zellen B2, G2, H2, Q1 und W1 des Ausgabebereiches eingeben können. Mag hat wegen der besseren Übersicht aber darauf verzichtet.
Lediglich die später im Original zusätzlich aufgenommenen Aussagen über die normalen Quadratsummen hat Mag direkt in die Zellen U2 und W2 eingegeben. Diese sind im Original:
In Zelle U2: =WENN(BG16>””;”Quadratsumme normal:”;””) und
in Zelle W2:
=WENN(BG16>””;45*Z3+136*Z4+325*Z5+666*Z6+1225*Z7+65341*Z19+80200*Z20).
In Zelle W2 werden alle normalen Quadratsummen mit 1 oder 0 für die Ordnungszahlen multipliziert. Da nur die zutreffende Ordnungszahl mit 1 gekennzeichnet ist, wird die richtige normale Quadratsumme ausgewiesen. Die normale Quadratsumme ist die Summe aller Zahlen von 1 bis n eines Quadrates. Der Vergleich mit der tatsächlichen Quadratsumme ermöglicht Rückschlüsse auf eventuelle Fehler. Eine Differenz bedeutet aber nicht grundsätzlich, dass ein Fehler vorliegt. Differenzen treten u. a. bei der Prüfung von Nullquadraten, Multiquadraten, Primzahlenquadraten oder Teilquadraten aus einem Polyquadrat auf.
Auch wenn diese Excel-Anwendung mögliche Fehler ermittelt, so ist die Fehlersuche nicht 100-prozentig. Mag demonstriert das anhand des folgenden Quadrates der 5. Ordnung.
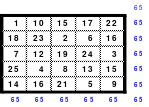
Das Quadrat ist magisch und pandiagonal. Auch die Quadratsumme ist mit 325 richtig. Die kleinste Zahl ist 1 und die größte 25.
Trotzdem weist dieses Quadrat einen Mangel aus. So sind die Zahlen 15 und 16 doppelt vorhanden und die Zahlen 11 und 20 fehlen. Dieser Mangel ist nicht durch Vergleiche von Summen wie bisher erkennbar, sondern erfordert den Vergleich jeder Zahl mit allen anderen. Das wären 79800 Vergleichsoperationen. Ein solcher Aufwand ist nicht zu vertreten. Mag empfehlen deshalb alle Spalten des zu prüfenden Quadrates untereinander in ein Arbeitsblatt einzugeben und absteigend zu sortieren. Durch Kontrolle können dann fehlende oder doppelte Zahlen erkannt werden.
Sicherheit
Zur Gewährleistung der Sicherheit der Excel-Anwendung “Kontrollquadrat” ist die gesamte Datei schreibgeschützt, außer den nicht schattierten Eingabebereich und der Löschzelle. Dieser Schreibschutz sollte nicht ohne zwingenden Grund aufgehoben werden, weil eine versehentliche Fehleingabe zu schweren Störungen des Programms führen können. Eine Fehlerbeseitigung ist dann äußert schwer zu realisieren.
7.1.3. Kontrollquadrat (Excel)
Die Datei
„Kontrollquadrat“
ist ein Excel-Programm, das nicht im Internet geöffnet werden kann. Um das Programm zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
7.2. Pendelquadrate
7.2.1. Berechnung von Pendelquadraten
Die Berechnung von Pendelquadraten zur Bildung von Kombiquadraten ist nach den bisherigen Erläuterungen sehr aufwändig und zum Teil auch kompliziert. Mag hat auch hier einen Weg gefunden, Pendelquadraten mittels der Software Excel zu bilden.
Dazu hat er die Datei “Pendelquadrate” erstellt, die hier verkleinert dargestellt wird. Im Original sind die einzelnen Bereiche 18 Spalten groß.
Die Datei gliedert sich in 3 Bereiche, den Eingabebereich, den Bereich der Berechnung und den Bereich der Ausgabe.
In den Eingabebereich werden das zu pendelnde Quadrat, die Anzahl der zu bildenden Quadrate und nacheinander des aktuell zu bildendem Quadrat eingegeben.
Im Beispiel sollen also 4 Pendelquadrate der 4. Ordnung erstellt werden, wovon gerade das 3. berechnet wurde.
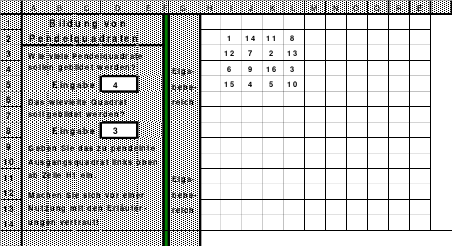
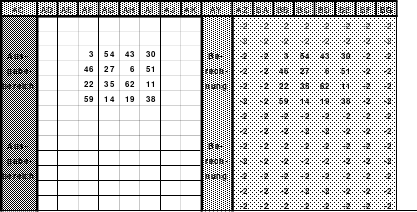
Nach erfolgter Eingabe wird das Pendelquadrat berechnet und angezeigt. Dabei werden formelbedingt auch die leeren Eingabezellen berechnet und angezeigt. Sie sind kleiner 1. Im Ausgabebereich werden diese dann gelöscht und nur noch das Pendelquadrat ist zu sehen. Dieses kann in ein gesondertes Arbeitsblatt kopiert werden, bevor die nächste Eingabe des aktuellen Quadrates erfolgt.
Zur besseren Übersicht wird empfohlen, durch Teilung den Ausgabebereich neben den grünen Teil des Eingabebereiches einzuordnen.
Die einzelnen Bereiche sind bis zur Zeile 300 programmiert und können eingesetzt werden,
Die Datei ist außer dem Eingabebereich schreibgeschützt. Dieser sollte nicht ohne zwingenden Grund aufgehoben werden.
Der Bereich der Berechnungen wurde aus Sicherheitsgründen ausgeblendet.
In gleicher Weise hat Mag ein Monsterquadrat der 3024. Ordnung gebildet. Ein Ausschnitt davon ist mit Erläuterung zum Aufbau dieses Quadrates im Anhang zu finden.
Hinweis: Das Pendeln von Nullquadraten ist nur bedingt möglich. Dazu muss ein Quadrat
mit den Zahlen von 1 bis n gependelt werden und anschließend sind alle Zahlen
der gependelten Quadrate um 1 zu reduzieren.
Ergänzende Erläuterungen für Fans
Im Abschnitt “Kombiquadrate” hatte Mag bereits die Pendelmethode beschrieben und auch Formeln für eine Berechnung vorgestellt.
Dies Formeln sind: Für die geraden Zahlen Zn=Za*Tg+1-Tn und für die ungeraden Zahlen Zn=(Za-1)*Tg+Tn
Es bedeuten: Zn = neue Zellenzahl
Za = Zellenzahl im Ausgangsquadrat
Tg = Gesamtanzahl der Teilquadrate
Tn = Das aktuell zu berechnende Teilquadrat
Za wird aus dem Eingabebereich entnommen, Tg wird in die Zelle D6 und Tn in die Zelle D9 eingegeben und können von dort abgerufen werden.
Die beiden Formeln hat Mag in einer Formel vereint und erweitert. Diese Formel wird in der Zelle AZ1 gebildet und bezieht sich auf die Zelle H1 im Eingabebereich.
Diese Formel lautet:
=WENN(H1/2=KÜRZEN(H1/2); H1*$D$9+1-$D$9;(H1-1) *$D$6+$D$9)
Die Formel unterteilt sich in 3 Teile;
=WENN(H1/2=KÜRZEN(H1/2); Prüfung ob die Zahl gerade oder ungerade ist
H1*$D$9+1-$D$9; Berechnung der geraden Zahl
(H1-1) *$D$6+$D$9) Berechnung der ungeraden Zahl
Diese Formel wird aus der Zelle AZ1 in alle Zellen der Berechnung kopiert, wobei sich die Bezugszelle automatisch anpasst.
Da der Computer die Ziffer 0 als gerade Zahl interpretiert, rechnet er im Beispiel folgerichtig nach der Formel =H1*$D$9+1-$D$9 =0*3+1-3=-2 für die Zelle AZ1 und alle anderen leeren Zellen. Bei Bildung des 1. Pendelquadrates werden alle leeren Zellen mit einer Null belegt, was sich ebenfalls aus der Formel ergibt.
In der Ausgabe werden zur besseren Übersicht alle Zahlen kleiner 1 gelöscht. Dazu wurde in die Zelle AD1 die Formel =WENN((H1>0); AZ1;””) eingegeben und von dort in alle Zellen des Ausgabebereiches kopiert.
Die Datei ist bis zur Zeile 300 programmiert und kann bei Bedarf erweitert werden
Um weitere Details der Berechnung einzusehen muss der ausgeblendete Bereich der Berechnung wieder eingeblendet werden.
7.2.2. Pendelquadrate (Excel)
Die Datei
„Pendelquadrate“
ist ein Excel-Programm, das nicht im Internet geöffnet werden kann. Um das Programm zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
7.3.Korrekturquadrate
7.3.1. Korrekturquadrate mit dem PC
Vorbemerkung
Der nachfolgende Text bezieht sich auf eine Works-Anwendung und wurde nicht wesentlich überarbeitet. Deshalb können Abweichungen in Dateinamen, Befehlen u. a. auftreten. Auch die Abbildungen können leichte Abweichungen gegenüber der überarbeiteten Excel-Anwendung enthalten. Die mathematische Lösung und die Übernahme dieser in eine computergestützte Lösung sind jedoch unverändert und verständlich.
Die Erläuterung
Nachdem Mag die PC-Lösungen “Pendelquadrate” erarbeitet hatte, stellte er sich die Aufgabe, auch eine Lösung für die Korrekturquadrate zu finden. Mag dürfte dies hervorragend gelungen sein. Im Teil “Bildung magischer Quadrate”, hat Mag im Abschnitt “Korrekturmethode” bereits die Lösung vorgestellt. Hier mussten die Wechselquadrate mit unterschiedlichen magischen Summen durch den Tausch von Blöcken so umgestaltet werden, dass im Ergebnis alle Quadrate gleiche magische Summen hatten.
Um einen Computer so zu programmieren, dass er die Korrekturquadrate errechnet und fertig ausgibt, erfordert eine mathematische Lösung mittels Formeln. Können diese nicht aus der Aufgabe herausgebildet werden, muss ein allgemeingültiger Algorithmus gefunden werden. Diese Aufgabe konnte Mag nach intensiver Suche lösen.
Nach erfolgreicher Bildung von Korrekturquadraten der 3. Ordnung (Die wegen der Unveränderlichkeit des Miniquadrates nur teilmagisch waren) erkannte er, dass für die Bildung der Korrekturquadrate nur 3 Blöcke notwendig ist. Das bedeutet allerdings auch, dass die übrigen Blöcke durch entsprechende Veränderungen gleich groß sein müssen.
Auf dieser Erkenntnis aufbauend suchte er nach entsprechenden Lösungen. Im Ergebnis fand er den Algorithmus, der die Bildung von Formeln ermöglicht. Das Ergebnis wird in den nachstehenden Tabellen vorgestellt.
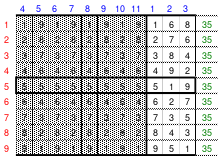
Links ist das Pentaquadrat, ein Quadrat der 5. Ordnung, dargestellt, wie eine Einordnung der Blöcke möglich ist, um alle gleichgroß zu gestalten. Es sollen insgesamt 9 Korrekturquadrate der 5. Ordnung entstehen. Die roten Zahlen sind die Nummern der 9 zu bildenden Korrekturquadrate. Die blauen stehen für die jeweils 5 Blöcke. Aus rechentechnischen Gründen sind die Blöcke 1 bis 3 rechts eingeordnet.
Alle schwarzen Zahlen besagen, aus welchem Wechselquadrat der entsprechende Block einzusetzen ist.
Zum Beispiel sind in das 3. Korrekturquadrat (rote 3) einzusetzen:
als 4. Block der 4. Block aus Wechselquadrat 3,
als 5. Block der 5. Block aus Wechselquadrat 7,
als 1. Block der 1. Block aus Wechselquadrat 3,
als 2. Block der 2, Block aus Wechselquadrat 8 und
als 3. Block der 3. Block aus Wechselquadrat 4.
Im grünen Bereich wird die gleich große Summe für die Blöcke 4 bis n durch eine gegenläufige Eintragung der Anzahl der zu bildender Quadrate erreicht. Die gegenläufige Eintragung erfolgt in die Blöcke mit ungerader Zahl, im Beispiel Block 5.
Bei den Blöcken 1 bis 3 konnte nicht so einfach verfahren werden. Die gefundene Lösung ist arithmetische Reihen, die im weißen Bereich die Ordnung unterbrechen. Diese Unterbrechungen lassen eine Regel erkennen, die auf alle Primquadrate zutrifft. Die Abbildung oben rechts ist das Quadrat der 11. Ordnung, für das ebenfalls 9 Korrekturquadrate erstellt werden sollen. Der weiße Bereich ist der gleiche. Das bedeutet, diese Ordnung trifft auf alle Primquadrate zu, für die 9 Korrekturquadrate gebildet werden sollen. Die weitere Analyse ergab, dass auch bei der Bildung einer anderen Anzahl von Korrekturquadraten diese Ordnung zutrifft, was am folgenden Beispiel gezeigt wird.
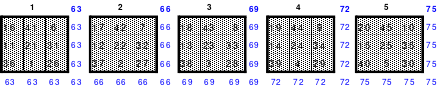
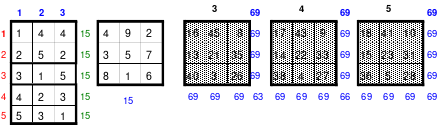
Es sollen 5 Korrekturquadrate der 3. Ordnung gebildet werden. In der oberen Reihe sind die 5 Wechselquadrate abgebildet und unten links die entsprechende Tabelle. Neben der Tabelle das Miniquadrat zur Orientierung und folgend die Korrekturquadrate 3 bis 5. Die Bildung der einzelnen Quadrate wird am Beispiel des 3. Korrekturquadrates erläutert.
In das 3. Quadrat (rote Zahl) wird als 1. Block (blaue Zahl) der 1.Block aus dem Wechselquadrat 3 eingesetzt (Magenta). Der 2. Block ist der 2. Block aus dem 1. Wechselquadrat (blau) und der 3. ist der 3. aus Wechselquadrat 5 (rot).
Alle 3 Korrekturquadrate haben die gleiche magische Summe 69. Da das Miniquadrat kein homogenes ist, sind die fallenden Diagonalen ungleich 69, außer im 5., dem letzten Korrekturquadrat, wo auch die fallende Diagonale 69 als Summe hat.
Mag hat diese Methode in mathematische Formeln gefasst. Auf der Grundlage dieser Formeln hat er eine Excel-Anwendung erarbeitet. Diese Datei mit den Namen ”Korrekturquadrate”. Sie unterteilt sich in einen Eingaben Bereich und einen Ausgabenbereich.
Im Eingaben Bereich werden lediglich die Ordnungszahl der Korrekturquadrate, die Gesamtzahl der zu bildenden Quadrate und das aktuell zu erstellendem Quadrat eingegeben. Diese Zellen sind zugleich die einzigen, die nicht gesperrt sind. Neben diesen Eingabefeldern befinden sich Kontrollfelder in denen “o.k.”, oder “Fehler” angezeigt werden. Dabei wird bei den Ordnungszahlen nur geprüft, ob es sich um eine ungerade Zahl handelt. Eine weitere Kontrolle erfolgt im Ausgabenbereich, die aber später beschrieben wird. Bei der Eingabe der Gesamtzahl wird kontrolliert ob es sich um eine ebenfalls ungerade Zahl handelt. Bei der Eingabe der Nr. des aktuellen Quadrates wird geprüft, ob die Nr. nicht größer als die Gesamtzahl ist.
Der Ausgabenbereich enthält Primquadrate der Größe 3 bis 19. Das sind Quadrate mit den Ordnungszahlen 3, 5, 7, 11, 13, 17 und 19. Durch “Teilen” der Datei kann das “richtige” Quadrat unmittelbar neben den Eingabebereich angeordnet werden. Das ist praktisch, denn sowohl Eingabe als auch Ausgabe können so auf den Monitor nebeneinander dargestellt werden. Nach den Eingaben der Ordnungszahl und der Gesamtzahl wird nacheinander die Nr. des aktuell zu erstellendem Quadrat eingegeben. Sofort nach dieser Eingabe wird das von Excel berechnete Quadrat mit Anzeige der Reihensummen ausgegeben. Nach Eingabe einer anderen Zahl für das aktuelle Quadrat wird auch dieses sofort berechnet und ausgegeben. Da es sich um Primquadrate handelt sind auch hier alle berechneten Quadrate pandiagonal. So können innerhalb von Minuten eine Vielzahl von Korrekturquadraten gebildet werden, die dann zu einem großen Quadrat zusammengestellt werden können.
Doch nun zu einem Beispiel.
Es sollen insgesamt 9 Teilquadrate der 5. Ordnung gebildet werden, um aus diesen ein magisches Quadrat der 15. Ordnung zu erstellen.
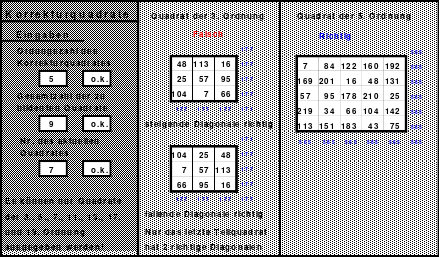
Nach Aufruf der Datei “Korrekturquadrate” werden die Ordnungszahl 5 und die Gesamtzahl 9 eingegeben. Im Ausgabebereich wird das Quadrat der 5. Ordnung als Richtig angezeigt. Daneben ist das Quadrat der 3. Ordnung als Falsch zu sehen. Diese zusätzliche Kontrolle soll die Arbeit erleichtern.
Es ist günstiger, dass Quadrat der 5. Ordnung durch Teilung unmittelbar neben der Eingabe einzuordnen, was besonders bei größeren Quadraten zwingend wird, weil diese sich sehr weit rechts befinden.
Nachdem als aktuell zu berechnendem Quadrat die 7 eingegeben wurde, wurde das 7. Teilquadrat mit der magischen Summe 565 angezeigt.
Sind alle 9 Teilquadrate ermittelt, können diese zum Quadrat der 15. Ordnung zusammengestellt werden. Da alle Teilquadrate gleich groß sind, ist eine bestimmte Einordnung nicht erforderlich.
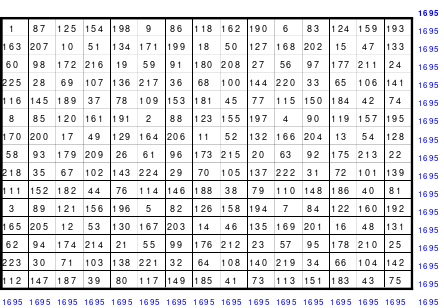
Das fertige Quadrat der 15. Ordnung, dass aus 9 Korrekturquadraten der 5. Ordnung gebildet wurde, ist oben dargestellt. Mag hat dabei bewusst auf eine Manipulierung des Quadrates durch chaotische Umgestaltung verzichtet.
In diesem Quadrat sind alle Zahlen von 1 bis 225 lückenlos enthalten. Es ist magisch aber nicht pandiagonal. Die magische Summe ist 1695.
Um z. B. ein Quadrat der 119. Ordnung zu erstellen, brauchten nur 7 x 7 = 49 Quadrate der 17. Ordnung in dieser Form gebildet und zusammengesetzt werden. In diesem Quadrat würden alle Zahlen von 1 bis 14161 lückenlos enthalten sein. Jedes der 49 Quadrate hätte die gleiche magische Summe von 120377 und das Gesamtquadrat der 119. Ordnung 842639 als magische Summe. Diese Aufgabe dürfte in weniger als 3 Stunden zu erledigen sein.
(Es darf aber gefragt werden “wozu das?”).
In der Datei “Erläuterg. f. Fans” werden die mathematischen Lösungen und die Programmgestaltung näher beschrieben.
7.3.2. Lösung - Erläuterung für Fans
Vorwort
Bevor Mag zur Erläuterung der Lösung kommt, sind einige Bemerkungen erforderlich. Jetzt, wo das Ergebnis vorliegt und dieses als leicht und logisch bewertet werden muss, war es jedoch nicht auf die Schnelle zu machen. Auch hier trifft zu:
“Es ist oft das Leichte, das schwer zu machen ist”
Der Lösung ging einige Versuche voraus, die aber nicht zu einem positiven Ende führten. Eine erste Lösung fand Mag vor rd. 20 Jahren, die auch den Einsatz des Computers analog der heutigen Fassung ermöglichte. Diese sollte Eingang in das “Hexen 1x1” finden. Als er begann die Lösung in Worte zu fassen, stellte er fest, dass er zwar den Aufbau der Formeln erkannte, aber nicht die Logik die zu den Formeln führte. Er musste folglich “das Fahrrad nochmals erfinden” und eine Lösung neu erarbeiten. Dem gefundenen Lösungsweg gingen auch diesmal mehrere Irrwege voraus. Auf der Grundlage der bisher erworbenen Kenntnisse zu den magischen Quadraten konnte eine Lösung gefunden werden, die nun erläutert wird.
Die Lösung
Der Grundgedanke einer möglichen Losung war der Tausch von Blöcken zwischen mehreren Quadraten. Das ist nur möglich, wenn einige Bedingungen erfüllt werden. Diese sind:
Alle im Tausch einbezogenen Quadrate müssen einen einheitlichen Aufbau haben. Diese Bedingung wird hauptsächlich durch Primquadrate erfüllt. Es kann angenommen werden, dass auch andere ungerade Quadrate eingesetzt werden können. Dazu wurden keine Überprüfungen vorgenommen. Andere ungerade Quadrate können meistens nach der Mosaikmethode aus korrigierten Primquadraten gebildet werden.
In der Gesamtheit der Quadrate müssen alle Zahlen von 1 bis n lückenlos und nur einmal enthalten sein.
Die Differenzen der magischen Summen zwischen den Quadraten müssen so klein wie möglich sein. Die 2 weiteren Bedingungen werden von Wechselquadraten erfüllt. Die Wechselmethode wurde bereits erklärt, trotzdem eine kleine Wiederholung.
Die Wechselmethode
Bei der Wechselmethode werden die Zahlen in fortlaufender Reihenfolge wechselweise in die Quadrate eingetragen und zwar stets von links nach rechts. Das ist in den folgenden 5 Quadraten der 3. Ordnung zu erkennen. Der 1. Block (blau) mit den Zahlen 1 bis 5 und der 2. Block (grün) mit den nächsten Zahlen 6 bis 10.
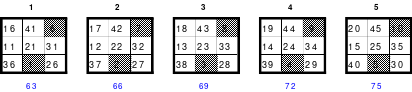
Alle Quadrate sind magisch jedoch mit unterschiedlichen magischen Summen. Die blaue Zahl unter den Wechselquadraten ist die jeweilige magische Summe.
Rechts ist das Basisquadrat abgebildet.
Da die Zahlen nach einer festen Regel eingetragen werden, ist auch eine mathematische Formulierung gegeben. Die Formel lautet:
Zn = Za * WQg - WQg + WQx Darin bedeuten:
oder auch Zn = Die neue Zellenzahl im Quadrat WQx
Zn = (Za - 1) * WQg + WQx Za = Die Zellenzahl im Ausgangsquadrat (Basisqu.)
WQg = Anzahl der zu bildenden Wechselquadrate
WQx = Das aktuell zu berechnende Wechselquadrat
Zum Beispiel die Berechnung der neuen Zellenzahl im Wechselquadrat 3 für die Zellenzahl 2 im Basisquadrat:
2 * 5 - 5 + 3 = 8 oder auch (2 - 1) * 5 + 3 = 8
Dieser Formel kommt eine entscheidende Rolle bei der Bildung korrigierter Quadrate zu, was Mag in der Vergangenheit nicht beachtet hat. Um das zu erkennen sind weitere grundsätzliche Gedanken für den Lösungsweg erforderlich.
Die gesuchten korrigierten Quadrate sollen gleichgroße magische Summen haben, was durch Tausch der Blöcke erreicht werden soll.
Da die weiteren Zahlen im Block nach gleicher Ordnung gebildet werden, genügt es, nur die ersten Zahlen des Blockes in die Betrachtung einzubeziehen.
Wenn die magischen Summen aller korrigierten Quadrate gleichgroß sein sollen, so müssen die Summen der 1. Zahlen der Blöcke im korrigierten Quadrat ebenfalls in jedem Quadrat gleichgroß sein.
Da jeder Block eines Wechselquadrates nur einmal eingesetzt werden kann muss die Anzahl der Wechselquadrate gleich der zu bildenden Quadrate sein. Das die Ordnungszahl ebenfalls die gleiche Größe haben muss ist selbstverständlich.
WQg, die Anzahl der Wechselquadrate ist gleich der Anzahl der zu korrigierenden Quadrate. Dieser Wert ist durch die Eingabe bekannt.
Za, die Zellenzahl im Basisquadrat ist bekannt, bzw. kann leicht aus der Eingabe der Ordnungszahl berechnet werden. Die Ordnungszahl wird ebenfalls eingegeben.
WQx, das Wechselquadrat, aus dem der Block entnommen werden soll ist damit die einzigste unbekannte Größe, die ermittelt werden muss.
Der Weg zum WQx
Um die Beschreibungen zu verkürzen, werden die noch nicht bekannten Glieder in den Formeln benannt:
KQ = Korrekturquadrat
KQg = Gesamtzahl der zu bildenden Korrekturquadrate
KQm = Das mittlere der “ “ “
KQa = Das aktuell zu erarbeitende KQ
BQ = Das Basisquadrat
O = Ordnungszahl der Quadrate (gleich für KQ, WQ und BQ)
B = Block-Nr. des BQ
Zb = 1, Zahl im Block des BQ
S = Schlüsselzahl, entspricht KQm
MS = Die magische Summe
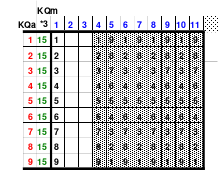
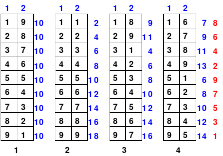
Zur Erleichterung der Lösungsfindung erstellte Mag als erstes eine Matrix für ein Quadrat der 11. Ordnung (O), für das 9 Korrekturquadrate (KQg) gefunden werden sollen. Die roten Zahlen stehen für die 9 Korrekturquadrate (KQa = KQ1 bis KQ9). Die blauen Zahlen sind die Blöcke für die Korrekturquadrate (KQ) und die Wechselquadrate (WQ) und die schwarzen Zahlen sind die WQ aus denen die Blöcke für die KQ entnommen werden.
Der grüne Bereich war schnell erledigt, indem einmal die Zahlen für die WQ von oben nach unten und einmal von unten nach oben eingeordnet wurden. So wird gesichert, dass gleiche Summen in die 9 KQ übertragen werden. Natürlich sind die Duosummen für die Blöcke (B) 4 und 5 nicht gleich der Duosumme der B 6 und 7. Denn das würde bezogen auf das KQ1 bedeuten, dass der B4 im WQ1 dem B6 gleicht, was nicht sein kann. Dieses Verfahren entspricht praktisch der Pendelmethode und kann nicht bei den restlichen Blöcken 1 bis 3 angewendet werden. Hier musste eine andere Lösung gefunden werden.
Da die Zahlen im grünen Zeilen die einheitliche Summe von 40 ergeben, müssen die restlichen drei im weißen Bereich ebenfalls gleiche Summen erbringen, anderenfalls würden die magischen Summen der KQ nicht gleich sein. Diese Summen sind jeweils das 3-fache der mittleren Anzahl von KQg, das ist KQm = 3 * 5 = 15. Dieser Wert ist in der Matrix mit grünen Zahlen eingesetzt.
Als erste setzte Mag für den B1 die Zahlen 1 bis 9 absteigend für die WQ ein, aus denen die ersten Blöcke für die KQ zu entnehmen sind. Es ist egal wo welche Zahl steht, es muss immer die Ergänzung zur Summe 15 gefunden werden.
Es musste nur das WQ ermittelt werden, aus dem der Block für das Korrekturquadrat zu entnehmen ist, denn das 3. WQ (WQ3) ergibt sich aus dem Wert 15 abzüglich der beiden Werte für B1 und 2.
Es bedurfte keiner großen Überlegungen welche WQ für die Entnahme der zweiten Blöcke einzusetzen waren. Die Kombinationen entsprechen der Abb. 1 bis 3 scheiden aus. Eine gegenläufige Eintragung (1) bringt nur gleiche Summen zustande. Gleiche Zahlen ergeben nur gerade Summen (2) und erfordern zum Teil Ergänzungszahlen kleiner 0 und größer 15. Gleiche Probleme treten auch in der Kombination 3 auf.
Mag stellte ganz einfach die Frage, welche Zahl muss für den 2. Block stehen, wenn der Wert für den Block 1 gleich 9 ist und für den 3. Block der Wert 1 angenommen wird. Das ist 5, die Mag zur Grundlage der Eintragung der weiteren Zahlen entsprechend der Regel von oben nach unten machte
Das Ergebnis ist die Zahlensäule 4. Die Summen sind die blauen Zahlen und die Differenz zur 15 sind die roten Zahlen, die von 1 bis 9 nur einmal vorkommen. Damit
war die gestellte Aufgabe erfüllt und die Zahlen für die Blöcke 1 bis 3 konnten in die Matrix eingesetzt werden.
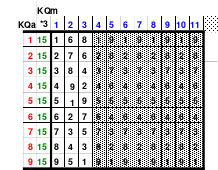
Ehe der gewählte Lösungsweg weiterverfolgt wird, ist eine Kontrolle des bisherigen Ergebnisses sinnvoll.
1. Test
Für einen Test sollen die weiter vorn bereits gebildeten 5 WQ zum Einsatz kommen.
Zuerst jedoch noch ein paar Regeln zu den WQ. Alle WQ sind magisch, haben jedoch unterschiedliche magische Summen (MS). Die Differenzen betragen das n-fache von +/-3, was der Ordnungszahl (O) entspricht.
Die Differenzen zwischen den Blöcken innerhalb jedes WQ entsprechen mit 15 dem Produkt aus Ordnungszahl (3) und der Anzahl der gebildeten Wechselquadrate (5). Das ist in diesem Fall 3*5=15.
Die Differenzen zwischen den Zahlen eines Blockes betragen einheitlich 5, das ist die Anzahl der WQ. Dieser Regel kommt eine besondere Bedeutung zu, denn nach dieser werden, ausgehend von der 1. Zahl im Block, alle weiteren Zahlen des Blockes berechnet.
Die aufgezeigten Regeln gelten generell.
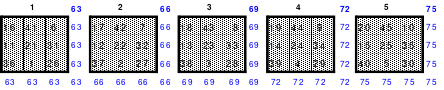
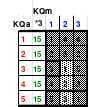
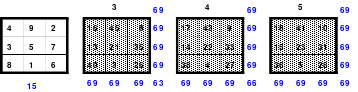
Zur Durchführung des Tests wurde eine Matrix für 5 Quadrate (rote Zahlen) und die Blöcke 1 bis 3 (blaue Zahlen) gebildet. Die Anzahl der Blöcke entspricht der Ordnungszahl des eingesetzten Miniquadrates.
Daneben ist zur Orientierung das Miniquadrat als Basisquadrat abgebildet.
Es sollen die korrigierten Quadrate 3, 4 und 5 erstellt werden.
Quadrat 3 (KQ3)
Für den B1 im KQ3 wird der B1 aus WQ3 mit den Zahlen 3, 8 und 13,
für den B2 der B2 aus WQ1 (16, 21 und 26) und
für den B3 der B3 aus WQ5 (35, 40 und 45) eingesetzt.
Das so entstandene KQ3 (untere Reihe) ist ein teilmagisches Quadrat mit der MS von 69, die dem Mittelwert der 5 magischen Summen der 5 Wechselquadrate und damit dem WQ3, dem mittleren, entspricht.
Das KQ3 ist nur teilmagisch, da die fallende Diagonale mit 63 nicht gleich der MS 69 ist. Das ist logisch, denn der 2, Block, der die fallende Diagonale bildet, stammt nicht aus dem 3. WQ.
KQ4
wird wie KQ3. gebildet. Für die Blöcke 1, 2 und 3 werden die Blöcke 1, 2 und 3 aus den WQ 4, 2 und 3 übertragen.
Auch dieses Quadrat ist nur teilmagisch, hat jedoch die gleiche magische Summe von 69.
KQ5
wird ebenso erstellt. Für die Blöcke 1, 2 und 3 werden die Blöcke 1, 2 und 3 aus den WQ 5, 3 und 1 übernommen.
Dieses Quadrat ist 100-prozentig magisch mit der MS von 69 in allen Reihen, auch in der fallenden Diagonale. Der Grund dafür ist, dass in das letzte KQ (KQg) als B2 die fallende Diagonale des mittleren Quadrates (WQm hier WQ3) eingesetzt wird. Es ist die einzigste fallende Diagonale in allen WQ mit der MS 69. Diese Diagonale existiert nur einmal und kann folglich nur einmal vergeben werden. Sie wird stets im letzten zu korrigierendem Quadrat (KQg) die fallende Diagonale bilden, was aus der Matrix zu erkennen ist.
Damit ist die Richtigkeit des eingeschlagenen Lösungsweges bestätigt.
Das trifft auch, zwar bedingt, auf das Miniquadrat zu, weshalb es in das Programm aufgenommen wurde.
Die Algorithmen
für WQx
Die Algorithmen für WQx sind schnell zu finden. Dazu wurden die Matrizen für ein Quadrat der 5. Ordnung erstellt, für das 9 korrigierte Quadrate gefunden werden sollen und für ein Quadrat der 11. Ordnung für das 13 Quadrate mit gleichen magischen Summen zu bilden sind. Die aus einer Matrix abgeleiteten Algorithmen sind nur gültig, wenn sie auf beide Matrizen zutreffen.
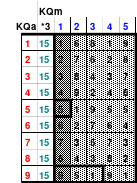
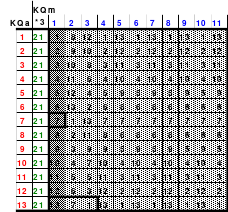
Es können 5 Bereiche (grün, blau, gelb, rot und grau) ausgemacht werden, deren Strukturen sich unterscheiden.
WQx im grünen Bereich (Blöcke >3) - In den geraden Blöcken sind die Zahlen 1 bis 9 für die WQ1 bis WQ9 aufsteigend eingeordnet. Das ist gleich der Einordnung von KQa. In den ungeraden sind sie absteigend eingeordnet.
WQx im blauen Bereich (Block 1) - Hier ist WQx gleich dem KQa
WQx im gelben Bereich (oberer Teil Block 2) - WQx ist um 1 größer als das mittlere KQm. KQm ist die Hälfte von MQ1 + MQg und ist auch die Größe der Schlüsselzahl S. Die folgenden Zahlen werden absteigend eingesetzt.
WQx im roten Bereich (unterer Teil Block 2) - WQx ist um 1 größer als KQa - KQm (KQm ist auch die Schlüsselzahl).
Die 1 wird in der Mitte eingeordnet. Anschließend werden die folgenden Zahlen absteigend eingetragen.
Damit kann festgestellt werden, dass alle Zahlen aus der Anzahl der zu bildenden Quadrate und deren Ordnungszahl abgeleitet werden können. Diese Werte werden im Eingabebereich eingegeben und stehen damit zur Berechnung zur Verfügung.
Diese sind: Zelle B7 = Ordnungszahl, Zelle B10 = Anzahl der zu bildenden Quadrate Zelle B13 = Das aktuell zu erstellende Quadrat
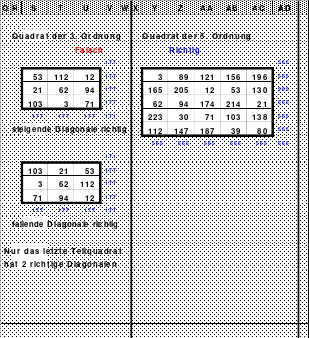
Die Berechnungen erfolgen in den Spalten F bis P.
Es werden nur die ersten Zahlen der Blöcke berechnet. Die weiteren Zahlen im Block können dann durch Addition der Gesamtzahl ermittelt werden. Das geschieht in den einzelnen Quadraten durch entsprechende Formeln.
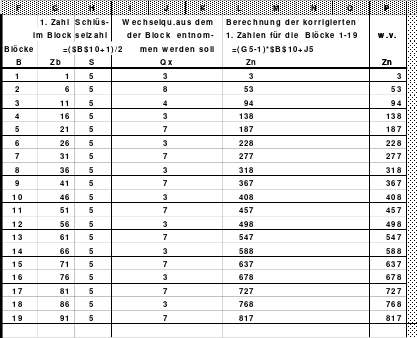
Die Formeln für die Berechnung sind:
Zb = 1. Zahl des Blockes im Basisquadrat =(F5-1) *$B$7+1 (gilt für Zeile 5)
S = Schlüsselzahl =($B$10+1) /2
Qx = Wechselquadrat aus dem der Block
entnommen werden soll - für die
1. Zahl im korrigierten Quadrat (Zelle J5) =B13
2. Zahl im korrigierten Quadrat (Zelle J6) =WENN((H6>B13); B13+H6; B13-H6+12
3. Zahl im korrigierten Quadrat (Zelle J7) = H7*3-J5-J6
4. Zahl im korrigierten Quadrat (Zelle J8) =$B$13
5. Zahl im korrigierten Quadrat (Zelle J9) =$B$10+1-$B$13
(weiter im ständigen Wechsel)
18. Zahl im korrigierten Quadrat (Zelle J22) =$B$13
19. Zahl im korrigierten Quadrat (Zelle J23) =$B$10+1-$B$13
Zn = Korrigierte 1. Zahl für die Blöcke 1 - 19,
(Zellen L und P) =(G5-1) *$B$10+J5 (gilt für Zeile 5)
Die Übernahme der berechneten Werte aus Spalte P in die Quadrate ist schwieriger als gedacht. Es gibt keine einheitliche Formel dafür. Zwar kann die Zeile aus der die Zahl entnommen werden soll berechnet werden, aber Mag fand keine Möglichkeit diese mit der Spaltenbezeichnung P zum kompletten Zellennamen (z. B. P5) zu verbinden. Die Folge war, dass er jede Zelle in den Quadraten einzeln programmieren musste. Diese Arbeitsweise führte mit zunehmender Quadratgröße zur Häufung von Fehlern. Um die Fehlerquote zu senken und die Arbeit übersichtlicher zu gestalten, erstellte Mag ein Hilfsprogramm, das vollkommen ab Zelle S31 zu finden ist.
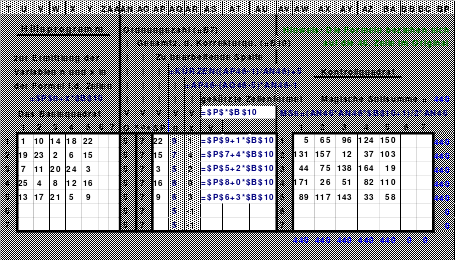
Im linken Bereich wird das Basisquadrat eingegeben, im Beispiel das Springerquadrat der 5. Ordnung.
Im mittleren Bereich erfolgt die Berechnung.
Die Formel für die Zellen ist =$P$n+x*$B$10 wobei n und x berechnet werden müssen. Dazu wird in die Zelle AN46 die Ordnungszahl eingegeben. Die Eingabe in den nächsten Zeilen erfolgt programmiert. Das Gleiche gilt für Zelle AQ46 in die die Gesamtzahl der Korrekturquadrate eingegeben wird.
Wird in die Spalte AP eine Spalte des Basisquadrates eingegeben, erfolgt aufgrund der angegebenen Formeln sofort die Berechnung von n und x.
In der Zelle AS44 ist die Formel =$P$n+x*$B$10 durch Herausnahme des Teiles n+x gekürzt und durch vorsetzen des Textzeichens (“) umgewandelt zu “=$P$*$B$10. Diese Formel wird unverändert in die erforderlichen Zellen der Spalte AS kopiert. Anschließend werden die Werte n+x in die Formeln eingeschrieben. Ist das erfolgt, so werden sofort die Zahlenwerte berechnet und angezeigt.
Die Zahlenwerte bzw. Formeln werden in den Kontrollbereich übernommen. Durch Vergleich der Summe mit der magischen Sollsumme kann die Richtigkeit des Ergebnisses festgestellt werden. Nachdem so alle Spalten bearbeitet wurden, kann das berechnete Quadrat in das entsprechende Quadrat in der Hauptdatei kopiert werden.
Sicherlich gibt es eine einfachere Möglichkeit. Aber Mag hat bereits betont, dass er kein Informatiker ist. Sollten Sie das Problem besser lösen, würde es Mag freuen.
7.3.3. Korrekturquadrate (Excel)
Die Datei
„Korrekturquadrate“
ist ein Excel-Programm, das nicht im Internet geöffnet werden kann. Um das Programm zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
7.4.Wechselquadrate
7.4.1. Erläuterungen zur Bildung von Wechselquadraten
In den Ausführungen von Mag wurde mehrmals der Einsatz von Wechselquadraten gefordert. Die Datei “Korrekturquadrate” baut fast ausschließlich auf Wechselquadraten auf.
Bei Wechselquadraten werden die Zahlen abwechselnd von links nach rechts in die zu bildenden Wechselquadrate eingetragen. Das ist am Beispiel zu erkennen.
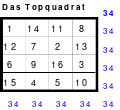
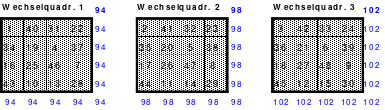
Weiter zeigt sich, dass die Zahlen innerhalb der Quadrate eine Differenz von 3 haben, was der Anzahl der Wechselquadrate entspricht.
Wechselquadrate können aus allen Basisquadraten gebildet werden, egal ob gerade oder ungerade Quadrate.
Aus all diesen Regeln hat Mag eine Formel abgeleitet, mit der die einzelnen Wechselquadrate berechnet werden können.
Diese Formel ist: Zn=Za*WQg-WQg+WQx oder auch Zn=(Za-1) *WQg+WQx
Darin bedeuten: Zn = Die neue Zellenzahl im Quadrat WQx
Za = Die Zellenzahl im Basisquadrat
WQg = Anzahl der zu bildenden Wechselquadrate
WQx = Das aktuell zu berechnende Wechselquadrat
Damit war auch die Möglichkeit vorhanden, die Berechnungen mit dem Computer vorzunehmen, was Mag mit der Datei “Wechselquadrate.xls” auch realisierte.
Auf der nächsten Seite ist die Datei stark reduziert dargestellt. Im Original ist die Bildung von Wechselquadrate bis zur Größe der 18. Ordnung möglich. Die Datei untergliedert sich in den Eingabebereich und den Ausgabebereich. Im Eingabebereich wird das zu pendelnde Basisquadrat eingegeben oder einkopiert.
Weiter ist die Anzahl der zu bildenden Wechselquadrate in Zelle D9 festzulegen. Nach Eintrag des aktuell zu bildenden Wechselquadrates in Zelle D14 wird das berechnete Quadrat im Ausgabebereich ausgegeben.
In der Abbildung wurde von 4 auszugebenden Quadraten gerade das 3. berechnet. Mit diesem Beispiel werden die genannten Regeln bestätigt.
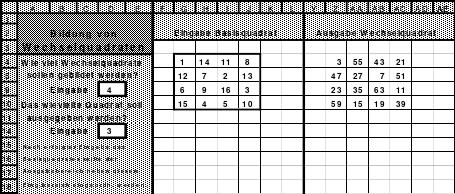
Die Formel für die Berechnung der neuen Zellenzahlen ist:
=WENN((F3>0); F3*$D$9-$D$9+$D$14;””)
Diese Formel wurde in die Zelle Y3 eingegeben und von dort in alle Zellen des Ausgabebereiches kopiert.
7.4.2. Wechselquadrate (Excel)
Die Datei
„Wechselquadrate“
ist ein Excel-Programm, das nicht im Internet geöffnet werden kann. Um das Programm zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
7.5. Multiquadrate
7.6.1. Erläuterungen zu den Multiquadraten
Im Abschnitt “Hexen 1 x 1” wurde die Multimethode ausführlich beschrieben.
Die von Mag erstellte Datei ”Multiquadrate.xls” ermöglicht die Berechnung solcher Multiquadrate mittels Computer.
Mit ihr können Multiquadrate von der 4. bis zur 13. Ordnung berechnet werden. Die Eingaben erfolgen im linken Eingabebereich für die gewählte Quadratgröße und die magische Summe, die das Quadrat haben soll. Beide Eingaben werden geprüft und mit “o.k.” bestätigt, oder mit “Fehler” verworfen. Ein Fehler besteht, wenn die angezeigten Größenordnungen nicht eingehalten werden.
Nach erfolgten Eingaben wird das gewünschte Quadrat berechnet und ausgegeben. Im Beispiel ist es ein Quadrat der 5. Ordnung, dass eine magische Summe von 123 haben soll. Das gewünschte Quadrat sollte durch Teilung unmittelbar neben den Eingabebereich eingeordnet werden, was übersichtlicher ist.
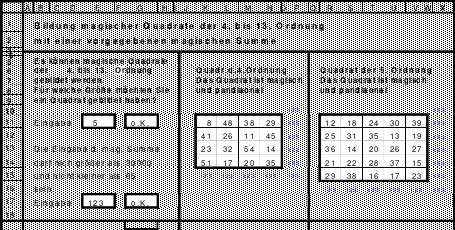
Aus Sicherheitsgründen ist die Datei, außer den beiden Eingabezellen, schreibgeschützt.
Erweiterte Erläuterungen für Fans
Im Abschnitt “Hexen 1 x 1” wurde die Multimethode ausführlich beschrieben. Hier nochmals diese Methode in Kurzfassung:
Ein magisches Basisquadrat beliebiger Größe wird vorwiegend durch Multiplikation der Zellenzahlen mit einem Faktor so vergrößert, dass sie einer vorgegebenen magischen Summe entsprechen.
Dazu ist die Vorgabesumme durch die magische Summe des gewünschten Basisquadrates zu teilen und man erhält den Faktor, mit dem alle Zellenzahlen des Basisquadrates zu multiplizieren sind.
In der Regel bleibt nach der Teilung noch ein Rest, der auf die nach der Multiplikation berechneten Zellenzahlen anteilig zugeschlagen werden muss. Dieser Summand wird durch Division des Restes durch die Ordnungszahl berechnet. Wenn dann noch ein so genannter Endrest übrig bleibt, muss dieser im Quadrat so in einzelne Zellen zugeschlagen werden, dass dieser in allen Reihen einmal wirksam wird.
Diese Berechnungen erfolgen für alle Quadrate einheitlich, was die Bildung der Datei ”2.Multiquadrate.xls” zur Berechnung von Multiquadraten ermöglichte..
Mit ihr Können Multiquadrate von der 4. bis zur 13. Ordnung berechnet werden. Die Eingaben erfolgen im linken Eingabebereich für die gewählte Quadratgröße und die magische Summe, die das Quadrat haben soll. Beide Eingaben werden geprüft und mit “o.k.” bestätigt, oder mit “Fehler” verworfen. Bei der Ordnungszahl wird geprüft, ob die Eingabe >3 und <14 ist. Die gewünschte Summe wird geprüft, ob die maximal zulässige Summe überschritten, oder die Mindestsumme unterschritten wird. Dabei entspricht die Mindestsumme der magischen Summe des Basisquadrates. Die maximale Summe sichert, dass unter Beachtung der Zellenbreite, die Zahlen numerisch angezeigt werden und keine Rautenbildung erfolgt. Die Berechnungen der Mindest- und der Maximalsumme erfolgt in den ausgeblendeten Bereich der Zeilen 22 bis 46 und den Spalten B bis H sowie DV bis DZ.
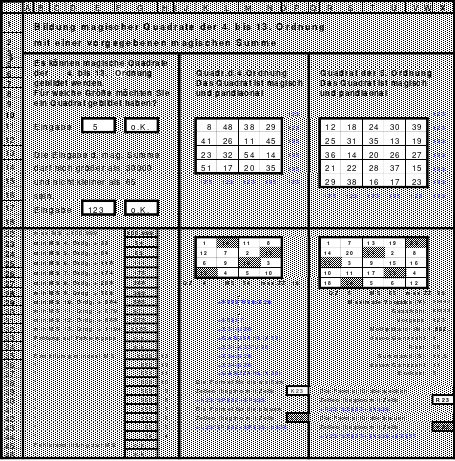
Die Berechnungen der Quadrate erfolgten unterhalb des jeweiligen Quadrates. Dort ist als erstes das Basisquadrat abgebildet, auf das bei den Berechnungen des Multiquadrates (im oberen Bereich) Bezug genommen wird. Hier wird auf die blau schattierten Zellen hingewiesen, in die der Endrest mit eingerechnet werden muss.
Darunter die Berechnungen des Multiplikators, des Restes und des Endrestes. Die Formeln für die Berechnung des Quadrates der 5. Ordnung wurden aus Platzgründen in den Berechnungsbereich des Quadrates der 4. Ordnung aufgenommen und bedürfen keiner weiteren Erklärungen.
Die unteren 2 Formeln im Berechnungsbereich des Quadrates der 5. Ordnung befinden sich im Textformat.
Die obere Formel gilt für alle weißen Zellen und wurde in die 1. Zelle der 1. Zeile kopiert. Dort erfolgte durch Löschung des Textzeichens die Umwandlung in ein numerisches Format. Von dort wurde sie in alle anderen Zellen des Quadrates kopiert.
Gleiches erfolgte mit der unteren Formel, die für die Zellen bestimmt ist, denen der Endrest zugeschlagen werden soll. Diese wird im Beispiel in die Zelle V11 des oberen Quadrates kopiert und nach Umwandlung in ein numerisches Format in alle Zellen kopiert, die den blau markierten Zellen im unteren Quadrat entsprechen. Die Zelle V11 ist die Zelle, die sich in der Formel auf die Zelle V23, eine blau markierte, bezieht.
7.5.2. Multiquadrate (Excel)
Die Datei
„Multiquadrate“
ist ein Excel-Programm, das nicht im Internet geöffnet werden kann. Um das Programm zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
7.6. Multiwürfel
7.6.1. Erläuterungen zum Multiwürfel
Mit dem Excel-Programm “Multiwürfel” können teilmagischer Würfel der 4. Ordnung gebildet werden. deren magische Summen von 130 bis 20.000 groß sein können.
Den Programmnamen “Multiwürfel” hat Mag gewählt, weil die teilmagischen Würfel einmal vorwiegend durch Multiplikation gebildet werden und zum anderen die vorgegebenen magischen Summen vielfältig, von 130 bis 20.000, groß sein können. Die vom Computer errechneten Würfel sind nur teilmagisch, denn alle Zahlenreihen der möglichen 12 Quadrate der 4. Ordnung haben die Vorgabe als Summe, jedoch nicht die Diagonalen, dafür aber die 4 großen Würfeldiagonalen!
Es ist wissenschaftlich bewiesen, dass die Bildung eines vollkommen magischen Würfels der 4. Ordnung nicht möglich ist.
Der Basiswürfel für die Berechnung der Multiwürfel ist ein teilmagischer Würfel mit den Zahlen von 1 bis 64. Diesen hatte Mag vor Jahren konstruiert, um zu prüfen, ob die Bildung eines vollkommenen magischen Würfels der 4. Ordnung nicht doch möglich ist. Es war ihm nicht gelungen. Er hatte jedoch einige teilmagische Würfel gefunden. Davon auch den hier eingesetzten Würfel, bei dem von den Diagonalen nur die großen Würfeldiagonalen der magischen Summe entsprechen.
Das Programm ist in 5 Bereiche untergliedert:
1. Der Eingabebereich
2. Ausgabebereich des berechneten Würfels mit farbiger Gestaltung der 4
waagerechten Quadrate.
3. Wie 2., jedoch mit 4 senkrechten Quadraten.
4. Darstellung der großen Würfeldiagonalen.
5. Die Berechnungen
Aus Sicherheitsgründen ist das Programm schreibgeschützt. Lediglich die Zelle für die Eingabe der gewünschten magischen Summe nicht.
Aus gleichem Grund wurde der Bereich der Berechnungen, mit den Zeilen 26 bis 52, ausgeblendet.
Anwendung
In die gekennzeichnete Zelle C14 ist die gewünschte magische Summe einzugeben. Alle Zahlen von 130 bis 20.000 sind zulässig. Fehlerhafte Eingaben werden angezeigt und alle Zahlen des Würfels mit Null belegt. Ist die Eingabe in Ordnung, wird der teilmagische Würfel sofort in den Ausgabebereichen 2, 3 und 4 ausgegeben. Alle Zahlenreihen, außer den Diagonalen der einzelnen Quadrate, haben die vorgegebene magische Summe. Auch die 4 großen Würfeldiagonalen.
Speziell für Fans --- Der Lösungsweg
Zum besseren Verständnis werden die einzelnen Zahlenreihen in waagerechte, schräge (nicht diagonale) und senkrechte Reihen untergliedert. (siehe dazu die Würfelabbildung im Programm). Hinzu kommen noch die großen Würfeldiagonalen. Die kleinen Diagonalen sind die der einzelnen Quadrate. Da diese nicht die magische Summe haben, werden sie kaum genannt.
Der Basiswürfel enthält alle Zahlen von 1 bis 64. Die magische Summe beträgt 130.
Nun zu den Rechenschritten
Als erstes wird die vorgegebene magische Summe durch die magische Summe des Basiswürfels (=130) dividiert und man erhält den Multiplikator und einen Rest. Alle Zahlen des Würfels, von 1 bis 64, werden im 1. Schritt mit dem Multiplikator multipliziert.
Nun muss der Rest auf die Zeilen und Spalten aufgeteilt werden. Der Rest wird durch die Ordnungszahl geteilt und man erhält den Summanden und einen Endrest. Im 2. Schritt werden alle Zellen um den Summanden erhöht.
Der Endrest ist immer kleiner als die Ordnungszahl und darf im 3. und letzten Schritt nur einmal jeder Spalte, Zeile und im Normalfall auch den Diagonalen zugeschlagen werden.
Bei den Multiquadraten ist dieses Problem leicht zu lösen, nicht aber bei einem Würfel. Mag hat das Problem gelöst. Wer wissen will, welchen Zellen der Endrest zugeschlagen wird, der gibt als Vorgabe 1301 ein. Alle Zahlen enden dann mit einer Null (0) als letzte Ziffer, die gesuchten jedoch mit einer 1.
Die Berechnungen befinden sich in den Spalten A bis H und Zeilen 26 bis 52.
Der Multiplikator ist in der Zelle F33, der Summand in Zelle F36 und der Endrest in Zelle F37 zu finden.
Daraus hat Mag die Formeln für die einzelnen Zellen gebildet:
1. Formel für alle Zellen: “=(M32*$F$33) +$F$36
2. Formel für Zellen mit Endrest: “=(M32*$F$33) +$F$36+$F$37
Die Formeln hat Mag zuerst in die Zelle M2 eingegeben!
Diese sind im Textformat und müssen in der Zelle M2 durch Löschen des Textzeichens (“) in ein Zahlenformat umgewandelt werden. Von dort können sie dann in die Zellen des Würfels kopiert werden.
Zuerst hat Mag die Formel 1 in alle Zellen des Würfels kopiert und anschließend die Formel 2 in die Zellen, denen der Endrest zugeschlagen werden muss.
Es ist noch eine Frage offen. Die nach dem Basiswürfel. Der kann angesehen werden durch Eingabe von 130, der magischen Summe des Basiswürfels. Dann wird der Basiswürfel mit den Zahlen von 1 bis 64 angezeigt.
Der Basiswürfel
Sicher wird auch gefragt, wie der Würfel der 4. Ordnung gebildet wurde.
Der Lösung gingen viele Versuche und Analysen voraus. Dabei konnte auch die nachfolgende Variante gefunden werden. Der Würfel ist nur teilmagisch. Alle Quadrate haben Zeilen und Spalten mit der richtigen magischen Summe von 130. Nicht aber deren Diagonalen. Dafür haben die Hauptdiagonalen des Würfels die richtige magische Summe von 130. Mag hat dieser Lösung den Vorzug gegeben. Er hat keine weiteren Untersuchungen unternommen um einen vollkommen magischen Würfel der 4. Ordnung zu finden, denn es soll wissenschaftlich bewiesen sein, dass es keinen 100%ig magischen Würfel der 4. Ordnung geben kann.
Nachdem Mag 4 Pendelquadrate des Topquadrates gebildet hatte, konnte er feststellen, dass auch die Duos der gependelten Quadrate die einheitliche Summe von 65, der halben magischen Summe, haben.
In den Quattros sind die Summen der Zeilen mit 73 und 57, sowie die der Spalten mit 49 und 81 gleich. Das bedeutet, dass diese nach bestimmten Regeln austauschbar sind.
Setzt man die Quadrate in der Folge 1, 4, 3 und 2 übereinander, stimmen die großen Hauptdiagonalen und auch die kleinen Diagonalen in den Quadraten. Sie haben die Summe von 130. Außer den 4 Quadraten sind jedoch alle senkrechten Quadrate nicht magisch, selbst halbmagisch sind sie nicht.
Es galt, die Quadrate so zu verändern, dass dieser Mangel aufgehoben wird. Das erreichte Mag durch das Wenden der einzelnen Quattros um die blauen Linien.
Die so entstandenen Quadrate sind nach wie vor magisch. Eine Anordnung mit dem Ziel, 130 als Summe für die senkrechten Reihen und für die Hauptdiagonalen zu finden, schlug fehl.
Eine Neuordnung der Quadrate wurde unumgänglich. Dazu wurden die einzelnen Quattros untereinander angeordnet und anschließend zu neuen Quadraten zusammengefügt. Dabei bildeten die Quattros gleicher Farben die neuen Quadrate. Die Zusammensetzung erfolgte so, dass die Quattros der Spalte 2 unter die Quattros aus Spalte 1, die der Spalte 3 rechts von den Quattros aus Spalte 1 und die Quattros der Spalte 4 in die noch offenen Stellen kamen.
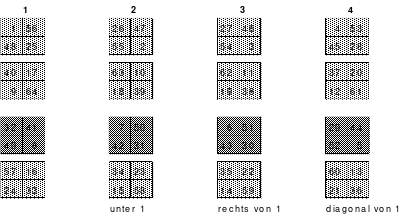
Das Ergebnis sind die 4 Quadrate in den Farben blau, grün gelb und rot. Die Summen der Zeilen und der Spalten dieser sind einheitlich 130, nicht aber die Diagonalen, weshalb diese Quadrate nur halbmagisch sind.
Werden die Quadrate übereinandergesetzt, so sind auch die senkrechten Zahlenreihen 130 groß, z. B. 1+40+32+57=130, oder 54+19+43+14=130. Damit sind auch alle anderen Quadrate im Würfel halbmagische Quadrate.
Die großen Diagonalen haben die richtige Summe von 130.
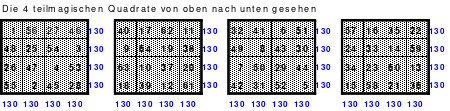
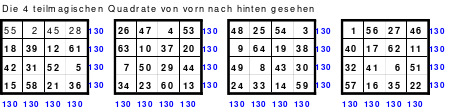
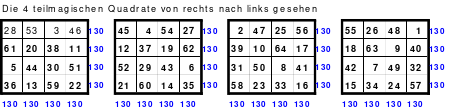
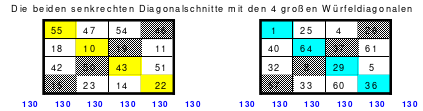
Der so gebildete halbmagische Würfel ist in die Excel-Datei “Multiwürfel” übernommen worden.
7.6.2. Multiwürfel (Excel)
Die Datei
„Multiwürfel“
ist ein Excel-Programm, das nicht im Internet geöffnet werden kann. Um das Programm zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
8.Schlusswort
8.1. Schlusswort
“Allen Menschen recht getan, ist eine Kunst, die niemand kann.”
Auch Mag kann das nicht und ist sich sicher, dass die Meinungen zu seinem Buch sehr unterschiedlich sein werden. Sie werden von zu ausführlich bis zu kurz erläutert, von zu einfach bis zu schwer machbar, von bekannt bis zu unbekannt, usw. usw. reichen.
Mag hat für all diese Meinungen Verständnis. Sie ergeben sich aus den persönlichen Kenntnissen über die magischen Quadrate. Diese reichen von unbekannt bis zu einem hohen Wissen und Mag hat eben deshalb versucht für jeden etwas zu bringen. Er will Neulingen mit dem interessanten Gebiet der magischen Quadrate vertraut machen, aber auch den erfahrenen Fans Neues bieten. Mag ist überzeugt, dass einiges davon in seinen Ausführungen zu finden ist. Er denkt dabei an seine Excel-Programme, insbesondere an das “Kontrollquadrat” und die “Korrekturquadrate”, die viel Kleinarbeit abnehmen.
Auch im “Hexen 1x1” wird mancher Fan Neues entdecken. Das könnte z. B, die Lösung “Einfach Clever”, die “Königsquadrate”, die “Primzahlenquadrate”, dass “Austauschquadrat” oder das “Meisterquadrat” sein. Das wird je nach Kenntnissen und Fähigkeiten jedes Einzelnen unterschiedlich sein.
Gerade die letztgenannten werden für Anfänger möglicherweise schwer verständlich sein, was sich aber mit steigendem Kenntnisstand verändern wird. Mag möchte diesen Interessenten Mut machen, nicht zu zeitig die Beschäftigung mit den magischen Quadraten aufzugeben.
Die Ausführungen im Hexen 1 x 1 wurden in der Art und Weise einer Vorführung gemacht. Das war des besseren Verständnisses wegen so gewollt. Es bedeutet aber nicht, dass diese Ausführungen ausschließlich für Darbietungen gedacht sind. Sie sollen eher Anregungen sein, sich auch mit dieser Seite der magischen Quadrate zu beschäftigen. Das betrifft insbesondere auf die Lösungen mit Quadraten der 7. 8. und 9. Ordnung zu.
Mag möchte an seine Worte, zu den nur begrenzt möglichen Vorführungen, die er im Vorwort gemacht hat, erinnern.
Mag ist sich im Klaren, dass das vorliegende Buch durch eine Überarbeitung effektiver gestaltet werden kann. Aus Altersgründen kann er selbst diese Aufgabe nicht mehr realisieren und würde es begrüßen, wenn sich dazu ein Fan verpflichtet fühlen sollte. Mag gibt dazu seine Zustimmung, ohne irgendwelche Rechtsansprüche geltend zu machen.
Viel Freude und Spaß bei der Beschäftigung mit magischen Quadraten wünscht Ihnen
Mag Quadra
9.Anhang
9.1. Quadratparade (Excel)
Die Datei
„Quadratparade“
ist eine Excel-Datei, die nicht im Internet geöffnet werden kann. Um die Datei zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
9.1.1. Ausgewählte Quadratkombinationen und andere Kuriositäten
Nachfolgend werden Original-Ausschnitte aus der Exceldatei “Ausgewählte Quadratkombinationen und andere Kuriositäten” gezeigt.
Die Excel-Datei ist im Anhang unter 9.2.2. zu finden. Diese enthält weitere Darstellungen und ausführliche Erläuterungen der Lösungen.
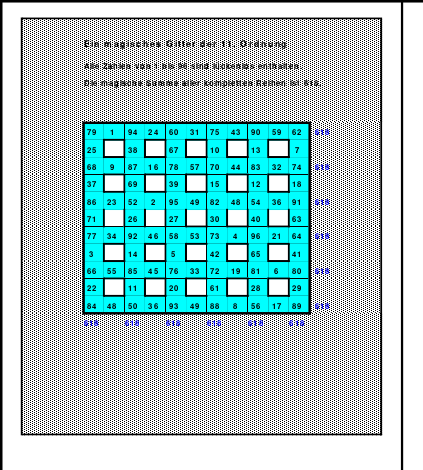
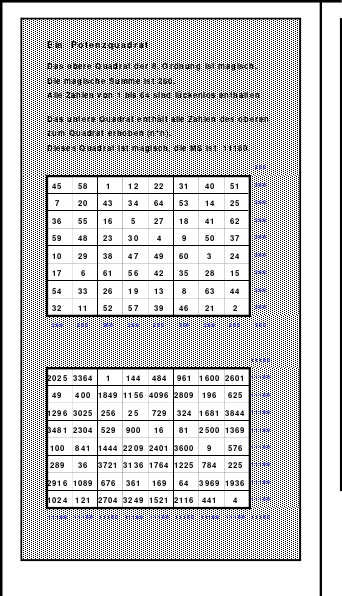
9.2.2. Ausgewählte Kombiquadrate (Excel)
Die Datei
„Ausgewählte Kombiquadrate“
ist eine Excel-Datei, die nicht im Internet geöffnet werden kann. Um die Datei zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
9.3. Das Monsterquadrat
Als Mag die erste Datei zur Bildung von Pendelquadraten erstellt hatte, war das größte bisher erstellte magische Quadrat ein magisches Quadrat der 3001. Ordnung. Dieses Quadrat wurde in das Guinnessbuch der Rekorde aufgenommen. Obwohl Mag seine Zweifel über den Sinn solcher Riesenquadrate geäußert hat, reizte ihn die Erarbeitung eines noch größeren Quadrates. Dabei wollte Mag keinen Eintrag in das Guinnessbuch der Rekorde anstreben, sondern zeigen, dass die Bildung eines Riesenquadrates auf der Grundlage der bisher erworbenen Kenntnisse ohne besondere Schwierigkeiten machbar ist. Gleichzeitig wollte Mag die Leistungsfähigkeit seiner erstellten (Works-)Excel-Anwendungen, insbesondere von “Pendelquadrate”, das Mag zur Bildung von Pendelquadraten ausgearbeitet hat, unter Beweis stellen.
Ein Ausschnitt aus dem Monsterquadrat
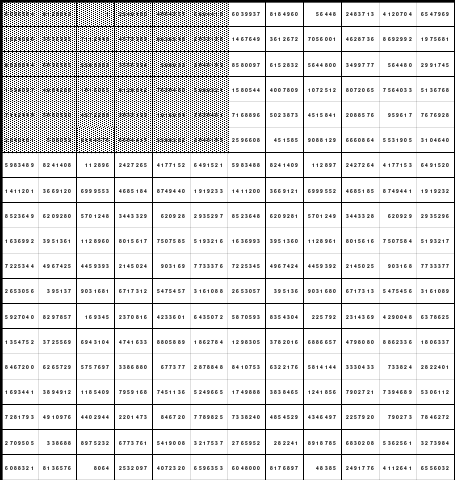
Als kleinstes Quadrat wählte Mag das Hexaquadrat, ein Quadrat der 6. Ordnung.
Das Monsterquadrat setzt sich aus 254016 magischen Quadraten der 6. Ordnung zusammen. Die magischen Summen dieser 6er Quadrate sind mit 27.433.731 alle gleich. Besonders möchte Mag auf das 1. gependelte 6er Quadrat, oben, links, im Monsterquadrat aufmerksam machen. Es ist grün schattiert. Blau schattiert sind die kleinste Zahl 1 und die größte Zahl 9.144.576.
Die Vielzahl der möglichen Teilquadrate im Monsterquadrat der 3024. Ordnung sind 24 verschiedene Quadrate mit Ordnungszahlen von 6 bis 3024
Das Gesamtquadrat hat die magische Summe von 13.826.600.424 (> 13,8 Mrd.) und enthält alle Zahlen von 1 bis 9.144.576 lückenlos und nur einmal.
Das Quadrat entstand durch das Pendeln des 6er Quadrates. Natürlich hat Mag das Hexaquadrat nicht 254.016-mal gependelt. Das wäre ein nicht zu bewältigender Aufwand. Mag hat deshalb eine rationelle Lösung angewendet. Er wählte als Ausgangsquadrat ein Quadrat der 18. Ordnung, dass er aus 9 gependelten Quadraten der 6. Ordnung bildete. Um das Gesamtquadrat der 3024. Ordnung aus 18er Quadraten zu bilden, sind in der Reihe 168 dieser Quadrate erforderlich und für das Gesamtquadrat 28224.
Mag schaffte die Berechnung aller Teilquadrate einschließlich deren Einordnung in die 12 Teilabschnitte des Gesamtquadrates in nur 6 Stunden.
Zur Berechnung aller Zahlen für das Monsterquadrat hat Mag die von ihm erstellt Datei “Pendelquadrate” genutzt. Als erstes pendelte er das 6er Hexaquadrat 9-fach und stellte es zu einem Quadrat der 18. Ordnung zusammen. Dieses Quadrat pendelte er 7-fach. Die so erhaltenen 7 Quadrate speicherte er untereinander. Es war ein Zahlenpaket mit 18 Spalten und 126 Zeilen entstanden. Dieses Zahlenpaket pendelte Mag anschießend 6-mal und setzte die 6 Zahlenpakete ebenfalls untereinander und erhielt so ein Zahlenpaket von nunmehr 18 Spalten und 756 Zeilen. Dieses Zahlenpaket pendelte Mag nochmals 4-fach und erhielt so 18 Spalten mit 3024 Zeilen.
Das letztgenannte Zahlenpaket mit 18 Spalten musste in der weiteren Folge 168-fach gependelt werden um so die gesamte Anzahl von 3024 Spalten zu erhalten. Wegen der großen Spaltenanzahl musste das Monsterquadrat in 12 Datenbanken eingeordnet werden.
Schlussbemerkungen
Diese Ausführungen entstanden vor Jahren mittels der damaligen Standard-Software Works. Diese sind auch ohne Anpassung an Excel verständlich, weshalb Mag eine solche nicht für erforderlich hält.
Das erwähnte Rekordquadrat der 3001. Ordnung ist bereits überholt. Auch Mag´s Monsterquadrat der 3024. Ordnung.
9.4.1. Primzahlen-Rahmenquadrat der 32. Ordnung (Ausschnitt)
Mit der magischen Summe von 797 440 
Das Gesamtquadrat kann im Anhang als Excel-Datei unter 9.4.2. eingesehen werden.
9.4.2. Primzahlen Rahmenquadrat (Excel)
Die Datei
„Primzahlen Rahmenquadrat“
ist eine Excel-Datei, die nicht im Internet geöffnet werden kann. Um die Datei zu nutzen ist ein Herunterladen auf Ihren PC erforderlich.
Voraussetzung ist eine vorhandene Installierung von Excel auf Ihrem PC.
Downloaden
9.4.3. Das Primzahlen-Rahmenquadrat der 32. Ordnung
Für die Bildung des Primzahlen-Rahmenquadrat hat Mag zur Optimierung alle Primzahlen bis 50000 einbezogen. Der Mittelwert beträgt damit 25000 und ein magisches Quadrat der 4. Ordnung müsste eine magische Summe von rd. 4 x 25000 = 100000 haben. Dementsprechend hat Mag die aufgeführten Primzahlenreihen für das Quadrat ausgewählt, dass eine magische Summe von 99680 hat. Daraus ergeben sich ein Mittelwert von 24920, die Duosumme von 49840 und 223 als größte Primzahl die für die Selektierung der Primzahlen, die als Ergänzungszahlen der Duos infrage kommen.
Auf der Grundlage dieser Werte können nun die Duos ermittelt werden. Dazu hat Mag eine Datenbank unter WORKS eingerichtet. In das Feld a hat Mag alle 2937 Primzahlen die kleiner als der Mittelwert sind aus der Primzahlenliste übernommen. Im Feld b wurden mittels der Formel =49840-a die Ergänzungszahlen für die Duos gebildet. Alle Zahlenpaare a/b sind Duos mit der Summe von 49840. Jedoch sind die berechneten 2. Zahlen nur selten eine Primzahl. Deshalb müssen alle Duos, bei denen nicht beide Zahlen Primzahlen sind ausgeschlossen werden. Da die 1. Zahl eine Primzahl ist, müssen nur die Ergänzungszahlen überprüft werden. Diese Selektion erfolgt genauso, wie bei der Ermittlung der Primzahlen durch das Siebverfahren. Dies erfolgt mit der Formel =WENN(UND(b/d>0; GANZZAHL(b/d) =b/d; b/d<>1);"„; b), die in das Feld c eingegeben wurde. In das Feld d werden nacheinander alle 51 Primzahlen von 3 bis 233 eingegeben (z.B. =3). Alle Zahlen, die mehrzahlig durch die eingegebenen Primzahlen teilbar sind, werden nicht in das Feld c übernommen. Nach jeder Primzahleneingabe in das Feld d werden immer alle Zahlen aus c nach b kopiert. Nach der Eingabe von =233 sind alle Ergänzungszahlen gelöscht, die keine Primzahlen sind. Zur besseren Übersicht hat Mag die gelöschten Ergänzungszahlen in grauer Schrift belassen.
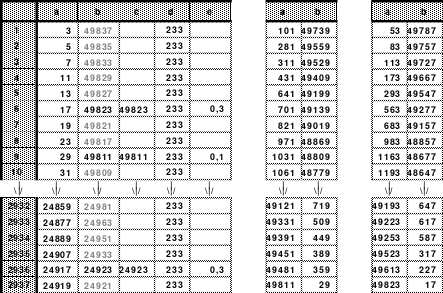
Um die verbliebenen Duos zusammenzufassen und gleichzeitig auch zu sortieren hat Mag in das Feld e die Formel =b/10-GANZZAHL(b/10) eingegeben. Alle Zahlen mit der 9 als letzte Ziffer werden im Feld e durch den Wert 0,9 gekennzeichnet. Analog mit 0,7 0,3 und 0,1 die Zahlen mit den Endziffern 7, 3 und 1.
Durch das absteigende Sortieren des Feldes e werden die Duos hintereinander in 4 Gruppe ausgewiesen. Das sind die Gruppen ...1/...9, ...3/...7, ...7/...3 und ...9/...1. Diese Gruppen sollten in einer Kalkulationstabelle zwischengespeichert werden, um diese eventuell anders zusammenzustellen. So wie Mag die 539 Duos in der folgenden Übersicht in nur die beiden Gruppen ...1/...9 und ...3/..7 ausweist.
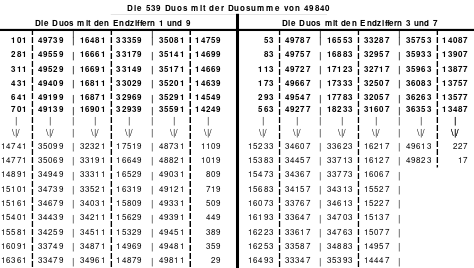
Bitte haben Sie Verständnis, wenn Mag nicht alle Duos, sondern nur einen Ausschnitt zeigt. Die Primzahlenduos haben nämlich keine allgemeine Gültigkeit, sondern müssen für jedes Quadrat neu erstellt werden, weil deren Duosumme aus dem jeweiligen Mittelwert berechnet wird. Deutlich wird dies besonders bei der Aufstellung ungerader Primzahlenquadrate. Hier entfallen in Abhängigkeit der letzten Ziffer der Duosumme immer Primzahlen mit einer bestimmten letzten Ziffer, weil bei ungeraden Quadraten die Duosumme niemals die Endziffer 0 aufweisen kann. Aus diesem Grund ist beim Aufbau eines geraden Schachtelquadrates auch eine mit 0 endende Duosumme anzustreben.
Mittels der gefundenen Duos können die Rahmen nacheinander gebildet werden. Mag hat aus den 539 Duos alle Rahmen vom 6er bis 32er gestaltet. Übrig blieben gerade mal 35 Duos, aus denen kein 34er Rahmen mehr gebildet werden kann. Damit hat Mag das aus den Primzahlen bis 50000 herauszuholende Optimum erreicht. Nachstehend eine Übersicht der im XXL-Schachtelquadrat vereinten Quadrate.
Mag möchte diesen Abschnitt nicht beenden, ohne noch ein paar Tipps zur Arbeit bei der Bildung der Rahmen zu geben. Aus Platzgründen erfolgen diese Beschreibungen jedoch nur an einem Schachtelquadrat der 10. Ordnung. Es entspricht aber dem Teilquadrat der 10. Ordnung im XXL-Schachtelquadrat. Zum Einsatz kommt dabei eine Kalkulationstabelle.
Das Kernquadrat hat die magische Summe von 99680. Die umgebenden Rahmen sind jeweils um die Duosumme größer. Der 6er Rahmen muss als Reihensumme 149520 haben, der 8. die Summe 1993360 und der 10er Rahmen 249200. Diese Werte werden den Spalten und Zeilen jeweils als negativer Wert vorangestellt, so wie es die blauen Zahlen zeigen. Mittel der Autosummierung werden die Summen für die Zeilen und Spalten errechnet. Die dabei entstehenden Summen sind grün dargestellt. (Natürlich muss die Summenbildung vor der Rahmengestaltung erfolgen.)
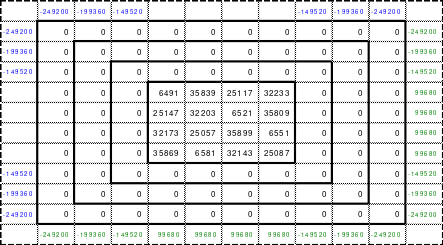
Nach der Bildung des 6er und 8er Rahmens soll nun der 10er Rahmen entstehen. Dazu wird die Datei geteilt. Dabei sind nur die obere und untere Zeile des 10er Rahmen von Bedeutung. Zur besseren Orientierung kann der vorherige Rahmen noch mit dargestellt werden. Durch diese Teilung kann der linke Bereich nach rechts und links bewegt werden, wobei die Zeilensumme im rechten Teil stets sichtbar bleibt. Das ist besonders für große Rahmen, wie der 32er sehr wichtig.
Die Liste der Duos wird als 2. Datei geöffnet und unter den gezeigten Ausschnitt eingeordnet.
Als erstes werden die Eckzellen mit Duos belegt. Dann wird jeweils eine Zahl der Duos in die obere Zeile durch Kopierung eingetragen. Nach jeder Eintragung erfolgt sofort und automatisch die Neuberechnung der Summe und es kann der fehlende Betrag abgelesen werden. Die 4. und 3.-letzten Zahlen sollten dabei so gewählt werden, dass ein Rest annähernd in der Größe der Duosumme verbleibt, weil dann die restlichen Zahlen günstiger gefunden werden. Wenn Sie die grauen Zahlen nicht beachten, so müssen die letzten beiden Zahlen den Rest von 66820 ergeben. Mag hat sich für Duozahlen mit der Endziffer 1/9 entschieden. In die Zelle J2 werden nun nacheinander Duozahlen mit der Endziffer 9 eingegeben. Jedes Mal wird geprüft, ob es eine Duozahl gibt, die den Rest ausgleicht. Das war im Beispiel mit den Zahlen 49139 und 17681 der Fall. Die Zeilensumme war nach dem Eintrag dieser beiden Zahlen 0. Danach erfolgte das Einsetzen der anderen zu den Duos gehörenden Zahl in die untere Zeile. Damit waren die Zeilen mit der richtigen Summe von 249200 fertig gestellt.
Mit den Spalten wird anschließend analog verfahren. Diese werden natürlich senkrecht auf dem Monitor dargestellt.
Noch ein sehr wichtiger Hinweis! Bevor mit der Eintragung von Duos in die Rahmen begonnen wird, müssen alle Duos markiert werden von denen auch nur eine Zahl Bestandteil des Kernquadrates ist. Auch nach jedem Einsetzen einer Zahl in den Rahmen muss diese markiert werden. Nur so wird ausgeschlossen, dass Primzahlen im fertigen Quadrat doppelt vorhanden sind.
9.5. Perfektes Spiegelquadrat
Die Datei „Perfektes Spiegelquadrat“ ist eine Textdatei im Querformat und kann deshalb nicht hier eingeordnet werden.
Sie können die Datei gesondert aufrufen!
9.6. Der halbmagische Primzahlen-Würfel der 3. Ordnung
Mag hat gezeigt, dass die Arbeit mit Primzahlen bei der Bildung von magischen Quadraten, Polyquadraten und Anderem nahezu so umfangreich möglich ist, wie die Arbeit mit natürlichen Zahlen. Mag stellte sich deshalb die Aufgabe, auch einen magischen Würfel mit Primzahlen zu gestalten. Dabei begnügte er sich mit einem Würfel der 3. Ordnung. Magische Würfel der 3. Ordnung mit natürlichen Zahlen sind bekannt. Zum besseren Verständnis stellt Mag nachstehend einen solchen magischen Würfel der 3. Ordnung vor. Dieser ist teilmagisch, da nicht alle möglichen Quadrate der 3. Ordnung magisch sind, was mathematisch nachweisbar auch nicht erreich werden kann.
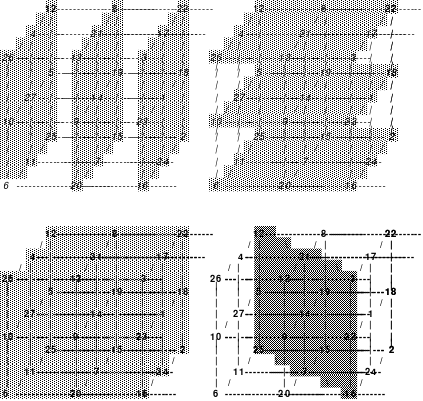
Dieser magische Würfel birgt eine Vielzahl von Überraschungen. So entsprechen die Summen aller Zahlenreihen, auch der Diagonalen, die die 14 in der Mitte durchlaufen der magischen Summe des Würfels von 42. Dazu zählen auch die 4 großen Würfeldiagonalen.
Diese sind: 12 + 14 + 16 = 42, 26 + 14 + 2 = 42, 3 + 14 + 25 = 42 und 22 + 14 + 6 = 42.
Damit sind auch die 3 Quadrate, die im Zentrum die 14 haben magisch, denn hier sind auch die Diagonalen 42 groß. Die 3 magischen Quadrate sind in den Abbildungen rot dargestellt.
Die übrigen 6 äußeren Quadrate (blau und grün) sind nur halbmagisch. Bei diesen entsprechen zwar alle Zeilen und Spalten der magischen Summe von 42, nicht aber deren Diagonalen.
Deshalb sind auch die 6 Quadrate, die durch diagonale Schnitte entstehen nicht magisch, sondern nur teilmagisch. Bei diesen Quadraten haben jeweils 3 Reihen (waagerecht oder senkrecht), 1 Reihe (senkrecht oder waagerecht) und die beiden Diagonalen die magische Summe. Sie sind deshalb nur teilmagisch. Unten rechts ist ein solches Quadrat gelb dargestellt. Hier entsprechen die Zahlenreihen 12 + 21 + 3 = 36 und 25 + 7 + 16 = 48 nicht der magischen Summe. Der Würfel enthält somit 3 magische, 6 halbmagische und 6 teilmagische Quadrate und ist folglich ein teilmagischer Würfel.
Ein perfekter magischer Würfel ist nachweisbar nicht möglich. Mag hat im Abschnitt ´Grundwissen´ herausgearbeitet, dass mehrere magische Quadrate der 3. Ordnung nur dann magisch und mit gleichen magischen Summen sein können, wenn alle die gleiche Zahl als mittlere Zahl haben. Das ist bei den äußeren 6 Quadraten jedoch unmöglich.
Aufbauend auf sein Grundwissen über die magischen Quadrate der 3. Ordnung hat Mag den magischen Würfel der 3. Ordnung analysiert und festgestellt, dass die einzelnen Quadrate voll und ganz den bekannten Regeln entsprechen. So sind in jedem Quadrat je 3 Zahlen von 1 bis 9, 10 bis 18 und 19 bis 27 zu finden. Bei den magischen Quadraten sind diese wie die Blöcke beim Miniquadrate eingeordnet. Die Differenzen der Zahlen innerhalb der Blöcke sind in jedem Quadrat gleich, ebenso die Differenzen von Block zu Block. So entspricht die Differenz zwischen den Zahlen innerhalb der Blöcke im waagerechten roten Quadrat 4 (Block 1 = 1; 5; 9, Block 2 = 10; 14; 18 und Block 3 = 19; 23; 27). Die Differenz zwischen den Blöcken beträgt 1 (9 zu 10 und 18 zu 19). Siehe dazu die Quadrate 1 und 2. Bei dem roten senkrechten Quadrat sind die Differenzen 1 und 4.
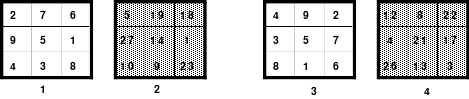
Nicht bei allen Quadraten des Würfels sind diese Regeln sofort erkennbar, was Mag anhand der Quadrate 3 und 4 beschreibt. Dabei ist das Quadrat 4 das oberste waagerechte. Das Quadrat 3 ist das Miniquadrat dem entsprechend die Einordnung der Zahlen erfolgte. Die Differenzen innerhalb der Blöcke sind einheitlich 9 groß. Im ersten Block 13 + 9 = 22; 22 + 9 = 31. Da aber nur die Zahlen bis 27 zur Verfügung stehen erfolgt durch Abzug von 27 eine Rückführung der Zahle 31 auf 31 - 27 = 4. Im 2. und 3. Block ist die Rückführung ebenfalls erfolgt. So ist 21 + 9 = 30; 30 - 27 = 3 und 26 + 9 = 35; 35 - 27 = 8. Die Differenzen zwischen den Blöcken sind jedoch nicht einheitlich. Sie sind einmal 8 (von 4 zu 12) und einmal 14 (von 3 zu 17). Auch das ist logisch und hat Mag bei der Bildung von Domino- und Mosaikquadraten beschrieben. Das ist auch der Grund, weshalb diese äußeren Quadrate keine magischen, sondern nur halbmagische Quadrate sein können. Diese gewonnenen Erkenntnisse sind zwar interessant, sind aber nicht der Schlüssel zur Bildung magischer Würfel, weshalb diese auch nicht die Leistungen des Schöpfers dieses magischen Würfels schmälern können.
Mag nutzten jedoch diese Erkenntnisse zur Bildung seines magischen Primzahlen-Würfels. Leider ist es Mag nicht gelungen diesen als teilmagischen Würfel zu gestalten, sondern lediglich als halbmagischen. Die magische Summe entspricht dafür aber der Primzahl 17077. Alle 27 waagerechten und senkrechten Primzahlenreihen haben die magische Summe von 17077. Alle 3 roten Quadrate, die die mittlere Primzahl 4339 als mittlere Zahl haben, besitzen eine Diagonale mit der magischen Summe. Die zweite Diagonale leider nicht. Bei den 6 äußeren Quadraten (grün und blau) hat keine der beiden Diagonalen die magische Summe.
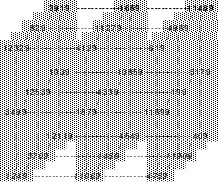
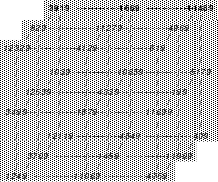
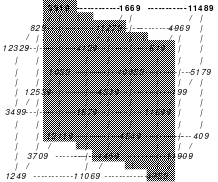
Und wie bei dem Würfel aus natürlichen Zahlen ist keines der 6 Quadrate, die durch Diagonalschnitte entstehen magisch, sondern nur teilmagisch. Diese haben jeweils 4 Zahlenreihen (3 Spalten und 1 Zeile bzw. 3 Zeilen und 1 Spalte) mit der magischen Summe 17077.
Bei 4 dieser Quadrate haben auch beide Diagonalen die magische Summe. Bei den anderen 2 Quadraten leider nur eine Diagonale. Das gelb gekennzeichnete Quadrat ist eins davon. Hier ist die Summe der Diagonale von 3919 über 4339 nach 4759 nur 13017 groß. Da diese auch eine Würfeldiagonale ist, haben nur 3 der 4 Würfeldiagonale die magische Summe.
Wie Mag den magischen Primzahlen-Würfel aufgebaut hat und warum ihm nur ein halbmagischer Würfel gelungen ist, beschreibt er nachfolgend.
Mag hatte festgestellt, dass bei dem magischen Würfel aus natürlichen Zahlen 3 mal 9 Zahlen zum Einsatz gekommen waren. Er ging nun davon aus, dass bei Einsatz von 3 arithmetischen Primzahlenreihen mit je 9 Primzahlen an Stelle der Zahlen von 1 bis 27 ein magischer Primzahlenwürfel entstehen müsste. Im Abschnitt ´Primzahlenreihen´ hatte Mag unter ´Hypothese´ die Bildung von Primzahlenreihen mit bis zu 10 Gliedern je Reihe erläutert. Als Differenz zwischen den Gliedern hatte Mag mit 210 eingesetzt. Er benötigte für den Würfel lediglich 3 Reihen mit je 9 Primzahlen. Er hatte bei der Auswertung aller Primzahlen bis 50000 lediglich 3 derartige Reihen gefunden. Um aber die mittleren (roten) Quadrate als magische zu gestalten müsste die Differenz zwischen den 3 Reihen gleichgroß sein. Das war nicht der Fall. Mag schätzte ein, dass es bei der geringen Ausbeute von nur 3 Reihen aus den Primzahlen bis 50000 überhaupt nicht möglich sein wird, 3 solcher Reihen, selbst bei Einsatz aller Primzahlen bis zu 1 Mio., zu finden. Aber die Bildung eines halbmagischen Primzahlenwürfels müsste so erreichbar sein. Mag setzte die gefundenen 3 Reihen mit mindestens 9 Gliedern für die Bildung des magischen Würfels ein. Es war Zufall, dass die mittleren Zahlen (die 5ten) als Summe eine Primzahl ergaben. Das war mit den nachfolgend aufgelisteten Primzahlenreihen möglich (1039 + 4339 + 11699 = 17077 - eine Primzahl).
Mag nummerierte die 3 Reihen mit den Zahlen von 1 bis 9, 10 bis 18 und 19 bis 27. Die zugehörigen Primzahlen setzte er einfach entsprechen der Zahlen in das Quadrat der 3. Ordnung aus natürlichen Zahlen von 1 bis 27 ein und der dargestellte halbmagische Primzahlenwürfel war geschaffen.
Im Nachhinein sieht das Ganze rechts einfach aus. Aber mal ehrlich, wären Sie darauf gekommen? Hätten Sie an den Einsatz von 3 arithmetischen Primzahlenreihen mit je 9 Gliedern in den magischen Würfel der Ordnung 3 mit natürlichen Zahlen gedacht und hätten Sie diese auch ohne Mag´s Hilfe gefunden?
9.7. Zwischendurch
In den Einführungen zum Hexen 1x1 hatte Mag die Empfehlung gegeben, zwischen den einzelnen Darbietungen mit magischen Quadraten andere Rechenkunststücke zur Auflockerung einzubinden.
Nachfolgend 3 mögliche Darbietungen, wovon “Kleiner Spaß” als heitere einzustufen ist.
6 aus 3
Auch wenn das Geheimnis dieses Experiments relativ leicht erkannt werden kann, führt Mag es immer wieder gern vor. Mag hat dieses Experiment noch nie von einem Rechenkünstler vorgeführt gesehen, auch wurde es nach seiner Kenntnis noch nicht in der Literatur beschrieben. Das liegt daran, dass Mag dieses Experiment aus einem völlig anderen entwickelt hat. Doch nun zum Geschehen.
Mag bittet einen Gast an die Tafel. Diesen bittet er, eine 3-stellige Zahl mit unterschiedlichen Ziffern oben an die Tafel zu schreiben. Es können alle Ziffern außer Null eingesetzt werden. Ist der Gast der Bitte nachgekommen, geht Mag zur Tafel und schreibt eine größere Zahl an diese. Danach bittet Mag den Gast aus den 3 eingesetzten Ziffern durch Kombination derselben (genauer Permutation) alle 6 möglichen 3-stelligen Zahlen untereinander an die Tafel zu schreiben und anschließend zu addieren. Das Ergebnis stimmt mit der von Mag vorher an die Tafel geschriebenen Zahl überein!
Da Mag seine Aufgabe mit dem Anschreiben des Ergebnisses erledigt hat, kann er die Zahlenbildung und Addition des Gastes kontrollieren, damit dieser keinen Fehler bei der Bildung der 6 möglichen Zahlen und bei der Berechnung deren Summe macht.
Die Lösung ist denkbar einfach!
Im Beispiel hat der Gast die Zahl 469 gewählt. Aus den Ziffern 4, 6 und 9 können weitere fünf 3-stellige Zahlen gebildet werden. Die insgesamt 6 möglichen Zahlen sind 469, 496, 649, 694, 946 und 964.
Analysiert man diese 6 Zahlen, so kann man feststellen, dass jede der 3 Ziffern 2-mal als Hunderter, 2-mal als Zehner und 2-mal als Einer zu finden sind.
Schon während des Gasts die erste Zahl an die Tafel schreibt, bildet Mag die Quersumme und wenn er zur Tafel geht, multipliziert er diese Summe mit 2 und dann mit 111.
Das Ergebnis ist damit gefunden, welches Mag an die Tafel schreibt.
Die Rechenoperationen, besonders das Multiplizieren mit 111, sind nicht so kompliziert wie es scheint.
Verkürzt dargestellt rechnet man folgendermaßen (a, b und c sind die Ziffern):
a + b + c = QS1 (Quersumme 1) x 2 = AZ (Ausgangszahl) x 111 = E (Ergebnis).
(Für die weiteren Berechnungen wird noch der Wert QS2 als Quersumme der
Ausgangszahl (AZ) gebildet.)
Im Beispiel folglich: 4 + 6 + 9 = 19 x 2 = 38 x 111 = 4218
Die Multiplikation der Ausgangszahl mit 111 ist dabei denkbar einfach.
Das Ergebnis kann nach den vorn genannten leichten Berechnungen regelrecht konstruiert werden. Die Konstruktion erfolgt dabei nach 2 Regeln.
Dabei gilt: Ist die Quersumme von AZ (QS2) 1-stellig, so gilt Regel 1
Ist die Quersumme von AZ (QS2) 2-stellig, so Regel 2
Regel 1
Ist die Quersumme der Ausgangszahl (QS2) einstellig so gilt diese Regel. Die Erläuterung erfolgt anhand der Ausgangszahl von 24:
Zwischen die beiden Ziffern von AZ werden gedanklich 2 Nullen eingefügt. Man erhält 2004.
Die 2 Nullen werden ersetzt durch die Quersumme der Ausgangszahl (QS2). Man erhält 2664 und hat damit das Ergebnis (E) gefunden!
Regel 2
Die Regel 2 kommt seltener, etwa in nur 20 % der Fälle vor. Diese Regel gilt, wenn die Quersumme der Ausgangszahl 2-stellig ist.
Als Beispiel soll die vom Zuschauer gewählte Zahl 649 sein. Daraus ergeben sich folgende Werte:
QS1 = 6 + 4 + 9 = 19; AZ = 19 x 2 = 38; QS2 = 3 + 8 = 11
Hier wird das Ergebnis anfangs wie bei der Regel 1 konstruiert:
Es werden zwischen die Ziffern von AZ gedanklich 2 Nullen eingefügt. Das ist 3008.
Die Nullen werden durch die letzte Ziffer von QS2 ersetzt. Aus 3008 wird 3118.
Zum Schluss werden die ersten beiden Ziffern um 1, das ist die erste Ziffer von QS2 erhöht. (QS2 ist niemals größer 1) Aus 3118 wird 4218 das Ergebnis!
Es kann festgestellt werden, dass es sich bei diesem Experiment um eine einfache und leichte Lösung handelt. Das sollte aber nicht dazu verleiten, dieses Experiment mehrmals zu wiederholen. Warum, das entnehmen Sie bitte den folgenden Hinweisen.
Hinweise.
Obwohl der Gast die Wahl zwischen 864 Zahlen hat (987 - 123 = 864), sind nur 19 unterschiedliche Lösungen möglich. Das Ergebnis wird aus den Ausgangszahlen gebildet die als Reihe mit einer Differenz von 2 dargestellt werden können (12, 14, 16, 18, .... 46, 48). Zum Beispiel haben die Zahlen 914, 527, 347, 176, ... und viele weitere, die gleiche Ausgangszahl von 28. Wegen der nur 19 möglichen Ergebnisse sollte auf eine Wiederholung verzichtet werden.
Auch die Tatsache, dass die beiden mittleren Ziffern die Summe der beiden äußeren ist, rät dazu.
Eine Ausnahme ist eine Zahl, deren Ausgangszahl 2-stellig wird. Hier bietet sich eine Wiederholung an. Denn hier werden die Ziffern unterschiedlich sein.
Bei einer Wiederholung sollten Sie sich die bisherige QS1 (a + b + c) gut merken. Hat ein Gast Ziffern gewählt, die im Ergebnis eine schon mal da gewesene Quersumme ergeben, so bitten Sie den Gast eine Ziffer auszutauschen.
Sollte ein Gast entgegen ihrer Bitte eine Zahl mit einer Null bilden, so prüfen Sie, ob QS1 > 5 wird. Ist das nicht der Fall, machen Sie auf den Fehler aufmerksam und bitten um Änderung. Denn wird QS1 < 6, so wird das Ergebnis, nur aus gleichen Ziffern bestehen.
Beispiel: Zahl 301; QS1 = 4; AZ = 8; QS2 = 8; Ergebnis = 888
Zahl 410; QS1 = 5; AZ = 10; QS2 = 1; Ergebnis = 1110
Wird QS1 jedoch > 5, so ermitteln Sie einfach das Ergebnis wie beschrieben.
Beispiel: Zahl 501; QS1 = 6; AZ = 12; Ergebnis 1332.
Dieses Problem tritt jedoch auch bei der Bildung von Zahlen aus unterschiedlichen Ziffern auf und zwar bei bis zu rd. 16%. Nämlich dann, wenn QS1 = 10; 15 oder 20 groß ist.
Beispiele: Zahl 523; QS1 = 10; AZ = 20; QS2 = 2; Ergebnis = 2220
Zahl 834; QS1 = 15; AZ = 30; QS2 = 3; Ergebnis = 3330
Zahl 758; QS1 = 20; AZ = 40; QS2 = 4; Ergebnis = 4440
Sie können den Gast bitten eine Ziffer zu ändern, Sie können aber auch die Aufgabe lösen. Im letzteren Fall ist eine Wiederholung mit einem anderen Gast und anderer Zahl zwingend, denn Sie müssen beweisen, dass dieses sonderbare Ergebnis ein reiner Zufall war.
Ein weiteres Problem kann auftreten, wenn ein Gast versehentlich oder absichtlich eine Ziffer doppelt einsetzt. In diesem Fall prüfen Sie, ob QS1 > 10 ist. Wenn das nicht zutrifft, so bitten Sie um entsprechende Änderung. Ist QS1 > 10, so sehen Sie darüber hinweg und bilden das Ergebnis.
Weil in diesem Fall nur 3 mögliche Zahlen gebildet werden können, wird QS1 = AZ gesetzt. Auch hierzu Beispiele:
Zahl 313; mögliche Zahlen: 313; 331 und 133; QS1 = AZ = 7; Ergebnis 777
Zahl 262; mögliche Zahlen: 262; 226 und 622; QS1 = AZ = 10; Ergebnis 1110
Zahl 474; mögliche Zahlen: 474; 447 und 744; QS1 = AZ = 15; Ergebnis 1665
Durchstochenes
Mangels einer mit großen Papierbogen bestückten Infotafel hat Mag einige große Bogen Papier (notfalls Packpapier) mittels Sticker an einer ebenen Fläche befestigt. Auf dem oberen ist ein akkurat gezeichnetes 5er Quadrat aufgezeichnet.
Er lässt sich eine 3-stellige Zahl kleiner 200 nennen. Die genannte 172 schreibt er in die Mitte des Quadrates. Anschließend bildet er ein magisches Quadrat mit der magischen Summe 860. Alles wie im kleinen Hexen 1x1 beschrieben, mit der Schlüsselzahl 7, weil 7*9 kleiner 100 ist.
Nachdem das Staunen und evtl. auch der Beifall abgeklungen sind, nimmt er den Bogen ab und faltet diesen um die waagerechte und weiter um die senkrechte Achse des Quadrates (Siehe blaue Linien) und zwar so, dass die Zahlen außen sichtbar sind. Egal wie gefaltet wurde, auf der Ober- und Unterseite des Paketes sind jeweils 4 vollständige Zahlen zu sehen.
Einem Zuschauer wird ein spitzer Gegenstand (Brieföffner, Schaschlikspieß, Ahle oder notfalls auch eine große Nadel) übergeben, mit der Bitte, das gefaltete Paket an einer frei gewählten Zahl zu durchstechen. (Das Papier sollte deshalb nicht zu dick und nicht zu fest sein.)
Ist das erfolgt, lässt sich Mag die Zahl nennen, durch die das Paket durchstochen wurde. Es wurde 207 genannt. Sofort schreibt Mag auf die Interimstafel die Zahl 688.
Den Helfer bittet Mag alle 4 durchstochenen Zahlen aufzuschreiben und deren Summe zu bilden. Die Summe ist 688, wie sie Mag vorher angeschrieben hat.
Mag war es gelungen, von der genannten Zahl ausgehend, die anderen 3 Zahlen zu ermitteln und alle 4 zu addieren und das innerhalb eines sehr kurzen Momentes.
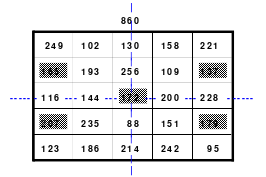
Wie war das möglich?
Nun, Mag hat gerechnet, aber nicht so kompliziert und auch nicht in einem sehr kurzen Moment. Zum Rechnen hatte er viel Zeit. Denn während sich die Zuschauer und die Jury mit dem Ergebnis des gebildeten Quadrates befassten, hat Mag die Vorgabe 172 verdoppelt und erhielt so 172*2=344. Das ist die Duosumme. Danach dieser Methode 2 Duos durchstochen werden, hat er 344 ebenfalls verdoppelt und 344*2=688 erhalten, die er sich gemerkt hat, um sie zum gegebenen Zeitpunkt an die Tafel zu schreiben oder auch nur zu nennen.
Auch bietet sich die einfache Form der Multiplikation einer mehrstelligen Zahl mit einer einstelligen an. Denn 2*2 ist 4, folglich ist die Summe der 4 durchstochenen Zahlen das 4-fache der Vorgabe.
Für die Vorgabe 172 wäre das:
172*4 --> 1*4=4 --> Null anhängen =40+7*4=40+28=68 --> Null anhängen =680+2*4=688, das Ergebnis.
Im Beispiel sind die durchstochenen Zahlen die Duos 207/137 und 165/179. Die durchstochenen Zahlen befinden sich stets symmetrisch zum Mittelpunkt, der Zelle 13, wie auch die 2 Zahlen aller anderen Duos.
Es ist also völlig egal durch welche Zahl gestochen wird, das Ergebnis ist 688. Deshalb ist auch eine Wiederholung mit dem gleichen Quadrat nicht möglich.
Dass sich Mag die Zahl, die sichtbar durchstochen wurde, nennen lässt, dient der Verschleierung der wirklichen Handlungen und täuscht vor, dass diese zur Ermittlung der Summe erforderlich ist. Mag konnte zum Schein erst nach der Nennung der Zahl mit seinen Ermittlungen und der Summenberechnung beginnen.
Nicht egal ist hingegen das Quadrat. Es muss bestimmte Bedingungen erfüllen. Diese werden vor allem von den Springerquadraten erbracht. Bei diesen sind die Duozahlen jedes Duos symmetrisch zur mittleren Zelle angeordnet. Die Vorgabe muss deshalb auch in die mittlere Zelle eingesetzt werden. Diese Ordnung darf nicht aufgehoben werden, z. B. durch die Einordnung eines Restes, oder durch unterschiedliche Übergänge von Block zu Block. Alle Zellen müssen gleichbehandelt werden, was beim obigen Quadrat durch die einheitliche Multiplikation aller Zellenzahlen mit der Schlüsselzahl 7 erfolgte.
Auch ein zusätzlicher Summand wäre möglich. Er müsste aber ebenfalls allen Zellen zugeschlagen werden.
Diese Bedingungen kann auch das Springerquadrat der 7. Ordnung erfüllen. Dabei werden auf der Ober- und Unterseite der Faltung sogar jeweils 9 Zahlen zum Durchstechen angeboten.
Kleiner Spaß
Zum Abschluss seiner Darbietung erlaubt sich Mag einen kleinen Spaß, der die evtl. vorhandene Anspannung der Zuschauer auflockern soll.
Mag erklärt, dass Mathematik eine recht einfache Sache ist, was er an einem Beispiel beweisen möchte.
Er schreibt an die Tafel die Rechenaufgabe 21: 3 und beginnt mit der Lösung, indem er erklärt:
Natürlich muss das Ganze mit einem heiteren Lächeln vorgeführt werden.
Viel Spaß mit dem kleinen Spaß!
Nebenbei gesagt, der Spaß ist auch mit den Formeln 12:3=13; 24:6=13 und 42:6=16 möglich.
Welche der genannten Varianten Sie nutzen, ist ihnen überlassen. Sicherlich finden Sie auch weitere.
ENDE